RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
Other Exercises
- RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1
- RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
- RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
- RD Sharma Class 10 Solutions Chapter 8 Circles MCQS
Question 1.
If PT is a tangent at T to a circle whose centre is O and OP = 17 cm, OT = 8 cm. Find the length of the tangent segment PT.
Solution:
PT is the tangent to the circle with centre O, at T
Radius OT = 8 cm, OP = 17 cm
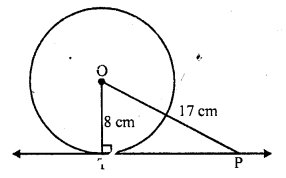
PT is the tangent segment
Now in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
=> (17)² = (8)² + PT²
=> 289 = 64 + PT²
=> PT² = 289 – 64 = 225 = (15)²
PT = 15 cm
Question 2.
Find the length of a tangent drawn to a circle with radius 5 cm, from a point 13 cm from the centre of the circle.
Solution:
From a point P outside the circle with centre O, PT is the tangent to the circle and radius
OT = 5 cm, OP = 15 cm
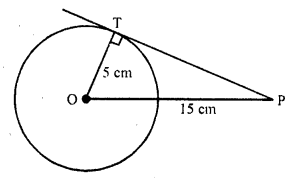
OT ⊥ PT
Now in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
(13)² = (5)² + PT²
=> 169 = 25 + PT²
=> PT² = 169 – 25 = 144 = (12)²
PT = 12 cm
Question 3.
A point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
Solution:
From a point P outside the circle of centre 0 and radius OT, PT is the tangent to the circle
OP = 26 cm, PT = 10 cm
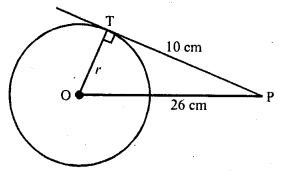
Now in right ∆OPT
Let r be the radius
OP² = OT² + PT² (Pythagoras Theorem)
=> (26)² = r² + (10)²
=> 676 = r² + 100
=> 676 – 100 = r²
=> r² = 576 = (24)²
r = 24
Hence radius of the circle = 24 cm
Question 4.
If from any point on the common chord of two intersecting circles, tangents be drawn to the circles, prove that they are equal.
Solution:
Given : QR is the common chord of two circles intersecting each other at Q and R
P is a point on RQ when produced From PT and RS are the tangents drawn to tire circles with centres O and C respectively
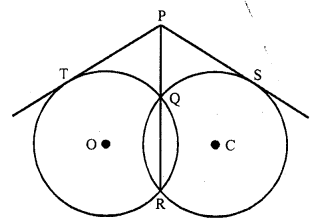
To prove : PT = PS
Proof: PT is the tangent and PQR is the secant to the circle with centre O
PT² = PQ x PR ….(i)
Similarly PS is the tangent and PQR is the secant to the circle with centre C
PS² = PQ x PR ….(ii)
From (i) and (ii)
PT² = PS²
PT = PS
Hence proved.
Question 5.
If the sides of a quadrilateral touch a circle, prove that the sum of a pair of opposite sides is equal to the sum of the other pair.
Solution:
Given : The sides of a quadrilateral ABCD touch the circle at P, Q, R and S respectively
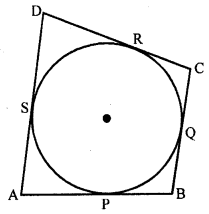
To prove : AB + CD = AP + BC
Proof : AP and AS are the tangents to the circle from A
AP = AS ….(i)
Similarly BP = BQ ……(ii)
CR = CQ ….(iii)
and DR = DS ….(iv)
Adding, we get
AP + BP + CR + DR = AS + BQ + CQ + DS
=> (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
=> AB + CD = AD + BC
Hence proved.
Question 6.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle. [NCERT Exemplar]
Solution:
Let C1 and C2 be the two circles having same centre O. AC is a chord which touches the C1 at point D
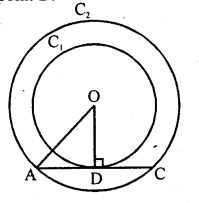
Join OD.
Also, OD ⊥ AC
AD = DC = 4 cm
[perpendicular line OD bisects the chord]
In right angled ∆AOD,
OA² = AD² + DO²
[by Pythagoras theorem, i.e.,
(hypotenuse)² = (base)² + (perpendicular)²]
=> DO² = 5² – 4² = 25 – 16 = 9
=> DO = 3 cm
Radius of the inner circle OD = 3 cm
Question 7.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ. [NCERT Exemplar]
Solution:
Given : Chord PQ is parallel tangent at R.
To prove : R bisects the arc PRQ.
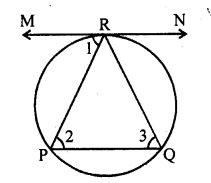
Proof: ∠1 = ∠2 [alternate interior angles]
∠1 = ∠3
[angle between tangent and chord is equal to angle made by chord in alternate segment]
∠2 = ∠3
=> PR = QR
[sides opposite to equal angles are equal]
=> PR = QR
So, R bisects PQ.
Question 8.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A. [NCERT Exemplar]
Solution:
Given, AB is a diameter of the circle.
A tangent is drawn from point A.
Draw a chord CD parallel to the tangent MAN.
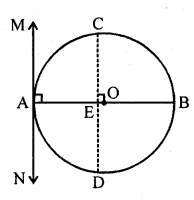
So, CD is a chord of the circle and OA is a radius of the circle.
∠MAO = 90°
[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
∠CEO = ∠MAO [corresponding angles]
∠CEO = 90°
Thus, OE bisects CD
[perpendicular from centre of circle to chord bisects the chord]
Similarly, the diameter AB bisects all. Chord which are parallel to the tangent at the point A.
Question 9.
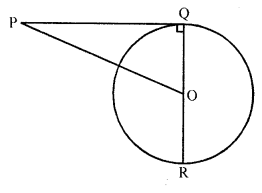
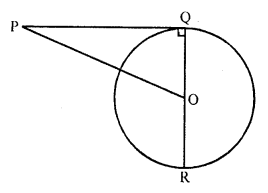
If AB, AC, PQ are the tangents in the figure, and AB = 5 cm, find the perimeter of ∆APQ.
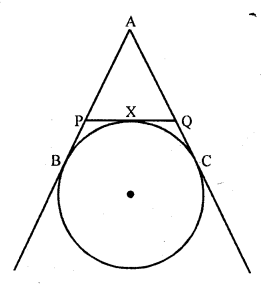
Solution:
Given : AB, AC and PQ are the tangents to the circle as shown in the figure above and AB = 5 cm
To find : The perimeter of ∆APQ
Proof: PB and PX are the tangents to the circle
PB = PX
Similarly QC and QX are the tangents from
QC = QX
and AB and AC are the tangents from A
AB = AC
Now perimeter of ∆APQ
= AP + PQ + AQ
= AP + PX + QX + AQ
= AP + PB + QC + AQ { PB = PX and QC = QX}
= AB + AC
= AB + AB (AB=AC)
= 2 AB = 2 x 5 = 10 cm
Question 10.
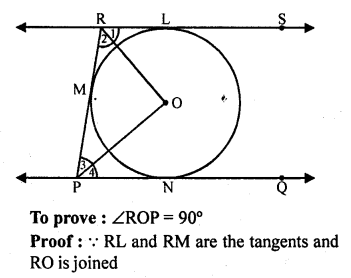
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
Solution:
Given : PQ and RS are parallel tangents of a circle
RMP is the intercept of the tangent between PQ and RS
RO and PQ are joined

Question 11.
In the figure, PQ is tangent at a point R of the circle with centre O. If ∠TRQ = 30°, find m ∠PRS
Solution:
In the figure,
PRQ is tangent to the circle with centre O at R
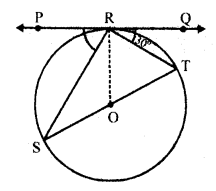
RT and RS are joined such that ∠TRQ = 30°
Let ∠PRS = x°
Now ∠SRX = 90° (angle in a semicircle)
But ∠TRQ + ∠SRT + ∠PRS = 180° (Angles of a line)
=> 30° + 90° + x° = 180°
=> 120° + x° = 180°
=> x° = 180° – 120° = 60°
∠PRS = 60°
Question 12.
If PA and PB are tangents from an outside point P, such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
Solution:
PA and PB are the tangents from a point PQ outside the circle with centre O
PA = 10 cm and ∠APB = 60°
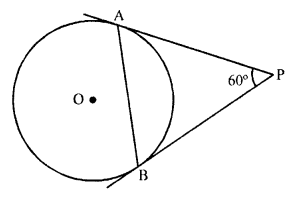
Tangents drawn from a point outside the circle are equal
PA = PB = 10 cm ∠PAB = ∠PBA
(Angles opposite to equal sides)
But in ∆APB,
∠APB + ∠PAB + ∠PBA = 180° (Angles of a triangle)
=> 60° + ∠PAB + ∠PAB = 180°
=> 2 ∠PAB = 180° – 60° = 120°
∠PAB = 60°
∠PBA = ∠PAB = 60°
PA = PB = AB = 10 cm
Hence length of chord AB = 10 cm
Question 13.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC. [NCERT Exemplar]
Solution:
Let O be the centre of the given circle. Suppose, the tangent at P meets BC at Q.
Join BP.
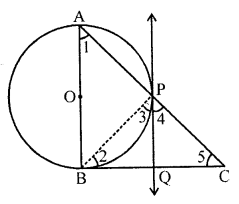
To prove : BQ = QC
[angles in alternate segment]
Proof : ∠ABC = 90°
[tangent at any point of circle is perpendicular to radius through the point of contact]
In ∆ABC, ∠1 + ∠5 = 90°
[angle sum property, ∠ABC = 90°]
∠3 = ∠1
[angle between tangent and the chord equals angle made by the chord in alternate segment]
∠3 + ∠5 = 90° ……..(i)
Also, ∠APB = 90° [angle in semi-circle]
∠3 + ∠4 = 90° …….(ii)
[∠APB + ∠BPC = 180°, linear pair]
From Eqs. (i) and (ii), we get
∠3 + ∠5 = ∠3 + ∠4
∠5 = ∠4
=> PQ = QC
[sides opposite to equal angles are equal]
Also, QP = QB
[tangents drawn from an internal point to a circle are equal]
=> QB = QC
Hence proved.
Question 14.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If CD is the tangent to the circle at a point E and PA = 14 cm, find the perimeter of ∆PCD.
Solution:
PA and PB are the tangents drawn from a point P out side the circle with centre O
CD is another tangents to the circle at point E which intersects PA and PB at C and D respectively
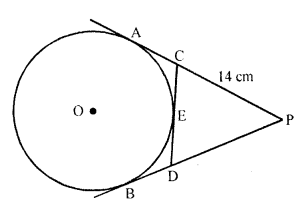
PA = 14 cm
PA and PB are the tangents to the circle from P
PA = PB = 14 cm
Now CA and CE are the tangents from C
CA = CE ….(i)
Similarly DB and DE are the tangents from D
DB = DE ….(ii)
Now perimeter of ∆PCD
= PC + PD + CD
= PC + PD + CE + DE
= PC + CE + PD + DE
= PC + CA + PD = DB {From (i) and (ii)}
= PA + PB
= 14 + 14
= 28 cm
Question 15.
In the figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle. [CBSE 2002]
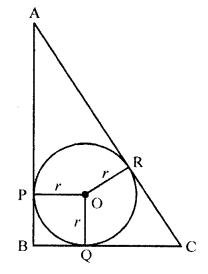
Solution:
In right ∆ABC, ∠B = 90°
BC = 6 cm, AB = 8 cm
Let r be the radius of incircle whose centre is O and touches the sides A B, BC and CA at P, Q and R respectively
AP and AR are the tangents to the circle AP = AR
Similarly CR = CQ and BQ = BP
OP and OQ are radii of the circle
OP ⊥ AB and OQ ⊥ BC and ∠B = 90° (given)
BPOQ is a square
BP = BQ = r
AR = AP = AB – BD = 8 – r
and CR = CQ = BC – BQ = 6 – r
But AC² = AB² + BC² (Pythagoras Theorem)
= (8)² + (6)² = 64 + 36 = 100 = (10)²
AC = 10 cm
=> AR + CR = 10
=> 8 – r + 6 – r = 10
=> 14 – 2r = 10
=> 2r = 14 – 10 = 4
=> r = 2
Radius of the incircle = 2 cm
Question 16.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc. [NCERT Exemplar]
Solution:
Let mid-point of an arc AMB be M and TMT’ be the tangent to the circle.
Join AB, AM and MB.
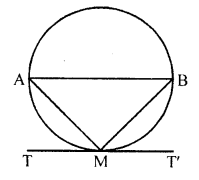
Since, arc AM = arc MB
=> Chord AM = Chord MB
In ∆AMB, AM = MB
=> ∠MAB = ∠MBA ……(i)
[equal sides corresponding to the equal angle]
Since, TMT’ is a tangent line.
∠AMT = ∠MBA
[angle in alternate segment are equal]
∠AMT = ∠MAB [from Eq. (i)]
But ∠AMT and ∠MAB are alternate angles, which is possible only when AB || TMT’
Hence, the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Hence proved
Question 17.
From a point P, two tangents PA and PB are drawn to a circle with centre O. If OP = diameter of the circle show that ∆APB is equilateral.
Solution:
Given : From a point P outside the circle with centre O, PA and PB are the tangerts to the circle such that OP is diameter.
AB is joined.
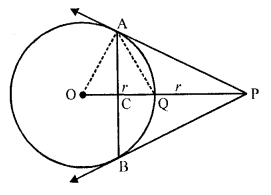
To prove: APB is an equilateral triangle
Const : Join OP, AQ, OA
Proof : OP = 2r
=> OQ + QP = 2r
=> OQ = QP = r (OQ = r)
Now in right ∆OAP,
OP is its hypotenuse and Q is its mid point
OA = AQ = OQ
(mid-point of hypotenuse of a right triangle is equidistances from its vertices)
∆OAQ is equilateral triangle ∠AOQ = 60°
Now in right ∆OAP,
∠APO = 90° – 60° = 30°
=> ∠APB = 2 ∠APO = 2 x 30° = 60°
But PA = PB (Tangents from P to the circle)
=> ∠PAB = ∠PBA = 60°
Hence ∆APB is an equilateral triangle.
Question 18.
Two tangents segments PA and PB are drawn to a circle with centre O such that ∠APB = 120°. Prove that OP = 2 AP. [CBSE 2014]
Solution:
Given : From a point P. Out side the circle with centre O, PA and PB are tangerts drawn and ∠APB = 120°
OP is joined To prove : OP = 2 AP
Const: Take mid point M of OP and join AM, join also OA and OB.
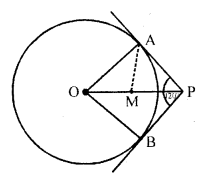
Proof : In right ∆OAP,
∠OPA = \(\frac { 1 }{ 2 }\) ∠APB = \(\frac { 1 }{ 2 }\) x 120° = 60°
∠AOP = 90° – 60° = 30°
M is mid point of hypotenuse OP of ∆OAP
MO = MA = MP
∠OAM = ∠AOM = 30° and ∠PAM = 90° – 30° = 60°
∆AMP is an equilateral triangle
MA = MP = AP
But M is mid point of OP
OP = 2 MP = 2 AP
Hence proved.
Question 19.
If ∆ABC is isosceles with AB = AC and C (0, r) is the incircle of the ∆ABC touching BC at L. Prove that L bisects BC.
Solution:
Given: In ∆ABC, AB = AC and a circle with centre O and radius r touches the side BC of ∆ABC at L.
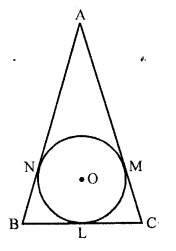
To prove : L is mid point of BC.
Proof : AM and AN are the tangents to the circle from A
AM = AN
But AB = AC (given)
AB – AN = AC – AM
BN = CM
Now BL and BN are the tangents from B
BL = BN
Similarly CL and CM are tangents
CL = CM
But BM = CM (proved)
BL = CL
L is mid point of BC.
Question 20.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects AB at a point D. Prove that BC = BD. [NCERT Exemplar]
Solution:
To prove, BC = BD
Join BC and OC.
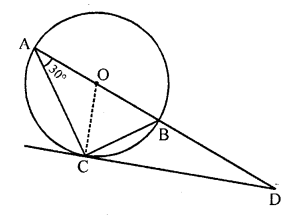
Given, ∠BAC = 30°
=> ∠BCD = 30°
[angle between tangent and chord is equal to angle made by chord in the alternate segment]
∠ACD = ∠ACO + ∠OCD
∠ACD = 30° + 90° = 120°
[OC ⊥ CD and OA = OC = radius => ∠OAC = ∠OCA = 30°]
In ∆ACD,
∠CAD + ∠ACD + ∠ADC = 180°
[since, sum of all interior angles of a triangle is 180°]
=> 30° + 120° + ∠ADC = 180°
=> ∠ADC = 180° – (30° + 120°) = 30°
Now, in ∆BCD,
∠BCD = ∠BDC = 30°
=> BC = BD
[since, sides opposite to equal angles are equal]
Question 21.
In the figure, a circle touches all the four sides of a quadrilateral ABCD with AB = 6 cm, BC = 7 cm, and CD = 4 cm. Find AD. [CBSE 2002]
Solution:
A circle touches the sides AB, BC, CD and DA of a quadrilateral ABCD at P, Q, R and S respectively.
AB = 6 cm, BC = 7 cm, CD = 4cm
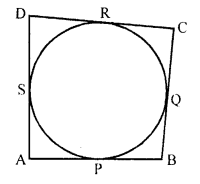
Let AD = x
AP and AS are the tangents to the circle
AP = AS
Similarly,
BP = BQ
CQ = CR
and OR = DS
AB + CD = AD + BC
=> 6 + 4 = 7 + x
=> 10 = 7 + x
=>x = 10 – 7 = 3
AD = 3 cm
Question 22.
Prove that the perpendicular at the point contact to the tangent to a circle passes through the centre of the circle.
Solution:
Given : TS is a tangent to the circle with centre O at P, OP is joined
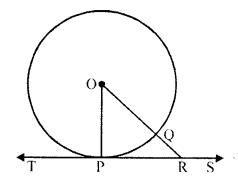
To prove : OP is perpendicular to TS which passes through the centre of the circle
Construction : Draw a line OR which intersect the circle at Q and meets the tangent TS at R
Proof: OP = OQ
(radii of the same circle) and OQ < OR => OP < OR
Similarly we can prove that OP is less than all lines which can be drawn from O to TS
OP is the shortest
OP is perpendicular to TS
Perpendicular through P, will pass through the centre of the circle
Hence proved.
Question 23.
Two circles touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ = TR.
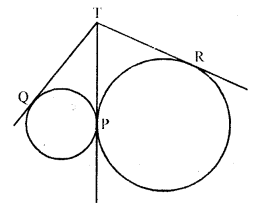
Solution:
Given : Two circles with centres O and C touch each other externally at P. PT is its common tangent
From a point T on PT, TR and TQ are the tangents drawn to the circles
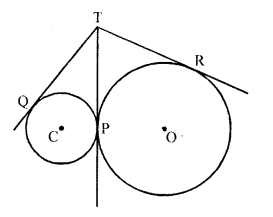
To prove : TQ = TR
Proof : From T, TR and TP are two tangents to the circle with centre O
TR = TP ….(i)
Similarly, from T,
TQ and TP are two tangents to the circle with centre C
TQ = TP ….(ii)
From (i) and (ii)
TQ = TR
Hence proved.
Question 24.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC. [NCERT Exemplar]
Solution:
Given : Two tangents are drawn from an external point A to the circle with centre O, Tangent BC is drawn at a point R, radius of circle equals to 5 cm.
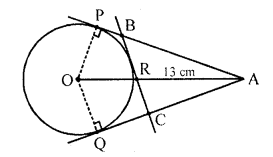
To find : Perimeter of ∆ABC.
Proof : ∠OPA = 90°
[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
OA² = OP² + PA² [by Pythagoras Theorem]
(13)² = 5² + PA²
=> PA² = 144 = 12²
=> PA = 12 cm
Now, perimeter of ∆ABC = AB + BC + CA = (AB + BR) + (RC + CA)
= AB + BP + CQ + CA [BR = BP, RC = CQ tangents from internal point to a circle are equal]
= AP + AQ = 2AP = 2 x (12) = 24 cm
[AP = AQ tangent from internal point to a circle are equal]
Hence, the perimeter of ∆ABC = 24 cm.
Question 25.
In the figure, a circle is inscribed in a quadrilateral ABCD in which ∠B = 90°. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the radius r of the circle.
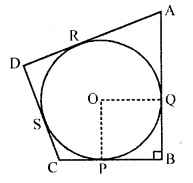
Solution:
In the figure, O is the centre of the circle inscribed in a quadrilateral ABCD and ∠B = 90°
AD = 23 cm, AB = 29 cm, DS = 5 cm
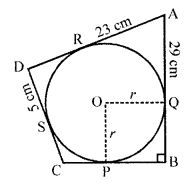
OP = OQ (radii of the same circle)
AB and BC are tangents to the circle and OP and OQ are radii
OP ⊥ BC and OQ ⊥ AB
∠OPB = ∠OQB = 90°
PBQO is a square
DS and DR are tangents to the circle
DR = DS = 5 cm
AR = AD – DR = 23 – 5 = 18 cm
AR and AQ are the tangents to the circle
AQ = AR = 18 cm But AB = 29 cm
BQ = AB – AQ = 29 – 18 = 11 cm
Side of square PBQO is 11 cm
OP = 11 cm
Hence radius of the circle = 11 cm
Question 26.
In the figure, there are two concentric circles with centre O of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP =12 cm, find the length of BP. [CBSE 2010]
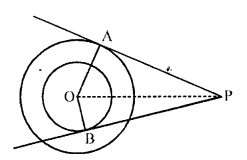
Solution:
Two concentric circles with centre O with radii 5 cm and 3 cm respectively from a
point P, PA and BP are tangents drawn to there circles
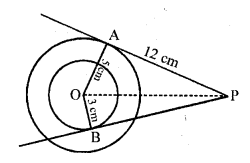
AP = 12 cm
To find BP
In right ∆OAP,
OP² = OA² + AP² (Pythagoras Theorem)
= (5)² + (12)² = 25 + 144
= 169 = (13)²
OP = 13 cm
Now in right ∆OBP,
OP² = OB² + BP²
=> (13)² = (3)² + BP²
=> 169 = 9 + BP²
=> BP² = 169 – 9 = 160 = 16 x 10
BP = √(16 x 10) = 4√10 cm
Question 27.
In the figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA. [CBSE 2010]
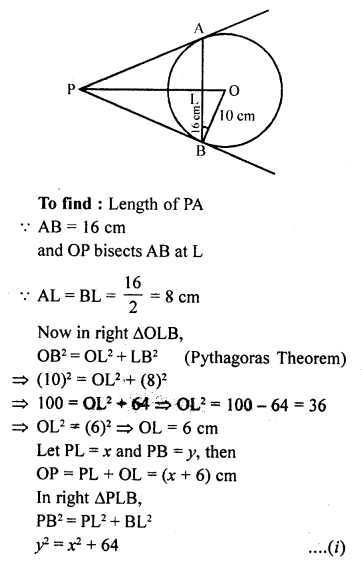
Solution:
In the figure, AB is the chord of the circle with centre O and radius 10 cm.
Two tangents from P are drawn to the circle touching it at A and B respectively
AB is joined with intersects OP at L

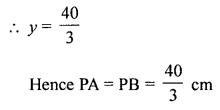
Question 28.
In the figure, PA and PB are tangents from an external point P to a circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN. [CBSE 2010]
Solution:
Given : In the figure, PA and PB are the tangents to the circle with centre O from a point P outside it LN touches it at M
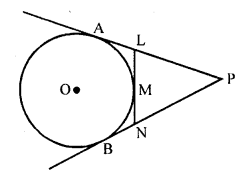
To prove : PL + LM = PN + MN
Prove : PA and PB are tangents to the circle from P
PA = PB
Similarly from L, LA and LM are tangents
LA = LM
Similarly NB = NM
Now PA = PB => PL + LA = PN + NB
PL + LM = PN + NM
Hence proved.
Question 29.
In the figure, BDC is a tangent to the given circle at point D such that BD = 30 to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF (ii) radius of the circle.
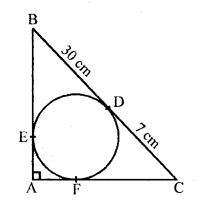
Solution:
In the figure, BDC is a tangent to the given circle with centre O and D is a point such that
BD = 30 cm and CD = 7 cm
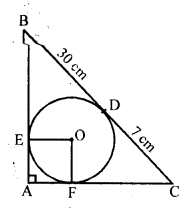
BE and CF are other two tangents drawn from B and C respectively which meet at A on producing this and ∆BAC is a right angle so formed
To find : (i) AF and (ii) radius of the circle
Join OE and OF
OE = OF radii of the circle
OE ⊥ AB and OF ⊥ AC
OEAF is a square
BD and BE are the tangents from B
BE = BD = 30 cm and similarly
CF = CD = 7 cm
Let r be the radius of the circle
OF = AF = AE = r
AB = 30 + r and AC = 7 + r and BC = 30 + 7 = 37 cm
Now in right ∆ABC

Question 30.
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, prove that \({ d }_{ 2 }^{ 2 }={ c }^{ 2 }+{ d }_{ 1 }^{ 2 }\). [NCERT Exemplar]
Solution:
Let AB be a chord of a circle which touches the other circle at C. Then ∆OCB is right triangle.
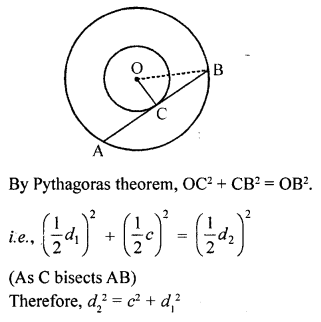
Question 31.
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS. [CBSE 2015, NCERT Exemplar]
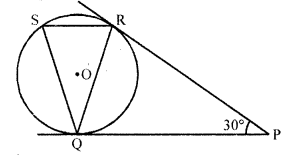
Solution:
In the given figure,
PQ and PR are tangents to the circle with centre O drawn from P
∠RPQ = 30°
Chord RS || PQ is drawn
To find ∠RQS
PQ = PR (tangents to the circle)
∠PRQ = ∠PQR But ∠RPQ = 30°
Question 32.
From an external point P, tangents PA = PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB. [CBSE 2016]
Solution:
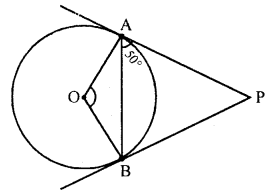
PA = PB [tangents drawn from external point are equal]
∠PBA = ∠PAB = 50° [angles equal to opposite sides]
∠APB = 180° – 50° – 50° = 80° [angle-sum property of a A]
In cyclic quad. OAPB
∠AOB + ∠APB = 180° [sum of opposite angles of a cyclic quadrilateral is 180°]
∠AOB + 80° = 180°
∠AOB = 180°- 80° = 100°
Question 33.
In the figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
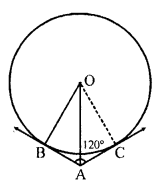
Solution:
Given : In the figure, O is the centre of the circle.
AB and AC are the tangents to the circle from A such that
∠BAC = 120° .
To prove : OA = 2AB
Proof : In ∆OAB and ∆OAC
∠OBA = ∠OCA – 90° (OB and OC are radii)
OA = OA (common)
OB = OC (radii of the circle)
∆OAB ~ ∆OAC
∠OAB = ∠OAC = 60°
Now in right ∆OAB,
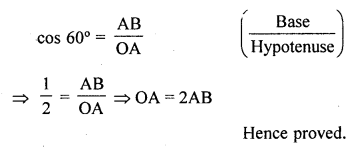
Question 34.
The lengths of three concecutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
Solution:
In quadrilateral ABCD which is circumerscribing it
BC = 4 cm, CD = 5 cm and DA = 7 cm
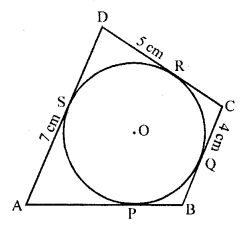
We know that if a quad, is circumscribed in a circle, then
AB + CD = AD + BC
=> AB + 5 = 4 + 7
=> AB + 5 = 11
AB = 11 – 5 = 6
AB = 6 cm
Question 35.
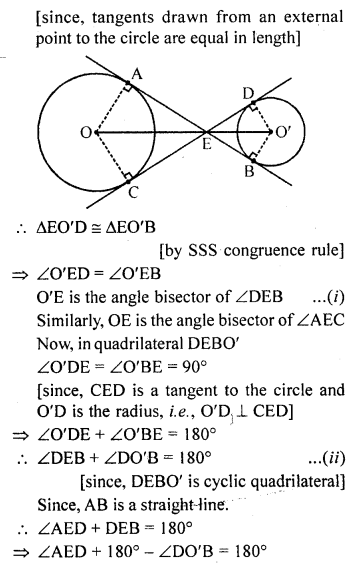
The common tangents AB and CD to two circles with centres O and O’ intersect at E between their centres. Prove that the points O, E and O’ are collinear. [NCERT Exemplar]
Solution:
Joint AO, OC and O’D, O’B
Now, in ∆EO’D and ∆EO’B
O’D = O’B [radius]
O’E = O’E [common side]
ED = EB

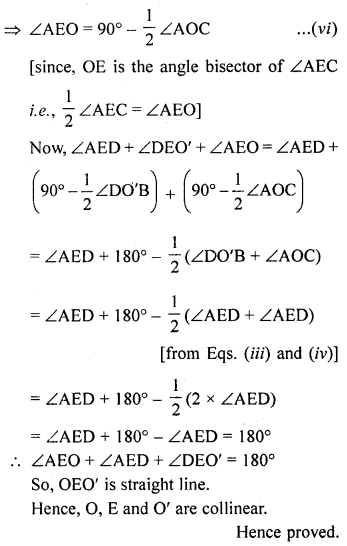
Question 36.
In the figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
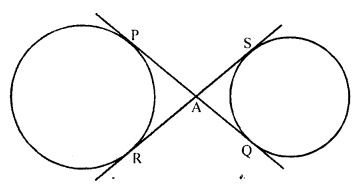
Solution:
Given : Two common tangents PQ and RS intersect each other at A.
To prove : PQ = RS
Proof: From A, AQ and AR are two tangents are drawn to the circle with centre O.
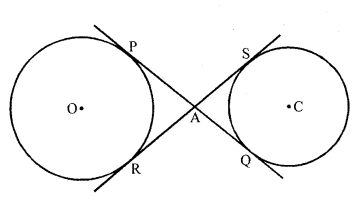
AP = AR ….(i)
Similarly AQ and AS are the tangents to the circle with centre C
AQ = AS ….(ii)
Adding (i) and (ii)
AP + AQ = AR + AS
=> PQ = RS
Hence proved.
Question 37.
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle. [CBSE 2014]
Solution:
Let R be the radius of outer circle and r be the radius if small circle of two concentric circle
AB is the chord of the outer circle and touches the smaller circle at P
Join OP, OA
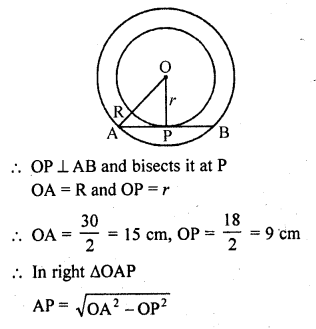

Question 38.
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD. [NCERT Exemplar]
Solution:
Given : AB and CD are tangents to two circles of equal radii.
To prove :
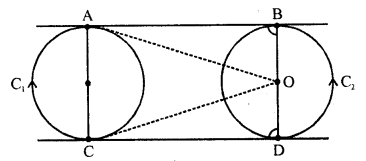
Construction : Join OA, OC, O’B and O’D
Proof: Now, ∠OAB = 90°
[tangent at any point of a circle is perpendicular to radius through the point of contact]
Thus, AC is a straight line.
Also, ∠OAB + ∠OCD = 180°
AB || CD
Similarly, BD is a straight line and ∠O’BA = ∠O’DC = 90°
Also, AC = BD
[radii of two circles are equal] In quadrilateral ABCD,
∠A = ∠B = ∠C = ∠D = 90°
andAC = BD
ABCD is a rectangle
Hence, AB = CD
[opposite sides of rectangle are equal]
Question 39.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm², find the sides PQ and PR. [CBSE 2014]
Solution:
∆PQR is circumscribed by a circle with centre O and radius 8 cm
T is point of contact which divides the line segment OT into two parts such that
QT = 14 cm and TR = 16 cm
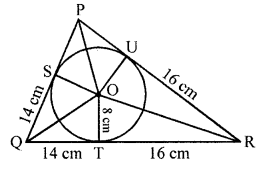
Area of ∆PQR = 336 cm²
Let PS = x cm
QT and QS are tangents to the circle from Q
QS = QT = 14 cm
Similarly RU and RT are tangents to the circle
RT = RU = 16 cm
Similarly PS and PU are tangents from P
PS = PU = x
Now PQ = x + 14 and PR = x + 16 and QR = 14 + 16 = 30 cm
Now area of ∆PQR = Area of ∆POQ + area of ∆QOR + area of ∆POR
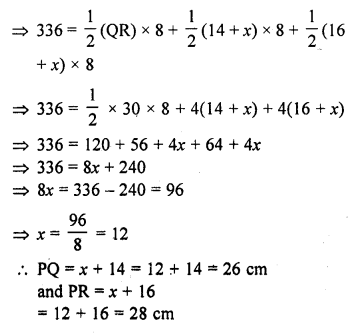
Question 40.
In the figure, the tangent at a point C of a circle and a diameter AB when extended itersect at P. If ∠PCA = 110°, find ∠CBA. [NCERT Exemplar]
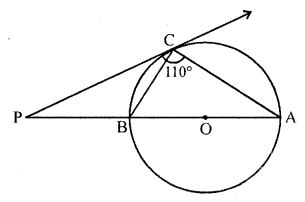
Solution:
Here, AB is a diameter of the circle from point C and a tangent is drawn which meets at a point P.
Join OC. Here, OC is radius.
Since, tangent at any point of a circle is perpendicular to the radius through point of contact circle.
OC ⊥ PC
Now, ∠PCA = 110° [given]
=> ∠PCO + ∠OCA = 110°
=> 90° + ∠OCA = 110°
=> ∠OCA = 20°
OC = OA = Radius of circle
∠OCA = ∠OAC = 20°
[since, two sides are equal, then their opposite angles are equal]
Since, PC is a tangent, so
∠BCP = ∠CAB = 20°
[angles in a alternate segment are equal]
In ∆PBC, ∠P + ∠C + ∠A= 180°
∠P = 180° – (∠C + ∠A)
∠P = 180° – (110° + 20°)
∠P = 180° – 130° = 50°
In ∆PBC,
∠BPC + ∠PCB + ∠PBC = 180°
[sum of all interior angles of any triangle is 180°]
=> 50° + 20° + ∠PBC = 180°
=> ∠PBC = 180° – 70°
∠PBC = 110°
Since, ∆PB is a straight line.
∠PBC + ∠CBA = 180°
∠CBA = 180° – 110° = 70°
Question 41.
AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in the figure. Prove that ∠BAT = ∠ACB. [NCERT Exemplar]
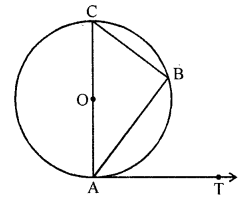
Solution:
Since, AC is a diameter line, so angle in semicircle makes an angle 90°.
∠ABC = 90° [by property]
In ∆ABC,
∠CAB + ∠ABC + ∠ACB = 180°
[ sum of all interior angles of any triangle is 180°]
=> ∠CAB + ∠ACB = 180° – 90° = 90° ……….(i)
Since, diameter of a circle is perpendicular to the tangent.
i.e. CA ⊥ AT
∠CAT = 90°
=> ∠CAB + ∠BAT = 90° …….(ii)
From Eqs. (i) and (ii),
∠CAB + ∠ACB = ∠CAB + ∠BAT
=> ∠ACB = ∠BAT
Hence proved.
Question 42.
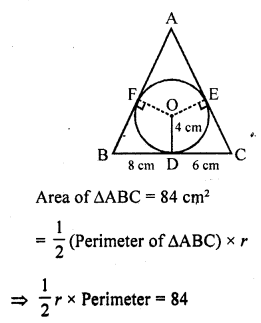
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm². [CBSE 2015]
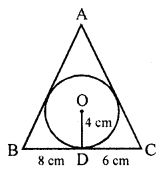
Solution:
In the given figure,
In ∆ABC is circle is inscribed touching it at D, E and F respectively.
Radius of the circle (r) = 4cm
OD ⊥ BC, then
OD = 4 cm, BD = 8 cm, DC = 6 cm
Join OE and OF

Question 43.
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ. [CBSE 2015]
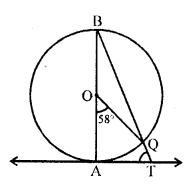
Solution:
In the given figure,
AB is the diameter, AT is the tangent
and ∠AOQ = 58°
To find ∠ATQ
Arc AQ subtends ∠AOQ at the centre and ∠ABQ at the remaining part of the circle
∠ABQ = \(\frac { 1 }{ 2 }\) ∠AOQ = \(\frac { 1 }{ 2 }\) x 58° = 29°
Now in ∆ABT,
∠BAT = 90° ( OA ⊥ AT)
∠ABT + ∠ATB = 90°
=> ∠ABT + ∠ATQ = 90°
=> 29° + ∠ATQ = 90°
=> ∠ATQ = 90°- 29° = 61°
Question 44.
In the figure, OQ : PQ = 3:4 and perimeter of ∆POQ = 60 cm. Determine PQ, QR and OP.
Solution:
In the figure, OQ : PQ = 3:4
Perimeter of ∆POQ = 60 cm
To find PQ, QR and OP
OQ : PQ = 3 : 4
Let OQ = 3x and PQ = 4x
Now in right ∆OPQ,
OP² = OQ² + PQ² = (3x)² + (4x)² = 9x² + 16x² = 25x² = (5x)²
OP = 5x
But OQ + QP + OP = 60 cm
3x + 4x + 5x = 60
=> 12x = 60
x = 5
PQ = 4x = 4 x 5 = 20 cm
QR = 2 OQ = 2 x 3x = 6 x 5 = 30 cm
OP = 5x = 5 x 5 = 25 cm
Question 45.
Equal circles with centre O and O’ touch each other at X. OO’ produced to meet a circle with centre O’, at A. AC is a tangent to the circle whose centre is O. O’ D is perpendicular to AC. Find the value of \(\frac { DO’ }{ CO }\)
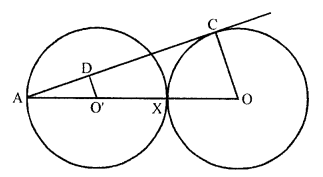
Solution:
Two equal circles with centre O and O’ touch each other externally at X
OO’ produced to meet at A
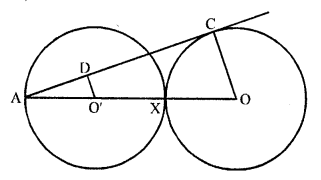
AC is the tangent of circle with centre O,
O’D ⊥ AC is drawn OC is joined
AC is tangent and OC is the radius
OC ⊥ AC
O’D ⊥ AC
OC || O’D
Now O’A = \(\frac { 1 }{ 2 }\) A x or \(\frac { 1 }{ 2 }\) AO
Now in O’AD and AOAC
∠A = ∠A (common)
∠AO’D = ∠AOC (corresponding angles)
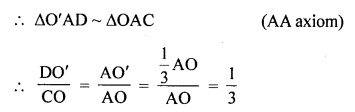
Question 46.
In the figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ∆AEO ~ ∆ABC.
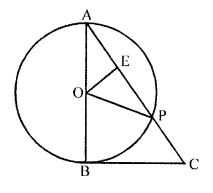
Solution:
Given : In the figure, BC is a tangent to the circle with centre O at B.
AB is diameter AC is joined which intersects the circle at P
OE bisects AP
To prove : ∆AEO ~ ∆ABC
Proof: In ∆OAE and ∆OPE
OE = OE (common)
OA = OP ‘ (radii of the same circle)
EA = EP (given)
∆OAE = ∆OPE (SSS axiom)
∠OEA = ∠OEP
But ∠OEA + ∠OEP = 180°
∠OEA = 90°
Now in ∆AEO and ∆ABC
∠OEA = ∠ABC (each 90°)
∠A = ∠A (common)
∆AEO ~ ∆ABC (AA axiom)
Hence proved.
Question 47.
In the figure, PO ⊥ QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisectors of each other.
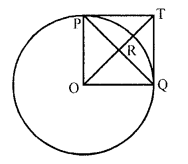
Solution:
Given : In the figure, O is the centre of the circle
PO ⊥ QO
They tangents at P and Q intersect each other at T
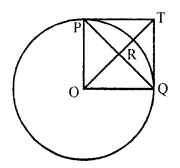
To prove : PQ and OT are right bisector of each other
Proof : PT and QT are tangents to the circle
PT = QT
OP and OQ are radii of the circle and ∠POQ = 90° ( PO ⊥ QO)
OQTP is a square Where PQ and OT are diagonals
Diagonals of a square bisect each other at right angles
PQ and OT bisect each other at right angles
Hence PQ and QT are right bisectors of each other.
Question 48.
In the figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.
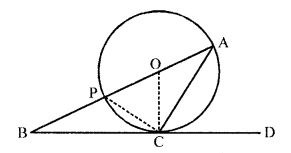
Solution:
Given : In the figure, O is the centre of the circle BCD is a tangent, CP is a chord
prove : ∠BAC + ∠ACD = 90°
Proof: ∠ACD = ∠CPA (Angles in the alternate segment)
But in ∆ACP,
∠ACP = 90° (Angle in a semicircle)
∠PAC + ∠CPA = 90°
=> ∠BAC + ∠ACD = 90°
(∠ACD = ∠CPA proved)
Hence proved.
Question 49.
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines. [NCERT Exemplar]
Solution:
Given : Two tangents PQ and PR are drawn from an external point P to a circle with centre O.
To prove : Centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
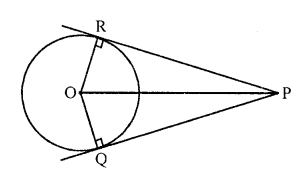
Construction : Join OR, and OQ.
In ∆POR and ∆POQ
∠PRO = ∠PQO = 90°
[tangent at any point of a circle is perpendicular to the radius through the point of contact]
OR = OQ [radii of same circle]
Since, OP is common.
∆PRO = ∆PQO [RHS]
Hence, ∠RPO = ∠QPO [by CPCT]
Thus, O lies on angle bisector of PR and PQ.
Hence proved.
Question 50.
In the figure, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the lengths of PS. [CBSE 2017]
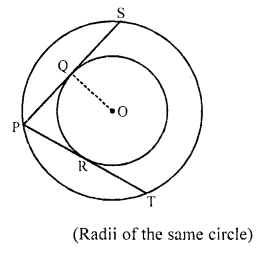
Solution:
Construction : Join OS and OP.
Consider ∆POS
We have,
PO = OS
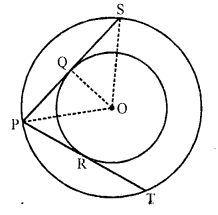
∆POS is an isosceles triangle.
We know that in an isosceles triangle, if a line drawn perpendicular to the base of the triangle from the common vertex of the equal sides, then that line will bisect the base (unequal side).
And PQ = PR = 5 cm
[PRT and PQS are tangents to the inner circle to the inner circle from a point P lying on the outer circle]
We have, PQ = QS
It is given that, PQ = 5 cm
QS = 5 cm
From the figure, we have
PS = PQ + QS
=> PS = 5 + 5
=> PS = 10 cm
Question 51.
In the figure, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOP is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2. [CBSE 2017]
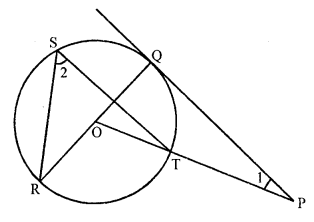
Solution:
Construction : Join RT.
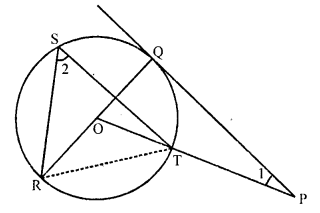
Given, ∠POR = 130°
∠POQ = 180°- (∠POR) = 180° – 130° = 50°
Since, PQ is a tangent
∠PQO = 90°
Now, In ∆POQ,
∠POQ + ∠PQO + ∠QPO = 180°
=> 50° + 90° + ∠1 = 180°
=> ∠1 = 180° – 140°
=> ∠1 = 40°
Now, In ∆RST
∠RST = \(\frac { 1 }{ 2 }\) ∠ROT
[Angle which is subtended by on arc at the centre of a circle is double the size of the angle subtended at any point on the circumference]
=> ∠2 = \(\frac { 1 }{ 2 }\) x 130° = 65°
Now ∠1 + ∠2 = 40° + 65° = 105°
Question 52.
In the figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC = PD. [CBSE 2017]
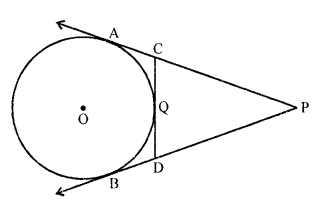
Solution:
PA = PB = 12 cm …(i)
QC = AC = 3cm …(ii)
QD = BD = 3 cm …(iii)
[Tangents drawn from an external point are equal]
To find : PC + PD
= (PA – AC) + (PB – BD)
= (12 – 3) + (12 – 3) [From (i), (ii), and (iii)]
= 9 + 9 = 18 cm
Hope given RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.