Class 6 Maths Chapter 5 Prime Time Notes
Class 6 Maths Chapter 5 Notes – Class 6 Prime Time Notes
Factors and Multiples
A factor of a number is an exact divisor of that number i.e. the factor divides the number completely without leaving any remainder.
For example, 1, 2, 3, and 6 are exact divisors of 6. So, 1, 2, 3, and 6 are factors of 6.
A number is a multiple of each of its factors.
For example, when 12 = 3 × 4, we can say that 12 is a multiple of 3 and 4.

Let us discuss some points about factors and multiples.
(i) 1 is a factor of every number.
(ii) Every number is a factor of itself.
(iii) Every factor is less than or equal to the given number.
(iv) The number of factors of a given number is finite.
e.g. The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 and 96 which are finite.
(v) Every multiple of a number is greater than or equal to that number.
e.g. Multiples of 3 are 3, 6, 9, 12, 15,…
(vi) The number of multiples of a given number is infinite.
e.g. Multiples of 4 are 4, 8, 12, 16, 20, …
(vii) Every number is a multiple of itself.
e.g. 7 = 7 × 1 and 11 = 11 × 1.
![]()
Example 1.
Write all the possible factors of the following numbers.
(i) 16
(ii) 30
(iii) 27
(iv) 19
Solution:
(i) Here, 16 = 1 × 16, 16 = 2 × 8, 16 = 4 × 4
∴ Factors of 16 are 1, 2, 4, 8 and 16.
(ii) Here, 30 = 1 × 30, 30 = 2 × 15, 30 = 3 × 10, 30 = 5 × 6
∴ Factors of 30 are 1, 2, 3, 5,6, 10,15 and 30.
(iii) Here, 27 = 1 × 27, 27 = 3 × 9
∴ Factors of 27 are 1, 3, 9 and 27.
(iv) Here, 19 = 1 × 19
∴ Factors of 19 are 1 and 19.
Note it 0 is not the factor of any number.
Example 2.
Write the first four multiples of the following numbers.
(i) 5
(ii) 12
(iii) 13
Solution:
(i) Multiples of 5 are 5 × 1 = 5, 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20
Hence, the first four multiples of 5 are 5, 10, 15 and 20.
(ii) Multiples of 12 are 12 × 1 = 12, 12 × 2 = 24, 12 × 3 = 36, 12 × 4 = 48
Hence, the first four multiples of 12 are 12, 24, 36 and 48.
(iii) Multiples of 13 are 13 × 1 = 13, 13 × 2 = 26, 13 × 3 = 39, 13 × 4 = 52
Hence, the first four multiples of 13 are 13, 26, 39 and 52.
Common Multiples and Common Factors
Common Multiples
The multiples which are common to each of the given numbers are called their common multiples.
e.g. 15 is a common multiple of 3 and 5.
Example 3.
Find all the multiples of 50 that lie between 340 and 460.
Solution:
The multiples of 50 that lie between 340 and 460 are 350, 400 and 450.
Example 4.
Find the first three common multiples of
(i) 2 and 3
(ii) 12 and 18
Solution:
(i) Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18,…..
Multiple of 3 are 3, 6, 9, 12, 15, 18,…..
Hence, the first three common multiples of 2 and 3 are 6, 12, and 18.
(ii) Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108,…..
Multiples of 18 are 18, 36, 54, 72, 90, 108,……
Hence, the first three common multiples of 12 and 18 are 36, 72, and 108.
Example 5.
Write all the numbers less than 100 which are common multiples of 4 and 5.
Solution:
Multiples of 4 less than 100 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96.
Multiples of 5 less than 100 are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95.
Hence, the common multiples of 4 and 5 less than 100 are 20, 40, 60 and 80.
Common Factors
The factors which are common in each of the given numbers are called their common factors.
e.g. 3 is a common factor of 9 and 15 as 3 each divides both 9 and 15.
Example 6.
Find the common factors of
(i) 8 and 20
(ii) 35 and 50
(iii) 6, 12 and 18
(iv) 8, 16 and 24
Solution:
(i) Factors of 8 = 1, 2, 4, 8
Factors of 20 = 1, 2, 4, 5, 10, 20
Hence, the common factors of 8 and 20 are 1, 2, and 4.
(ii) Factors of 35 = 1, 5, 7, 35
Factors of 50 = 1, 2, 5, 10, 25, 50
Hence, the common factors of 35 and 50 are 1 and 5.
(iii) Factors of 6 = 1, 2, 3, 6
Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 18 = 1, 2, 3, 6, 9, 18
Hence, the common factors of 6, 12, and 18 are 1, 2, 3 and 6.
(iv) Factors of 8 = 1, 2, 4, 8
Factors of 16 = 1, 2, 4, 8, 16
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Hence, the common factors of 8, 16, and 24 are 1, 2, 4, and 8.
Example 7.
Find the common factors of
(i) 15 and 25
(ii) 12, 18 and 36
Solution:
(i) Factors of 15 = 1, 3, 5, 15
Factors of 25 = 1, 5, 25
Hence, the common factors of 15 and 25 are 1 and 5.
(ii) Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Hence, the common factors of 12, 18, and 36 are 1, 2, 3, and 6.
Example 8.
A number is divisible by 14. By what other numbers will that number be divisible?
Solution:
If any number is divisible by 14, then this number will also be divisible by the factors of 14 i.e. by 1, 2, and 7.
Example 9.
A number is divisible by 2, 3, and 5. By which other numbers will that number be always divisible?
Solution:
If a number is divisible by 2, 3, and 5, then it is always divisible by its products i.e. 2 × 3 × 5 = 30
If a number is divisible by any two or more numbers, then it is always divisible by their products.
![]()
Perfect Number
A number for which the sum of all its factors is equal to twice the number is called a perfect number.
e.g. 6, 28, 496,…..
Example 10.
Find all the perfect numbers between 1 and 50.
Solution:
The perfect numbers between 1 and 50 are 6 and 28.
The factor of 6 is 1, 2, 3 and 6.
Sum of factors = 1 + 2 + 3 + 6 = 12
Since, 12 = 2 × 6
∴ The sum of factors is equal to twice the number.
So, 6 is a perfect number.
Factors of 28 are 1, 2, 4, 7, 14 and 28.
Sum of factors = 1 + 2 + 4 + 7 + 14 + 28 = 56
Since, 56 = 2 × 28
∴ The sum of factors is equal to twice the number.
So, 28 is a perfect number.
Example 11.
Find the common factors of
(i) 25 and 80
(ii) 42 and 70
(iii) 56, 120
(iv) 9 and 12
(v) 7, 14 and 28
(vi) 12, 18 and 15
(vii) 6, 9, 16 and 27
(viii) 4, 12 and 16
Solution:
(i) 1, 5
(ii) 1, 2, 7, 14
(iii) 1, 2, 4 and 8
(iv) 1 and 3
(v) 1, 7
(vi) 1 and 3
(vii) 1
(viii) 1, 2 and 4
Example 12.
A number is divisible by 8. By what other numbers will that number be divisible?
Solution:
1, 2, 4
Example 13.
4096 is divisible by 64. Can we say it is divisible by 8 also?
Solution:
Yes, it is divisible by 8 also.
Example 14.
A number is divisible by 6, 5, and 7. By which other numbers will that number be always divisible?
Solution:
210
Example 15.
A number is divisible by 3, 4, 5, and 13. Is that number also divisible by 780?
Solution:
Yes
Example 16.
Find the first three common multiples of
(i) 5 and 15
(ii) 8 and 12
(iii) 6 and 8
(iv) 7 and 14
Solution:
(i) 15, 30, 45
(ii) 24, 48, 72
(iii) 24, 48, 72
(iv) 14, 28 and 42
Example 17.
Write all the numbers less than 100 which are common multiples of 7 and 8.
Solution:
56
Example 18.
Write all the perfect numbers from 1 to 20.
Solution:
6
Example 19.
Find all the multiples of 20 that lie between 250 and 350.
Solution:
260, 280, 300, 320, 340
![]()
Example 20.
Find any three numbers that are multiples of 20 but not multiples of 40.
Solution:
20, 60, 100
Prime Numbers
Prime Numbers
The numbers other than 1, whose only factors are 1 and the number itself are called prime numbers.
e.g. 2, 3, 5, 7, 11,…, etc. are prime numbers.
2 is the smallest prime number which is even and every prime number except 2 is odd.
Two prime numbers whose difference is 2 are called twin prime numbers.
Method of Finding Prime Numbers from 1 to 100
Step I: List all numbers from 1 to 100.
Step II: Cross out 1 because it is not a prime number.
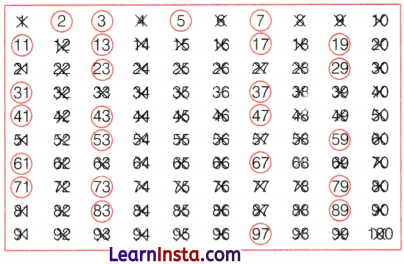
Step III: Encircle 2, cross out all the multiples of 2, other than 2 itself i.e. 4, 6, 8, and so on.
Step IV: You will find that the next uncrossed number is 3. Encircle 3 and cross out all the multiples of 3, other than 3 itself.
Step V: The next uncrossed number is 5. Encircle 5 and cross out all the multiples of 5, other than 5 itself.
Step VI: Continue this process till all the numbers in the list are either encircled or crossed out.
All the encircled numbers are prime numbers. All the crossed-out numbers, other than 1 are composite. This method is called the Sieve of Eratosthenes which was invented by Greek mathematician Eratosthenes.
Example 1.
Check whether the following numbers are prime or not.
(i) 17
(ii) 39
(iii) 41
(iv) 56
Solution:
(i) 17 = 1 × 17, 17 = 17 × 1
Since 17 has only two factors i.e. 1 and 17.
Therefore, 17 is a prime number.
(ii) 39 = 1 × 39, 39 = 3 × 13
Since, 39 has four factors i.e. 1, 3, 13, and 39.
Therefore, 39 is not a prime number.
(iii) 41 = 1 × 41, 41 = 41 × 1
Since 41 has only two factors i.e. 1 and 41.
Therefore, 41 is a prime number.
(iv) 56 = 1 × 56, 56 = 2 × 28, 56 = 4 × 14, 56 = 7 × 8
Since, 56 has eight factors i.e. 1, 2, 4, 7, 8, 14, 28, and 56.
Therefore, 56 is not a prime number.
Example 2.
Give two pairs of prime numbers whose difference is 2.
Solution:
Two pairs of prime numbers whose difference is 2 are
(i) 3 and 5 (i.e. 5 – 3 = 2)
(ii) 29 and 31 (i.e. 31 – 29 = 2)
Example 3.
Observe that 3 × 4 + 1 = 13 is a prime number. Here, 1 has been added to a multiple of 3 to get a prime number. Give some more examples of this type.
Solution:
Some more examples of this type are 3 × 2 + 1 = 7, 3 × 6 + 1 = 19, 3 × 10 + 1 = 31, 3 × 12 + 1 = 37, 3 × 14 + 1 = 43, 3 × 20 + 1 = 61
Here, all numbers 7, 19, 31, 37, 43, and 61 are prime numbers as 1 has been added to the multiples of 3 to get these prime numbers.
Example 4.
Find the greatest prime number between 10 and 20.
Solution:
Prime numbers between 10 and 20 are 11, 13, 17 and 19.
Therefore, the greatest prime number between 10 and 20 is 19.
Example 5.
Write four pairs of prime numbers less than 20, whose sum is divisible by 8.
Solution:
Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17 and 19.
Here, 3 + 5 = 8 (divisible by 8)
5 + 11 = 16 (divisible by 8)
11 + 13 = 24 (divisible by 8)
13 + 19 = 32 (divisible by 8)
Hence, four pairs of prime numbers whose sum is divisible by 8 are (3, 5), (5, 11), (11, 13) and (13, 19).
Example 6.
The numbers 17 and 71 are prime numbers. Both these numbers have the same digits 1 and 7. Find the such pairs of prime numbers upto 100.
Solution:
All prime numbers upto 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
Out of these, pairs of prime numbers having the same digits are (13, 31), (17, 71), (37, 73) and (79, 97).
Hence, there are 4 pairs of such types.
Example 7.
Express the following as the sum of two odd prime numbers.
(i) 32
(ii) 40
(iii) 34
Solution:
(i) We have, 32 = 29 + 3
(ii) We have, 40 = 37 + 3
(iii) We have, 34 = 31 + 3 or 29 + 5
![]()
Example 8.
Express each of the following numbers as the sum of three odd primes.
(i) 41
(ii) 25
(iii) 27
(iv) 71
Solution:
(i) We have, 41 = 11 + 13 + 17, where 11, 13, and 17 are odd prime numbers.
(ii) We have, 25 = 5 + 7 + 13, where 5, 7, and 13 are odd prime numbers.
(iii) We have, 27 = 3 + 5 + 19, where 3, 5, and 19 are odd prime numbers.
(iv) We have, 71 = 13 + 17 + 41, where 13, 17, and 41 are odd prime numbers.
Composite Numbers
The numbers having more than two factors are called composite numbers.
e.g. 4, 6, 8, 9, 10,…, etc. are composite numbers.
1 is neither a prime number nor a composite number because it has only one factor.
Example 9.
Write all the prime and composite numbers less than 15.
Solution:
Prime numbers less than 15 are 2, 3, 5, 7, 11 and 13.
Composite numbers less than 15 are 4, 6, 8, 9, 10, 12 and 14.
Example 10.
Write five consecutive composite numbers less than 100, so that there is no prime number between them.
Solution:
Five consecutive composite numbers of such type are 54, 55, 56, 57, and 58.
Example 11.
State whether the following statements are true or false.
(i) The sum of three even numbers is even.
(ii) The sum of two odd numbers and one even number is odd.
(iii) All prime numbers are even.
(iv) The sum of two prime numbers is always odd.
(v) The product of two even numbers is always odd.
Solution:
(i) True, because the sum of three even numbers is always even.
e.g. 2 + 4 + 6 = 12 (even)
(ii) False, because the sum of two odd numbers and one even number is always an even number.
e.g. 1 + 5 + 4 = 10 (even)
(iii) False, because 2 is only an even prime number. So, all prime numbers are not even.
(iv) False, because the sum of two prime numbers is either odd or even.
e.g. 3 + 5 = 8 (even) and 2 + 3 = 5 (odd)
(v) False, because the product of two even numbers is always even.
e.g. 4 × 6 = 24
Example 12.
Fill in the blanks.
(i) The numbers other than 1 whose only factors are 1 and the number itself are called ___________
(ii) The smallest odd prime number is ___________
(iii) Two prime numbers whose difference is 2 are called ___________
(iv) ___________ is the smallest prime number which is even.
Solution:
(i) The numbers other than 1 whose only factors are 1 and the number itself are called prime numbers.
(ii) The smallest odd prime number is 3.
(iii) Two prime numbers whose difference is 2 are called twin primes.
(iv) 2 is the smallest prime number which is even.
Example 13.
Check whether the following numbers are prime or not.
(i) 11
(ii) 16
(iii) 19
(iv) 43
Solution:
(i) Yes
(ii) No
(iii) No
(iv) Yes
Example 14.
What is the difference between the highest prime number and the least prime number between 1 to 50?
Solution:
45
Example 15.
Give four pairs of prime numbers whose difference is 2.
Solution:
(5, 7), (11, 13), (17, 19), (41, 43)
Example 16.
Observe that 5 × 3 + 2 = 17 is a prime number. Here, 2 has been added to a multiple of 5 to get a prime number. Give some more examples of this type.
Solution:
5 × 1 + 2 = 7
5 × 7 + 2 = 37
5 × 9 + 2 = 47
5 × 13 + 2 = 67
5 × 19 + 2 = 97
Example 17.
Find the greatest prime number between 20 and 50.
Solution:
47
![]()
Example 18.
Write four pairs of prime numbers less than 40 whose sum is divisible by 7.
Solution:
(2, 5), (3, 11), (11, 17), (5, 37)
Example 19.
Express the following as the sum of two odd prime numbers.
(i) 26
(ii) 38
(iii) 48
(iv) 60
Solution:
(i) 7 + 19
(ii) 7 + 31
(iii) 7 + 41
(iv) 7 + 53
Example 20.
Express each of the following numbers as the sum of three odd primes.
(i) 21
(ii) 31
(iii) 23
(iv) 49
Solution:
(i) 3 + 5 + 13
(ii) 5 + 7 + 19
(iii) 5 + 7 + 11
(iv) 13 + 17 + 19
Example 21.
Write all the prime and composite numbers between 10 to 25.
Solution:
Prime numbers = 11, 13, 17, 19, 23
Composite numbers = 12, 14, 15, 16, 18, 20, 21, 22, 24
Example 22.
Write five consecutive composite numbers less than 50, so that there is no prime number between them.
Solution:
24, 25, 26, 27 and 28.
Example 23.
State whether the following statements are true or false.
(i) All prime numbers are odd.
(ii) The sum of three odd numbers is an even number.
(iii) Prime numbers do not have any factor.
(iv) The product of three odd numbers is odd.
(v) All odd numbers are composite numbers.
(vi) Two consecutive numbers cannot be both even.
Solution:
(i) False
(ii) False
(iii) False
(iv) True
(v) False
(vi) True
Example 24.
Fill in the blanks.
(i) The smallest even composite number is ___________
(ii) 1 is neither ___________ nor ___________ number.
(iii) Except ___________, all the prime numbers are odd.
(iv) The smallest odd composite number is ___________
Answer:
(i) 4
(ii) Prime, Composite
(iii) 2
(iv) 9
Prime Factorisation
If a natural number is expressed as the product of prime numbers, then the factorization of the number is called its prime factorization.
Example 1.
Find the prime factorization of 630.
Solution:
By division method,

∴ 630 = 2 × 3 × 3 × 5 × 7 which is the required prime factorisation.
Example 2.
Write the smallest 4-digit number and all its prime factors.
Solution:
Smallest 4-digit number = 1000

∴ Prime factors of 1000 = 2 × 2 × 2 × 5 × 5 × 5
Example 3.
Write the greatest 5-digit number and all its prime factors.
Solution:
Greatest 5-digit number = 99999

∴ Prime factors of 99999 = 3 × 3 × 41 × 271
Example 4.
In which of the following expression, prime factorization has been done?
(i) 36 = 2 × 3 × 6
(ii) 54 = 2 × 3 × 3 × 3
(iii) 56 = 2 × 4 × 7
(iv) 76 = 2 × 2 × 19
Solution:
(i) We have, 36 = 2 × 3 × 6
Here, 6 is not a prime number.
So, it is not the prime factorization of 36.
(ii) We have, 54 = 2 × 3 × 3 × 3
Here, 2 and 3 are prime numbers.
So, it is the prime factorization of 54.
(iii) We have, 56 = 2 × 4 × 7
Here, 4 is not a prime number.
So, it is not the prime factorization of 56.
(iv) We have, 76 = 2 × 2 × 19
Here, 2 and 19 are prime numbers.
So, it is a prime factorization of 76.
Example 5.
I am the smallest number, having four different odd prime factors. Can you find me?
Solution:
Since the number is the smallest, so four different smallest odd prime factors are 3, 5, 7, and 11.
∴ The smallest number having four different odd prime factors = 3 × 5 × 7 × 11 = 1155.
![]()
Example 6.
Write all the prime factors of 105 and arrange them in ascending order. Is there is any relation between the two consecutive prime factors?
Solution:
Prime factorisation of 105
∴ 105 = 3 × 5 × 7

The ascending order of prime factors of 105 is 3, 5, 7.
Here, 5 – 3 = 2 and 7 – 5 = 2
So, the relation between two consecutive prime factors of 105 is that the difference of two consecutive prime factors is 2.
Coprime Numbers
Two numbers that have only 1 as their common factor are called coprime numbers.
Any two prime numbers are always coprimes but two co-prime numbers need not be prime numbers.
Example 7.
Which of the following pairs are coprimes?
(i) 8, 25
(ii) 4, 10
Solution:
(i) Factors of 8 = 1, 2, 4, 8
Factors of 25 = 1, 5, 25
∴ 8 and 25 have only 1 as a common factor.
∴ 8 and 25 are co-prime numbers.
(ii) Factors of 4 = 1, 2, 4
Factors of 10 = 1, 2, 5, 10
∴ 4 and 10 have 1, and 2 as common factors.
∴ 4 and 10 are not co-prime numbers.
Example 8.
Use prime factorization to check whether 27 and 51 are coprime.
Solution:
Prime factorization of 27 and 51.
27 = 3 × 3 × 3 and 51 = 3 × 17
They have common factors 3.
Thus, 27 and 51 are not coprime.
Using prime factorization to check if one number is divisible by another
If one number is divisible by another number, the prime factorization of the second number is entirely contained within the prime factorization of the first number.
Example 9.
Use prime factorization to check if 144 is divisible by 16.
Solution:
Prime factorization of 16 and 144
16 = 2 × 2 × 2 × 2
144 = 2 × 2 × 2 × 2 × 3 × 3
Since we can multiply in any order,
144 = 16 × 3 × 3
Therefore, 144 is divisible by 16.
Example 10.
Is 42 divisible by 12?
Solution:
The prime factorisation of 42 and 12 are 42 = 2 × 3 × 7 and 12 = 2 × 2 × 3
All prime factors of 12 are also prime factors of 42. But the prime factorization of 12 is not included in the prime factorization of 42 because 2 occurs twice in the prime factorization 712 but only once in the prime factorization 42. Therefore, 42 is not divisible by 12.
Example 11.
Which of the following are coprime?
(i) 15 and 37
(ii) 40 and 46
(iii) 23 and 17
(iv) 22 and 33
Solution:
(i) Coprime numbers
(ii) Not coprime numbers
(iii) Coprime numbers
(iv) Not coprime numbers
Example 12.
Find the prime factorization of the following.
(i) 20570
(ii) 60775
Solution:
(i) 2 × 5 × 11 × 11 × 17
(ii) 5 × 5 × 11 × 13 × 17
Example 13.
Fill in the given space.
Prime factorisation of 47957 = 7 × 13 × _____ × 17.
Solution:
31
Example 14.
Write the smallest 8-digit number and all its prime factors.
Solution:
10000000 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5 × 5 × 5 × 5
Example 15.
Write the greatest 3-digit number and all its prime factors.
Solution:
999 = 3 × 3 × 3 × 37
Example 16.
In which of the following expressions, prime factorization has been done?
(i) 2 × 3 × 3 × 3 × 4 = 216
(ii) 2 × 3 × 7 × 7 × 7 × 11 = 22638
(iii) 3 × 3 × 7 × 7 × 6 = 2646
(iv) 3 × 5 × 7 × 7 = 735
Solution:
(ii) and (iv)
Example 17.
I am the smallest number, having five different prime factors. Can you find me?
Solution:
2310
![]()
Example 18.
Write all the prime factors of 231 and arrange them is ascending order. Is there is any relation between the two consecutive prime factors?
Solution:
3, 7, and 11, the Difference between two consecutive prime factors is 4.
Example 19.
Is 195 divisible by 15? Check using prime factorization.
Solution:
Yes
Example 20.
Find the prime factorization of the following numbers without multiplying first.
(i) 75 × 35
(ii) 105 × 15
(iii) 100 × 27
Solution:
(i) 75 × 35 = 3 × 5 × 5 × 5 × 7
(ii) 105 × 15 = 3 × 3 × 5 × 5 × 7
(iii) 100 × 27 = 2 × 2 × 3 × 3 × 3 × 5 × 5
Test for Divisibility
To check the divisibility of any number by other, we normally perform actual division and see whether the remainder is zero or not.
To check without actual division, some divisibility test of different numbers are given below.
Test of Divisibility by 2
A number is divisible by 2, if it has any of the digits 0, 2, 4, 6 or 8 at its ones place.
Example 1.
Check whether the number 246 is divisible by 2 or not.
Solution:
Here, in 246 the digit at the one’s place is 6.
Hence, 246 is divisible by 2.
Test of Divisibility by 4
A number with three or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4.
Example 2.
Check whether the number 9524624 is divisible by 4 or not.
Solution:
Given number is 9524624.
The number formed by the last two digits is 24, which is divisible by 4.
Hence, 9524624 is divisible by 4.
Test of Divisibility by 5
A number is divisible by 5 if it has either 0 or 5 in its place.
e.g. Each of the numbers 60, 225, 625 is divisible by 5.
Test of Divisibility by 8
A number with 4 or more digits is divisible by 8 if the number formed by the last three digits is divisibile by 8.
Example 3.
Check whether the number 79152 is divisible by 8 or not.
Solution:
The given number is 79152.
The number formed by last three digits is 152 which is divisible by 8.
Hence, 79152 is divisible by 8.
Example 4.
Which of the following numbers is divisible by both 4 and 8?
(i) 9638
(ii) 9640
Solution:
(i) We have, 9638
(a) Divisibility by 4
The number formed by the last two digits = 38
On dividing 38 by 4, we get the Remainder ≠ 0
∴ 38 is not divisible by 4, so 9638 is also not divisible by 4.
(b) Divisibility by 8
The number formed by the last three digits = 638
On dividing 638 by 8, we get Remainder ≠ 0
∴ 638 is not divisible by 8, so 9638 is also not divisible by 8.
So, 9638 is not divisible by both 4 and 8.
(ii) We have, 9640
(a) Divisibility by 4
Number formed by last two digits = 40
On dividing 40 by 4, we get Remainder = 0
∴ 40 is divisible by 4, so 9640 is also divisible by 4.
(b) Divisibility by 8
Number formed by last three digits = 640
On dividing 640 by 8, we get Remainder = 0
∴ 640 is divisible by 8, so 9640 is also divisible by 8.
Hence, 9640 is divisible by both 4 and 8.
Test of Divisibility by 10
A number is divisible by 10 if it has 0 at its ones place.
Example 5.
Check whether the number 49600 is divisible by 10 or not.
Solution:
The given number is 49600.
Here, the number 49600 has 0 in its place.
Therefore, 49600 is divisible by 10.
![]()
Example 6.
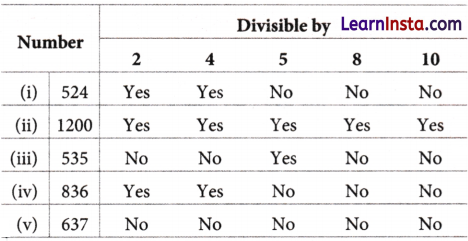
Using divisibility tests, determine which of the following numbers are divisible by 2, by 4, by 5, by 8 and by 10 (say yes or no)?
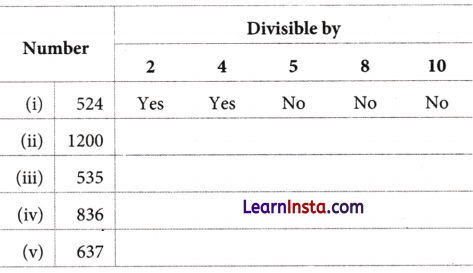
Solution:
We know that a number is divisible by
2, if it has digits 0, 2, 4, 6 or 8 at its ones place.
4, if last two digits of the number is completely divisible by 4.
5, if a number has 0 or 5 at its ones place.
8, if last three digits of the number is completely divisible by 8.
10, if a number has 0 at its ones place.
Hence, the complete table is as follows.
Example Problems
Question 1.
Using divisibility tests, determine which of the following numbers is divisible by 2.
(i) 315623
(ii) 34678
(iii) 789
(iv) 2651
Answer:
(i) Not divisible
(ii) Divisible
(iii) Not divisible
(iv) Not divisible
Question 2.
Is 494616 divisible by 4?
Answer:
Yes
Question 3.
Is the number 17152352 divisible by 4?
Answer:
Yes
Question 4.
Which of the following is divisible by 4 and 8?
(i) 1312
(ii) 1626
(iii) 1612
(iv) 2304
Answer:
(i) Not divisible
(ii) Not divisible
(iii) Not divisible
(iv) Divisible
Question 5.
Using divisibility tests, determine which of the following numbers are divisible by 2, by 4, by 5, by 8 and by 10 (say yes or no)?

Answer:
Do yourself.
→ When two numbers are multiplied then we get another number called the product.
For example,
![]()
→ This product is divisible by both of the given numbers. The given numbers are called factors of the product and the product is called the multiple of the given numbers. So, we can say, a factor of a number is an exact divisor of that number and the given number is called a multiple of each of its factors.
→ A number has finite number of factors but it has infinite number of multiples.
For example,
1, 2, 3 and 6 are four (finite) factors of 6
6, 12, 18, 24, … are (infinite) multiples of 6.
→ Numbers that have only two factors are called prime numbers or primes. Here are the first few primes — 2, 3, 5, 7, 11, 13, 17, 19,… The factors of a prime number are 1 and the number itself.
→ The rest of the numbers except 1 are composite numbers as they have more than two factors that is one more factor other than 1 and the number itself. The first few composite numbers are 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20,…
→ Every composite number can be expressed as a product of prime numbers. Such expression is called prime factorisation.
![]()
→ A number that divides a given number exactly is called a factor of the given number and the given number is called the multiple of the factor.
→ If a number is divisible by another, the second number is called a factor of the first.
→ 1 is a factor of every number and every number is a factor of itself.
→ Every factor of a number is less than or equal to the given number.
→ A number for which the sum of all its factors is equal to twice the number is called a perfect number.
→ Every multiple of a given number is greater than or equal to that number.
→ Every number is a multiple of itself.
→ A number may have an infinite number of multiples but the number of factors of a given number is finite.
→ A number greater than 1, which has only two factors namely 1 and the number itself is called a prime number.
→ Prime numbers between 1 and 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
→ ‘2’ is the smallest prime number. It is the only even prime number.
→ A number that has more than 2 factors, i.e., at least one more factor other than 1 and number itself is called composite number.
→ A natural number 1 is neither a prime nor a composite number.
→ Pairs of prime numbers which differ by 2 are called twin primes.
→ Two numbers are said to be co-prime if they do not have a common factor other than 1.
→ Every even number except 2 can be expressed as a sum of two prime numbers.
→ Every composite number has a unique prime factorisation.
![]()
→ If one number is divisible by another, the prime factorization of the second number is included in the prime factorization of the first number.
→ To check whether a pair of numbers are co-primes, we can first find their prime factorizations and look into a common prime factor. If there is no common prime factor, they are co-prime, otherwise they are not.
→ A number is divisible:
- by 2, if its unit digit is 0, 2, 4, 6, or 8.
- by 4, if the number formed by its last two digits is divisible by 4.
- by 5, if its unit digit is 0 or 5.
- by 8, if the number formed by its last three digits is divisible by 8.
- by 10, if its unit digit is 0.
→ If a number is divisible by two or more co-prime numbers, then it must be divisible by their product.