
On this page, you will find Polynomials Class 10 Notes Maths Chapter 2 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 2 Polynomials will seemingly help them to revise the important concepts in less time.
CBSE Class 10 Maths Chapter 2 Notes Polynomials
Polynomials Class 10 Notes Understanding the Lesson
1. The value of the polynomial p(x) at x = a is p(a).
2. Zeroes of the polynomial p(x) can be find by equating p(x) to zero and solving the equation for
3. If for p(x) = ax2 + bx + c = 0, a ≠ 0; α and β are the zeroes, then
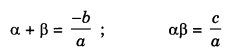
4. If for p(x) = ax3 + bx2 + cx + d = 0; a ≠ 0; α, β,γ are the zeroes, then
α + β + γ = \(\frac{-b}{a}\)
αβ+βγ + αγ = \(\frac{c}{a}\)
αβγ =\(\frac{-d}{a}\)
5. If α and β are the zeroes; then quadratic polynomial will be given by K[x2 – Sx + P]
where
S = α +β
P = αβ
K (≠0) is real.
6. The cubic polynomial with zeroes α, β and γ is given by
K[x3 – S1x2 + S1x2 S3]
where
S1 = α + β + γ
S2 = αβ + βγ + αγ
S3= αβγ
K(≠ 0) is real.
Degree of a Polynomial:
1. The degree of a polynomial p(x) in x is the highest power of x in p(x)
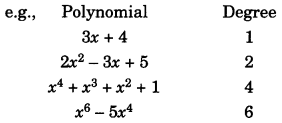
Note: Expressions like \(\frac{1}{\sqrt{x}}, \frac{1}{x^{2}+1}, \sqrt{x+2}\)
2. (i) Polynomial with degree 1, i.e., polynomial of the form ax + b; a ≠ 0 is called linear polynomial.
(ii) Polynomial with degree 2, i.e., polynomial of the form ax2 + bx + c; a ≠ 0 is called quadratic polynomial.
(iii) Polynomial with degree 3, i.e. polynomial of the form ax3 + bx2 + cx + d ; a ≠ 0 is called cubic polynomial.
(iv) Polynomial with degree 4, i.e. polynomial of the form ax4 + bx3 + cx2 + dx + e; a ≠ 0 is called biquadratic polynomial.
Geometrical Meaning of the Zeroes of a Polynomial:
1. For any polynomial y = f(x), the number of points on which the graph of y = f(x) intersects at x-axis is called the number of the zeroes of the polynomial and the x-coordinates of these points are called the zeroes of the polynomial y = f(x).
2. Polynomial with degree ‘n’ has maximum ‘n’ number of zeroes. A constant polynomial has no zeroes.
3. Geometrical representation of a linear polynomial is always a straight line.
4. Geometrical representation of a quadratic polynomial is the graph of the shape either open upwards like ‘∪’ or open downwards like ‘∩’ according to a > 0 or a < 0. These curves are called Parabola.
Relationship Between Zeroes and Coefficient of a Quadratic Polynomial:
1. If α and β are the zeroes of the quadratic polynomial p(x) = ax2 + bx + c a≠0 then
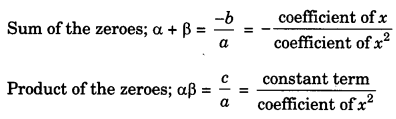
Relationship Between Zeroes and Coefficient of a Cubic Polynomial
1. If α, β and γ are the zeroes of the cubic polynomial
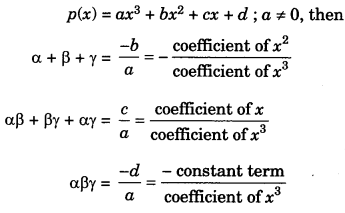
2. A quadratic polynomial p(x) with zeroes α and β is given by
p(x) = K[x2 – (α + β)x + αβ]
where K(≠0) is real.
3. A cubic polynomial p(x) with α, β and γ as zeroes is given by
p(x) = K[x3 – (α + β + γ)x2 + (αβ +βγ + αγ)x – αβγ
where K(≠0) is real.
Division Algorithm for Polynomials:
If p(x) and g(x) are any two polynomials where g(x) ≠ 0. Then on dividing p(x) by g(x), we find other two polynomials q(x) and r(x) such that
p(x) = g(x) x q(x) + r(x);
where deg. of r(x) < deg. of gix)
or Dividend = Divisor x Quotient + Remainder
Note:
- If r(x) = 0, then g(x) will be a factor of p(x) otherwise not.
- If any real number ‘a’ is a zero of the polynomial p(x), then (x – a) will be a factor of p(x).