Students rely on Class 6 Maths Extra Questions Chapter 6 Perimeter and Area Class 6 Extra Questions and Answers to improve their grades.
Class 6 Maths Chapter 6 Extra Questions Perimeter and Area
Class 6 Maths Perimeter and Area Extra Questions
NCERT Class 6 Maths Chapter 6 Perimeter and Area Extra Questions and Answers
Very Short Answer Type Questions
Question 1.
Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40 cm. Find its length and width.
Answer:
Let width of rectangle (b) = x cm
Then, length of rectangle (l) = 3x cm
Perimeter = 2(l + b)
⇒ 40 = 2 (3x + x)
⇒ 8x = 40
⇒ x = \(\frac{40}{8}\) = 5 cm
Hence, the length is 15 cm and width is 5 cm.
Question 2.
The perimeter of a regular pentagon is 1240 cm. How long is its each side?
Answer:
Given, perimeter = 1240 cm
Perimeter of a regular pentagon = 5 × Length of each side
Length of each side = \(\frac{1240}{5}\) = 248 cm
Hence, its each side is 248 cm.
Question 3.
Find the side of an equilateral triangle, if its perimeter is 30 cm.
Answer:
Given that perimeter of an equilateral triangle = 30 cm
Perimeter of an equilateral triangle
= 3 × Side of a triangle
⇒ 30 = 3 × Side of a triangle
⇒ Side = \(\frac{1}{2}\) = 10 cm
Hence, the side of an equilateral triangle is 10 cm.
![]()
Question 4.
Find the perimeter of a triangle, whose three sides are 5 cm, 6 cm and 7 cm, respectively.
Answer:
Perimeter of a triangle = Sum of its all sides
= a + b + c
= (5 + 6 + 7) cm
= 18 cm
Question 5.
Find the perimeter of an equilateral triangle, whose each side is 5 cm.
Answer:
Perimeter of an equilateral triangle = 3 × Side of length
= 3 × 5 cm
= 15 cm
Question 6.
Find the side of an equilateral triangle, whose perimeter is 27 cm.
Answer:
Given, perimeter of an equilateral triangle = 27 cm
We know that equilateral triangle has all the three sides are equal.
Side of equilateral triangle = \(\frac{\text { Perimeter }}{3}\)
= \(\frac{27}{3}\) = 9 cm 3
Question 7.
Find the area of a rectangle whose length and width are 10 cm and 6 cm, respectively.
Answer:
Given that length (Z) = 10 cm
and width (b) = 6 cm
∴ Area of a rectangle = l × b
= 10 × 6
= 60 cm²
Question 8.
If the area of a square is 36 cm2, then find its perimeter.
Answer:
Given, area of a square = 36 cm2
Area = Side × Side
⇒ 36 = Side × Side
⇒ Side × Side =6×6
⇒ Side = 6 cm
Perimeter of a square = 4 × Side
= 4 × 6= 24 cm
Question 9.
By splitting the following figure into rectangles, find their area (the measures are given in metres).

Answer:
Let the given figure be divided into rectangle A and rectangle B.
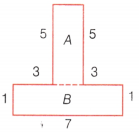
For rectangle A, length = 5 m
and breadth = 7 – (3 + 3) = 1 m
Area of rectangle A = 5 m × 1 m = 5 sq. m
For rectangle B,
length = 7 m
and breadth = 1 m
∴ Area of rectangle B = 7 × 1
= 7 sq. m
Total area of the given figure
= Area of rectangle A + Area of rectangle B = 5 + 7 = 12sq. m
Short Answer Type Questions
Question 1.
The length of a rectangular field is twice its breadth. Jamal jogged around it four times and covered a distance of 6 km. What is the length of the field?
Answer:
Let breadth of rectangular field = x m
Then, length of rectangular field = 2x m
Distance covered in one round = Perimeter
Distance covered in four rounds = 4 × Perimeter
⇒ 4 × 2(l + b) = 6 × 1000
[v perimeter =2 (l + b) and 1 km = 1000 m]
⇒ 8 (l + b) = 6000
8 (2x + x) = 6000
x = \(\frac{6000}{24}\) = 250 m
∴ Length of the field = 500 m
![]()
Question 2.
A room is 9.5 m long and 7.4 m wide. A person wants that the floor of the room to be fitted with tiles of size 20 cm by 10 cm. Find the number of tiles needed.
Answer:
Area of room = 7.4 × 9.5 m² = 7.4 × 9.5 × 10000 cm²
Area of one tile = 20 × 10 = 200 cm²
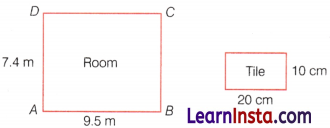
Number of tiles = \(\frac{\text { Area of room }}{\text { Area of a tile }}=\frac{74 \times 95 \times 100}{200}\)
= \(\frac{74 \times 95}{2}\) = 95 × 37 = 3515
Question 3.
Two plots of land having the same perimeter. One is a square with side 70 cm while other is rectangle of length 100 cm. Which plot has the greater area and by how much?
Answer:
Area of square = Side × Side = 70 × 70 sq cm
= 4900 cm² …(i)
Given, length of rectangle = 100 cm
Perimeter of rectangle = Perimeter of square
⇒ 2 (100 + b) = 4 × 70
⇒ 100 + b = 140
⇒ h = 40 cm
Now, area of rectangle = l × b = 40 × 100= 4000 cm²
Hence, the area of square is more than the area of rectangle by 900 cm².
Question 4.
Three squares are joined together as shown in figure. Their sides are 4 cm, 10 cm and 3 cm. Find the perimeter of the figure.

Answer:
Given, sides of three squares are 4 cm, 10 cm and 3 cm, respectively.
Total perimeter of given squares
= Sum of all outer sides of the figure
= 4 + 4 + 4 + 6 + 10 + 7 + 3 + 3 + 3 + 10
= 54 cm
Question 5.
Tahir measured the distance around a squared field as 200 rods (lathi). Later he found that the length of this rod was 140 cm. Find the side of this field in metres.
Answer:
Distance around a square field = 200 rods
Length of this rod = 140 cm
Total distance around a squared field = 200 × 140 = 28000 cm
So, perimeter of this squared field
= 28000 cm = 280 m
Sides of this field = \(\frac{280}{4}\) = 70 m
Question 6.
The perimeter of rectangle and square are equal. If length of the rectangle is 8 m and breadth is 6 m. Find the area of square.
Answer:
Given, length of rectangle (l) = 8 m
and breadth of rectangle (b) = 6 m
Perimeter of rectangle = Perimeter of square
2 (l + b) = 4 x Side of a square
⇒ 2 (8 + 6) = 4 x Side of a square
Side of a square = \(\frac{2(8+6)}{4}\) = 7 m
Area of square = 7 × 7= 49 m²
Question 7.
The floor of a room is square in shape. If the side of the floor is 5 m. Find the area of the floor.
Answer:
Given, side of the floor = 5 m
Area of the floor = Side × Side = 5 × 5 = 25 m²
Hence, the area of the floor is 25 m².
Question 8.
From the following figure, find its
(i) perimeter
(ii) area of square
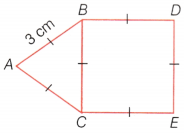
Given, ABC is an equilateral triangle of side 3 cm each and BCEDis a square.
Answer:
(i) Perimeter = AB + AC + BC + BD + DE + CE
= 3 + 3 + 3 + 3 + 3 + 3 = 18 cm
(ii) Area of square BCED = Side² = 3² = 9 cm²
Question 9.
A rectangular coconut grove is 200 m long and 50 m wide. If each coconut tree requires 20 sq. m, then what is the maximum number of tree that cap be planted in this grove?
Answer:
We have, length of the rectangular coconut grove
= 200 m and width = 50 m.
Area of the coconut grove = Length × Width
= 200 m × 50 m
= 10000 sq. m
∵ Area required by each coconut tree = 20 sq. m
To find the maximum number of tree, divide the total area by the area needed for each tree.
∴ Number of tree = \(\frac{10000 \mathrm{sq} \cdot \mathrm{~m}}{20 \mathrm{sq} \cdot \mathrm{~m}}\) = 500 trees
20 sq. m
Long Answer Type Questions
Question 1.
Length of a rectangular field is 250 m and width is 150 m. Anuradha runs around this field 3 times. How far did she run? How many times she should run around the field to cover a distance of 4 km?
Answer:
Given, length of rectangular field (Z) is 250 m and width is 150 m.
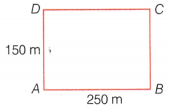
Perimeter of this field =2(l + b) = 2 (250 + 150) m
= 2 × 400 m= 800 m
Distance covered in one round = Perimeter = 800 m
Distance covered in three rounds = 3 × 800= 2400 m
Now, number of rounds to cover 4 km i.e. 4000 m.
= \(\frac{4000}{800}\) = 5 [∵ 1 km = 1000 m]
Hence, she should run 5 times around the field to cover the distance of 4 km.
![]()
Question 2.
The lawn in front of Molly’s house is 12 m × 8m, whereas the lawn in front of Dolly’s house is 15 m × 5 m. A bamboo fencing is built around both the lawns. How much fencing is required for both?
Answer:
Given, size of lawn in front of Molly’s house = 12 m × 8 m Perimeter = 2 (12 + 8) = 40 m …(i)
Now, size of lawn in front of Dolly’s house = 15 m × 5 m Perimeter = 2 (15 + 5) = 40 m .. .(ii)
From Eqs. (i) and (ii), we get 40 + 40 = 80 m
Hence, the total length of bamboo fencing required is 80 m.
Question 3.
A room 9.68 m long and 6.2 m wide. Its floor is to be covered with glazed tiles of 22 cm by 10 cm each. If rate of tiles is ₹ 25 per tile. Find the total cost of tiles.
Answer:
Given, length of floor of the room (l) = 9.68 m
and width of floor of the room (b) = 6.2 m
Area of the room = 9.68 × 6.2 m² …(i)
Also, given that length of each tile = 22 cm
and width of each tile =10 cm
Now, area of each tile = 22 × 10 cm² … (ii)
Number of tiles required to cover the floor of the room [vl m= 100 cm]
= 2728
∴ Total cost = ₹ 2728 × 25 = ₹ 68200
Question 4.
There is a rectangular lawn 10 m long and 4 m wide in 6. In the given figure, all triangles are equilateral and front of Meena’s house. It is fenced along the two AB = 8 units. Other triangles have been formed by smaller sides and one longer side leaving a gap of 1 m taking the mid-points of the sides. What is the for the entrance. Find the length of fencing. perimeter of the figure?

Answer:Given, width of the lawn, AB = EF = 4 m
and length of the lawn, BE = 10 m
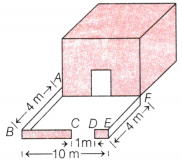
Also, given length of gap, CD = 1 m
Total length of fencing = AB + (BC + DE)+ EF
= AB + (BE – CD) + EF
= 4 + (10 – 1) + 4
= 4 + 9 + 4
= 17m
Hence, the length of fencing of the lawn is 17 m.
Question 5.
Observe these two figures. Is there any similarity or difference between the two?
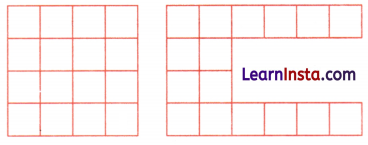
Using 16 units square (having an area of 16 sq. units) We have made figures with two different perimeters. The first,figure has a perimeter of 16 units and second has perimeter of 28 units.
Using 16 units square, answer the following questions.
(i) What is the smallest perimeter possible?
(ii) What is the largest perimeter possible?
(iii) Make a figure with perimeter of 18 units.
(iv) Can you make other shaped figures for each of the above three perimeters or is there only one shape with that perimeter? What is your reasoning?
Answer:
(i) The smallest perimeter possible using 16 units square is 16 units when arranged in a 4 × 4 squares.
(ii) The largest perimeter possible using 16 Unit squares is 34 units when arranged in a straight line of 1 × 16 square.
(iii) A possible figure with a perimeter of 18 units can be arranged in a 2 × 7 rectangle as given below.
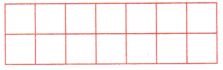
(iv) Yes, different shaped figure can have the same perimeter. The perimeter depends on the arrangement of the square and not just the number of square.
Question 6.
In the given figure, all triangles are equilateral and AB = 8 units. Other triangles have been formed by taking the mid-points of the sides. What is the perimeter of the figure?
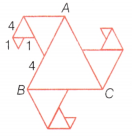
Answer:
Given, ∆ABC is an equilateral triangle.
Here, AB = 8 units
AB = BC = CA = 8 units
Now, ∆ADE is an equilateral triangle.
Here, E is the mid-point of AB.
AE = BE = \(\frac{A B}{2}=\frac{8}{2}\) = 4 units
Now, in ∆ADE, AD = DE = EA = 4 units
Similarly, equilateral triangles are ∆BOT and ∆UPC, having each sides equal
i.e. BO = OT = BT = UC = PC = PU = 4 units
It is also clear that OC = PA = 4 units
Also, ∆DIF is an equilateral triangle.
Here, F is the mid-point of DE.
DF = FE = \(\frac{D E}{2}=\frac{4}{2}\) = 2 units
In ∆DIF, DI = IF = DF = 2 units
Similarly, in ∆TKN and ∆RQU,
TK = KN = TN = RQ = UQ = UR = 2 units
It is also clear that NO = RP = 2 units
Also, ∆HIG is an equilateral triangle.
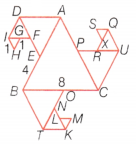
Here, G is the mid-point of IF.
IG = GF = \(\frac{I F}{2}=\frac{2}{2}\) = 1 unit 2 2
Now, in ∆HIG, HG = HI = GI=1 unit
Similarly, in ∆MLK and ∆XQS,
ML = MK = LK = SQ = XS = QX =1 unit
It is also clear that LN = XR = 1 unit
Now, perimeter of the given figure
= Sum of all outer sides of the given figure = AD+DI + IH + HG + GF + FE + EB + BT +TK + KM + LM + LN + NO + OC +CU + UQ + QS + XS + XR + PR + PA
= [4 + 2 + 1 + 1 + 1 + 2 + 4 + 44 – 2 + 1 + 1 + 14 – 2 + 4 + 4 + 2 + 1 + 1 + 1 + 2 + 4]
= 45 units
Hence, the perimeter of the given figure is 45 units.
Question 7.
If length of a rectangle is halved and breadth is doubled, then the area of the rectangle obtained remains same. Is it true?
Answer:
True, let the length and breadth of a rectangle be l and b respectively.
We know that
Area of the initial rectangle = Length × Breadth
= l × b sq units
If length of a rectangle is halved and breadth is doubled,
i.e. New length = \(\frac{l}{2}\) units
and new breadth = 2b units
Then, the area of new rectangle
= New length × New breadth = \(\frac{l}{2}\) × 2b
= lb sq units
Question 8.
In the given figure, each square is of unit length.

(i) What is the perimeter of the rectangle ABCD?
(ii) What is the area of the rectangle ABCD?
(iii) Divide this rectangle into ten parts of equal area by shading squares. (Two parts of equal area are shown here)
(iv) Find the perimeter of each part which you have divided. Are they all equal? Competency Based Question
Answer:
Given, each side of square is of unit length. Figure contains length of 10 squares and width of 6 squares.
Now, the length of rectangle, AD = BC
= Sum of length of a side of 10 squares = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10 × 1 = 10 units
and breadth of rectangle, AB = DC
= Width of 6 squares = 6 × 1 = 6 units
(i) The perimeter of the rectangle ABCD
= AB + BC + CD + DA = 6 + 10 + 6 + 10
= 32 units
(ii) The area of the rectangle ABCD = Length × Breadth
= AD × AB = 10 × 6
= 60 sq units
(iii) The total area of rectangle = 60 units
Now, we have to divide the rectangle into 10 equal parts i.e. \(\frac{60}{10}\) =6 squares units 10
i.e. we have to take a group of 6-6 square blocks, which is shown in the figure.
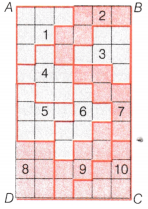
(iv) Now, we find the perimeter of Part I.
We know that perimeter of a figure is the total length of its boundary.
.’. Perimeter of Part I
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 12 units
Similarly, we can find the perimeters of remaining 9 parts, all the parts have same perimeter i.e. 12 units. Yes, all the parts have same perimeter.
![]()
Case-Based Questions
Question 1.
The figure below shows the football field for a school tournament.
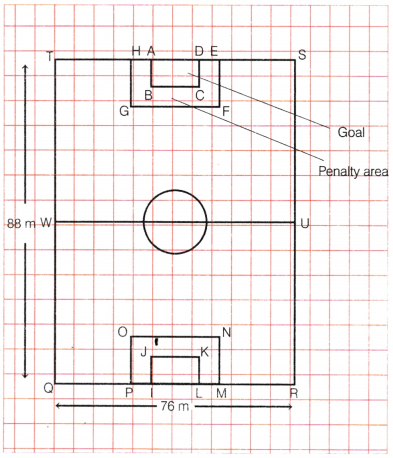
(i) What is the perimeter (in m) of WURQ?
(a) 60 m
(b) 240 m
(c) 960 m
(d) 3344 m
Answer:
(b) Given, length of the football field = 88 m
breadth of the football field = 76 m
WQ = \(\frac{1}{2}\) × TQ = \(\frac{1}{2}\) × 88 = 44 m
Now, perimeter ofWURQ = 2 × (length + breadth)
= 2 × (44 + 76)
= 2 × 120
= 240 m
Hence, perimeter of WURQ is 240 m.
(ii) The area enclosed by QRUW is equal to +he area enclosed by WUST. Is the statement true? Give reason.
Answer:
We have, TW = WQ = 44 m and QR = WU = 76 m
Now, area enclosed by QR UW = Length × Breadth
= WQ × Q.R = 44 m × 76 m = 3344 m² …(i)
Now, area enclosed by WUST = Length × Breadth
= TW × WU = 44 …(ii)
∴ From (i) and (ii);
Area enclosed by QRUW
= Area enclosed by WUST = 3344 m²
Hence, area enclosed by QRUW is equal to the area enclosed by WUST.
(iii) What is the area (in m²) of the penalty area?
(a) 488 m²
(b) 272 m²
(c) 480 m²
(d) 720 m²
Answer:
(c) Given, length of the football field = 88 m
and breadth of the football field = 76 m
∴ Side of the small square in the field = \(\frac{88}{22}\) = 4 m
∴ Area of small square in the field = 4 × 4 = 16 m²
Now, there are 30 small squares lying in the region of penalty area.
∴ Area of the penalty area = 30 × Area of small square
= 30 × 16 m²
= 480 m²
Hence, the area of penalty area is 480 m².
(iv) Is the perimeter of the penalty area of the football field double the perimeter of the goal area? Give reason.
Answer:
We have, side of small square = 4 m
∴ HG = 20 m, GF = 36 m, FE = 20 m, ED = 8 m,
DC = 12 m, CB = 20 m, BA = 12 m and AH = 8 m
Perimeter of penalty area
= HG + GF + FE + ED + DC + CB + BA + AH
= 20 + 36 + 20 + 8 + 12 + 20 +12+8 = 136 m …(i)
Now, AB = 12 m, BC = 20 m, CD = 12 m and DA = 20 m
∴ Perimeter of goal area = AB + BC + CD + DA
= 12 + 20 + 12 + 20
= 64 m
Hence, perimeter of,the penalty area of the football field is not double the perimeter of the goal area.
(v) Does the school football field meet the FIFA standards? Give reason.
Answer:
Yes, the school football field meet the FIFA standards because the areas of WUST and WURQ are the same which is 3344 m2.
(a) because the length and the width of TQRS are 88 m and 76 m respectively, which lie with in the standard range which 120 m to 90 m for length and 90 m to
45 m for width.
(b) because the perimeter of TQRS is 328 m which lies with in the standard range which is 420 m to 270 m.
(c) because the area of TQRS is 6688 sq m which lies with in the standard range which 10800 sq m to 4050 sq m.
![]()
Question 2.
Below is the house plan of Mr. Rahul. It is in a rectangular plot. Look at the plan.
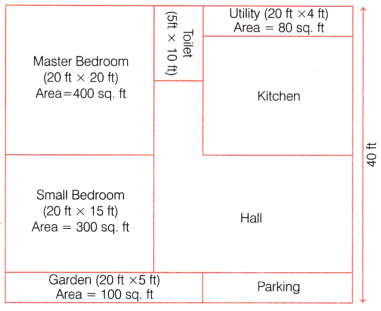
On the bases of above diagram answer the following questions.
(i) Find the perimeter of parking.
Answer:
It is clear from the given figure that width of parking and width of garden is same.
So, width of garden = 5 ft
Now, Length of parking = Length of utility = 20 ft
Hence, perimeter of parking = 2 (5 + 20) = 50 ft
(ii) Find the measure of length and width of the kitchen.
Answer:
From the diagram,
Length of kitchen = Length of utility = 20 ft
and Width of kitchen = Length of master bed – Width of utility
= 20 – 4 = 16 ft.
(iii) The area of the hall is
(a) 325 sq. ft
(b) 225 sq. ft
(c) 400 sq. ft
(d) 425 sq. ft
Answer:
(d) It is clear, length of hall = 25 ft
∴ Area of the hall = (25 × 15) sq. ft + (10 × 5) sq. ft
= 375 sq. ft + 50 sq. ft
= 425 sq. ft.
(iv) The area of whole house of Mr. Rahul is
(a) 1200 sq. ft
(b) 1008 sq. ft
(c) 1800 sq. ft
(d) 525 sq. ft
Answer:
(c) It is clear, that
length of house = 20 + 20 + 5 = 45 ft
Also, given width of house = 40 ft
∴ Area of house = Length × Width
[∵ plot is rectangular] = 45 × 40 = 1800 sq.ft
Question 3.
The figure below shows a square wooden frame enclosing a square picture.

(i) What is the area (in cm²) of the frame?
(a) 81cm²
(b) 144cm²
(c) 181cm²
(d) 225cm²
Answer:
(d) Given, side of square frame = 15 cm
Now, area of square frame = Side × Side
= 15 × 15 = 225 cm²
Hence, area of the frame is 225 cm².
(ii) What is the perimeter (in cm) of the picture?
(a) 12 cm
(b) 48 cm
(c) 60 cm
(d) 144 cm
Answer:
(b) Given, side of the square picture = 12 cm
Now, perimeter of square picture = 4 × Side
= 4 × 12 = 48 cm
Hence, perimeter of the picture is 48 cm.
Class 6 Maths Chapter 6 Extra Questions in Hindi परिमाप और क्षेत्रफल
Perimeter and Area Class 6 Extra Questions in Hindi
उदाहरण (हल सहित)
उदाहरण 1.
एक टेबल-टॉप का माप 2 m 25 cm गुणा 1m 50 cm है। टेबल-टॉप का परिमाप क्या है?
हल:
टेबल-टॉप का परिमाप

= 2 × (लंबाई + चौड़ाई)
= 2 × (2 m 25 cm + 1 m 50 cm)
= 2 × (2.25 m + 1.50 m)
= 2 × (3.75 m)
= 7.5 m
उदाहरण 2.
निम्न आकृतियों के परिमाप ज्ञात कीजिए-
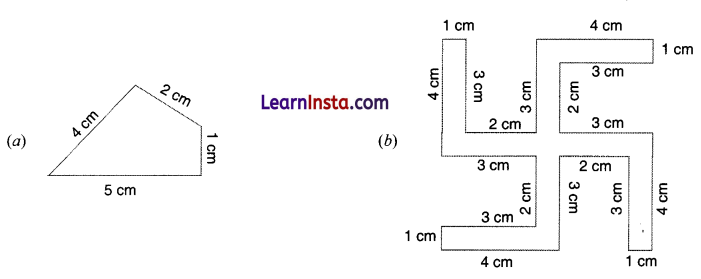
हल:
(a) परिमाप = इसकी भुजाओं की लंबाइयों का योग
= 5 cm + 1 cm + 2 cm + 4 cm = 12 cm
(b) परिमाप = इसकी भुजाओं की लंबाइयों का योग
= 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm + 4 cm + 1 cm + 3 cm +2 cm + 3 cm + 4 cm + 1 cm + 3 cm + 2 cm + 3 cm
= 10 cm + 13 cm + 13 cm + 16 cm = 52 cm
उदाहरण 3.
12 रुपये प्रति मीटर की दर से 175 m लंबाई और 125 m चौड़ाई वाले आयताकार पार्क में बाड़ लगाने का व्यय ज्ञात कीजिए।
हल:
आयताकार पार्क का परिमाप

= 2 × (लंबाई + चौड़ाई)
= 2 × (175 m + 125m )
= 2 × 300 m = 600m
∴ ₹ 12 प्रति मीटर की दर से आयताकार पार्क में बाड़ लगाने का व्यय
= 600 × ₹ 7200
![]()
उदाहरण 4.
नीचे दी गई आकृतियों के क्षेत्रफल को वर्ग गिनकर ज्ञात कीजिए-
हल:
(a)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 9 | 9 × 1 = 9 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 9 वर्ग इकाई
(b)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 5 | 5 × 1 = 5 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 5 वर्ग इकाई
(c)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 2 | 2 × 1 = 2 |
| आधा भरे वर्ग | 4 | 4 × \(\frac{1}{2}\) = 2 |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 2 + 2 = 4 वर्ग इकाई
(d)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 8 | 8 × 1 = 8 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 2 + 2 = 4 वर्ग इकाई
उदाहरण 5.
नीचे दी गई आकृतियों के क्षेत्रफल को वर्ग गिनकर ज्ञात कीजिए-

हल:
(a)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 17 | 17 × 1 = 17 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | 4 | 4 × 1 = 4 |
| आधे से कम भरे वर्ग | 6 | – |
∴ आकृति का अनुमानित कुल क्षेत्रफल = 17 + 4 = 21 वर्ग इकाई
(b)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 12 | 12 × 1 = 12 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | 6 | 6 × 1 = 6 |
| आधे से कम भरे वर्ग | 8 | – |
∴ आकृति का अनुमानित कुल क्षेत्रफल
= 12 + 6 = 18 वर्ग इकाई
उदाहरण 6.
निम्नलिखित आकृतियों के क्षेत्रफल को वर्ग गिनकर ज्ञात करें-

हल:
(a)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 2 | 2 × 1 = 2 |
| आधा भरे वर्ग | 4 | 4 × 1/2 = 2 |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 2 + 2 = 4 वर्ग इकाई
(b)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 4 | 4 × 1 = 4 |
| आधा भरे वर्ग | 4 | 4 × 1/2 = 2 |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 4 + 2 = 6 वर्ग इकाई
(c)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 5 | 5 × 1 = 5 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 5 वर्ग इकाई
(d)
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 9 | 9 × 1 = 9 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 9 वर्ग इकाई
![]()
उदाहरण 7.
निम्न आकृति के क्षेत्रफल को वर्ग गिनकर ज्ञात करें-

हल:
| घिरा क्षेत्र | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 30 | 30 × 1 = 30 |
| आधा भरे वर्ग | – | – |
| आधे से अधिक भरे वर्ग | – | – |
| आधे से कम भरे वर्ग | – | – |
∴ आकृति का कुल क्षेत्रफल = 30 वर्ग इकाई
उदाहण 8.
निम्नलिखित आकृति के क्षेत्रफल को वर्ग गिनकर ज्ञात करें:

हल:
| घिरा क्षेत्रफल | संख्या | अनुमानित क्षेत्रफल (वर्ग इकाई) |
| पूर्ण भरे वर्ग | 10 | 10 × 1 = 10 |
| आधा भरे वर्ग | 5 | 5 × 1⁄2 = 2.5 |
∴ कुल क्षेत्रफल 10 वर्ग इकाई + 2.5 वर्ग इकाई 12.5 वर्ग इकाई
परीक्षापयोगी प्रश्न
प्रश्न 1.
आयत के परिमाप का सूत्र क्या है?
(a) लंबाई × चौड़ाई
(b) लंबाई + चौड़ाई
(c) 2 × ( लंबाई + चौड़ाई)
(d) 2 × ( लंबाई × चौड़ाई)
हल:
(a) आयत का परिमाप
= लंबाई × चौड़ाई
प्रश्न 2.
आकृति का परिमाप

है
(a) 12 m
(b) 14 m
(c ) 24 m
(d) 7 m.
हलः
(b) आकृति का परिमाप
= 4 + 3 + 4 + 3 = 14 m
प्रश्न 3.
आकृति का परिमाप

(a) 5 cm
(b) 10 cm
(c ) 15 cm
(d) 20 cm
हल:
(d) आकृति का परिमाप
= 2 + 2 + 1 + 2 + 2 + 1 + 2 + 2 + 1 + 2 + 2 + 1 = 20 cm
![]()
प्रश्न 4.
त्रिभुज की दो भुजाएँ 5 cm व 4 cm हैं। त्रिभुज का परिमाप 12 cm है। त्रिभुज की तीसरी भुजा की लंबाई है
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 6 cm
हल:
(c ) त्रिभुज की तीसरी भुजा
= त्रिभुज का परिमाप – अन्य दो भुजाओं की लंबाई
= 12 – 5 – 4 = 3 cm
प्रश्न 5.
कार्डबोर्ड के आयताकार टुकड़े का परिमाप 6 m है।
इसकी चौड़ाई 1 m है। इसकी लंबाई ज्ञात कीजिए:
(a) 1 m
(b) 2 m
(c) 3 m
(d) 6 m
हल:
(a) अभीष्ट लंबाई
= \(\frac{1}{2}\) कार्डबोर्ड का परिमाप – चौड़ाई
= \(\frac{1}{2}\) – 1 = 3 – 1 = 2 m
प्रश्न 6.
एक तार का टुकड़ा 30cm लंबा है। यदि तार का उपयोग निम्नलिखित बनाने के लिए किया जाता है। तो प्रत्येक भुजा की लंबाई क्या होगी?
(a) एक वर्ग ?
(b) एक समबाहु त्रिभुज?
(c) एक सम षट्भुज?
हल:
(a) वर्ग का परिमाप
= 4 × भुजा की लंबाई
⇒ 30 = 4 × भुजा की लंबाई
⇒ भुजा की लंबाई = \(\frac{30}{4}\) = 7.5 cm
(b) समबाहु त्रिभुज का परिमाप = 3 × भुजा की लंबाई
⇒ 30 = 3 × भुजा की लंबाई
⇒ भुजा की लंबाई = \(\frac{30}{3}\) = 10 cm
(c) सम षट्भुज का परिमाप = 6 × भुजा की लंबाई
⇒ 30 = 6 × भुजा की लंबाई
⇒ भुजा की लंबाई = \(\frac{30}{6}\) = 5 cm
प्रश्न 7.
100 m लंबाई व 75 m चौड़ाई वाले एक आयताकार पार्क में ₹ 15 प्रति मीटर की दर से बाड़ लगाने की लागत ज्ञात कीजिए।
हल:
आयताकार पार्क का परिमाप
= 2 × (लंबाई × चौड़ाई)
= 2 × (100 m + 75 m)
= 2 × 175 m = 350 m
∴ ₹ 15 प्रति मीटर की दर से बाड़ लगाने की लागत
= 350 × ₹ 5250
प्रश्न 8.
स्वीटी 75 m भुजा वाले एक वर्गाकार पार्क के चारों ओर दौड़ती है। बुलबुल 60 m लंबाई व 45 m चौड़ाई वाले एक आयताकार पार्क के चारों ओर दौड़ती है। किसने कम दूरी तय की?
हल:
वर्गाकार पार्क का परिमाप
= 4 × भुजा की लंबाई
= 4 × (75 m)
= 300 m
आयताकार पार्क का परिमाप
= 2 × (लंबाई + चौड़ाई)
= 2 × (60 m + 45 m )
= 2 × (105 m)
= 210 m
चूँकि आयताकार पार्क का परिमाप वर्गाकार पार्क के परिमाप से कम है। इसलिए बुलबुल ने कम दूरी तय की।
![]()
प्रश्न 9.
निम्नलिखित आकृतियों में से प्रत्येक का परिमाप क्या है ? उत्तरों से आप क्या निष्कर्ष निकालते हैं?
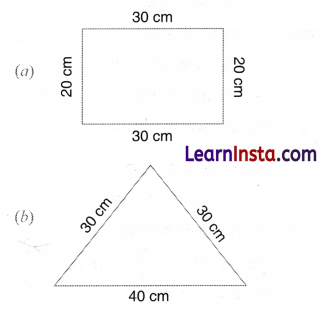
हल:
(a) आकृति का परिमाप
= सभी भुजाओं की लंबाइयों का योग
= 30 cm + 20 cm + 30 cm + 20 cm
= 100 cm
(b) आकृति का परिमाप
= सभी भुजाओं की लंबाइयों का योग
= 40 cm + 30 cm + 30 cm
= 100 cm
उत्तरों से हम यह निष्कर्ष निकालते हैं कि दोनों आकृतियों का परिमाप समान हैं।
प्रश्न 10.
एक वर्गाकार मैदान की प्रत्येक भुजा की माप 25 m है। इस मैदान से लगा हुआ एक आयताकार मैदान है जिसकी भुजाओं का अनुपात 3:2 है। यदि दोनों मैदानों का परिमाप समान हैं तब आयताकार मैदान की भुजाएँ ज्ञात कीजिए।
हल:
वर्गाकार मैदान का परिमाप
= 4 × एक भुजा की लंबाई
= 4 × 25 m
= 100 m
माना आयताकार मैदान की लंबाई व चौड़ाई क्रमशः 3x m और 4x m है
तब आयताकार मैदान का परिमाप
= 2 × (लंबाई + चौड़ाई)
= 2 × (3x m + 2x m)
= 2 × (5x m)
= 10x m
प्रश्नानुसार,
आयताकार मैदान का परिमाप = वर्गाकार मैदान का परिमाप
⇒ 10x = 100
⇒ x = \(\frac{1}{2}\) = 10
∴ आयताकार मैदान की लंबाई
3x = 3 × 10 = 30 m
आयताकार मैदान की चौड़ाई
2x = 2 × 10 = 20 m
अतः आयताकार मैदान की भुजाएँ क्रमश: 30 m और 20 m हैं।
I. बहुविकल्पीय प्रश्न
प्रश्न 1.
निम्नलिखित आकृतियाँ छह इकाई वर्गों को मिलाकर बनाई गई हैं। किस आकृति का परिमाप न्यूनतम है? (NCERT दिग्दर्शिका)

(a) (ii)
(b) (iii)
(c) (iv)
(d) (i)
उत्तर:
(d) (i)
प्रश्न 2.
100 मीटर भुजा वाले एक वर्गाकार पार्क ABCD में दो बराबर आयताकार फूलों की क्यारियाँ हैं, जिनमें से प्रत्येक का आकार 10 मीटर × 5 मीटर है (चित्र देखें)। शेष पार्क की सीमा की लंबाई है (NCERT दिग्दर्शिका)

(a) 360 m
(b) 400 m
(c) 340 m
(d) 460 m
उत्तर:
(b) 400 m
प्रश्न 3.
वर्ग का परिमाप =
(a) 4 × एक भुजा की लंबाई
(b) 2 × एक भुजा की लंबाई
(c) 3 × एक भुजा की लंबाई
(d) 6 × एक भुजा की लंबाई
उत्तर:
(a) 4 × एक भुजा की लंबाई
प्रश्न 4.
समबाहु त्रिभुज का परिमाप =
(a) 2 × एक भुजा की लंबाई
(b) 3 × एक भुजा की लंबाई
(c) 4 × एक भुजा की लंबाई
(d) 6 × एक भुजा की लंबाई
उत्तर:
(b) 3 × एक भुजा की लंबाई
प्रश्न 5.
आयत का क्षेत्रफल
(a) लंबाई × चौड़ाई
(b) लंबाई + चौड़ाई
(c) 2 × ( लंबाई + चौड़ाई)
(d) 2 × (लंबाई × चौड़ाई)
उत्तर:
(a) लंबाई × चौड़ाई
![]()
प्रश्न 6.
आकृति A का परिमाप

है
(a) 8 m
(b) 16 m
(c) 4 m
(d) इनमें से कोई नहीं
उत्तर:
(a) 8 m
प्रश्न 7.
आकृति का परिमाप

है-
(a) 20 cm
(b) 10 cm
(c ) 24 cm
(d) 15 cm.
उत्तर:
(a) 20 cm
प्रश्न 8.
एक धावक एक आयताकार पार्क जिसकी लंबाई 40 m और चौड़ाई 30 m है के चारो ओर 10 चक्कर लगाता है। उसके द्वारा तय की गई दूरी ज्ञात कीजिए।
(a) 1400 m
(b) 700 m
(c) 70 m
(d) 2800 m.
उत्तर:
(a) 1400 m
प्रश्न 9.
10 मीटर लंबाई और 5 मीटर चौड़ाई वाले एक आयताकार पार्क में ₹ 10 प्रति मीटर की दर से बाड़ लगाने की लागत ज्ञात कीजिए
(a) ₹ 600
(b) ₹ 300
(c) ₹ 150
(d) ₹ 1200.
उत्तर:
(b) ₹ 300
प्रश्न 10.
संगीता द्वारा तय की गई दूरी ज्ञात कीजिए यदि वह 10 मीटर भुजा वाले वर्गाकार पार्क के 5 चक्कर लगाती है।
(a) 200 m
(b) 100m
(c) 400 m
(d) 800 m.
उत्तर:
(a) 200 m
प्रश्न 11.
आकृति का परिमाप

है-
(a) 15 cm
(b) 20 cm
(c) 10 cm
(d) 50 cm.
उत्तर:
(c) 10 cm
![]()
प्रश्न 12.
2 सेमी, 3 सेमी और 4 सेमी भुजाओं वाले त्रिभुज का परिमाप है-
(a) 9 cm
(b) 18 cm
(c ) 27 cm
(d) 36 cm.
उत्तर:
(a) 9 cm
प्रश्न 13.
एक त्रिभुज की दो भुजाएँ 5 सेमी और 4 सेमी हैं। त्रिभुज का परिमाप 12 सेमी है। तीसरी भुजा की लंबाई है-
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 6 cm.
उत्तर:
(c) 3 cm
प्रश्न 14.
2 सेमी लंबाई और 1 सेमी चौड़ाई वाले एक आयत का क्षेत्रफल है-
(a) 1 cm2
(b) 2 cm2
(c) 4 cm2
(d) 8 cm2
उत्तर:
(b) 2 cm2
प्रश्न 15.
1 सेमी भुजा वाले वर्ग का क्षेत्रफल है-
(a) 1 cm2
(b) 4 cm2
(c) 9 cm2
(d) 16 cm2
उत्तर:
(a) 1 cm2
प्रश्न 16.
कागज़ की एक आयताकार शीट का क्षेत्रफल 20 सेमी2 है। इसकी लंबाई 5 सेमी है। इसकी चौड़ाई ज्ञात कीजिए।
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm.
उत्तर:
(d) 4 cm.
II. मिलान करें
कॉलम I में दी गई आकृतियों (प्रत्येक भुजा की माप 2 सेमी है) का कॉलम II में दिए गए संगत परिमापों से मिलान करें-
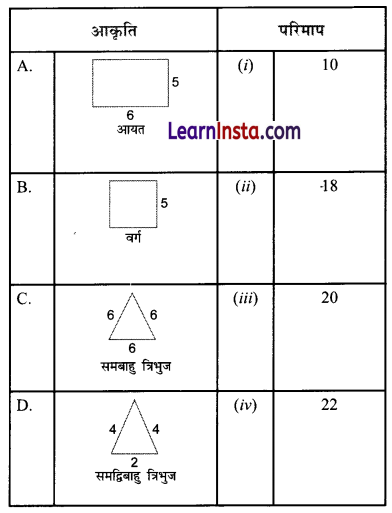
उत्तर:
A. (iv)
B. (iii)
C. (ii)
D. (i)
III. लघु उत्तरीय प्रश्न
प्रश्न 1.
40 सेमी × 10 सेमी भुजा वाले एक आयताकार बॉक्स के ढक्कन को चारों ओर से टेप से सील कर दिया गया। है। आवश्यक टेप की लंबाई क्या है?
उत्तर:
100 cm
प्रश्न 2.
निम्नलिखित आकृतियों में से प्रत्येक का परिमाप ज्ञात कीजिए-
(a) 9 सेमी, 4 सेमी और 5 सेमी भुजाओं वाला एक त्रिभुज
(b) 3 सेमी वाला एक समबाहु त्रिभुज
(c) एक समद्विबाहु त्रिभुज जिसमें समान भुजाएँ 8 सेमी और तीसरी भुजा 6 सेमी है।
उत्तर:
(a) 12 cm
(b) 27 cm
(c) 22 cm
प्रश्न 3.
उस वर्ग की भुजा ज्ञात कीजिए जिसका परिमाप 20 मीटर है।
उत्तर:
5 m
![]()
प्रश्न 4.
एक त्रिभुज की दो भुजाएँ 12 सेमी और 14 सेमी हैं। त्रिभुज का परिमाप 36 सेमी है। इसकी तीसरी भुजा क्या है?
उत्तर:
10 cm
प्रश्न 5.
उन आयतों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएँ हैं-
(a) 3 cm और 4 cm
(b) 12 m और 21 m
उत्तर:
(a) 12 sq. cm
(b) 252 sq. cm
प्रश्न 6.
उन वर्गों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएँ हैं-
(a) 14 cm
(b) 5 m.
उत्तर:
(a) 196 sq. m
(b) 25 sq. cm
प्रश्न 7.
एक कमरा 4 मीटर लंबा और 3 मीटर 50 सेमी चौड़ा है। कमरे के फर्श को ढकने के लिए कितने वर्ग मीटर कालीन की आवश्यकता होगी?
उत्तर:
14 sq. m
प्रश्न 8.
एक टेबल-टॉप का माप 2 मीटर × 1 मीटर 50 सेमी है। इसका क्षेत्रफल वर्ग मीटर में कितना है?
उत्तर:
3 sq. m