MCQ on Number Play Class 6
Class 6 Maths Chapter 3 MCQ Number Play
Multiple Choice Questions
Question 1.
The greatest 5-digit number using the digit 3, 1, 0:
(a) 10003
(b) 33310
(c) 33333
(d) 33301
Answer:
(b) 33310
Question 2.
The 5-digit palindrome number using the digits 2, 5, 4 is
(a) 22254
(b) 55542
(c) 25452
(d) 44522
Answer:
(c) 25452
![]()
Question 3.
Which of the following is the smallest three digit number that does not change even if the digits are written in reverse order?
(a) 110
(b) 101
(c) 330
(d) 909
Answer:
(b) 101
Question 4.
The sum of the smallest and largest 2-digit palindrome is:
(a) 88
(b) 90
(c) 101
(d) 110
Answer:
(d) 110
Question 5.
Which number is known as Kapreka’s magic number?
(a) 1234
(b) 4321
(c) 6174
(d) 9999
Answer:
Option (c) is correct.
Explanation:
Kaprekar’s magic number is 6174 known for its unique properties in the Kapreka routine.
Question 6.
What is the main property of palindromic numbers?
(a) They are divisible by 10.
(b) They read the same forwards and backwards.
(c) They have no repeated digits.
(d) They are always even.
Answer:
Option (b) is correct
Explanation:
Palindromic numbers read the same forwards and backwards, such as 121 and 1331.
Question 7.
In the game The 21 Game,” what is the winning number?
(a) 10
(b) 21
(c) 50
(d) 100
Answer:
Option (b) is correct
Explanation:
The goal of the “21 Game” is to be the player who says the number 21.
Question 8.
On a number line, which pattern represents numbers increasing by a fixed amount?
(a) Even and odd numbers
(b) Prime numbers
(c) Square numbers
(d) Equal intervals
Answer:
Option (d) is correct.
Explanation:
Equal intervals on a number line represent a sequence of numbers increasing by a fixed amount.
Question 9.
Which of the following is NOT a method of estimation mentioned in the chapter?
(a) Rounding numbers
(b) Using compatible numbers
(c) Finding exact values
(d) Estimating with simple averages
Answer:
Option (c) is correct.
The Chapter mentions rounding numbers, using compatible numbers and estimating with simple averages, but not finding exact values.
Question 10.
True or False: The Collate Conjecture states that the sequence will eventually reach 1.
Answer:
True
Explanation:
The Collate Conjecture suggests that will any positive integer will eventually reach 1 through the specified process.
Question 11.
True or False: The Kaprekar routine always leads to a number different from 6174.
Answer:
False
Explanation:
The Kaprekar rout.ne always leads to the number 6174, regardless of the starting number.
Question 12.
Assertion: Palindromic patterns in number are symmetrical.
Reason: A number is called palindromic if it reads the same forwards and backwards
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true But R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
Answer:
Option (a) is correct.
Explanation:
Palindromic numbers are symmetrical because they read the same forwards and backwards, which directly explains the Assertion. Hence, reason is a correct explanation for assertion.
Question 13.
Assertion: In the game ‘The 99 Game,” players add numbers between 1 and 10.
Reason: The player who says the number 99 wins the game.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true But R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
Answer:
Option (a) is correct
Explanation:
The game involves adding numbers between 1 and 10, and the player who reaches 99 wins, making the Reason a correct explanation for the Assertion.
Question 14.
Assertion: The digit sum of a number can help in determining its divisibility bv 9.
Reason: If the digit sum is divisible by 9, the original number is also divisible by 9.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true But R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
Answer:
Option (a) is correct
Explanation: If the digit sum of a number is d1visible by 9, then the original number ¡s also divisible by which explains the Assertion.
Choose the correct answer for each of the following:
(i) The smaller number whose digit sum is 15 is __________ [960000/000015]
Answer:
9,60,000
(ii) 25,000 + 400 × 2 + 13,000 + 400 ÷ 2 = ________ [38,000/39,000]
Answer:
39,000
Fill in the blanks:
(i) Write the smallest digit in the blank space, so that the digit sum is an even number.
(a) 1111__
(b) 4443__
Answer:
(a) 0
(b) 1
(ii) Total number of 4-digit numbers is _____________
Answer:
9000
Fun Activity
Complete the following crossword puzzle:
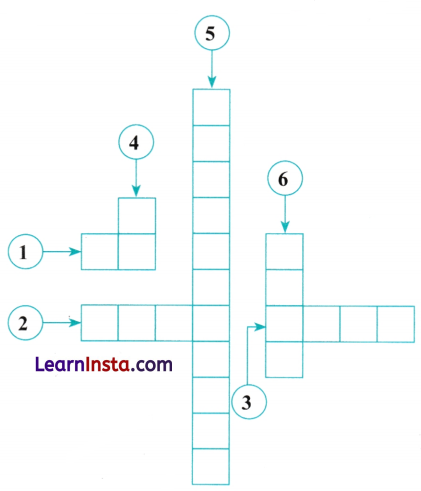
Directions:
Across:
(1) Digit sum of 154 is _____________
(2) The Kaprekar constant is based on ________ digit number.
(3) The Kaprekar constant is the number _____________
Down:
(4) How many numbers have 2-digit?
(5) When we read the number from left to right or right to left we get the same number. This type of number is called _____________ number.
(6) The difference between the greatest and the smallest number using the digit 0, 6, 3, 9, _____________
Answer:
Across
(1) 10
(2) Four
(3) 6174
Down
(4) 90
(5) Palindromic
(6) 6561
![]()
Puzzle
I am a 4-digit palindromic number,
My ten’s digit is 3 more than my thousand’s digit,
My digit sum is 22.
What number am I?
Answer:
4774
Answer the following.
Question 1.
Colour or mark the supercells in the table below.
| 596 | 451 | 265 | 104 | 105 | 106 | 107 | 109 | 108 | 210 |
Answer:
| 596 | 451 | 265 | 104 | 105 | 106 | 107 | 109 | 108 | 210 |
Question 2.
Complete the given table with 5-digit numbers whose digits are ‘1’, ‘0’, ‘4’, ‘3’, and ‘8’ in some order.
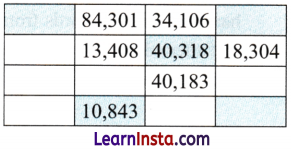
Only a shaded cell should have a number greater than all its neighbours.
Answer:
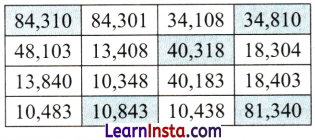
(i) The biggest number in the table is _____________
Answer:
84,310
(ii) The smallest odd number in the table is _____________
Answer:
10,483
(iii) The greatest number smaller than 50,000 in the table is _____________
Answer:
48,103
Question 3.
What is the smallest number whose digit sum is 11?
Answer:
29
Question 4.
Which number is called Kaprekar constant?
Answer:
6174
![]()
Question 5.
State which number is in left, middle and right on number line.
(i) 123, 234, 111
Answer:
Left – 111
Middle – 123
Right – 234
(ii) 10, 005; 10, 000; 00002
Answer:
Left – 00002
Middle – 10,000
Right – 10,005
Question 6.
Identify the numbers marked on the number lines below, and label the remaining positions.
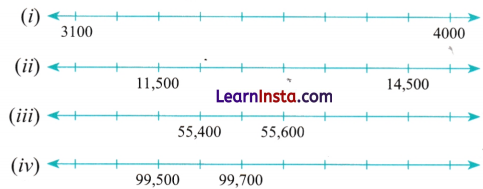
Question 7.
Case-Based Question
Ankit and Sumit are playing different games based on number theory with a set of number cards having numbers 0 to 9.

Both of them have to pick 5 different cards each from the set of cards to make a number.
Based on this information answer the following questions:
(a) If Ankit makes a 5-digit number using his cards as follows:

And Sumit placed four of his cards as follows:

At which place Sumit place his remaining card so that he can make the greater number than Ankit?
Answer:
Remaining card of number 4
40579 > 31268
![]()
(b) If Sumit wants to select the 5 number cards that make the smallest number, whose digit sum is 22, then which number card will he choose?
Answer:
0, 1, 4, 8, 9; 10489
(c) If Ankit wants to select the 5 number cards that make the greatest number whose digit sum is 25, which number card does he must choose?
Answer:
9, 8, 7, 1, 0; 98710