NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.1 are part of NCERT Solutions for Class 6 Maths. Here we have given NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.1.
- Understanding Elementary Shapes Class 6 Ex 5.2
- Understanding Elementary Shapes Class 6 Ex 5.3
- Understanding Elementary Shapes Class 6 Ex 5.4
- Understanding Elementary Shapes Class 6 Ex 5.5
- Understanding Elementary Shapes Class 6 Ex 5.6
- Understanding Elementary Shapes Class 6 Ex 5.7
- Understanding Elementary Shapes Class 6 Ex 5.8
- Understanding Elementary Shapes Class 6 Ex 5.9
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 6 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | Understanding Elementary Shapes |
| Exercise | Ex 5.1 |
| Number of Questions Solved | 7 |
| Category | NCERT Solutions |
NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.1
Question 1.
What is the disadvantage in comparing line segments by mere observation?
Solution :
Sometimes the difference in lengths betweenthe two line segments is not obvious. So, we are not always sure about our usual judgment.
Question 2.
Why is it better to use a divider than with a ruler, while measuring the length of a line segment?
Solution :
There may be errors due to the thickness of the ruler and angular viewing by using a ruler. These errors are eradicated by using a divider. So, it is better to use a divider, than a ruler, while measuring the length of a line segment.
Question 3.
Draw any line segment, say \(\overline { AB }\). Take any point C lying in between A and B. Measure the lengths of AB, BC and AC. Is AB = AC + CB? [Note : If A, B, C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B.]
Solution :
![]()
Length of AB = 7 cm
Length of BC = 3 cm
Length of AC = 4 cm
AC + CB = 4 cm + 3 cm = 7 cm
But AB = 7 cm
So, AB = AC A- CB.
Question 4.
If A, B, C are three points on a line such that AB = 5 cm, BC – 3 cm and AC – 8 cm, which one of them lies between the other two?
![]()
Solution :
AB + BC = AC, so, the point B lies between the point A and point C.
Question 5.
Verify, whether D is the mid-point of AG.
Solution :
AD = AB + BC + CD = 3 units
DG = OE + EF + FG = 3 units
∴ Yes ! D is the mid-point of AG.
![]()
Question 6.
If B is the mid-point of \(\overline { AC }\) and C is the mid-point of \(\overline { BD }\), where A, B, C, D lie on a straight line, say why AB = CD ?
Solution :
![]()
∴ B is the mid-point of \(\overline { AC }\)
∴ AB = BC …(1)
∴ C is the mid-point of \(\overline { BD }\)
∴ BC = CD … (2)
In view of (1) and (2), we get AB = CD.
Question 7.
Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.
Solution :
(i) AB = 3.7 cm
BC = 3 cm
AC = 3.8 cm
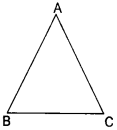
Clearly, AB + BC > AC
BC + AC > AB
AC + AB > BC
(ii) AB = 3 cm
BC = 3 cm
CA = 3 cm
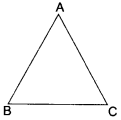
Clearly, AB + BC > AC
BC + AO AB
AC + AB > B C
(iii) AB = 4 cm
BC = 3 cm
AC = 5 cm
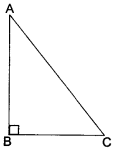
Clearly, AB + BC > AC
BC+ AC > AB
AC + AB > BC.
(iv) AB = 2 cm
BC = 2 cm
AC = 2.8 cm
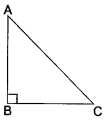
Clearly, AB + BC > AC
BC + AC > AB
AC +AB> BC
(v) AB = 3 cm
BC = 4 cm
CA = 3 cm
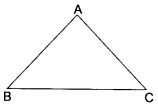
Clearly, AB + BC > AC
BC + AC> AB
AC + AB> BC
In each case, we observe that the sum of the lengths of any two sides is always greater than the third side.
We hope the NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.1 help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 5 Understanding Elementary Shapes Ex 5.1, drop a comment below and we will get back to you at the earliest.