NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.1 are part of Class 10 Maths NCERT Solutions. Here we have given NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Real Numbers |
| Exercise | Ex 1.1 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
Maths Class 10 NCERT Solutions will help you to score more marks in your CBSE board Examination.
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.1
Ex 1.1 Class 10 Question 1.
Use Euclid’s division algorithm to find the HCF of:
(i) 135 and 225
(ii) 196 and 38220
(iii) 867 and 255.
Solutions:
(i) Given numbers are 135 and 225.
On applying Euclid’s division algorithm, we have
225 = 135 x 1 + 90
Since the remainder 90 ≠ 0, so again we apply Euclid’s division algorithm to 135 and 90, to get
135 = 90 x 1 + 45
Since the remainder 45 ≠ 0, so again we apply Euclid’s division algorithm to 90 and 45, to get
90 = 45 x 2 + 0
The remainder has now become zero, so we stop.
∵ At the last stage, the divisor is 45
∴ The HCF of 135 and 225 is 45.
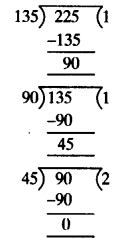
(ii) Given numbers are 196 and 38220
On applying Euclid’s division algorithm, we have
38220 = 196 x 195 + 0
Since we get the remainder zero in the first step, so we stop.
∵ At the above stage, the divisor is 196
∴ The HCF of 196 and 38220 is 196.
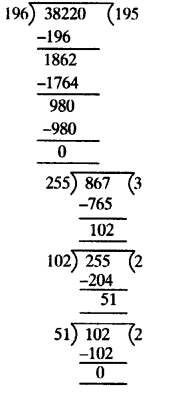
(iii) Given numbers are 867 and 255
On applying Euclid’s division algorithm, we have
867 = 255 x 3 + 102
Since the remainder 102 ≠ 0, so again we apply Euclid’s division algorithm to 255 and 102. to get
255 = 102 x 2 + 51
Since the remainder 51 ≠ 0, so again we apply Euclid’s division algorithm to 102 and 51, to get
102 = 51 x 2 + 0
We find the remainder is 0 and the divisor is 51
∴ The HCF of 867 and 255 is 51.
Exercise 1.1 Class 10 Maths NCERT Solutions Question 2.
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solutions:
Let ‘a’ be any positive integer and b = 6.
∴ By Euclid’s division algorithm, we have
a = bq + r, 0 ≤ r ≤ b
a = 6q + r, 0 ≤ r ≤ b [ ∵ b = 6] where q ≥ 0 and r = 0,1, 2, 3, 4,5
Now, ‘a’ may be of the form of 6q, 6q + 1, 6q + 2, 6q + 3, 6q + 4, 6q + 5
If ‘a’ is of the form 6q, 6q + 2, 6q + 4 then ‘a’ is an even.
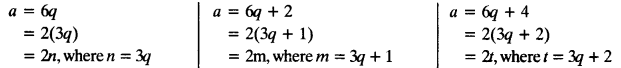
In above we can see clearly that the numbers of the form 6q, 6q + 2, 6q + 4 are having the factor 2.
∴ The numbers of the form 6q, 6q + 2, 6q + 4 are even.
If ‘a’ is of the form 6q +1,6q +3, 6q + 5 then ‘a’ is an odd.
As if
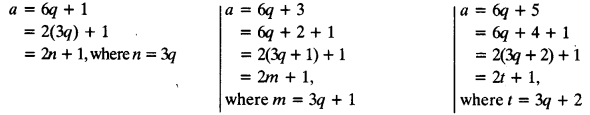
∵ We know that the number of the form 2k + 1 is odd.
∴ The numbers of the form 6q + 1, 6q + 3, 6q + 5 are odd.
Class 10 Maths Chapter 1 Question 3.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solutions:
Maximum number of columns = HCF of (616, 32)
For finding the HCF we should apply Euclid’s division algorithm
Given numbers are 616 and 32
On applying Euclid’s division algorithm, we have
616 = 32 x 19 + 8
Since the remainder 8 ≠ 0, so again we apply Euclid’s division algorithm to 32 and 8, to get
32 = 8 x 4 + 0
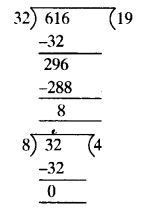
The remainder has now become zero, so we stop,
∵ At the last stage, the divisor is 8
∴ The HCF of 616 and 32 is 8.
Therefore, the maximum number of columns in which an army contingent of 616 members can march behind an army band of 32 members in a parade is 8.
Class 10 Maths Ex 1.1 Question 4.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solutions:
Let ‘a’ be any positive integer and b = 3.
∴ By Euclid’s division algorithm, we have a = 3q + r, 0 ≤ r < b
a = 3q + r, 0 ≤ r < 3 [ ∵ b = 3] where q ≥ 0 and r = 0,1, 2
∴ a = 3q or 3q + 1 or 3q + 2
Now
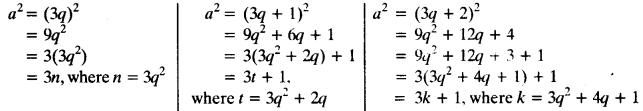
Thus, the square of any positive integer is either of the form 3m or 3m + 1.
Maths 1.1 Class 10 Question 5.
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solutions:
Let ‘a’ be any positive integer and b = 3.
∴ By Euclid’s division algorithm, we have a = bq + r,0 ≤ r ≤ b
a = 3q + r,0 ≤ r < 3 [ ∵ b = 3] where q ≥ 0 and r = 0. 1, 2
∴ a = 3q or 3q + 1 or 3q + 2
Now
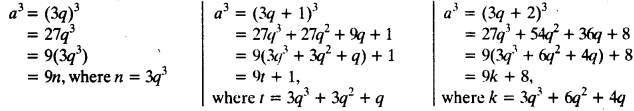
Thus, the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
We hope the NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.1 help you. If you have any query regarding NCERT Solutions for Class 10 Mathematics Chapter 1 Real Numbers Ex 1.1, drop a comment below and we will get back to you at the earliest.