Class 6 Maths Chapter 2 Lines and Angles Notes
Class 6 Maths Chapter 2 Notes – Class 6 Lines and Angles Notes
Basic Geometrical Ideas
Point
A point determines a precise location and has no length, breadth, or height. It is denoted by a single capital letter, such as P, Q, R, etc. We can mark unlimited points on a plane.
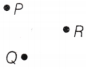
The above points will be read as points P, Q, and R.
Examples:
- The tip of a compass.
- The sharpened end of a pencil.
- The pointed end of a needle etc.
Example 1.
Tip of an ice-cream cone gives us an idea of a point. Identify such few situations in your daily life and write them.
Solution:
Such few situations in our daily life are as follows:
- The corners of a room
- Fingertip
- The location of a place on the map
- A satellite in the space
- Moon from a longer distance
![]()
Line Segment
A line segment is the shortest distance between two points. It has a definite length. The line segment joining points A and B is denoted by either \(\overline{A B}\) or \(\overline{B A}\). These points A and B are called the endpoints of the line segment AB.

Examples:
An edge of a box, a tube light, the edge of a postcard, etc.
Example 2.
Write the name of any five line segments in the following figure.
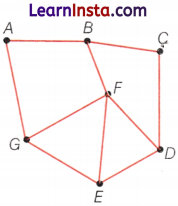
Solution:
The five line segments in the figure are \(\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}\) and \(\overline{F G}\).
Example 3.
Name the line segments in the given figure. Is P, the endpoint of each line segment?
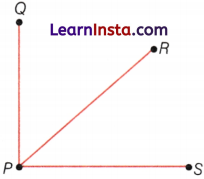
Solution:
The line segments in the given figure are as follows:
(i) \(\overline{P Q}\) (or \(\overline{Q P}\))
(ii) \(\overline{P R}\) (or \(\overline{R P}\))
(iii) \(\overline{P S}\) (or \(\overline{S R}\))
Yes, from the figure, it is clear that point P is the end point of each line segment.
Line
A line is obtained when a line segment AB is extended on both sides indefinitely. The line is denoted by \(\overleftrightarrow{A B}\). Sometimes it is also denoted by a single letter as l or m. In other words, two points are enough to fix a line. i.e. Exactly one line can be drawn through the two given points.
![]()
A line has length only. It has neither width nor thickness. An endless line can be drawn on a paper by using two arrow heads one at each end of the portion of the line which indicates that it extends in both directions indefinitely.
![]()
Example 4.
Name the line given in all possible ways, choosing only two letters at a time from the three given letters.
![]()
Solution:
The names of lines in all possible ways are as follows:
- By taking P, all possible ways are \(\overleftrightarrow{P Q}\) and \(\overleftrightarrow{P S}\).
- By taking Q, all possible ways are \(\overleftrightarrow{Q P}\) and \(\overleftrightarrow{Q S}\).
- By taking S, all possible ways are \(\overleftrightarrow{S Q}\) and \(\overleftrightarrow{S P}\).
Ray
A ray is a portion of a line that starts at a point, called a starting point or initial point, and goes in one direction endlessly.
Examples:
- Ray of light from a torch.
- Sun rays.
- Beam of light from a lighthouse, etc.

In the above figure, \(\overrightarrow{A P}\) is a ray whose starting point is A and P is a point on the path of the ray. Here, the arrow indicates that the ray \(\overrightarrow{A P}\) is endless in the direction from A to P.
Example 5.
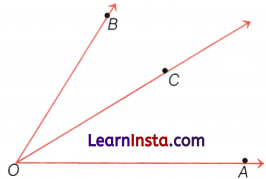
Identify the rays from the following figure.
![]()
Solution:
The rays are \(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D}, \overrightarrow{B C}, \overrightarrow{B D}\) and \(\overrightarrow{C D}\).
![]()
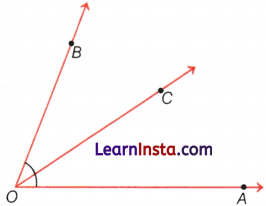
Example 6.
From the given figure answer the following.
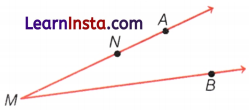
(i) Identify the rays and name them.
(ii) Is M, a starting point of each of these rays?
Solution:
(i) In the given figure, there are four rays namely \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{N A}\) and \(\overrightarrow{M B}\).
(ii) No, M is not the starting point of each of these rays. M is starting point of \(\overrightarrow{M N}\), \(\overrightarrow{M A}\), \(\overrightarrow{M B}\) and for \(\overrightarrow{N A}\), M is not the starting point.
Example 7.
In the given figure, name all the rays with initial points as P, Q, and R, respectively.

(i) Is ray \(\overrightarrow{P Q}\) different from ray \(\overrightarrow{P R}\).
(ii) Is ray \(\overrightarrow{R A}\) different from ray \(\overrightarrow{R B}\).
Solution:
\(\overrightarrow{P A}, \overrightarrow{P Q}, \overrightarrow{P R}, \overrightarrow{P B}, \overrightarrow{Q A}, \overrightarrow{Q P}, \overrightarrow{Q R}, \overrightarrow{Q B}, \overrightarrow{R A}, \overrightarrow{R P}, \overrightarrow{R Q}, \overrightarrow{R B}\), \(\overrightarrow{B R}, \overrightarrow{B Q}, \overrightarrow{B P}\), and \(\overrightarrow{B A}\).
(i) No
(ii) Yes
The distinction between a Line, a Line Segment, and a Ray
| Line | Line Segment | Ray |
| A line has no endpoint. It can be extended on both sides indefinitely. | A line segment has two endpoints. | A ray has one starting point (initial point). |
| A line cannot be drawn wholly on a paper. | A line segment can be drawn on a paper. | A ray cannot be drawn wholly on a paper. |
| A line has no definite length. | A line segment has a definite length. | A ray has no definite length. |
| \(\overleftrightarrow{A B}\) denotes a line. | The line segment is denoted by \(\overline{A B}\). | \(\overrightarrow{A B}\) represents a ray. |
| \(\overleftrightarrow{A B}\) and \(\overleftrightarrow{B A}\) represent the same line. | \(\overline{A B}\) and \(\overline{B A}\) are the same line segments. | \(\overrightarrow{A B}\) and \(\overrightarrow{B A}\) represent two different ray. |
Example 8.
By using the following figure, write
(i) all the points.
(ii) a line.
(iii) two rays with initial point Q.
(iv) two line segments.
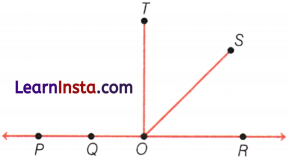
Solution:
From the given figure,
(i) all the given points are P, Q, O, R, and S.
(ii) a line is \(\overleftrightarrow{P R}\).
(iii) two rays with initial point Q is \(\overrightarrow{Q P}\) and \(\overrightarrow{Q O}\).
(iv) two line segments are \(\overrightarrow{O T}\) and \(\overrightarrow{O S}\).
Example Problems
Question 1.
With a sharp tip of the pencil, mark five points on a paper and name them by the letters A, P, Q, Y, and Z. Try to name these points in different ways.
Answer:
Do yourself.
Question 2.
Name any four line segments in the following figure.
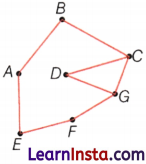
Answer:
\(\overline{A E}, \overline{B C}, \overline{A B} \text { and } \overline{D C}\)
Question 3.
Name the line segments in the given figure. Is A, the endpoint of each line segment?
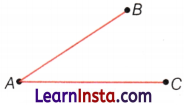
Answer:
\(\overline{A B}(\text { or } \overline{B A}), \overline{A C}(\text { or } \overline{C A})\); Yes
Question 4.
Name the line given in all possible ways, choosing only two letters at a time from the given four letters.
![]()
Answer:
\(\overleftrightarrow{M N}, \overleftrightarrow{M O}, \overleftrightarrow{M P}, \overleftrightarrow{N O}, \overleftrightarrow{N P}, \overleftrightarrow{N M}, \overleftrightarrow{O P}, \overleftrightarrow{O N}, \overleftrightarrow{O M}, \overleftrightarrow{P O}, \overleftrightarrow{P N} \text { and } \overleftrightarrow{P M}\)
Question 5.
Identify the rays from the following figure.
![]()
Answer:
\(\overrightarrow{P Q}, \overrightarrow{P R} \text { and } \overrightarrow{Q R}\)
Question 6.
(i) Name the rays in the given picture.
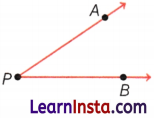
(ii) Is P, a starting point of each of these rays?
Answer:
(i) \(\overrightarrow{P A}, \overrightarrow{P B}\)
(ii) Yes
![]()
Question 7.
In the given figure, name all rays with initial points as A, B, and C respectively.

(i) Is ray \(\overrightarrow{A B}\) different from ray \(\overrightarrow{A C}\)?
(ii) Is ray \(\overrightarrow{B A}\) different from ray \(\overrightarrow{C A}\)?
(iii) Is ray \(\overrightarrow{C P}\) different from ray \(\overrightarrow{C Q}\)?
Answer:
\(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A Q}, \overrightarrow{A P}, \overrightarrow{B C}, \overrightarrow{B Q}, \overrightarrow{B A}, \overrightarrow{B P}, \overrightarrow{C Q}, \overrightarrow{C B}, \overrightarrow{C A} \text { and } \overrightarrow{C P} \text {. }\)
(i) No
(ii) Yes
(iii) No
Question 8.
Use the figure to name.
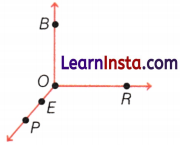
(i) Five points
(ii) Two rays
Answer:
(i) B, O, R, E, P
(ii) \(\overrightarrow{O B}, \overrightarrow{O P}\)
Question 9.
Draw a rough figure and write labels appropriately to illustrate each of the following.
(i) \(\overrightarrow{O A}\) and \(\overrightarrow{O Q}\) meet at O.
(ii) \(\overrightarrow{A B}\) and \(\overrightarrow{P Q}\) intersect at point M.
(iii) Line M contains points A and B but not point C.
(iv) Point T lies on AB.
Answer:
Do yourself.
Question 10.
Consider the following figure and answer the following with True or False.
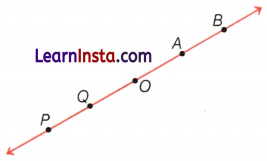
(i) Ray \(\overrightarrow{O Q}\) is not opposite to ray \(\overrightarrow{O B}\).
(ii) O is the initial point of \(\overrightarrow{O P}\).
(iii) Ray \(\overrightarrow{O P}\) is same as ray \(\overrightarrow{O B}\).
Answer:
(i) False
(ii) True
(iii) False
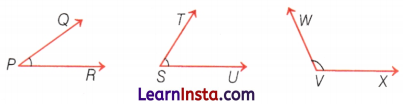
Angle
An angle is made up of two rays starting from a common starting/initial point. The two rays forming the angle are called the arms or sides of the angle and the common initial point is the vertex of the angle. In the given figure, AOB is an angle and it is denoted by ∠AOB ∠BOA or ∠O. Here, OA and OB are arrAs or sides of the angle and 0 is the vertex of the angle.
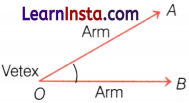
- In specifying the angle, the vertex is always written as the middle letter.
- An angle leads to three divisions of a region i.e. on the angle, the interior of the angle, and the exterior of the angle.
In this diagram, point X is in the interior of the angle. Point P, point S, and point R are on the angle, and point Y is on the exterior of the angle.
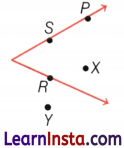
Size of Angle
The size of an angle is the amount of rotation or turn that is needed about the vertex to move the first ray to the second ray.
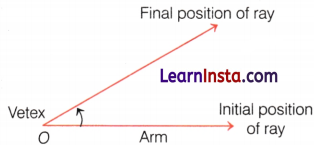
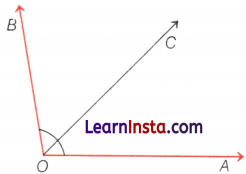
Example 1.
Write the name of the angles in the given figure.
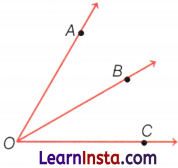
Solution:
Here, the angles are ∠AOB, ∠BOC, and ∠AOC.
Example 2.
Name the vertex and the arms of ∠PQR, given in the figure below.
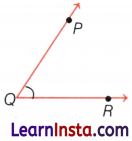
Solution:
Q is the vertex, and PQ and QR are the arms of angle ∠PQR.
Example 3.
Name the angles in the given figure.
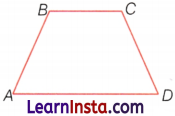
Solution:
We know that an angle is made up of two rays starting from a common initial point. So, the angles in the given figure are as follow:
(i) ∠A or ∠BAD
(ii) ∠B or ∠ABC
(iii) ∠C or ∠BCD
(iv) ∠D or ∠CDA
Example 4.
Draw rough diagrams of two angles for the conditions which are possible.
(i) One point in common.
(ii) Three points in common.
(iii) Four points in common.
Solution:
(i) In the diagram, ∠POQ and ∠ROS have point O in common.
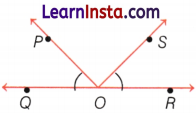
(ii) In the diagram, ∠POR and ∠ROS have points O, Q and R in common.
(iii) In the diagram, ∠POR and ∠QOR have points O, R, S and T common.
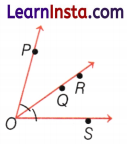
Example 5.
Draw rough diagrams of two angles such that they have one ray in common.
Solution:
Here, ∠ABC and ∠DBA have ray \(\overrightarrow{B A}\) in common.
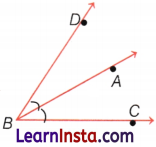
Example 6.
In the following figure, how many angles are there? Name them.
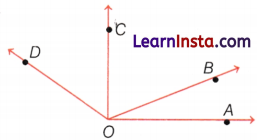
Solution:
There are 6 angles.
i.e. ∠BOA, ∠COA, ∠DOA, ∠BOC, ∠BOD and ∠COD.
![]()
Example 7.
In figure, write another name for
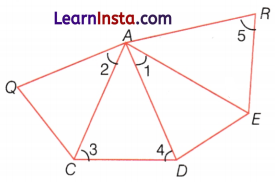
(i) ∠1
(ii) ∠2
(iii) ∠3
(iv) ∠4
(v) ∠5
Solution:
(i) ∠1 → ∠DAE or ∠EAD
(ii) ∠2 → ∠QAC or ∠CAQ
(iii) ∠3 → ∠ACD or ∠DCA
(iv) ∠4 → ∠ADC or ∠CDA
(v) ∠5 → ∠ARE or ∠ERA
Example 8.
In the given diagram, name the point(s).
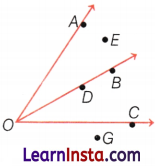
(i) In the interior of ∠AOB.
(ii) In the exterior of ∠BOC.
(iii) On ∠AOB.
Solution:
(i) In the given figure, point E lies between the sides OA and OB. So, it is in the interior of ∠AOB.
(ii) In the given figure, points E, A and G are in the exterior of ∠BOC.
(iii) In the given figure, point A, O, D and B lies on the sides OB and OA of ∠AOB, so these points are on ∠AOB.
Comparing Angles
Any two angles can be compared by placing them one over the other i.e. by superimposition. During superimposing, the vertices of the angles must overlap.
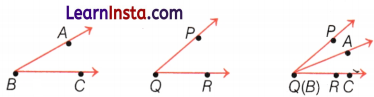
The above figure, shows the two angles are superimposed. It is clear that ∠PQR is larger than ∠ABC.
Equal Angles
If the corners of any two angles match and the arms overlap with each other, then the angles are equal in size.
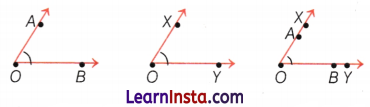
In above figure, there is an equal amount of rotation needed to move \(\overrightarrow{O B}\) to \(\overrightarrow{O A}\) and \(\overrightarrow{O Y}\) to \(\overrightarrow{O X}\). By superimposition, the vertex is common and two rays of both angles lie on top of each other. So, we can say the sizes of angles are equal.
Comparing Angles without Superimposition
Consider two angles, ∠AOB and ∠XOY.
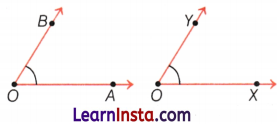
We can compare both these angles without superimposition through a transparent circle.
Let us place the circular paper on the first angle. The circle is placed in such a way that its centre is on the vertex of the angle.
Let us mark the points A and B on the edge circle at the points, where the arms of the angle pass through the circle.
Now, on placing this on other angle (i.e. ∠XOY) we can find that the angle is greater than or equal to or smaller than the first angle.
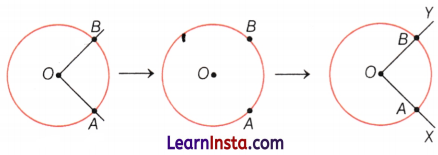
Example 6.
In each case, determine which angle is greater and why?
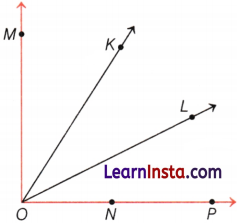
(i) ∠MON or ∠KON
(ii) ∠MON or ∠KOL
(iii) ∠LON or ∠LOP
Solution:
On comparing by superimposition, we get
(i) ∠MON is greater than ∠KON because the amount of rotation of ∠MON is greater than the amount of rotation of ∠KON.
(ii) ∠MON is greater than ∠KOL because size of ∠MON is greater than size of ∠KOL.
(iii) ∠LON and ∠LOP both are equal angle because vertex O and one ray \(\overrightarrow{O L}\) are common and arm \(\overrightarrow{O N}\) and \(\overrightarrow{O P}\) are overlaping.
Example 10.
Compare two angles given below without superimposition and find which angle is smaller?
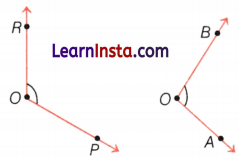
Solution:
Suppose we have a transparent circle which can be moved and placed on figures.
Let us place the circular paper on the ∠POR.
The circle is placed in such a way that its centre is on the vertex of the angle.
Mark the points K and L on the edge circle at the points, where the arms of the angle pass through the circle.
After that put it on other given ∠AOB and check that which is smaller.
Hence, we get ∠AOB is smaller than ∠POR.
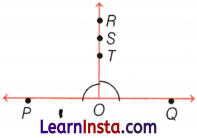
Special Type of Angles
Straight Angle
If the arms forming the angle lie in a straight line, then the angle is called a straight angle.
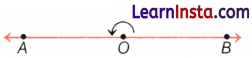
Here, ∠AOB is a straight angle.
![]()
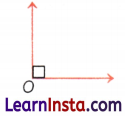
Right Angle
A right angle resembles the shape of letter L. An angle is a right angle only if it is exactly half of a straight angle. Two lines that meet at right angles are called perpendicular lines.
Acute Angles
The angles less than a right angle or less than a quarter turn are called acute angles.

Obtuse Angles
The angles greater than a right angle but less than a straight angle (i.e. turning is more than a quarter turn and less than a half turn) are called obtuse angles.

Example 11.
How many right angles in the figure given below?
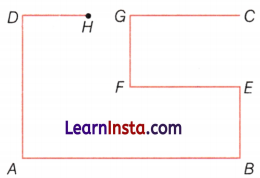
Solution:
On observing the given figure, we find that there are six right angles, which names are as follows.
∠ABE, ∠BAD, ∠ADH, ∠EFG, ∠FGC and ∠BEF.
Example 12.
Find out the number of acute angles in the figure given below.
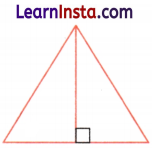
Solution:
Mark the points, A, B, C, and D on the given figure.
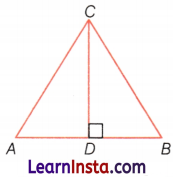
∵ CD is perpendicular to AB, so CD can not make an acute angle with AB.
Acute angles are always less than the right angle.
Here, acute angles are ∠BAC, ∠ACD, ∠DCB, and ∠CBD or ∠CBA.
Hence, there are four acute angles.
Example Problems
Question 1.
Write the name of the angles in the given figure.
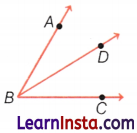
Answer:
∠ABC, ∠ABD, and ∠DBC
Question 2.
Name the vertex and the arms of ∠POQ given below.
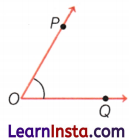
Answer:
Vertex = 0, Arms = OP and QQ
Question 3.
In the following figure, name the angles.
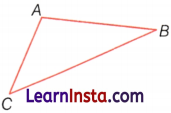
Answer:
∠CAB, ∠ACB, ∠CBA or ∠A, ∠B and ∠C
Question 4.
Name the angle, in the given figure.
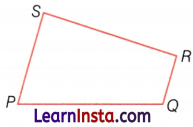
Answer:
(i) ∠S or ∠PSR
(ii) ∠R or ∠SRQ
(iii) ∠P or ∠SPQ
(iv) ∠Q or ∠PQR
Question 5.
Draw rough diagrams of two angles such that they have
(i) one common point.
(ii) three common points.
Answer:
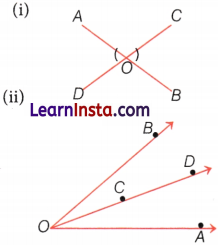
Question 6.
Draw a rough diagram of two angles such that they have one ray in common.
Answer:
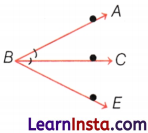
Question 7.
Write the alternate name of the angle ∠DCB, in the given figure.
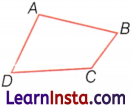
Answer:
∠C
Question 8.
In the following figure, how many angles are there? Name them.
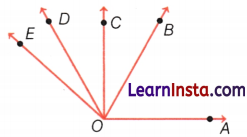
Answer:
There are ten angles.
i.e. ∠EOD, ∠DOC, ∠COB, ∠BOA, ∠EOC, ∠DOB, ∠COA, ∠EOB, ∠DOA and ∠EOA.
![]()
Question 9.
In the figure, name each of the following angles in different ways.
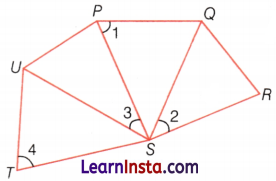
(i) ∠1
(ii) ∠2
(iii) ∠3
(iv) ∠4
Answer:
(i) ∠QPS or ZSPQ
(ii) ∠QSR or ∠RSQ
(iii) ∠PSU or ∠USP
(iv) ∠STU or ∠UTS
Question 10.
Does the vertex of an angle lie in its interior?
Answer:
No
Question 11.
Write the points, that lie interior in the ∠CAD.
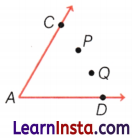
Answer:
Q and P
Question 12.
Name the points, in the given diagram.
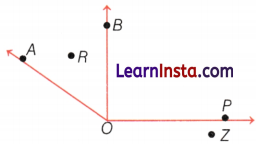
(i) In the interior of ∠AOB.
(ii) In the exterior of ∠BOP.
Answer:
(i) Point R
(ii) A, R and Z
Question 13.
In the figure given below, compare angles by superimposition and determine which angle is greater.
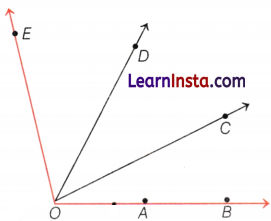
(i) ∠EOD or ∠EOC.
(ii) ∠DOC or ∠AOD.
(iii) ∠COA or ∠BOC.
Answer:
(i) ∠EOC
(ii) ∠AOD
(iii) Both are Equal.
Question 14.
Compare the two angles given below without superimposition and find which angle is smaller.
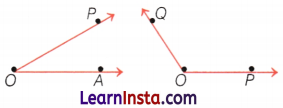
Answer:
∠AOP is smaller.
Question 15.
Join A to other grid points in the figure by a straight line to get a straight angle and a right angle. What are all the different ways of doing it?
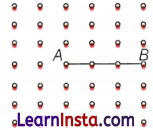
Answer:
Do yourself.
Question 16.
How many right angles are in the figure given below? Write the name of each right angle.
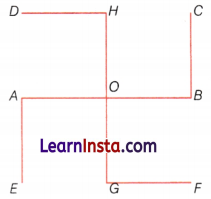
Answer:
There are eight right angles in the given figure.
∠AOG, ∠AOH, ∠BOG, ∠BOH, ∠OBC, ∠OHD, ∠OAE and ∠OGF.
Question 17.
Find out the number of acute angles in the given figure. Name them.
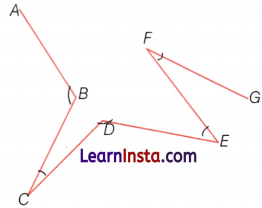
Answer:
The number of acute angles is 3.
∠BCD, ∠DEF, and ∠EFG.
Measuring and Drawing of Angles
Measuring Angles
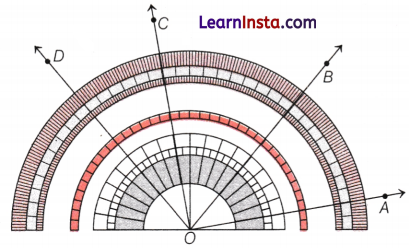
To assign precise measures to angles, mathematicians divided the angle in the centre of the circle into 360 equal angle or parts. The angle measure of each of these unit part is 1 degree, which is written as 1°.

In above picture, it contains 28 units of 1° angle. So, we say that its angle measure is 28°.
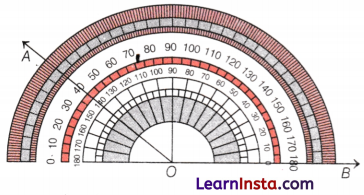
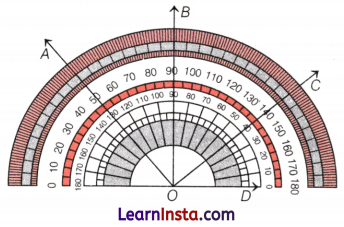
Measuring by Protractor
An unlabelled protractor is shown in the above picture. The straight angle of the center is divided into 180 units of 1 degree. Starting from the marking on the rightmost point of the base, there is a long mark for every 10°, and from every such long mark, there is a medium-sized mark after 5°.
e.g. In the above figure, a measure of ∠AOB is 4 × 10° = 40°.
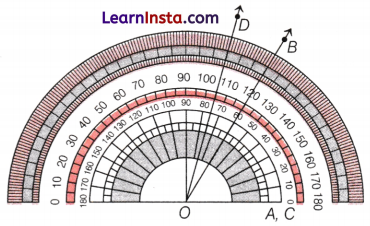
Now, through a labeled protractor, we can find a direct measure of the angles.
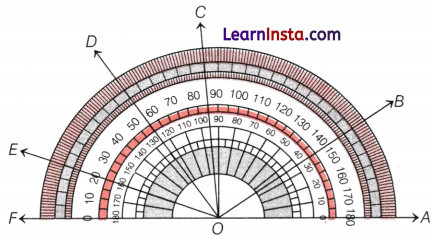
In the above picture of the labeled protractor, there are two sets of numbers on it, one increasing from right to left and the other increasing from left to right.
If we read the number increasing from right to left, then we can find the measure of the angle.
e.g. pleasure of ∠AOB is 35°.
If we read the number increasing from left to right, then we find a correct measure of angle by subtracting the number from 180.
e.g. Measure of ∠AOD = 180° – 55° = 125°.
![]()
Example 1.
Measure the following angle with a protractor.
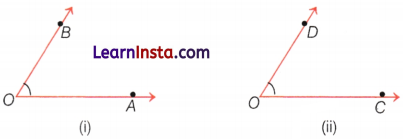
Solution:
On placing the protractor on the given figure of angles, we get
(i) Measure of ∠AOB = 60°
(ii) Measure of ∠COD = 75°
Angle Bisector
In the above figure, \(\overrightarrow{O C}\) splits the ∠AOB into two equal angles.
The process of getting half of a given angle is called bisecting the angle.
The line bisects a given angle is called the angle bisector of the angle.
Example 2.
In the given figure, it measure of ∠AOB is 75° and \(\overrightarrow{O C}\) is the angle bisector of ∠AOB, then find the measure of ∠COB.
Solution:
Given that ∠AOB = 75° and \(\overrightarrow{O C}\) is the angle bisector of ∠AOB.
∵ Angle bisector \(\overrightarrow{O C}\) bisects the given ∠AOB into two equal parts.
So, ∠AOC = ∠COB
Also, ∠AOC + ∠COB = ∠AOB = 75°
∠COB = \(\frac{75}{2}\) = 37½°
Hence, the measure of ∠COB is 37½°.
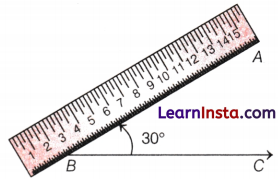
Drawing Angles
Suppose we have to draw a 30° angle using a protractor. For this, let us name it ∠ABC.
Now, in ∠ABC, B will be the vertex, and BA and BC will be the arms of the angle.
For drawing angle, firstly we take one arm (i.e. BC), as the reference (base) and another arm BA with a turn of 30°.
For drawing ∠ABC = 30°, we will follow the steps as following:
Step I: We begin with the base and draw \(\overrightarrow{B C}\).
![]()
Step II: Place the center point of the protractor on B and align BC to the O line.
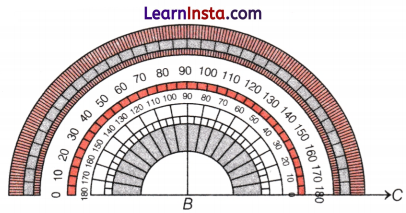
Step III Now, starting from 0 count your degrees (0, 10, 20, 30) upto 30 on the protractor. Mark point A at the label 30°.
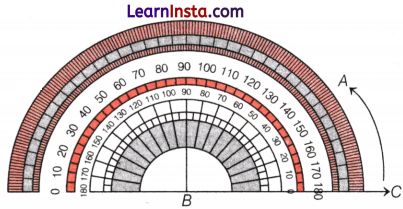
Step IV: Using a ruler, join the points B and A.
∠ABC = 30° is the required angle.
Types of Angles and their Measures
We have seen that a straight angle is 180° and a right angle is 90°. Other types of angles i.e. acute and obtuse angles in terms of their degree measure are as follows.
Acute Angle
Angles that are smaller than the right angle (i.e. less than 90°) and greater than 0° are called acute angles.
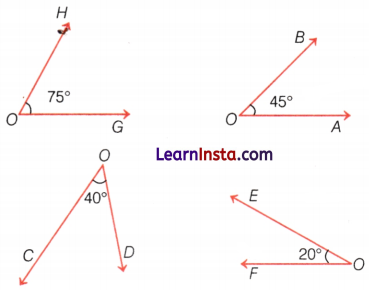
Obtuse Angle
Angles, which are greater than 90° and less than 180° (i.e. greater than right angle and less than straight angle) are called obtuse angles.

Reflex Angle:
Angles, which are greater than 180° and less than 360° (i.e. greater than a straight angle and less than the whole angle) are called reflex angles.
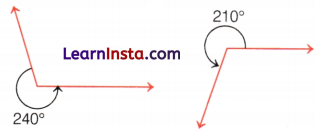
Example 3.
Using a protractor, find the measure of the angle given below, also classify the type of angle.
Solution:
Using a protractor, we get ∠AOB = 140°
∵ 180° > 140° > 90°
So, ∠AOB is an obtuse angle.
Example 4.
In the figure given below, use a protractor to find the measure of each angle. Then, classify each angle as acute, obtuse, right, or reflex.
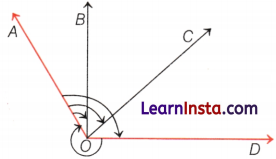
(i) ∠AOB
(ii) ∠AOC
(iii) ∠AOD
(iv) ∠DOA
Solution:
On measuring by a protractor as
(i) ∠AOB = ∠DOA – ∠DOB = 130 ° – 90 ° = 40 °, which is an acute angle.
(ii) ∠AOC = ∠AOD – ∠COD = 130° – 40° = 90 °, which is a right angle.
(iii) ∠AOD = 130°, which is an obtuse angle.
(iv) ∠DOA = 360° – ∠AOD = 360° – 130° = 230°, which is reflex angle.
[∵ whole angle = 360°]
Example Problems
Question 1.
Measure the following angle (figure given below) using a protractor.
Answer:
(i) 35°
(ii) 45°
(iii) 120°
Question 2.
In the given figure, if the measure of ∠AOB is 110° and \(\overrightarrow{O C}\) is the angle bisector of ∠AOB then without using a protractor, find the measure of ∠COB.
Answer:
∠COB = 55°
![]()
Question 3.
Using a protractor, draw the following angles.
(i) 40°
(ii) 60°
(iii) 75°
(iv) 105°
Answer:
Do yourself.
Question 4.
Classify the angles given below as acute, obtuse, right, or reflex.
(i) 45°
(ii) 35°
(iii) 90°
(iv) 108°
(v) 215°
Answer:
(I) Acute Angle
(Ii) Acute Angle
(Iii) Right Angle
(Iv) Obtuse Angle
(V) Reflex Angle
Question 5.
Using a protractor, find the measure of the angle given below, also classify the type of angle.
Answer:
∠AOB = 150°, Obtuse Angle.
→ Points, lines, and planes are the basic elements that form the foundation of geometry. The word ‘Geometry’ is drawn from the Greek word ‘Geometron’ where ‘Geo’ means Earth and ‘metron’ means measurement. By the sharp tip of your pencil mark a dot on the paper.
→ This dot gives an idea of a point. A point determines a location. The shortest distance between two points is called a line segment.
→ If a line segment extends beyond the endpoints indefinitely in both directions then we get a model of a line. A flat surface gives an idea of a plane.
→ The basic idea of a plane is that it is a flat surface that extends indefinitely in all directions. Two rays starting from a common endpoint make an angle. The common endpoint is called the vertex of the angle.
![]()
→ Points, lines, and planes are the basic elements in geometry.
→ Point does not have length, breadth, or thickness. It determines a location.
→ The basic idea of a line is that it is straight and extends indefinitely in both directions.
→ A part of a line is called a line segment. It is the shortest distance between two points.
→ A line segment has two endpoints.
→ A ray is a portion of the line starting at one point (called the starting or initial point of the ray) and extending in one direction endlessly.
→ If two distinct lines meet at a point, they are called intersecting lines.
→ Two parallel lines in a plane do not meet each other.
→ An angle is made up of two rays starting from a common endpoint. The common point is called its vertex and the two rays are called the arms of the angle.
→ An angle is measured in degrees.
![]()
→ Angles are measured using an instrument called a protractor.
→ The measure of a right angle is 90°.
→ The measure of a straight angle is 180°.
→ An acute angle has its measure smaller than that of a right angle whereas an obtuse angle has its measure greater than a right angle but less than a straight angle.
→ An angle having its measure greater than a straight angle is called a reflex angle.
→ Two intersecting lines are perpendicular if the angle between them is 90°.