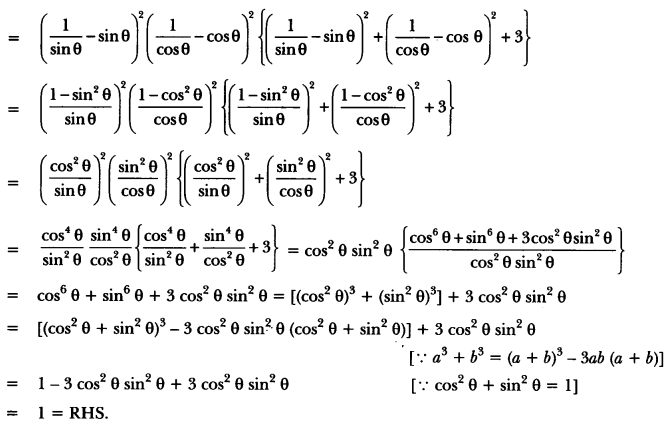Introduction to Trigonometry Class 10 Extra Questions Maths Chapter 8 with Solutions Answers

Here we are providing Introduction to Trigonometry Class 10 Extra Questions Maths Chapter 8 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.

Extra Questions for Class 10 Maths Introduction to Trigonometry with Answers Solutions

Extra Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry with Solutions Answers

Introduction to Trigonometry Class 10 Extra Questions Short Answer Type 1

Question 1.
Find maximum value of \(\frac{1}{\sec \theta}\), 0°≤ θ ≤ 90°.
Solution:
\(\frac{1}{\sec \theta}\), (0° ≤ θ ≤ 90°) (Given)
∵ sec θ is in the denominator
∴ The min. value of sec θ will return max. value for \(\frac{1}{\sec \theta}\).
But the min. value of sec θ is sec 0° = 1.
Hence, the max. value of \(\frac{1}{\sec 0^{\circ}}\) = \(\frac{1}{1}\) = 1

Question 2.
Given that sin θ = \(\frac{a}{b}\), find the value of tan θ.
Solution:
sin θ = \(\frac{a}{b}\)

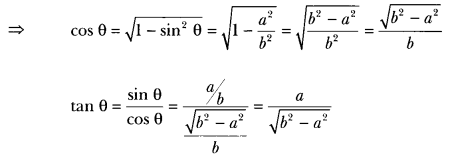
Question 3.
If sin θ = cos θ, then find the value of 2 tan θ + cos² θ.
Solution:
sin θ = cos θ (Given)
It means value of θ = 45°
Now, 2 tan θ + cos² θ = 2 tan 45° + cos² 45°

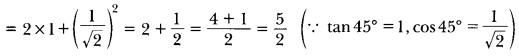
Question 4.
If sin (x – 20)° = cos (3x – 10)°, then find the value of x.
Solution:
sin (x – 20)° = cos (3x – 10)°
⇒ cos [90° – (x – 20)°] = cos (3x – 10)°
By comparing the coefficient
90° – x° + 20° = 3x° – 10° = 110° + 10° = 3x° + x°
120° = 4x°
⇒ \(\frac{120^{\circ}}{4}\) = 30°

Question 5.
If sin² A = \(\frac{1}{2}\)tan² 45°, where A is an acute angle, then find the value of A.
Solution:
sin²A = \(\frac{1}{2}\)tan² 45°
⇒ sin²A = \(\frac{1}{2}\) (1)² [∵ tan 45° = 1]
= sin² A = \(\frac{1}{2}\)
⇒ sin A = \(\frac{1}{\sqrt{2}}\)
Hence, ∠A = 45°

Question 6.
If x = a cos θ, y = b sin θ, then find the value of b²x² + a²y² – a²b².
Solution:
Given x = acos θ, y = b sin θ
b²x² + a²y² – a²b² = b²(acos θ)² + a²(b sin θ)² – a²b²
= a²b² cos²θ + a²b² sin² θ – a²b² = a²b² (sin² θ + cos² θ) – a²b²
= a²b² – a²b² = θ (∵ sin² θ + cos² θ = 1)

Question 7.
If tan A = cot B, prove that A + B = 90°.
Solution: We have
tan A = cot B
⇒ tan A = tan (90° – B)
A = 90° – B
[∵ Both A and B are acute angles]
⇒ A + B = 90°

Question 8.
If sec A = 2x and tan A = \(\frac{2}{x}\), find the value of 2\(\left(x^{2}-\frac{1}{x^{2}}\right)\) .
Solution:

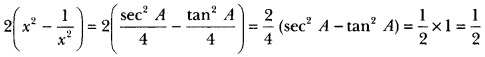
Question 9.
In a ∆ABC, if ∠C = 90°, prove that sin² A + sin² B = 1.
Solution:
Since ∠C = 90°
∴ ∠A + ∠B = 180° – ∠C = 90°
Now, sin² A + sin² B = sin² A + sin² (90° – A) = sin² A + cos² A = 1

Question 10.
If sec 4A = cosec (A – 20°) where 4 A is an acute angle, find the value of A.
Solution:
We have
sec 4 A = cosec (A – 20°)
⇒ cosec (90° – 4 A) = cosec (A – 20°)
∴ 90° – 4 A = A – 20°
⇒ 90° + 20° = A + 4 A
⇒ 110° = 5 A
∴ A = \(\frac{110}{5}\) = 22°

Introduction to Trigonometry Class 10 Extra Questions Short Answer Type 2

Question 1.
If sin A = \(\frac{3}{4}\), calculate cos A and tan A.
Solution:
Let us first draw a right ∆ABC in which ∠C = 90°.
Now, we know that

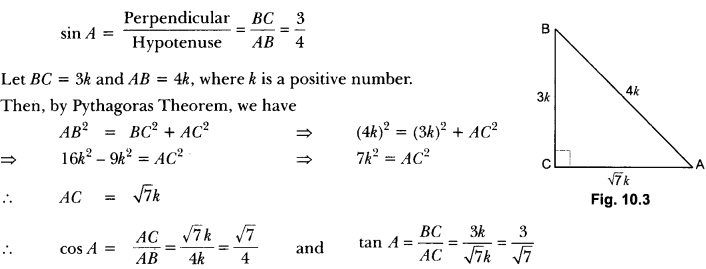
Question 2.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Let us first draw a right ∆ABC in which ∠B = 90°.
Now, we have, 15 cot A = 8

Question 3.
In Fig. 10.5, find tan P – cot R.
Solution:

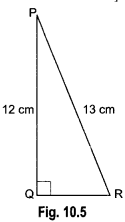
Using Pythagoras Theorem, we have
PR² = PO² + QR²
⇒ (13)² = (12)² + QR²
⇒ 169 = 144 + QR²
⇒ QR² = 169 – 144 = 25
⇒ QR = 5 cm
Now, tan P = \(\frac{QR}{PQ}\) = \(\frac{5}{12}\) and cot R = \(\frac{QR}{PQ}\) = \(\frac{5}{12}\)
tan P – cot R = \(\frac{5}{12}\) – \(\frac{5}{12}\) = 0

Question 4.
If sin θ + cos θ = √3 , then prove that tan θ + cot θ = 1.
Solution:
sin θ + cos θ = √3
⇒ (sin θ + cos θ)² = 3
⇒ sin² θ + cos² θ + 2 sin θ cos θ = 3
⇒ 2 sin cos θ = 2 (∵ sin² θ + cos² θ = 1)
⇒ sin θ. cos θ = 1 = sin² θ + cos² θ

⇒ 1 = tan θ + cot θ = 1
Therefore tan θ + cot θ = 1

Question 5.
Prove that \(\frac { 1-sinθ }{ 1+sinθ } \) = (sec θ – tan θ)²
Solution:

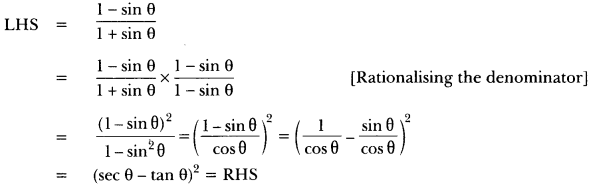
Without using tables, evaluate the following (6 to 10).

Question 6.

Solution:

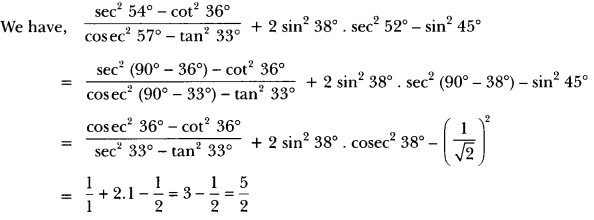
Question 7.

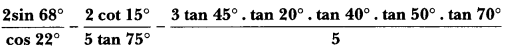
Solution:

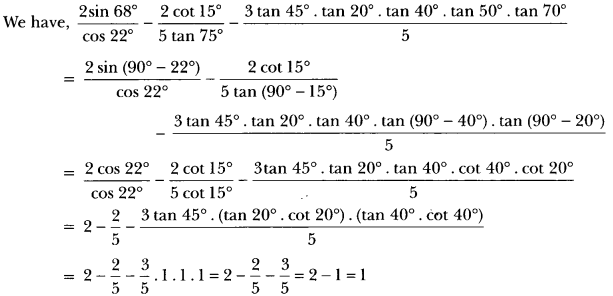
Question 8.

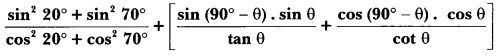
Solution:

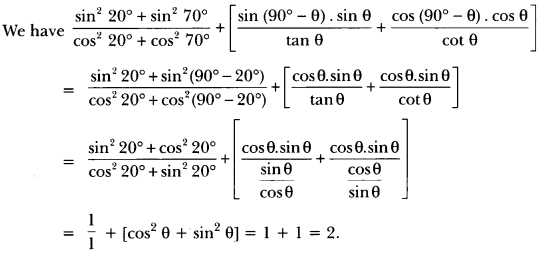
Question 9.
Evaluate: sin 25° cos 65° + cos 25° sin 65°.
Solution:
sin 25°. cos 65° + cos 25° . sin 65°
= sin (90° – 65°). cos 65° + cos (90° – 65°). sin 65°
= cos 65° . cos 65° + sin 65°. sin 65°
= cos² 65° + sin² 65° = 1.

Question 10.
Without using tables, evaluate the following:
3 cos 68°. cosec 22° – \(\frac{1}{2}\) tan 43°. tan 47°. tan 12°. tan 60°. tan 78°
Solution:
We have,
3 cos 68°. cosec 22° – \(\frac{1}{2}\) tan 43°. tan 47°. tan 12°. tan 60°. tan 78°.
= 3 cos (90° – 22°). cosec 22° – \(\frac{1}{2}\) . {tan 43° . tan (90° – 43°)}. {tan 12°. tan (90° – 12°). tan 60°}
= 3 sin 22°. cosec 22° – \(\frac{1}{2}\)(tan 43° . cot 43°). (tan 12°. cot 12°). tan 60°
= 3 × 1 – × 1 × 1 × √3 = 3 – \(\frac{\sqrt{3}}{2}\) = \(\frac{6-\sqrt{3}}{2}\).

Question 11.
If sin 30 = cos (θ – 6°) where 30 and (θ – 6°) are both acute angles, find the value of θ.
Solution:
According to question:
sin 3θ = cos (θ – 6°)
cos (90° – 30) = cos (θ – 6°) [∵ cos (90° – θ ) = sin θ]
90° – 3θ = θ – 6° [comparing the angles)
= 4θ = 90° + 6° = 96°
θ = \(\frac{96}{4}\) = 24°
Hence, θ = 24°

Question 12.
If sec θ = x + \(\frac{1}{4x}\), prove that sec θ + tan θ = 2x or \(\frac{1}{2x}\).
Solution:
Let sec θ + tan θ = λ …..(i)
We know that, sec² θ – tan² θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
⇒ λ(sec θ – tan θ) = 1
sec θ – tan θ = \(\frac{1}{\lambda}\) …..(ii)
Adding equations (i) and (ii), we get

Question 13.
Find an acute angle θ, when

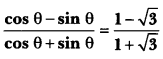
Solution:

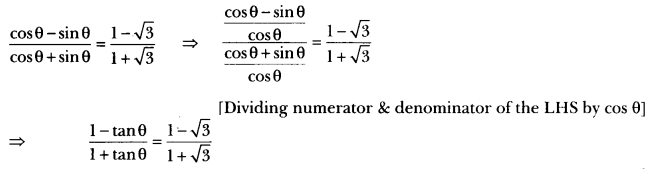
On comparing we get
⇒ tan θ = √3
⇒ tan θ = tan 60°
= θ = 60°

Question 14.
The altitude AD of a MABC, in which ∠A is an obtuse angle has length 10 cm. If BD = 10 cm and CD = 10√3 cm, determine ∠A.
Solution:

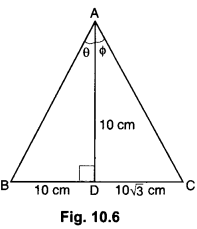
∆ABD is a right triangle right angled at D, such that AD = 10 cm and BD = 10 cm.
Let ∠BAD = θ
∴ tan θ = \(\frac{B D}{A D}\)
⇒ tan θ = \(\frac{10}{10}\) = 1
⇒ tan θ = tan 45°
⇒ θ = ∠BAD = 45° … (i)
∆ACD is a right triangle right angled at D such that AD = 10 cm and DC = 10√3 cm.
Let ∠CAD = Φ
∴ tan Φ = \(\frac{CD}{AD}\)
⇒ tan Φ = \(\frac{10 \sqrt{3}}{10}\) = √3
⇒ tan Φ = tan 60°
⇒ Φ = ∠CAD = 60°
From (i) & (ii), we have
∠BAC = ∠BAD + ∠CAD = 45° + 60° = 105°

Question 15.
If cosec θ = \(\frac{13}{12}\), evaluate \(\frac{2 \sin \theta-3 \cos \theta}{4 \sin \theta-9 \cos \theta}\)
Solution:

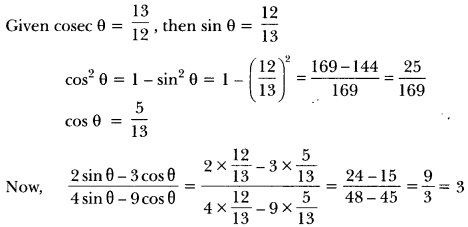
Question 16.
Prove that

Solution:

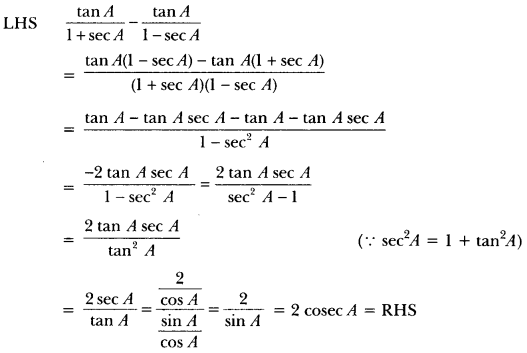
Question 17.
Prove that

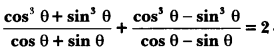
Solution:
We have,

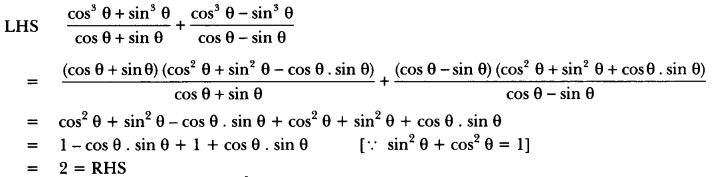
Question 18.
Prove that:

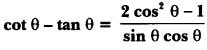
Solution:

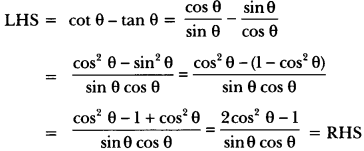
Question 19.
Prove that:

Solution:

Question 20.
Evaluate the following:

Solution:

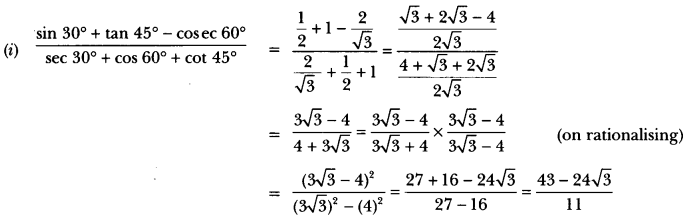
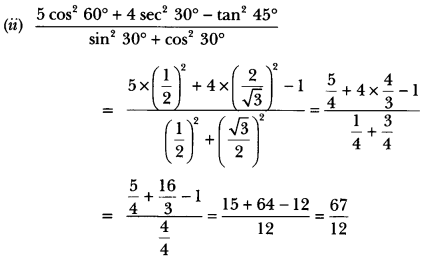
Question 21.
If tan (A +B) = √3 and tan (A – B) = \(\frac{1}{\sqrt{3}}\); 0° < A + B ≤ 90°; A > B, find A and B.
Solution:
We have, tan (A + B) = √3
⇒ tan (A + B) = tan 60°
∴ A + B = 60° …(i)
Again, tan (A – B) = \(\frac{1}{\sqrt{3}}\)
∴ A – B = 30° … (ii)
Adding (i) and (ii), we have
2A = 90°
⇒ A = 45°
Putting the value of A in (i), we have
45° + B = 60°
∴ B = 60° – 45o = 15°
Hence, A = 45° and B = 15°

Question 22.
If A, B and C are interior angles of a ∆ABC, then show that sin \(\left(\frac{B+C}{2}\right)\) = cos\(\frac{A}{2}\).
Solution:
Since A, B and C are the interior angles of a ∆ABC,

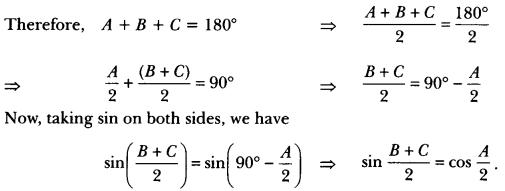
Question 23.
Prove that: (cosec θ – cot θ)² = \(\frac {1-\cos\theta}{1+\cos\theta}\)
Solution:
LHS = (cosec θ – cot θ)²

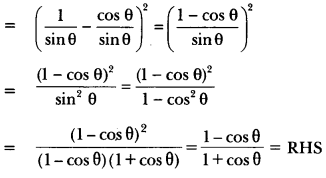
Question 24.
Prove that:

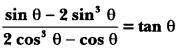
Solution:

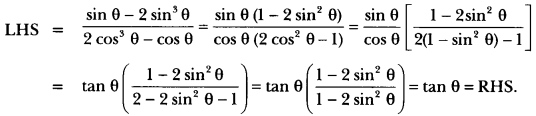
Question 25.
Prove that: (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot²A.
Solution:
LHS = (sin A + cosec A)² + (cos A + sec A)²
= sin² A + coses² A + 2sin A . cosec A + cos² A + sec² A + 2 cos A . sec A
= (sin² A + coses² A + 2) + (cos² A + sec² A + 2) [sin A. cosec A = 1]
= (sin² A + cos² A) + (coses² A + sec² A) + 4 [cos A. sec A = 1]
= 1 + 1 + cot²A + 1 + tan² A + 4
= 7 + tan² A + cot² A = RHS [∵ 1 + cot²A = coses² A and 1 + tan² A = sec² A]

Question 26.
Prove that:

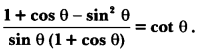
Solution:

To obtain cot θ in RHS, we have to convert the numerator of LHS in cosine function and denominator in sine function.
Therefore converting sin² θ = 1 – cos² θ, we get

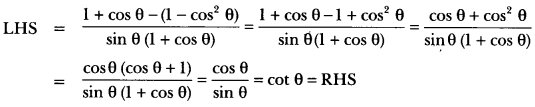
Question 27.
Prove that:

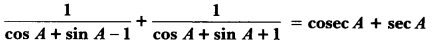
Solution:

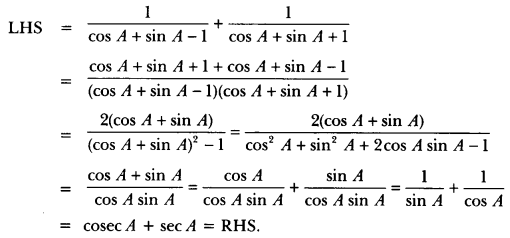
Question 28.
Prove that:

Solution:

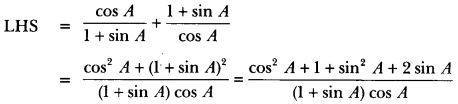
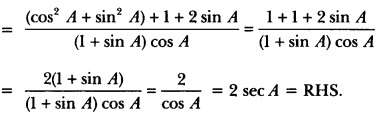
Question 29.
Without using trigonometric tables, prove that:

Solution:

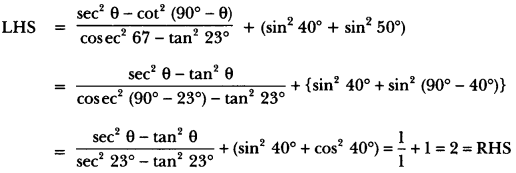
Question 30.
Evaluate:

Solution:

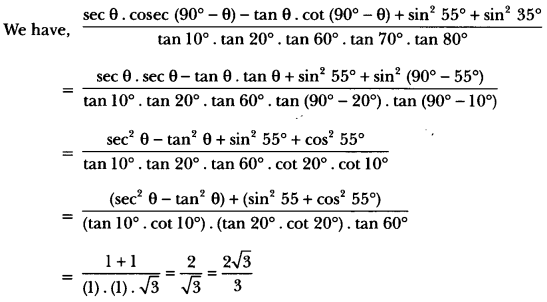
Introduction to Trigonometry Class 10 Extra Questions Long Answer Type

Question 1.
In ∆PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

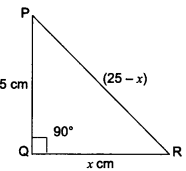
We have a right-angled ∆PQR in which ∠Q = 90°.
Let QR = x cm
Therefore, PR = (25 – x) cm
By Pythagoras Theorem, we have
PR² = PQ² + QR²
(25 – x)² = 5² + x²
= (25 – x)² – x² = 25
(25 – x – x) (25 – x + x) = 25
(25 – 2x) 25 = 25
25 – 2x = 1
25 – 1 = 2x
= 24 = 2x
∴ x = 12 cm
Hence, QR = 12 cm
PR = (25 – x) cm = 25 – 12 = 13 cm
PQ = 5 cm

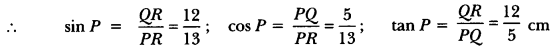
Question 2.
In triangle ABC right-angled at B, if tan A = \(\frac{1}{\sqrt{3}}\) find the value of:
(i) sin A cos C + cos A sin C (ii) cos A cos C – sin A sin C.
Solution:

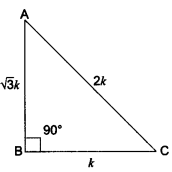
We have a right-angled ∆ABC in which ∠B = 90°.
and, tan A = \(\frac{1}{\sqrt{3}}\)
Now, tan A = \(\frac{1}{\sqrt{3}}\) = \(\frac{BC}{AB}\)
Let BC = k and AB = √3k
∴ By Pythagoras Theorem, we have
⇒ AC² = AB² + BC²
⇒ AC² = (√3k)² + (k)² = 3k² + k²
⇒ AC² = 4k²

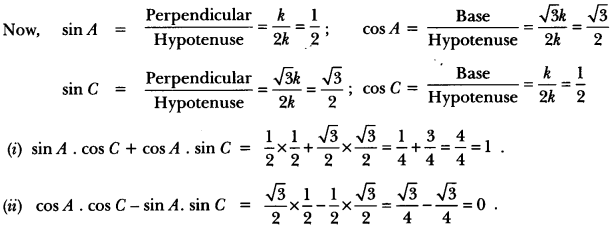
Question 3.
If cot θ = \(\frac{7}{8}\), evaluate:
(i)

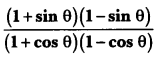
(ii) cot² θ
Solution:
Let us draw a right triangle ABC in which ∠B = 90° and ∠C = θ.

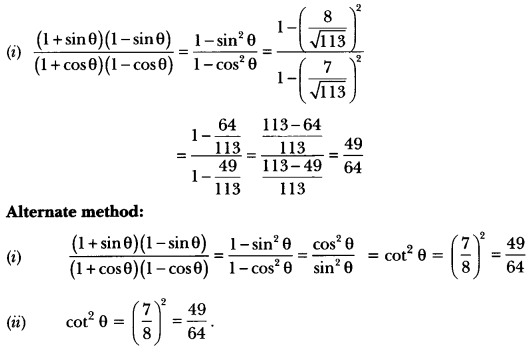
Question 4.
If 3 cot A = 4, check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not.
Solution:

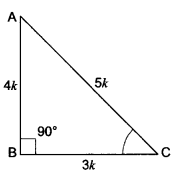
Let us consider a right triangle ABC in which ∠B = 90°

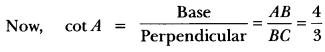
Let AB = 4k and BC = 3k
∴ By Pythagoras Theorem
AC² = AB² + BC²
AC = (4k)² + (3k)² = 16k² + 9k²
AC² = 25k²
∴ AC = 5k

Question 5.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:

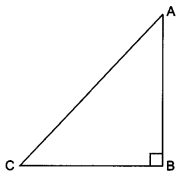
Let us consider a right-angled ∆ABC in which ∠B = 90°.
For ∠A we have

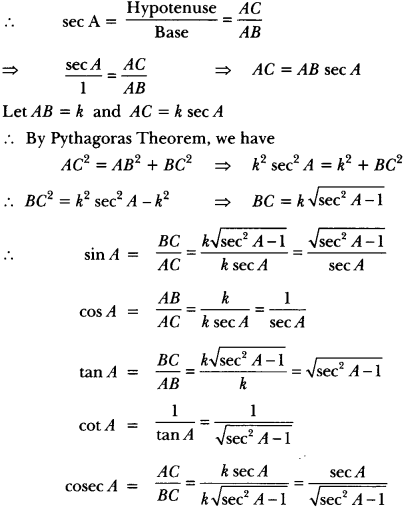
Question 6.
Prove that

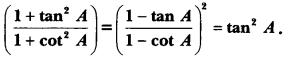
Solution:

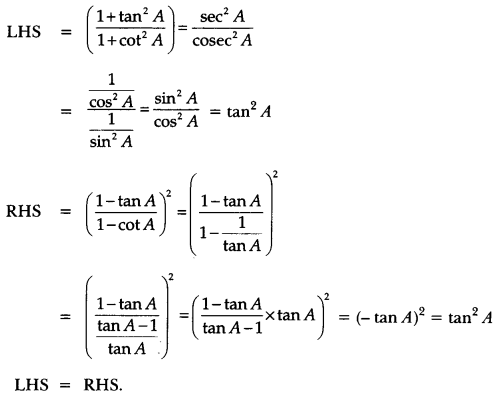
Question 7.
Prove that:

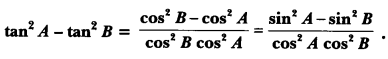
Solution:

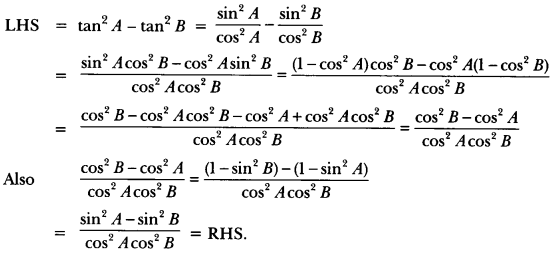
Question 8.
Prove that

Solution:

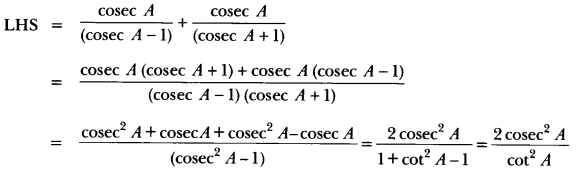
= 2 cosec² A tan² A = 2(1 + cot² A). tan² A
= 2 tan² A + 2 tan² A. cot² A (∵ tan A cot A = 1)
= 2 + 2 tan² A = 2(1 + tan² A) = 2 sec² A = RHS.

Question 9.
Prove that: (sin θ + sec θ)² + (cos θ + cosec θ)² = (1 + sec θ cosec θ)².
Solution:
LHS = (sin θ + sec θ)2 + (cos θ + cosec θ)²

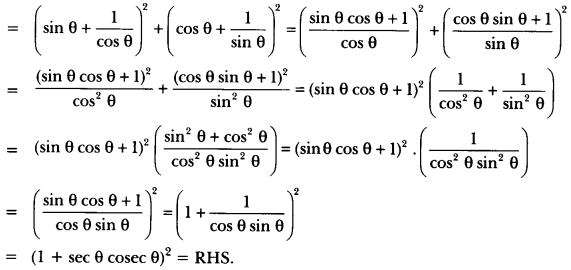
= (1 + sec θ cosec θ)² = RHS.

Question 10.
Prove that:

Solution:
In order to show that,

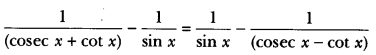
Question 11.
Prove that: \(\frac { cosecθ\quad +\quad cotθ }{ cosecθ\quad -\quad cotθ } \) = (cosec θ + cot θ) = 1 + 2 cot² θ + 2 cosec θ cot θ.
Solution:

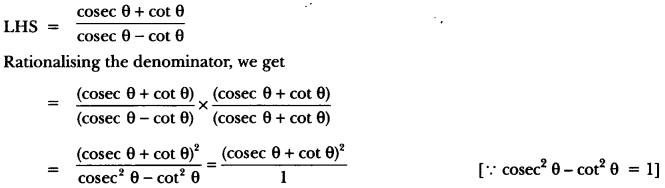
= cosec² θ + cot² θ + 2 cosec θ. cot θ
= (1 + cot² θ) + cot² θ + 2 cosec θ. cot θ
= 1 + 2 cot² θ + 2 cosec . cot θ = RHS.

Question 12.
Prove that: 2 sec θ – sec θ – 2 cosec θ + cosec θ = cot – tan θ.
Solution:
LHS = 2 sec θ – sec θ – 2 cosec² θ + cosec θ
= 2 (sec² θ) – (sec² θ)2 – 2 (cosec² θ) + (cosec θ)²
= 2 (1 + tan² θ) – (1 + tan⁴ θ)2 – 2(1 + cot² θ) + (1 + cot² θ)⁴
= 2 + 2 tan² θ – (1 + 2 tan² θ + tan² θ) – 2 – 2 cot² θ + (1 + 2 cot² θ + cot θ) =
= 2 + 2 tan² θ – 1 – 2 tan² θ – tan⁴ θ – 2 – 2 cot² θ + 1 + 2 cot⁴ θ + cot⁴ θ
= cot⁴ θ – tan⁴ θ = RHS

Question 13.
Prove that: (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\).
Solution:
LHS = (cosec A – sin A) (sec A – cos A)

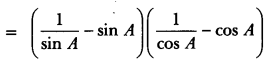
Introduction to Trigonometry Class 10 Extra Questions HOTS

Question 1.
Prove that:
\(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ = 1 + tan θ + cot θ.
Solution:

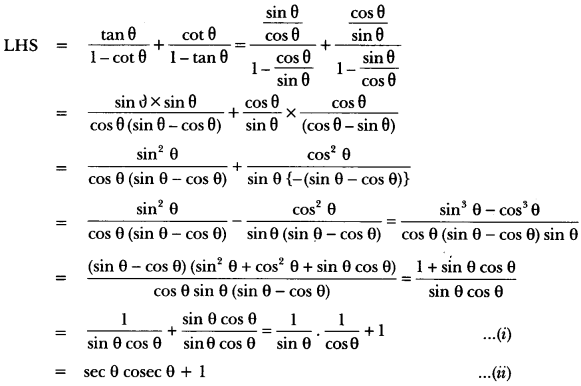
For second part
Now from (i), we have

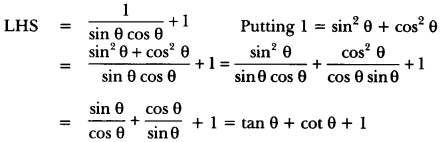
Question 2.
If tan A = n tan B and sin A = m sin B, prove that cos² A = \(\frac{m^{2}-1}{n^{2}-1}\)
Solution:
We have to find cos² A in terms of m and n. This means that the angle B is to be eliminated from
the given relations.
Now, tan A = n tan B
⇒ tan B = \(\frac{1}{n}\) tan A
⇒ cot B = \(\frac{n}{\tan A}\)
and
sin A = m sin B

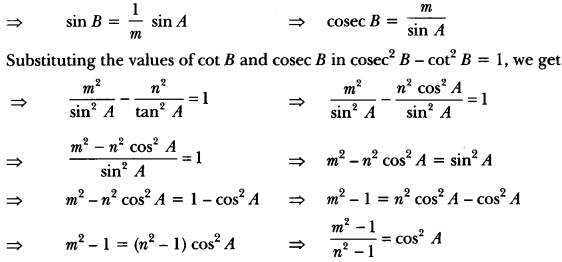
Question 3.
Prove the following identity, where the angle involved is acute angle for which the expressions are defined.
\(\frac { cosA-sinA+1 }{ cos A + sin A-1 } \) = cosec A + cot A, using the identity cosec² A = 1 + cot² A.
Solution:

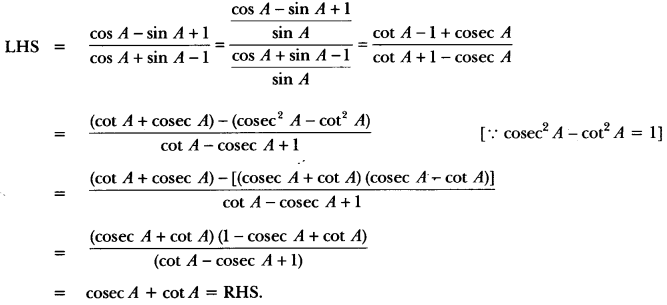
= cosec A + cot A = RHS.

Question 4.
If x sin³ + y cos³ θ = sin θ cos θ and x sin θ = y cos θ, prove x² + y² = 1.
Solution:
We have, x sin³ + y cos³ θ = sin θ cos θ
⇒(x sin θ) sin² θ + (y cos θ) cos² θ sin θ cos θ
⇒ x sin θ (sin² θ) + (x sin θ) cos² = sin θ cos [∵ x sin θ = y cos θ]
⇒ x sin θ (sin² θ + cos² θ) = sin θ cos θ
⇒ x sin θ = sin θ cos
⇒ x = cos θ
Now, we have x sin θ = y cos θ
⇒ cos o sin θ = y cos θ [∵ x = cos θ]
⇒ y = sin θ
Hence, x² + y² = cos² θ + sin² θ = 1.

Question 5.
If tan θ + sin θ = m and tan θ – sin θ = n, show that (m² – n²) = 4√mn.
Solution:
We have, given tan θ + sin θ = m, and tan θ – sin θ = n, then
LHS = (m² – n²),= (tan θ + sin θ)² – (tan θ – sin )²
= tan² θ + sin² θ + 2 tan θ sin θ – tan² θ – sin² θ + 2 tan θ sin θ

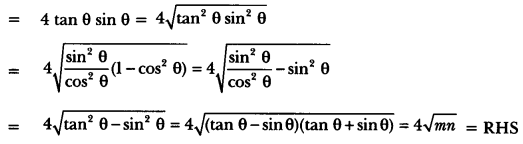
Question 6.
If cosec θ – sin θ = l and sec θ – cos θ = m, prove that l² m² (l² + m² + 3) = 1.
Solution:
LHS = l² m² (l² + m² + 3).
= (cosec θ – sin θ)² (sec θ – cos θ)² {(cosec θ – sin θ)² + (sec θ – cos θ)² + 3}