
On this page, you will find Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 3 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 3 Introduction to Euclid’s Geometry will seemingly help them to revise the important concepts in less time.
CBSE Class 9 Maths Chapter 3 Notes Introduction to Euclid’s Geometry
Introduction to Euclid’s Geometry Class 9 Notes Understanding the Lesson
1. The word ‘geometry is derived from the Greek Word ‘Geo’ means Earth and ‘matrein’ means to measure,
2. In India the excavations of Harappa and Mohenjo-daro show the industrially civilisation (about 300 BCE) made use of geometry.
3. Sulbasutras were the manuals of geometrical constructions in (800 BCE to 500 BCE)
4. The Sriyantra (given in Atharvaveda) which consist 9 interwoven isosceles triangles. These triangles are arranged in such a way that they produce 43 subsidiary triangles.
5. Thales was a great mathematician who gives the proof and statement that a circle is bisected by its diameter.
6. Thales famous pupil was Pythagoaras (572 BCE). He and his group developed the theory of geometry to a great extent.
7. Euclid was a teacher of mathematics at Alexandria in Egypt collect all the famous work and arranged it in his famous treatise called ‘Elements’. He divided the elements in thirteen chapters which are each called a book. These books influenced the whole worlds to understand geometry.
Definitions which are given by Euclid
- Point-, a point is that which has no part.
- Line: A line is breadthless length.
- The ends of a line are points.
- Straight line: It is a line which lies evenly with the points on itself.
- Surface: A surface is that which has length and breadth only.
- Edge: The edges of a surface are lines.
- Plane surface: A plane surface is a surface which lies evenly with the straight lines on itself
If we study these definitions, we find the some of terms like part, length, breadth, evenly, etc. need to be further described clearly. Euclid assumed certain properties, which were not to be proved. Euclid’s assumptions are universal truths,
- Axiom: The basic facts which are taken for granted without proofs are called axiom.
- Statement: A sentence which is either true or false but both is called a statement.
- Theorem: A statement which requires proof.
Euclid’s Axioms
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- If equals are subtracted from equals the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
- Things which are double of the same things are equal to one another.
- Things which are halves of the same things are equal to one another.
Collinear points: Three or more points are said to be collinear, if they all lie in the same line.
Plane: A plane is a flat, two dimensional surface that extends infinitely in all directions. Intersecting lines: Two lines land m are said to be intersecting lines if l and m have only one point common.
Playfair Axiom: Two intersecting lines cannot both be parallel to a same line.
Plane figure: A figure that exist in a plane is called a plane figure.
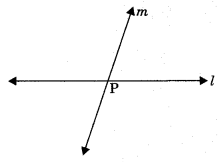
Note:
- Common notions often called axioms.
- Postulates were the assumptions that are specific for geometry.
Axiom 5.1: There is a unique line that passes through two distinct points.
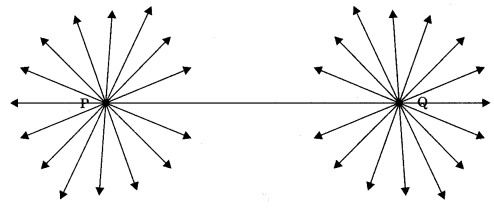
1. Through a given point infinitely many lines can be drawn.
2. A line contains infinitely many points.
Euclid’s five postulates
Postulate 1: A straight line may be drawn from any one point to any other point.
Note: This postulate tells us that one and only one (unique) line passes through two distinct points.
Postulate 2: A terminated line can be produced indefinitely.
This postulate tells us that a line segment can be extended on either side to form a line.
Postulate 3: A circle can be drawn with any centre and any radius.
Postulates 4: All right angles are equal to one another.
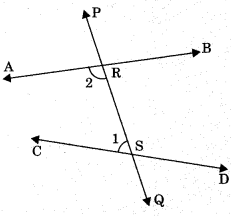
Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
Example: Sum of ∠1 and ∠2 is less than 180°. Therefore, the lines AB and CD will enventually intersect on the left side of PQ. Nowadays, axioms and postulates are used in same sense.
Note: The statements that were proved are called propositions or theorems.
I Euclid deduced 465 propositions in a logical chain by using his axioms,
Theorem 5.1
Two distinct lines can not have more than one point in common,
Proof: Let us suppose that two lines l and m intersect in two distinct points say P and Q. Therefore two lines passing through two distinct points P and Q. But our assumption clashes with the axiom that only one line can pass through two distinct points. So, the assumption was wrong that we started with, that two lines can pass through two distinct points is wrong. Hence two distinct lines can passe through one common point.