Coordinate Geometry Class 9 Notes Advanced Maths Chapter 4

Experts have designed these NCERT Class 9 Advanced Maths Solutions and Class 9 Advanced Maths Chapter 4 Coordinate Geometry Notes for effective learning.

Coordinate Geometry Notes Class 9 Advanced Maths

Introduction

Coordinate geometry uses numbers and coordinates to represent points on a plane. By combining the ideas of algebra and geometry, it helps us study shapes, lines, distances and positions in a precise and visual way. Using the coordinate plane, we can describe locations, draw graphs and solve geometric problems using algebraic methods. It forms the foundation for many real-life applications such as navigation, engineering, computer graphics, architecture and astronomy.
Cartesian System and Slopes of Lines

Language of Graphs

To locate a star in the sky or a seat in a large stadium accurately, we need a proper reference system. In math-ematics, this system is called Coordinate Geometry.
Coordinate geometry uses numbers and coordinates to show the exact position of points on a plane.
It combines algebra and geometry to help us study shapes, lines, distances and positions systematically.

The Cartesian System
Invented by Rene Descartes, this system uses two per-pendicular lines, called axes, labelled the x-axis (horizon-tal) and the y-axis (vertical).

It allows any point in the plane to be described by an or-dered pair of numbers (x, y), known as coordinates.
The axes divide the plane into four quadrants.

Fundamentals;
Cartesian: This term is derived directly from the Latin form of Rene Descartes’ name, Renatus Cartesius.

Coordinates: An ordered pair (x, y) represents the position of a point P, where x shows the horizontal distance (abscissa) and y shows the vertical distance (ordinate).

For example: The points A(3, 4), B(5, -2) and C(-4, 1) as shown in the graph below, represent points in a coordinate plane.

Quadrants
The x and y-axes divide the Cartesian plane into four regions, known as quadrants. These quadrants are numbered in an anticlockwise direction.

1. Quadrant I: Where both x and y are positive.
2. Quadrant II: Where x is negative, but y is positive.
3. Quadrant III: Where both x and y are negative.
4. Quadrant IV: Where x is positive, but y is negative.
   

Example: Plot the points A(3, 5), B(—1, 4), C( 0, -3), D(-3, -2) and E(4, -2) on the same set of axes.
Solution: On plotting the points, we get:

Reflections of Points in Coordinate Axes
Reflection: Reflection is a type of transformation. It is basically a ‘flip’ of a shape over the line of reflection.
(i) Reflection in the X-axis (Mr): The general rule for a reflection in the X-axis: (x, y) becomes (x, – y)

In this case, its abscissa (x) remains the same but the sign of ordinate (y) changes.

(ii) Reflection in the Y-axis (My): The general rule for a reflection in the Y-axis: (x, y) becomes (- x, y)

Fundamentals:
Reflection transformations are widely used in computer graphics and animation. When a video game character turns around or sees its reflection in water or a mirror, the computer uses coordinate transformations and reflections to generate the image instantly.

M_y: (x, y) → (- x, y)
In this case the sign of ordinate (y) remains the same and the sign of abscissa (x) changes.
There are some invariant points, which remain unchanged after a reflection.

Example 1:
A robotics engineer programs a robot to move on a coordinate grid. Due to a sensor effect, the robot’s position appears reflected across the x-axis, and the reflected position is recorded as (8, -6).
(i) Find the actual position of the robot P
(ii) Find the coordinates of the image of P when reflected in the y-axis.
Solution:
Given that,
Coordinates of image, M_x = (8, -6)
So, M = (8, 6)
(i) Coordinates of P are (8, 6)
(ii) Under reflection in y-axis, we have, My (8, 6) = (- 8, 6) So, the coordinates of image under reflection in y-axis are (- 8, 6).

Example 2:
A large shopping mall has installed a digital navigation system based on coordinates. The positions of four shops A, B, C, and D are shown on the coordinate map of the mall. Shop C is located exactly opposite to Shop A across a mirror line placed in the mall corridor. Study the graph and answer the following questions:
(a) Write the coordinates of shops A, B, C, and D.
(b) Given that shop C is the mirror image of shop A, identify and write the equation of the line of reflection.
(c) Find the coordinates of the image of shop D when reflected in the y-axis.
(d) What do we call a point whose image remains unchanged after reflection?

Solution:
(a) Coordinates of A(3, 3), B(-2, 1), C(3, -1) and D(0,1)
(b) Midpoint of line joining A(3,3) and C(3, -1) is (3,1). So, line BD, i.e., y = 1 is the line of Reflection.
(c) Point D is (0,1).
Reflection in the y-axis changes (x, y) to (-x, y).
Since x = 0, the image remains: (0,1)
(d) A point whose image is the point itself is called an j invariant point or a fixed point.

Coordinates as Perpendicular Distances
A point (a, b) shows the position of a point on the coordinate plane.

The absolute values of the coordinates give the distances from the axes

Distance from Axes
x-coordinate (a): Distance of the point from the Y-axis, y-coordinate
(b): Distance of the point from the X-axis.

Fundamentals:
Distance is always positive. The coordinate may be positive or negative depending on the quadrant in which the point lies.

Example: Point P(a, b) lies in the third quadrant. Its perpendicular distance from the x-axis is 5 units and its perpendicular distance from the y-axis is 9 units. Find the value of \(\frac{a+b}{a-b}\).
Solution:
Distance from the x-axis = 5 ⇒ Absolute value of the y-coordinate is 5.
Distance from the y-axis = 9 ⇒ Absolute value of the x-coordinate is 9.
Since the point lies in the III quadrant (-,-), both coordinates are negative.
Therefore, the coordinates are P(-9, -5).
So, a = -9, b = – 5
Now \(\frac{a+b}{a-b}=\frac{-9-5}{-9+5}=\frac{-14}{-4}=\frac{7}{2}\)

The Concept of Slope(Gradient)
The slope (or gradient), represented by m, shows the steepness and direction of a line.
If a line makes an angle θ with the positive x-axis in the anticlockwise direction, then its slope is given by: m = tan θ

Fundamentals:
A greater absolute value of m means the line is steeper, while a slope of 0 represents a horizontal line.

The slope of a line (gradient) is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on a line. Mathematically, this is expressed as:

Fundamentals:
The slope of a line remains constant throughout the line. The steeper the line, the greater is its slope.
The slope of the line segment AB, where A is (x₁, y₁) and B is (x₂, y₂), can be calculated using the formula:
\(\frac{y_2-y_1}{x_2-x_1}\)

Properties of Slope

1. If both the y-step and x-step are positive, the line results in a positive slope. The line rises from left to right (acute angle of inclination).

2. If the y-step and x-step are opposite in sign (one positive, one negative), the line segment slants downwards as it moves from left to right, indicating a negative slope. The line falls from left to right (obtuse angle of inclination).

Lines with positive slope rising upwards are described as ‘forward sloping’ whereas lines with negative slope are characterised as ‘backward sloping’.

3. Horizontal lines (x = k, where k is any constant), which are parallel to the y-axis, possess a zero slope.

4. Vertical lines (x = k, where k is any constant), which run parallel to the y-axis, have an undefined slope.

Example: Analyse the following statements and identify which is/are incorrect.
A. The slope of a vertical line is undefined.
B. Horizontal lines have a slope of zero.
C. The slope of a line that descends from left to right is positive.
D. Lines whose slopes are negative reciprocals of each other are perpendicular.
Solution:
Statement A is correct. The slope of a vertical line is undefined.
Statement B is correct. Horizontal lines have a slope of zero, representing no vertical change.
Statement C is incorrect. A line that descends from left to right has a negative slope, not a positive slope.
Statement D is correct. Perpendicular lines indeed have slopes that are negative reciprocals of each other.

Example: A straight line with a slope of \(-\frac{3}{2}\) passes through the points P(a, 5) Q(4, 2) and R(8, b). Find the coordinates of points P and R and calculate the value of a + b.
Solution:
Given slope, m = \(-\frac{3}{2}\)
By using formula of slope, the slope of the line passing through points P(a, 5) and Q(4,2) is:
\(-\frac{3}{2}=\frac{2-5}{4-a}\)
\(-\frac{3}{2}=-\frac{3}{4-a}\)
\(\frac{1}{2}=\frac{1}{4-a}\)
4 – a = 2
a = 2
So, coordinates of P are (2, 5).
Apply similar method for the line passing through Q and R, we get
b = -4.
So, coordinates of R are (8, -4).
Now, a + b = 2 + (-4) = 2 – 4 = -2

Slopes of Parallel and Perpendicular Lines
If two lines l_a and l₂ are parallel and the gradient of l₁ is m₁, then the gradient of l₂ is also equal to m₁.
Mathematically, this relationship is expressed as: m₁ = m₂, where m₁ and m₂ are the slopes of the parallel lines l₁ and l₂, respectively.

The product of the slopes of two perpendicular lines is always -1.
Mathematically, this relationship is expressed as: m₁ × m₁ = -1.

Intercepts and Forms of the Equation of a Line
where a is the x-intercept and b is the y-intercept.

1. Understanding x-intercept as the point where the line cuts the x-axis
2. Understanding y-intercept as the point where the line cuts the y-axis
3. Converting one form of equation into another form
4. Identifying slope and intercepts directly from equations
5. Interpreting the graphical meaning of line equations

Memory Hook: L.I.N.E.
L → Locate intercepts on axes
I → Identify slope and intercepts
N → Notice different equation forms
E → Express lines algebraically

Intercepts of a Line
An intercept is the point where a line crosses the x-axis or y-axis on the coordinate plane.
y-intercept: The point where the line crosses the y-axis. Here, the x-coordinate is always 0. Form: (0, y)
x-intercept: The point where the line crosses the x-axis. Here, the y-coordinate is always 0. Form: (x, 0)

Example: Find the x-intercept and y-intercept of the line y = x + 4
y-intercept: Put x = 0
Then, y = 0 + 4 = 4
So, the y-intercept is : (0, 4)
x-intercept: Put y = 0
0 = x + 4
x = – 4
So, the x-intercept is: (-4, 0).

Different Forms of the Equation of a Line
A straight line can be represented algebraically in several ways depending on the given information.

1. General Form: Ax + By + C = 0
A straight line can be represented algebraically in the form Ax + By + C = 0, where A, B and C are constants and both A and B cannot be zero simultaneously.
Here,
Slope = \(-\frac{A}{B}\),
x-intercept = \(-\frac{C}{A}\).
y-intercept = \(-\frac{C}{B}\),

Example 1:
A city navigation system represents a straight road using the equation Ax + By + C = 0 where A < 0, B > 0, C < 0.
City planners observe that the road passes through several regions of the city shown on a coordinate map. Using the slope and intercepts of the road, determine which quadrant of the map the road can never pass through. Justify your answer mathematically.
Solution:
Given equation: Ax + By + C = 0
Slope of the line is: \(-\frac{A}{B}\)
Since A < 0 and B > 0,
\(\frac{A}{B}\) < 0 Therefore, \(-\frac{A}{B}\) > 0
So, the slope is positive. Hence, the line rises upward from left to right.
y-intercept is \(-\frac{C}{B}\)
Since C < 0 and B > 0,
\(\frac{C}{B}\) < 0 Therefore, \(-\frac{C}{B}\) > 0
So, the y-intercept is positive. The line crosses the positive side of the y-axis.
x-intercept is \(-\frac{C}{A}\)
Since C < 0 and A < 0, \(\frac{C}{A}\) > 0
Therefore, \(-\frac{C}{A}\) < 0
So, the x-intercept is negative.

Thus, the line crosses the negative side of the x-axis.
The line crosses the negative x-axis, crosses the positive y-axis and has a positive slope. Therefore, the line passes through Quadrants I, II and III. Hence, the line never passes through quadrant IV

2. Slope-Intercept form: y = mx + c
This formula is applicable when we know the slope m and the y-intercept c.
Equation: y = mx + c
The slope m represents the steepness and direction of the line, while c is the point where the line crosses the y-axis.

Fundamentals:
If line passes through the origin, then its equation will be y = mx, here c = 0.

Example: A straight line passes through the points (2, -1) and (6, 7). Determine the equation of the line in slope- intercept form.
Solution:
Given points: (2, -1) and (6, 7).
Using the slope formula,
m = \(\frac{y_2-y_1}{x_2-x_1}\)
m = \(\frac{[7-(-1)]}{6-2}=\frac{8}{4}\) = 2
Slope-intercept form is: y = mx + c
Substitute m = 2: y = 2x + c
Using the point (2, -1):
-1 = 2(2) + c
-1 = 4 + c
c = -5
Then the required equation is: y = 2x – 5

3. Intercept Form: \(\frac{x}{a}+\frac{y}{b}\) = 1
This formula is applicable when we know the x-intercept a and the y-intercept b. The required equation in
this case is: \(\frac{x}{a}+\frac{y}{b}\) = 1

The denominators represent the respective axis intercepts. Example: A straight line passes through the point (-2, -3). The line makes intercepts on both the coordinate axes that are equal in magnitude and both negative. Find the equation of the line.
Solution:
Let the equation of required line be \(\frac{x}{a}+\frac{y}{b}\) = 1
It is given that intercepts are equal in magnitude and both are negative. Then, intercept made by both the axes is -a. Then, equation of the line is:
\(\frac{x}{-a}+\frac{y}{-a}\) = 1
x + y =-1
As line passes through the point (-2, -3), so equation of line satisfies this point.
Therefore, -2 – 3 = – a
a = 5
Therefore, required equation of line is x + y = -5.

Coordinate Geometry Class 9 Notes Understanding the Lesson

Rene Descartes was a French mathematician. He introduced an idea of Carterian Coordinate System for describing the position of a point in a plane. The idea which has given rise to an important branch of Mathematics known as Coordinate Geometry.

1. Cartesian coordinate system: A system which describe the position of a point in a plane is called Cartesian system.

2. Cartesian coordinate axis: Let us draw a horizontal line XX’ and a vertical line YY’ in a plane. Both the lines intersect each other at 90°, then the plane is divided into four parts.

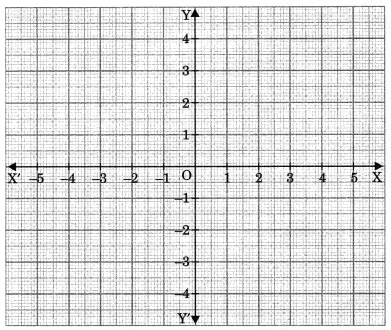
The lines XX’ and YY’ are called axes i.e., XX’ is the x-axis and YY’ is y-axis.

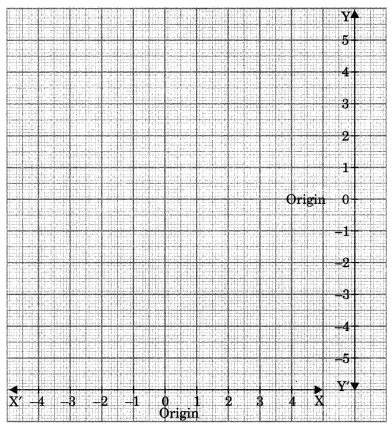
3. Origin: The point where both the axis intersect each other is known as origin.

4. Quadrant
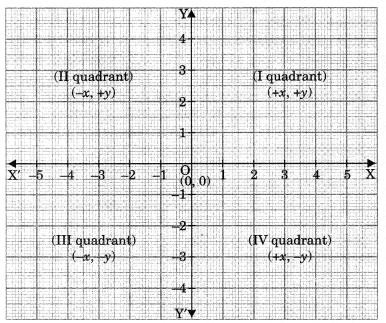
When XX’ and YY’ intersect each other then the plane is divided into four parts. These parts are called quadrants. The plane is known as Cartesian plane or XY plane.

5. Coordinate Geometry: It is a branch of geometry in which geometric problems are solved through algebra by using coordinate system.

6. Cartesian Coordinate (Rectangular Coordinate) System

In this system, the position of a point P is determined by knowing the distances from two perpendicular lines passing through the fixed point O is called origin.
The position of the point P from origin on x-axis is called x-coordinate and the position of P from origin on y-axis is called y-coordinate.

Abscissa: The distance of a point P from y-axis is called abscissa.

Ordinate: The distance of a point P from x-axis is called its ordinate.

Abscissa and ordinate together determine the position of a point in a plane, and it is called coordinates of the point. If a and b are respectively abscissa and ordinate, then the coordinates are (a, b).

Note:

• In first quadrant values of x and y are both positive.
• In second quadrant value of x is negative whereas the value of y is positive.
• In third quadrant value of x and y both are negative.
• In fourth quadrant, the value of x is positive and value ofy is negative.
• Perpendicular distance of a point from x-axis = (+)y-coordinate.
• Perpendicular distance of a point from y-axis = (+)x-coordinate.
• A point which lies on x-axis has coordinates of the form (a, 0).
• A point which lies on y-axis has coordinates of the form (0, b).
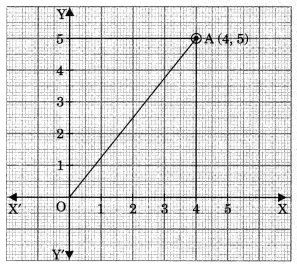
• Distance of a point P(x, y) from origin 0(0, 0) =\(\sqrt{x^{2}+y^{2}}\)
  e.g., distance of a point A(4,5) from origin, OA = \(\sqrt{4^{2}+5^{2}}\)
  \(=\sqrt{16+25}=\sqrt{41}\)units