By going through these CBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability, students can recall all the concepts quickly.
Continuity and Differentiability Notes Class 12 Maths Chapter 5
Continuity (Definition): if f be a real-valued function on a subset of real numbers and let c be a point in its domain, then f is a continuous function at e, if
![]()
Obviously, if the left-hand limit and right-hand limit and value of the function at x = c exist and are equal to each other, i.e., if
![]()
then f is continuous at x = c.
Algebra of continuous functions:
Let f and g be two real functions, continuous at x = c, then
- Sum of two functions is continuous at x = c, i.e., (f + g) (x), defined as f(x) + g(x), is continuous at x = c.
- Difference of two functions is continuous at x = c, i.e., (f – g) (x), defined as f(x) – g(x), is continuous at x = c.
- Product of two functions is continuous at x = c, i.e., (f g) (x), defined as f(x) . g(x) is continuous at x = c.
- Quotient of two functions is continuous at x = c, (provided it is defined at x = c), i.e.,
(\(\frac{f}{g}\))(x), defined as \(\frac{f(x)}{g(x)}\) [g(x) ≠ 0], is continuous at x = c.
However, if f(x) = λ, then
(a) λ.g, defined ty .g(x), is also continuous at x = c.
(b) Similr1y, if \(\frac{λ}{g}\) is defined as \(\frac{λ}{g}\) (x) = \(\frac{λ}{g(x)}\) , then \(\frac{λ}{g}\) is also continuous at x = c.
→ Differentiability: The concept of differentiability has been introduced in the lower class. Let us recall some important results.
→ Differentiability (Definition): Let f be a real function and c is a point in its domain. The derivative of f at c is defined as
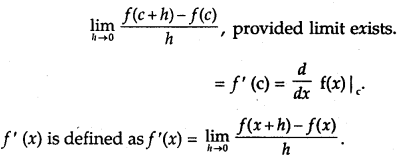
Every differentiable function is continuous.
→ Algebra of Derivatives: Let u and v be two functions of x.
- (u ± v)’ = u’ ± v’
- (uv)’ = u’v + uv’
- \(\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}\), where v ≠ 0.
→ Derivative of Composite Function: Let t be a real valued function which is a composite of two functions u and v, i.e., f = vou. Put u(x) = t and f= v(t).
∴ \(\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}\)
→ Chain Rule: Let/be a real valued function which is a composite fimction of u, v and w, i.e., f(wov)ou.
Put u(x) = t, v(t) = s and f = w(s). Then,
\(\frac{d f}{d x}=\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x}\).
→ Derivatives of Inverse Trigonometric Functions:
| Functions | Domain | Derivatives |
| Sin-1x | [- 1, 1] | \( \frac{1}{\sqrt{1-x^{2}}} \) |
| Cos-1x | [- 1, 1] | \( -\frac{1}{\sqrt{1-x^{2}}} \) |
| tan-1x | R | \( \frac{1}{1+x^{2}} \) |
| Cot-1x | R | \( -\frac{1}{1+x^{2}} \) |
| Sec-1x | (-∞, – 1] ∪ [1, ∞) | \( \frac{1}{x \sqrt{x^{2}-1}} \) |
| Cosec-1x | (-∞, – 1] ∪ [1, ∞) | \( -\frac{1}{x \sqrt{x^{2}-1}} \) |
Implicit Functions: An equation in form f(x, y) = 0, in which y is not expressible in terms of x, is called an implicit function of x and y.
Both sides of the equations are differentiated termwise. Then, from this equation, \(\frac{d y}{d x}\) is obtained. It may be noted that when a function of y occurs, then differentiate it w.r.t. y and multiply it by \(\frac{d y}{d x}\).
e.g., To find \(\frac{d y}{d x}\) from cos2 y + sin xy = 1, we differentiate it as
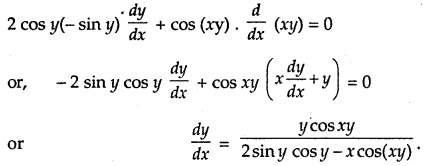
Exponential Functions:
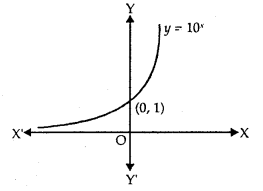
The exponential function, with positive base b > 1, is the function y = bx.
- The graph of y = 10x is shown in the figure.
- Domain = R
- Range = R+
- The point (0,1) always lies on the graph.
- It is an increasing function, i.e., as we move from left to right, the graph rises above.
- As x → – ∞, y → 0.
- \(\frac{d}{dx}\) (ax) = ax log, a, \(\frac{d}{dx}\) ex = ex.
Logarithmic Functions:
Let b> 1 be a real number. bx = a may be written as logb a = x.
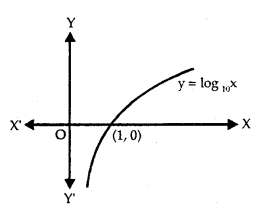
- The graph of y = log10 x is shown in the figure.
- Domain = R+, Range = R.
- It is an increasing function.
- As x → 0, y → ∞.
- The function y = ex and y = loge x are the mirror images of each other in the line y = x.
- \(\frac{d}{dx}\) (loga x) = \(\frac{1}{x}\) l0ga e, \(\frac{d}{dx}\) loge x = \(\frac{1}{x}\)
→ Other properties of Logarithm are:
- logb pq = logb p + logb q
- logb \(\frac{p}{q}\) = loga p – loga q
- logb px = x logb p – logb q
- loga b = \(\frac{\log _{a} p}{\log _{b} p}\)
→ Logarithmic Differentiation:
Whenever the functions are given in the form
- y = [u(x)]v(x) and
- y = \(\frac{u(x) \times v(x)}{w(x)}\)
take log of both sides. Simplify and differentiate, e.g.,
Let y = (cos x)sin x, log y = sin x log cos x
Differentiating, \(\frac{1}{y}\) \(\frac{dy}{dx}\) = cos x log Cos x + sin x . – \(\frac{sin x}{cos x}\)
∴ \(\frac{dy}{dx}\) = (cos x)sin y [cos x log cosx – sin x tan x].
→ Derivatives of Functions in Parametric Form: Let the given equations be x = f(t) and y = g(t), where t is the parameter. Then,
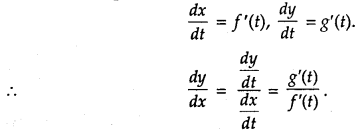
→ Second Order Derivative:
Let y = f(x), then \(\frac{dy}{dx}\) =f ‘(x).
If f ‘(x) is differentiable, then it is again differentiated.
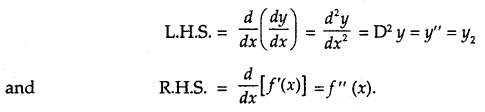
Rolle’s Theorem:
Let f: [a, b] → R be continuous on closed interval [a, b] and differentiable on open interval (a, b) such that f(a) = f(b), where a and b are real numbers, then there exists some c ∈ (a, b) such that f ‘(c) = 0.
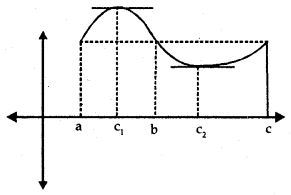
From the figure, we observe that f(a) = f(b). There exists a point c1 ∈ (a, b) such that f ‘ (c) = 0, i.e., tangent at c1 is parallel to x-axis. Similarly, f(b) = f(c) → f ‘ (c2) = 0.
→ Mean Value Theorem: Let f: [a, b] → R be a continuous function on the closed interval [a, b] and differentiable in the open interval (a, b). Then, there exists some c ∈ (a, b) such that
f ‘ (c) = \(\frac{f(b)-f(a)}{b-a}\)
Now, we know that \(\frac{f(b)-f(a)}{b-a}\) is the slope of secant drawn between A[a,f(a)] and B[b,f(b)]. We t k know that the slope of the line joining (x1, y1) and (x2, y2) is \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
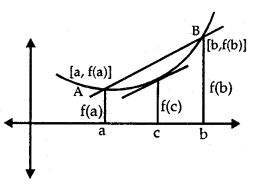
The theorem states that there is a point c ∈ (a, b), where f ‘(c) is equal to the slope of AB.
In other words, there exists a point c ∈ (a, b) such that tangent at x = c is parallel to AB.
1. CONTINUITY
(i) Left Continuity. A function ‘f ’ is left-continuous at x = c if \(\lim _{x \rightarrow c^{-}}\) f (x) = f(c).
(ii) Right Continuity. A function ‘f ’ is right-continuous at x = c if \(\lim _{x \rightarrow c^{+}}\) f (x) = f(c).
(iii) Continuity at a point. A function ‘ f ’ is continuous at x = c if
\(\lim _{x \rightarrow c^{-}}\) (x) = \(\lim _{x \rightarrow c^{+}}\) f(x) = f(c).
2. (i) Polynominal functions
(ii) Rational functions
(iii) Exponential functions
(iv) Trigonometric functions are all continuous at each point of their respective domain.
3. DIFFERENTIABILITY
(i) Left Derivative. A function ‘f ’ is said to possess left derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c-h)-f(c)}{-h}\) exists finitely.
(ii) Right Derivative. A function ‘f ’ is said to possess right derivative at x = c if
\(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.
(iii) Derivative. A function is said to possess derivative at x = c if \(\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\) exists finitely.
4. CONTINUITY AND DERIVABILITY
A real valued function is finitely derivable at any point of its domain, it is necessarily continuous at that point. The converse is not true.
5. STANDARD RESULTS
(i) \(\frac{d}{d x}\) (xn) = nxn-1 ∀ x ∈ R
(ii) \(\frac{d}{d x}\) ((ax + b)n = n(ax + b)n – 1 . a ∀ x ∈ R
(iii) \(\frac{d}{d x}(|x|)=\frac{x}{|x|}\), x ≠ 0
6. GENERAL THEOREMS
(i) The derivative of a constant is zero.
(ii) An additive constant vanishes on differentiation i.e. if f(x) = g(x) + c, where ‘c’ is any constant, then f'(x) = g'(x).
(iii) If f(x) = ag(x), then f'(x) = ag'(x), where ‘a’ is a scalar.
(iv) If f(x) = g(x) + h(x), then f'(x) = g'(x) + h'(x).
Extension.
If f(x) = a1f1 ± a2f2 ……. ± anfn(x), then :
f'(x) = a1f1‘(x) ± a2f2‘(x) ± ……. ± anfn‘(x)
(v) If f(x) = \(\frac{g(x)}{h(x)}\), then f'(x) = g(x)h'(x) + g'(x)h(x)
(vi) If f(x) = \(\frac{g(x)}{h(x)}\), then f ‘(x) = \(\frac{h(x) g^{\prime}(x)-g(x) h^{\prime}(x)}{(h(x))^{2}}\), h(x) ≠ 0.
(vii) If f(x) = \(\frac{1}{h(x)}\), then f'(x) = \(-\frac{h(x)}{[h(x)]^{2}}\), h'(x) ≠ 0
7. IMPORTANT RESULTS
(i) (a) \(\frac{d}{d x}\) (sinx) = cos x and \(\frac{d}{d x}\) (cos x) = – sin x ∀ x ∈ R
(b) \(\frac{d}{d x}\) (tan x) = sec2 x and \(\frac{d}{d x}\) (sec x) = sec x tan x ∀ x ∈ R except odd multiples of \(\frac{\pi}{2}\)
(c) \(\frac{d}{d x}\)(cot x) = – cosec2 x and \(\frac{d}{d x}\) (cosec x) = -cosec x cot x ∀ x ∈ R except even multiple of \(\frac{\pi}{2}\)
(ii)
(a) \(\frac{d}{d x}\)(sin-1x) = \(\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(b) \(\frac{d}{d x}\)(cos-1x) = \(-\frac{1}{\sqrt{1-x^{2}}}\), |x| < 1
(c) \(\frac{d}{d x}\)(tan-1x) = \(\frac{1}{1+x^{2}}\) ∀ x ∈ R
(d) \(\frac{d}{d x}\)(cot-1x) = \(-\frac{1}{1+x^{2}}\) ∀ x ∈ R
(e) \(\frac{d}{d x}\)(sec-1x) = \(\frac{1}{|x| \sqrt{x^{2}-1}}\) x > 1 or x < -1
(f) \(\frac{d}{d x}\)cosec-1x) = \(-\frac{1}{|x| \sqrt{x^{2}-1}}\), x > 1 or x < -1
(iii) (a) \(\frac{d}{d x}\) (ax) = ax loge a, a > 0
(b) \(\frac{d}{d x}\)(ex) = ex
(c) \(\frac{d}{d x}\)(loga x) = \(\frac{1}{x}\) loga e, x > 0
(d) \(\frac{d}{d x}\) (log x) = \(\frac{1}{x}\), x>0.
8. CHAIN RULE
\(\frac{d}{d x}\) (f(g(x)) = f'(g(x)).g'(x)
9. PARAMETRIC EQUATIONS
\(\frac{d y}{d x}=\frac{d y / d t}{d x / d t}\), \(\frac{d x}{d t}\) ≠ 0
Or \(\frac{d y}{d x}=\frac{d y}{d t} \times \frac{d t}{d x}\)
10.MORE RESULTS
(i) \(\frac{d y}{d x}=\frac{1}{\frac{d x}{d y}}\)
(ii) \(\frac{d y}{d x} \times \frac{d x}{d y}=1\)
11. ROLLE’S THEOREM
If a function f(x) is :
(i) continuous in [a, b]
(ii) derivable in (a, b)
(iii) f (a) = f (b), then there exists at least one point ‘c’ in (a, b) such that f’ (c) = 0.
12. LAGRANGE’S MEAN VALUE THEROEM (LMV THEOREM OR MV THEOREM)
If a function f(x) is :
(i) continuous in [a, b]
(ii) derivable in (a, b), then there exists at least one point ‘c’ in (a, b) such that \(\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)\)