By going through these CBSE Class 12 Chemistry Notes Chapter 2 Solutions, students can recall all the concepts quickly.
Solutions Notes Class 12 Chemistry Chapter 2
Solution: It is a homogeneous mixture of two or more components whose composition may be varied within limits. The component present in the largest quantity is known as Solvent. One or more components present in the solution other than the solvent are called Solutes. Solutions consisting up of two components only are called Binary Solutions.
In all there are 9 types of solutions:
Expressing Concentration of Solutions
1. Mass Percentage (W/W):
Mass of the comp, in solution
Mass % of a component= \(\frac{\text { Mass of the comp. in solution }}{\text { Total mass of solution }}\) × 100
2. Volume Percentage (V/V):
Volume % of a component = \(\frac{\text { Volume of the component }}{\text { Total volume of solution }}\) × 100
The total volume of the solution
3. Mass by volume percentage (W/V):
It is the mass of solute dissolved in 100 mL of the solution.
4. Parts per million (ppm):
Parts per million
\(\frac{\text { No. of parts of the component }}{\text { Total no. of parts of all components of the solution }}\) × 106
5. Mole Fraction:
Mole fraction of a component (x) = \(\frac{\text { No. of moles of the component }}{\text { Total no. of moles of all components }}\)
If there are 2 components in a binary solution of A and B.
xA = \(\frac{n_{A}}{n_{A}+n_{B}}\)
xB = \(\frac{n_{B}}{n_{A}+n_{B}}\)
[where nA and nB are the no. of moles of A and B respectively]
xA + xBB = 1
For a solution containing i no. of components
xi = \(\frac{n_{i}}{n_{1}+n_{2}+\ldots n_{i}}=\frac{n_{i}}{\Sigma n_{i}}\)
6. Molarity (M): Molarity is defined as the no. of moles of the solute dissolved in one litre (or one cubic decimetre) of solution.
Molarity (M) = \(\frac{\text { Moles of solute }}{\text { Volume of solution in litre }}\)
= \(\frac{\text { Strength of solute per litre of solution }}{\text { Molar mass of the solute }}\)
7. Molality (m): It is defined as the no. of moles of the solute per 1000 g [l kg] of the solvent.
Molality (m) = \(\frac{\text { Moles of solute }}{\text { Mass of solvent in } \mathrm{kg}}\)
= \(\frac{\text { Strength of the solute per } 1000 \mathrm{~g} \text { of solvent }}{\text { Molar mass of the solute }}\)
Mass %, ppm, mole fraction and molality are independent of temperature, whereas molarity depends upon temperature.
Solubility: The solubility of a substance is its maximum amount that can be dissolved in a given amount of solvent at a given temperature. It depends upon the nature of solute and solvent as well as temperature and pressure.
→ Solubility of a solid in a Liquid: In general, polar solutes dissolve in polar solvents and non-polar solutes in non-polar solvents. Like Dissolves Like. In general, a solute dissolves in a solvent if the intermolecular interactions are similar.
Solute + Solvent → Solution
→ Saturated Solution: A solution is said to be saturated if no more of the solute can be dissolved in it at a particular temperature and pressure.
→ Effect of Temperature on Solubility: The solubility of a solid in a liquid is significantly affected by temperature changes. If the process of dissolution in a nearly saturated solution is endothermic (Δsol H > 0), the solubility should increase with rising temperature and if it is exothermic (Δsol H < 0), the solubility should decrease.
→ Effect of Pressure: Pressure does not have any significant effect on the solubility of solids in liquids. It is so because solids and liquids are highly incompressible and practically remain unaffected by changes in pressure.
→ Solubility of a Gas in a Liquid: The solubility of gases in liquids is greatly affected by pressure and temperature. The solubility of gases increases with the increase of pressure.
Henry’s Law: It states, “At a constant temperature, “The solubility of a gas in a liquid is directly proportional to the pressure of the gas.”
Dalton also concluded, “The solubility of a gas in a liquid solution is a function of the partial pressure of the gas.”
In other words, “The mole fraction of the gas in the solution is proportional to the partial pressure of the gas over the solution.”
The most commonly used form of Henry’s law states “The partial pressure of the gas in the vapour phase (p) is proportional to the mole fraction of the gas (x) in the solution.”
p = KHx
Where KH is Henry’s law constant and it is a function of the nature of the gas.
Solubility of a gas in a liquid decreases with an increase in temperature. It is due to this reason that aquatic species like fish are more comfortable in cold waters rather than warm water.
Applications of Henry’s Law:
- Pressure is kept high to increase the solubility of CO2 in soft drinks.
- Deep-sea divers experience bends or decompression sickness due to greater solubility of N2 and O2 in blood. O2 is dissolved in the blood and other body fluids and N2 will remain dissolved and will form bubbles when the diver comes to the atmospheric pressure. Hence N2 in compressed air is’ replaced by He which is much less soluble in biological fluids.
- In the function of lungs: Due to the partial pressure of O2 being high when it enters the lungs, it combines with haemoglobin to form oxyhaemoglobin. The partial pressure of O2 in tissues is low. Hence O2 is released from oxyhaemoglobin which is utilised for functions of cells
Vapour Pressure of Liquid-Liquid Solutions: In a binary solution of two volatile liquids in a closed vessel, let Ptotal, p1 and p2 denote total vapour of the solution, partial vapour pressures of the two compounds and x1 and x2 their mole fractions, then according to Raoult’s Law.
p1 ∝ x1
and p1 = p1° × x1
where p1° is the V.P. of pure component 1
Similarly p2 = p2° × x2
where p2° is the V.P. of pure component 2
[Raoult’s Law states “For a solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.”]
Now according to Dalton’s law of partial pressures.
Ptotal = P1 + P2
= p1° + p2° x2
= (1 – x2)p° + x2 p°
= P1° + ( P2° – P1° )x2.
Following conclusions can be drawn from the above equations
- Total vapour pressure over the solution can be related to the mole fraction of any one component.
- Total vapour pressure over the solution varies linearly with the mole fraction of component 2.
- Depending upon the vapour pressure of the pure components 1 and 2, total vapour pressure over the solution decreases or increases with the increase of the mole fraction of component 1.
Assuming component 1 to be less volatile than component 2, the minimum value of ptotal is p° and the maximum value p° (i.e. p° < p° ), a graph can be drawn between the mole fraction and their vapour pressures in solution.
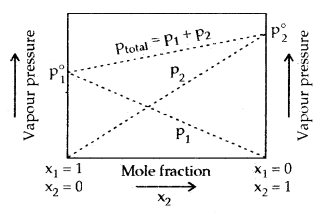
The composition of the vapour phase in equilibrium with the solution is determined by the partial pressure of the components. If y1 and y2 are the mole fractions of the components 1 and 2 in the vapour phase, then, using Dalton’s law of partial pressures
P1 = y1 Ptotal
P2 = y2 Ptotal
In general Pi = yi Ptotal
It can be concluded: At the equilibrium vapour phase will be always richer in the component which is more volatile.
Raoult’s law is a special case of Henry’s law
According to Raoult’s law pi = xi pi°
According to Henry’s Law p = KH × x
Here only the proportionality constant KH differs from pi°. Thus Raoult’s law becomes a special case of Henry’s law in which KH becomes equal to Pi°.
Ideal and Non-Ideal Solution: A solution that obeys Raoult’s Law at all concentrations and at all temperatures is called an Ideal Solution. Herein the magnitude of solute-solvent interactions is the same as the magnitude and solvent of the solute-solute interaction- solvent interactions magnitude in the two components.
For ideal solutions enthalpy on mixing remains the same,
i.e., ΔHMix = 0
For such solutions, there is no change in volume on mixing the two components
i.e., ΔVMix = 0
Non-Ideal Solutions are those which do not obey Raoult’s Law: For such solutions, the magnitude of solute-solvent interactions is either greater than or less than the magnitude of solute-solute or solvent-solvent interactions in the pure components.
Additionally, during solution formation either heat is evolved or absorbed.
i.e.; ΔHMix = +Ve
or
ΔHMix = -Ve [or ΔHMix ≠ 0]
Moreover, there is a volume change in mixing
ΔHMix ≠ 0
Examples of ideal solutions:
- n-hexane + n-heptane
- Benzene + Toluene
- Chlorbenzene + bromobenzene
- CCl4 + SiCl4
- CH3OH + C2H5OH.
Examples of Non-ideal solutions:
| With Positive deviations | With Negative deviations |
| 1. acetone and ethanol | 1. Water + HCl |
| 2. Acetone + Benzene | 2. Water + HNO3 |
| 3. Acetone + CCl4 | 3. CHCl3 and acetone |
| 4. Benzene + CCl4 | 4. Acetic acid + pyridine |
| 5. Water + ethyl alcohol | 5. Acetone + aniline |
| 6. Cyclohexane + ethanol | 6. Benzene + CHCl3 |
Colligative Properties: These properties depend only on the number of solute particles, but not on the nature of the solute.
They are
- Relative lowering of vapour pressure
- Elevation in boiling points
- Depression in freezing point
- Osmotic pressure.
1. Relative lowering of vapour pressure: The relative lowering of the vapour pressure of a dilute solution (which, for all intents and purposes, is an ideal solution) is equal to the mole fraction of the solute at a given temperature.
If xA = Mole fraction of the solvent
xB = Mole fraction of the solute
PA = Vapour pressure of the pure solvent
PB = Vapour pressure of the solution
\(\frac{P_{A}^{\circ}-P_{A}}{P_{A}^{\circ}}\) is called the relative lowering of vapour pressure
WA = Mass of comp. A
MA = M. mass of comp. A
WB = Mass of comp. B
MB = M. mass of comp. B
From relative lowering in vapour pressure, the molar mass of solute can be calculated as:
MB = \(\frac{W_{\mathrm{B}} \times \mathrm{M}_{\mathrm{A}}}{\mathrm{W}_{\mathrm{A}} \times \frac{\mathrm{P}_{\mathrm{A}}^{\circ}-\mathrm{P}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{A}}^{\circ}}}\)
2. Elevation in boiling: The boiling point of a liquid may be defined as the temperature at which its vapour pressure becomes equal to atmospheric pressure. When a non-volatile solute is added to a solvent, the solution boils at a higher temperature than the pure solvent.
If Tb° is the boiling point of the pure solvent and Tb is the boiling point of the solution, then elevation in boiling point,
ΔTb = Tb – Tb° = Kb × m
where m is the molality of the solution and Kb is molal elevation constant or ebullioscopic constant of the solvent.
Molal elevation in boiling point is defined as the elevation in boiling point produced when 1 mole of a solute is dissolved in 1000 g of the solvent.
The molar mass of the solute can be calculated from the elevation in boiling point as
MB = \(\frac{\mathrm{K}_{\mathrm{b}} \times \mathrm{W}_{\mathrm{B}} \times 1000}{\Delta \mathrm{T}_{\mathrm{b}} \times \mathrm{W}_{\mathrm{A}}}\)
The molar elevation constant is expressed as
Kb = \(\frac{\mathrm{RT}_{\mathrm{b}}^{\circ} \mathrm{M}}{\Delta \mathrm{H}_{\mathrm{vap}} \times 1000}\)
or
= \(\frac{\mathrm{RT}_{\mathrm{b}}^{\circ}}{\Delta \mathrm{h}_{\mathrm{vap}} \times 1000}\)
where Tb° is the boiling point of the solvent, M is the molar mass of the solvent, R is gas constant and ΔHvap is the enthalpy of vaporisation of the pure solvent. Δhvap is the enthalpy of vaporisation per gram as
Δhvap = \(\frac{\Delta \mathrm{H}_{\mathrm{vap}}}{\mathrm{M}}\)
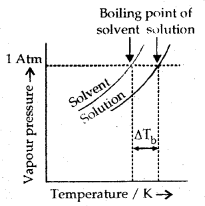
The vapour pressure curve of the solution lies below the curve for pure solvent. The diagram shows that ΔTb denotes the elevation of the boiling point of a solvent in the solution.
3. Depression in freezing point: The freezing point of a liquid may be defined as the temperature at which solid and the liquid states of the same substance have the same vapour pressure. When a non-volatile solute is added to a solvent, the freezing point of the solution is always less than the freezing point of the pure solvent.
If Tf° is the freezing point of the pure solvent and Tf is the freezing point of the solution, then depression in freezing point,
ΔTf = Tf° – Tf = Kf. m
where Kf = molal depression constant or cryoscopic constant
m = molality of the solution
Molal depression constant (Kf) is the depression in freezing point produced when 1 mole of solute is dissolved in 1000 g of the solvent.
Molar mass of solute from depression in freezing point may be calculated as
MB = \(\frac{\mathrm{K}_{\mathrm{f}} \times \mathrm{W}_{\mathrm{B}} \times 1000}{\Delta \mathrm{T}_{\mathrm{f}} \times \mathrm{W}_{\mathrm{A}}}\)
The molal depression constant is
Kf = \(\frac{\mathrm{RT}_{\mathrm{f}}^{\circ} \mathrm{M}}{\Delta \mathrm{H}_{\mathrm{t}} \times 1000}\)
or
= \(\frac{R T_{f}^{\circ} f}{\Delta h_{f} \times 1000}\)
where R is gas constant, Tf° is the freezing point of the solvent, M is the molar mass and ΔHf is the enthalpy of fusion of the solvent, Δhf is the enthalpy of fusion per gram and is
Δhf = \(\frac{\Delta \mathrm{H}_{\mathrm{f}}}{\mathrm{M}}\)
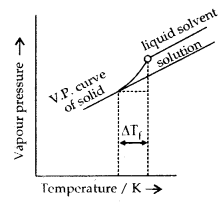
Diagram showing ΔTf depression of the freezing point of a solvent in a solution.
4. Osmotic pressure: The phenomenon of the flow of solvent through a semi-permeable membrane from pure solvent to the solution ‘ is called osmosis. The osmotic pressure may be defined as the excess pressure which must be applied to a solution to prevent the passage of solvent into it through a semi-permeable membrane. The osmotic pressure for a solution (TC) is
π = c RT
where c is the molar concentration, R is the gas constant and T is the temperature.
Molar mass of a solute from the osmotic pressure may be calculated as:
MB = \(\frac{W_{B} R T}{V \times \pi}\)
→ Isotonic solutions: The solutions having the same osmotic pressure are called isotonic.
→ Abnormal Molar Masses: Colligative properties depend upon the number of solute particles. Therefore, in case of those solutions which undergo dissociation or association in solution, the colligative properties will be different
Van t Hoff factor = \(\frac{\text { Observed colligative property }}{\text { Normal value of colligative property }}\)
= \(\frac{\pi_{\text {obs }}}{\pi_{\text {nor }}}=\frac{\Delta \mathrm{T}_{\mathrm{b}(\mathrm{obs})}}{\Delta \mathrm{T}_{\mathrm{b}(\mathrm{nor})}}=\frac{\Delta \mathrm{T}_{\mathrm{f}(\mathrm{obs})}}{\Delta \mathrm{T}_{\mathrm{f}(\text { nor })}}\)
→ The principle of measuring osmotic pressure: The pressure in excess of atmospheric pressure that must be applied to the solution to prevent it from rising in the tube is the osmotic pressure. This will also be equal to”hydrostatic pressure of the liquid column of height, h.
Since colligative property is inversely proportional to the molar mass of the solute, therefore,
i = \(\frac{\text { Normal molar mass }}{\text { Observed molar mass }}\)
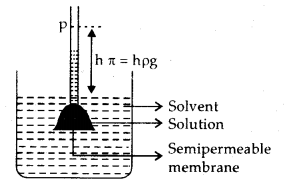
∴ Observed Osmotic pressure, π = i × \(\frac{n}{V}\) RT
Observed elevation in B.Pt. ΔTb = i × Kb × m
Observed depression in F.Pt. ΔTf = i × Kf × m where m = molality of the solution
Reverse Osmosis and water purification: The direction of Osmosis can be reversed if a pressure larger than the osmotic pressure is applied to the solution, side. That is, now the pure solvent flows out of the solution tiìrough the semi-permeable membrane (SPM).
This phenomenon is called Reverse Osmosis and is of great utility. Reverse osmosis is used for the Desalination of seawater. The pressure required for reverse osmosis is quite high and a workable porous membrane is a film of cellulose acetate placed over suitable support. Cellulose acetate is permeable to water but impermeable to impurities and ions present in seawater.
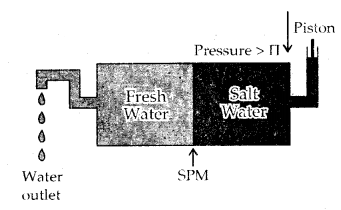
Reverse osmosis occurs when a pressure larger than the osmotic pressure is applied to the solution.