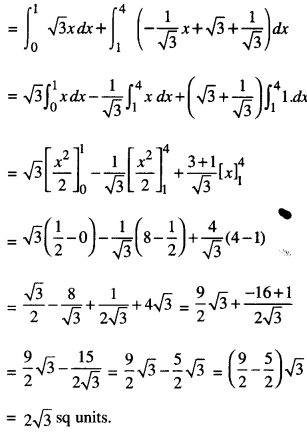Here we are providing Class 12 Maths Important Extra Questions and Answers Chapter 8 Applications of the Integrals. Class 12 Maths Important Questions are the best resource for students which helps in Class 12 board exams.
Class 12 Maths Chapter 8 Important Extra Questions Applications of the Integrals
Applications of the Integrals Important Extra Questions Very Short Answer Type
Question 1.
Find the area of region bounded by the curve y = x2 and the line y = 4.
Answer:
\(\frac { 32 }{ 2 }\) sq. units.
Question 2.
Find the area bounded by the curve y = x3, x = 0 and the ordinates x = -2 and x = 1.
Answer:
\(\frac { 17 }{ 4 }\) sq. units.
Question 3.
Find the area bounded between parabolas y2 = 4x and x2 = 4y.
Answer:
\(\frac { 16 }{ 3 }\) sq. units.
Question 4.
Find the area enclosed between the curve y = cos x, 0 ≤ x ≤ \(\frac{\pi}{4}\) and the co-ordinate axes.
Answer:
\(\frac { 1 }{ 2 }\) sq. units.
Question 5.
Find the area between the x-axis curve y = cos x when 0≤ x < 2.
Answer:
4 sq. units
Question 6.
Find the ratio of the areas between the centre y = cos x and y = cos 2x and x-axis for x = 0 to
x = \(\frac{\pi}{3}\)
Answer:
2:1.
Question 7.
Find the areas of the region:
{(x,y): x2 + y2 ≤ 1 ≤ x + 4}
Ans.
\(\frac{1}{2}\) (π – 1) sq. units.
Applications of the Integrals Important Extra Questions Long Answer Type 2
Question 1.
Find the area enclosed by the circle:
x2 + y2 = a2. (N.C.E.R.T.)
Solution:
The given circle is
x2 + y2 = a2 ………….(1)
This is a circle whose centre is (0,0) and radius ‘a’.
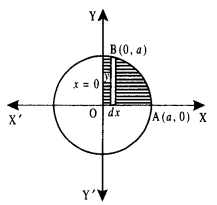
Area of the circle=4 x (area of the region OABO, bounded by the curve, x-axis and ordinates x = 0, x = a)
[ ∵ Circle is symmetrical about both the axes]
= 4 \(\int_{0}^{a}\) ydx [Taking vertical strips] o
= \(4 \int_{0}^{a} \sqrt{a^{2}-x^{2}} d x\)
[ ∵ (1) ⇒ y = ± \(\sqrt{a^{2}-x^{2}}\)
But region OABO lies in 1st quadrant, ∴ y is + ve]
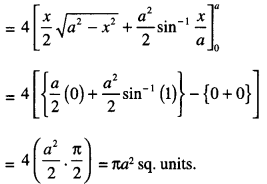
Question 2.
Using integration, find the area of the region in the first quadrant enclosed by the x-axis, the liney = x and the circle x2 + y2 = 32. (C.B.S.E. 2018)
Solution:
We have :
y = x …(l)
and x2 + y2 = 32 …(2)
(1) is a st. line, passing through (0,0) and (2) is a circle with centre (0,0) and radius 4√2 units. Solving (1) and (2) :
Putting the value of y from (1) in (2), we get:
x2 + x2 = 32
2x2 = 32
x2 = 16
x = 4.
[∵ region lies in first quadrant]
Also y = 4
Thus the line (1) and the circle (2) meet each other at B (4,4), in the first quadrant.
Draw BM perp. to x – axis.
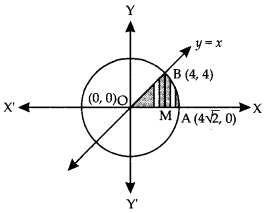
∴ Reqd. area = area of the region OMBO + area of the region BMAB …(3)
Now, area of the region OMBO
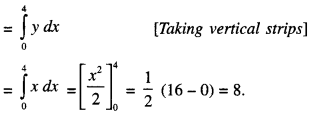
Again, area of the region BMAB
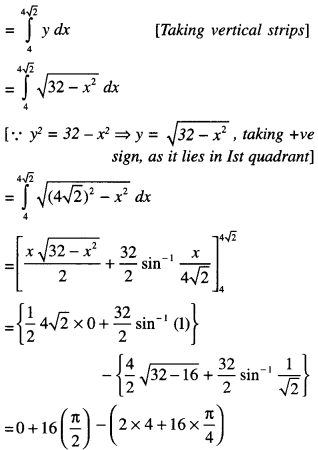
= 8π – (8 + 4π) = 4π – 8
∴ From (3),
Required area = 8 + (4π – 8) = 4π sq.units.
Question 3.
Find the area bounded by the curves y = √x , 2y + 3 = Y and Y-axis. (C.B.S.E. Sample Paper 2018-19)
Solution:
The given curves are
y = √x ………….(1)
and 2y + 3 = x …(2)
Solving (1) and (2), we get;
\(\sqrt{2 y+3}\) = y
Squaring, 2y + 3 = y2
⇒ y22 – 2y – 3 = 0
⇒ (y + 1)(y-3) = 0 ⇒ y = -1, 3
⇒ y = 3 [∵ y > 0]
Putting in (2),
x = 2(3) + 3 = 9.
Thus, (1) and (2) intersects at (9, 3).
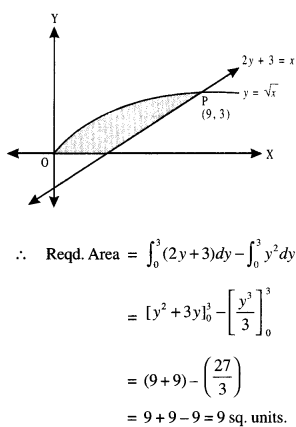
Question 4.
Find the area of region:
{(x,y): x2 + y2 < 8, x2 < 2y}. (C.B.S.E. Sample Paper 2018-19)
Solution:
The given curves are ;
x2 + y2 = 8 ………… (1)
x2 = 2y ………… (2)
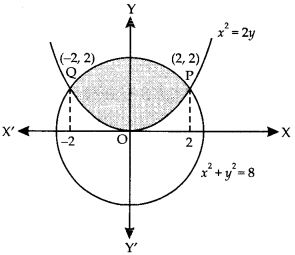
Solving (1) and (2):
8 – y2= 2y
⇒ y2 + 2y – 8 = 0
⇒ (y + 4)(y – 2) = 0
= y = -4,2
⇒ y = 2. [∵ y > 0]
Putting in (2), x2 = 4
⇒ x = -2 or 2.
Thus, (1) and (2) intersect at P(2, 2) and Q(-2, 2).
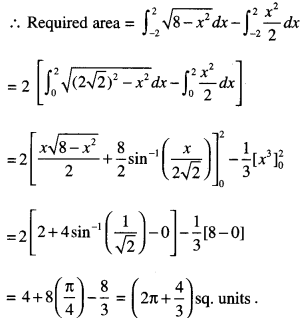
Question 5.
Using integration, find the area of the region enclosed between the two circles:
x2 + y2 = 1 and (x – 1)2 + y2 = 1. (C.B.S.E. 2019 C, C.B.S.E. 2019)
Solution:
The given circles are x2 + y2 =1 …(1)
and (x – 1)2 + y2 = 1
(1) is a circle with centre (0,0) and radius 1.
(2) is a circle with centre (1,0) and radius 1.
Solving (1) and (2):
(2)-(1) gives: -2x + 1 =0 ⇒ x = \(\frac { 1 }{ 2 }\).
Putting in (1), \(\frac { 1 }{ 4 }\) + y2 = 1
y2 = \(\frac { 3 }{ 4 }\)
⇒ y = ± \(\frac{\sqrt{3}}{2}\)
Thus, the circles intersect at A (\(\frac{1}{2}, \frac{\sqrt{3}}{2}\)) and B(\(\frac{1}{2},-\frac{\sqrt{3}}{2}\))
Reqd. area = 2 (shaded area)
= 2 (area (OAL) + area (ALC))
Question 6.
Using integration, find the area of the region: {(x, y); 9x2 + 4y2 ≤ 36,3x + 2y ≥ 6}. (C.B.S.E. 2019(C))
Solution:
We have: 9x2 + 4y2 = 36
\(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1 …(1) ,
which is an upward ellipse
and 3x + 2y = 6 =» \(\frac{x}{2}+\frac{y}{3}\) = 1 …(2),
which is a st. line.
Reqd. area is the shaded area, as shown in the figure:
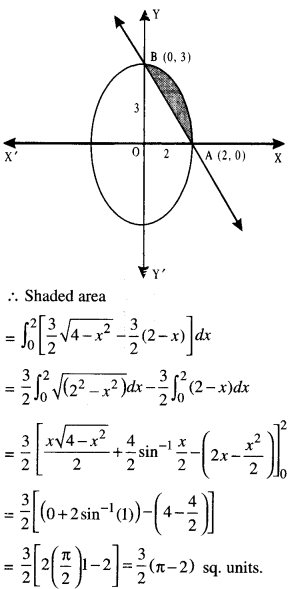
Question 7.
Using the method of integration, find the area of the region bounded by the lines:
3x – 2y + 1 = 0,2x + 3y – 21 = 0 and x – 5y + 9 = 0. (A.I.C.B.S.E. 2019, C.B.S.E. 2012)
Solution:
Let the sides AB, BC and CA of ΔABC be:
3x – 2y + 1 = 0 …(1)
2x + 3y – 21 = 0 …(2)
and x – 5y + 9 = 0 …(3) respectively.
Solving (3) and (1), we get A as (1,2).
Solving (1) and (2), we get B as (3,5).
Solving (2) and (3), we get C as (6,3).
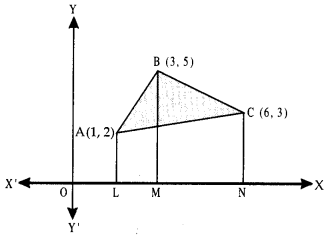
Now ar (ΔABC) = ar (trap ALMB) + ar (trap BMNC) – ar (trap ALNC)
= \(\frac{65}{10}\) = 6.5sq . units.
Question 8.
Find the area lying above the x-axis and included between the circle x2 + y2 = Sir and the parabola y2 = 4x. (N.C.E.R. I; C.B.S.E. 2019,19 C)
Solution:
The given circle is x2 + y2 – 8x = 0
i.e. (x-4)2 + y2 = 16 ….. (1)
It has centre (4,0) and radius 4 units.
The given parabola is y2 = 4x ….(2)
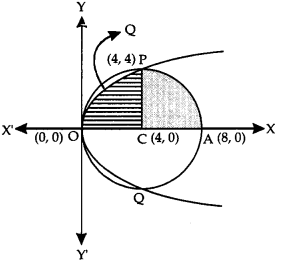
Solving (1) and (2) :
x2 – 8x + 4x = 0 =
⇒ x2 – 4x = 0
⇒ x(x-4) = 0
⇒ x = 0,4.
When x = 0,y = 0.
When x = 4,y2 = 16
⇒ y = ±4.
Thus (1) intersects (2) at O (0, 0) and P (4, 4) above the x-axis.
∴ Area of the region OC APQO
= Area of the region OCPQO + Area of the region C APC
= \(\int_{0}^{4} y_{1} d x+\int_{4}^{8} y_{2} d x\)
where yv y2 are ordinates of points on (2) and (1) respectively.
= \(\int_{0}^{4} \sqrt{4 x} d x+\int_{4}^{8} \sqrt{4^{2}-(x-4)^{2}} d x\)
[∵ Thinking +ve values as region lies above x-axis]
[Putting x-4 = t in 2nd integral so that dx = dt. When x = 4, t = 0; when x – 8, t = 4]
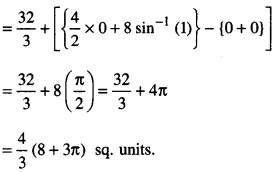
Question 9.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9. (Outside Delhi 2019)
Answer:
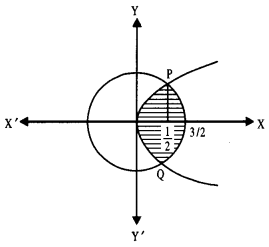
To find the points of intersection of the curves.
y2 = 4x …(1)
and 4x2 + 4y2 = 9 …(2)
From (1) and (2),
4x2 + 16x = 9
⇒ 4x2+ 10x – 9 = 0.
Solving, x = \(\frac { 1 }{ 2 }\)
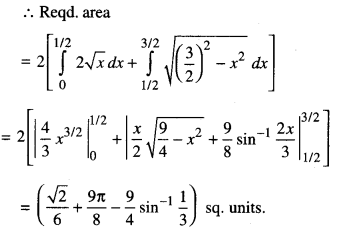
Question 10.
Using integration, find the area of the region bounded by the iiney = 3x +2, the x-axis and the ordinates x = -2 and x = 1. (Outside Delhi 2019)
Answer:
The region is as shown in the figure.
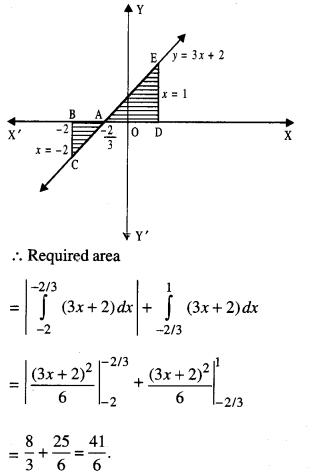
Question 11.
Using integration, find the area of the region:
{(x,y): x2 + y2 ≤ 1, x + y ≥ 1 x ≥ 0, y ≥ 0}
Answer:
We have: x2 + y2 = 1 …(1)
and x + y = 1 …(2)
Solving (1) and (2), x2 + (1 – x)2 = 1 ⇒
2x2 – 2x = 0
2x(x-1) = 0
x = 0
x = 1.
or
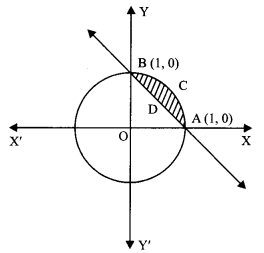
Required area = Shaded area ACBDA
= ar(OACBO – ar(OADBO)
Question 12.
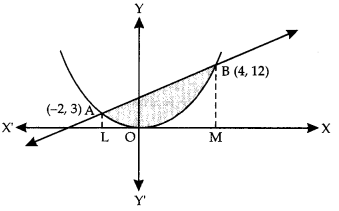
Find the area enclosed between the parabola 4y = 3x2and the straight line 3x – 2y +12 = 0.
(A.I.C.B.S.E. 2017)
Answer:
The given parabola is 4y – 3x2
i.e. x2 = \(\frac{4 y}{3}\)…(1),
which is an upward parabola.
The given line is 3x – 2y + 12 = 0 ……….. (2)
Solving (1) and (2) :
From(1), y = \(\frac{3 x^{2}}{4}\) …(3)
Putting in (2),
3x – 2(\(\frac{3 x^{2}}{4}\)) + 12 = 0
x – \(\frac{x^{2}}{4}\) + 4 = 0
⇒ x2 – 2x – 8 =0
⇒ (x-4)(x + 2)-0
⇒ x = – 2, 4.
When x = -2, then from (3),
y = \(\frac { 3 }{ 4 }\)(4) = 3.
When x = 4, then from (3),
y = \(\frac { 3 }{ 4 }\)(16) = 12.
Thus parabola (1) and line (2) meet each other at A (-2, 3) and B (4,12).
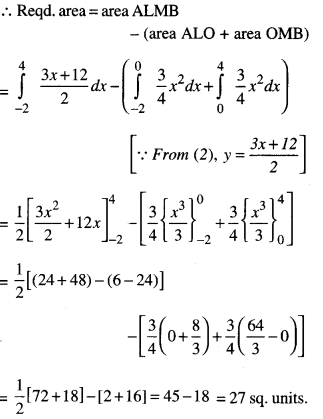
Question 13.
Using integration, find the area of the region :
{(x, y : |x-1| ≤ y ≤ \(\sqrt{5-x^{2}}\)} (C.B.S.E. 2010)
Or
Sketch the region bounded by the curves:
y= \(\sqrt{5-x^{2}}\) and y = |x-1|and find its area, using integration.
(A.I.C.B.S.E. 2015)
Solution:
The given curves are : x2 + y2 = 5
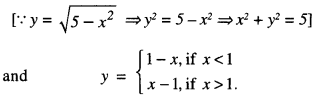
The reqd. region is shown as shaded in the following figure:
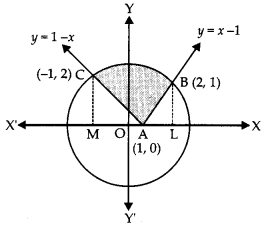
y =x-1 meets x2 + y2 = 5 at B(2,1).
y = 1-x meets x2 + y2 = 5 atC(-1,2)
y = x -1 and y = 1 -xmeet at A(1, 0).
Reqd. area = ar (MCBLM) – ar (CMAC) – ar (ALBA)
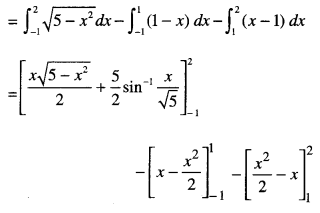
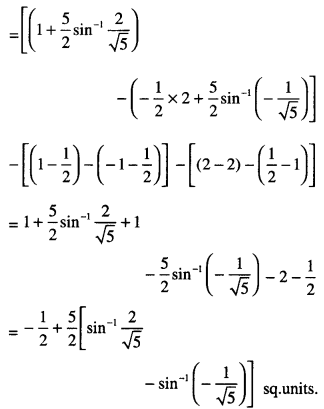
Question 14.
Using integration, find the area of the triangle formed by positive x-axis and tangent and
normal to the circle x2 + y2 = 4 at (1, 73). (C.B.S.E. 2015)
Solution:
The given circle is
x2 + y2 = 4 ……. (1)
Diff. w.r.t. x,
2x + 2y \(\frac{d y}{d x}\) = 0
\(\frac{d y}{d x}\) = \(\frac{-x}{y}\)
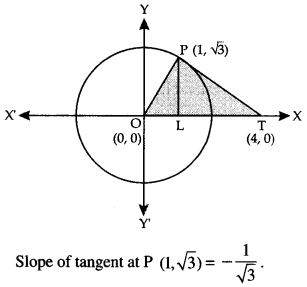
Slope of normal at P (1, √3) =√3 .
∴ The equation of the tangent at P is :
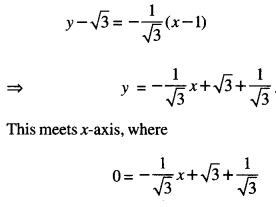
⇒ 0 = -x + 3 + 1
⇒ x = 4.
Thus T is (4,0).
The equation of the normal at P is :
y – √3= √3(x-l)
⇒ y = √3x.
This meets x-axis i.e. y = 0, where x = 0.
Thus O is (0,0).
Now ar (ΔOPT) = ar (OPL) + ar (PLT)