Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 15 Waves. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.
Class 11 Physics Chapter 15 Important Extra Questions Waves
Waves Important Extra Questions Very Short Answer Type
Question 1.
In a resonance tube, the second resonance does not occur exactly at three times the length at the first resonance. Why?
Answer:
This is due to the end correction.
Question 2.
What is the nature of ultrasonic waves and what is their frequency?
Answer:
Ultrasonic waves are longitudinal waves in nature and have frequencies greater than 20 k Hz.
Question 3.
Is the principle of superposition wave valid in the case of electromagnetic (e.m.) waves?
Answer:
Yes.
Question 4.
A rod is clamped at one end and it is hit by a hammer at the other end
(a) at a right angle to its length
(b) along the length.
What types of waves are produced in each case?
Answer:
(a) Transverse waves
(b) Longitudinal waves.
Question 5.
Why do not we hear beats if the frequency of ìwo sounds is widely different?
Answer:
The beats can’t be heard as separate due to the persistence of hearing if the difference in frequencies is more than 10 Hz.
Question 6.
What causes the rolling sound of thunder?
Answer:
The multiple reflections of the sound of lighting results in the rolling ’ sound of thunder.
Question 7.
A tuning fork produces resonance in a closed pipe. But the ‘ same tuning fork is unable to, produce resonance in an open organ pipe of equal length. Why?
Answer:
It is because the fundamental frequencies of open and closed organ pipes of the same length are different,
Question 8.
Thick and big curtains are preferred in a big hall. Why?
Answer:
To increase the absorption and decrease the reverberation time and hence making the sound uniform,
Question 9.
Why female voice is sweeter than that of a man?
Answer:
This is because the frequency of a lady’s voice is greater than that of a man’s voice.
Question 10.
The frequency of the fundamental note of a tube closed at one end is 200 Hz. What will be the frequency of the fundamental note of a similar tube of the same length but open at both ends?
Answer:
400 Hz.
Question 11.
A wave transmits energy. Can it transmit momentum?
Answer:
Yes.
Question 12.
By how much the wave velocity increases for 1°C rise of temperature?
Answer:
Wave velocity increases by 0.61 ms for 1°C rise of temperature.
Question 13.
Why the sound heard is more in carbon dioxide than in air?
Answer:
This is because the intensity of sound increases with the increase in the density of the medium.
Question 14.
What is the relation between path difference and phase difference?
Answer:
Phase difference = \(\frac{2π}{λ}\) × path difference.
Question 15.
Is it possible to have interference between the waves produced by two violins? Why?
Answer:
No. This is because the sounds produced will not have a constant, phase difference.
Question 16.
The windowpanes of houses sometimes get cracked due to some explosion at a large distance. Which waves are responsible for this?
Answer:
Shockwaves.
Question 17.
Why the velocity of sound is generally greater in solids than in gases?
Answer:
This is because \(\frac{E}{ρ}\) for solids is much greater than for gases.
Question 18.
An observer places his ear at the end of a long steel pipe. He can hear two sounds when a workman hammers the other end of the pipe. Why?
Answer:
This is because the sound is transmitted both through air and medium.
Question 19.
Why a stationary wave is so named?
Answer:
A stationary wave is so named because there is no net propagation of energy. .
Question 20.
How do we identify our friends from his voice while sitting in a dark room?
Answer:
The quality of sound helps us to identify the sound.
Question 21.
Why bells are made of metal and not of wood?
Answer:
This is because the wood has high damping.
Question 22.
What is the nature of light waves?
Answer:
Electromagnetic waves.
Question 23.
When a vibrating tuning fork is moved speedily towards a wall, beats are heard. Why?
Answer:
This is due to the difference in the frequency of the incident wave and the apparent frequency of the reflected wave.
Question 24.
The weight suspended from a sonometer wire is increased by a factor of 4. Will the frequency of the wire be increased exactly by a factor of 2? Justify your answer.
Answer:
No. There will be a slight increase in the length of the wire. So the frequency shall become slightly less than double.
Question 25.
Are sound waves in air longitudinal or transverse?
Answer:
Longitudinal.
Question 26.
Can you notice the Doppler effect if both the listener and the source of sound are moving with the same velocity in the same
direction? Why?
Answer:
No. This is because there is no relative motion between the source of sound and the listener.
Question 27.
If oil of density higher than that of water is used in place of water in a resonance tube, how does the frequency change?
Answer:
The frequency is governed by the air column and does not depend, upon the nature of the liquid. So frequency would not change.
Question 28.
Which property of the medium enables the transverse waves to pass through it?
Answer:
Modulus of rigidity.
Question 29.
In a thunderstorm why flash of light is seen earlier than the sound of thunder?
Answer:
The speed of light is much higher than the speed of sound waves.
Question 30.
What is the main difference between the brazing of a honeybee and the roaring of a lion?
Answer:
Brazing of honeybee is of high pitch and lion’s roar has high intensity.
Question 31.
If you set your watch by the sound of a distant siren, will it go fast or slow?
Answer:
It will go slow due to the low value of the speed of sound in the air.
Question 32.
What is a dispersive medium?
Answer:
A medium in which the wave velocity depends on the frequency of the wave is called a dispersive medium.
Question 33.
Will sound be louder at node or antinode in a stationary wave?
Answer:
It will be louder at node due to large pressure variation there as
ΔP = – strain × elasticity.
Question 34.
Even if a powerful thermonuclear explosion takes place on a planet, the sound is not heard on Earth. Why?
Answer:
The interplanetary space is devoid of continuous material. In the absence of a material, the medium sound is not heard on the earth.
Question 35.
In older days messages were conveyed to distant villages by beating of big drums. Why?
Answer:
It has a larger area and the intensity of sound (I) is directly proportional to the area of an oscillator (A) i.e. I ∝ A.
Question 36.
Which is the most basic property of the wave?
Answer:
Frequency is the basic property of the wave.
Question 37.
You can make waves in a pond by throwing a stone in it. What is the source of energy of the wave?
Answer:
The kinetic energy of the stone is the source of wave energy.
Question 38.
Why echoes are not heard in a small room?
Answer:
Because the minimum distance between the obstacle reflecting sound waves and the source of sound is less than 17 m in a small room, so echoes are not heard.
Question 39.
Name two properties that are common to all types of mechanical waves?
Answer:
- They require a material medium for their propagation.
- The medium itself does not move with the wave.
Question 40.
In sound, beats are heard when two independent sources are sounded together. Is it possible in the case of sources of light?
Answer:
No. This is because the phase difference between two independent sources of light is random.
Question 41.
Mention a condition when Doppler’s effect in sound is not applicable.
Answer:
When the velocity of the source or listener exceeds the velocity of sound.
Question 42.
What will be the velocity of sound in a perfectly rigid rod and why?
Answer:
Infinite because the value of Young’s modulus of elasticity is infinite for a perfectly rigid rod.
Question 43.
Sound is simultaneously produced at one end of two strings of the same length, one of rubber and the other of steel. In which string will the sound reach the other end earlier and why?
Answer:
In the case of steel-string as \(\frac{Y}{d}\) ratio is larger for steel than rubber.
Question 44.
Two persons cannot talk on the moon just as they do on the earth. Why?
Answer:
Due to the absence of air on the moon.
Question 45.
Graphs between the pressure P and the speed v in a gas are shown below. Explain with the reason which one is correct?
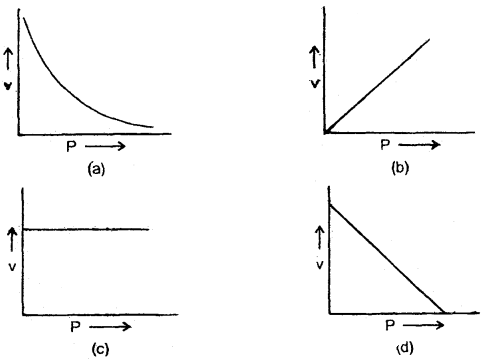
Answer:
(c) As the speed of sound (y) is independent of pressure, so y remains constant, hence (e) is correct.
Question 46.
Why the bells of colleges and temples are of large size?
Answer:
The larger the area of the source of sound more is the energy transmitted into the medium. Consequently, the intensity of sound is more and loud sound is heard.
Question 47.
State the limitations of Doppler’s effect.
Answer:
Doppler’s effect is applicable only when there is the relative velocity between the source and the listener and is less than the velocity of sound. The effect is not applicable if the relative velocity is greater than the velocity of sound i.e. if the source or observer moves with supersonic velocity.
Question 48.
Animals and human beings have two ears. What help do they render in listening sound from a distant source?
Answer:
The two ears receive sound in different phases, thus they help in locating the direction of the source of the sound. Turning of head and receiving sound in phase turns the direction.
Question 49.
An observer at a sea-coast observes waves reaching the coast. What type of waves does he observe? Why?
Answer:
Elliptical waves while the waves on the surface of the water are transverse, the waves just below the surface of the water are longitudinal. So the resultant waves are elliptical.
Question 50.
Why the reverberation time is larger for an empty hall than a crowded hall?
Answer:
It is due to the fact that the energy absorption in an empty hall is very small as compared to that of the crowded one.
Waves Important Extra Questions Short Answer Type
Question 1.
Here are the equations of three waves:
(a) y (x, t) = 2 sin (4x – 2t)
(b) y (x, t) = sin (3x – 4t)
(c) y (x, t) = 2 sin (3x – 3t).
Rank the waves according to their (A) wave speed and (B) maximum transverse speed, greatest first.
Answer:
(A) b, c, a.
Standard wave equation is y (x, t) = A sin (ωt – kx)
∴ (a) va = \(\frac{\omega}{k}=\frac{2}{4}=\frac{1}{2}\) unit = 0.5 unit.
(b) vb = \(\frac{\omega}{k}=\frac{4}{3}\)unit = 1.33 unit.
(C) Vc = \(\frac{\omega}{k}=\frac{3}{3}\) = 1 unit.
clearly vb > vc > va, so order is b, c, a.
(b) Transverse speed (vt) = \(\frac{\mathrm{d} y}{\mathrm{dt}}\)
∴ |(vt)a| = 2 × 2 = 4
|(vt)b| = 4
|(vt)c| = 2 × 3 = 6
∴ clearly (c), (a) and (b) tie.
Question 2.
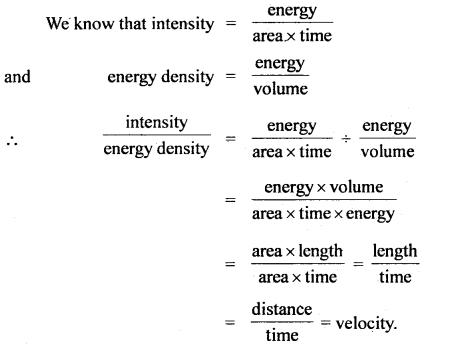
Which physical quantity is represented by the ratio of the intensity of wave and energy density? Why?
Answer:
Velocity.
Question 3.
When are the tones called harmonics?
Answer:
The tones are called harmonics if the frequencies of the fundamental tone and other overtones produced by a source of sound are in the harmonic series.
Question 4.
What will be the effect on the frequency of the sonometer wire if the load stretching the sonometer wire is immersed in water?
Answer:
Due to the upthrust due to buoyancy experienced by the load, the effective weight will decrease, so tension and hence frequency will decrease as v ∝ \(\sqrt{T}\).
Question 5.
An organ pipe is in resonance with a tuning fork. If the pressure of air in the pipe is increased by a factor of 139, then how should the length be changed for resonance?
Answer:
We know that the velocity of sound is independent of pressure, so there is no change in frequency and hence there is no need to change the length of the pipe.
Question 6.
Sound waves travel through longer distances during the night than during the day. Why?
Answer:
Earth’s atmosphere is warmer as compared to the surface of the earth at night. The temperature increases with altitude and thus the velocity of sound increases. It is a case of reflection from denser to rarer medium.
The sound waves get totally internally reflected.
Question 7.
Water is being continuously poured into a vessel. Can you estimate the height of the water level reached in the vessel simply by listening to the sound produced?
Answer:
Yes, the frequency of the sound produced by an air column is inversely proportional to the length of the air column. As the level of water in the vessel rises, the length of the air column in the vessel decreases, so the frequency of sound increases, and hence shrillness of sound increases.
From the shrillness of sound, we can have a rough estimate of the level of water in the vessel.
Question 8.
A sonometer wire resonates with a tuning fork. If the length of the wire between the bridges is made twice even then it can resonate with the same fork. Why?
Answer:
When the length of the wire is doubled, the fundamental frequency is halved and the wire vibrates in two segments so the sonometer wire will still resonate with the given tuning fork.
Question 9.
Doppler’s effect in sound is asymmetric. Explain.
Answer:
Sound waves require a material medium for their propagation.
The apparent frequency is different whether the source moves towards the stationary observer or an observer moves towards the stationary source. Thus the Doppler’s effect is said to be asymmetric. No such asymmetry occurs in light because apparent frequency remains the same in either the case whether the source or the listener moves.
Hence Doppler’s effect is said to be symmetric in light.
Question 10.
What is redshift?
Answer:
It is due to Doppler’s effect in the case of light waves. It is known that all stars are moving away from each other. So apparent frequency of light from a star as received by an observer on earth is less than the actual frequency. Since wavelength is inversely proportional to the frequency, the apparent wavelength of light from stars is more than the actual wavelength.
In other words, due to the Doppler effect, the wavelength of light shifts towards a longer end i.e. towards red color and so it is called redshift.
Question 11.
A sitar wife and a tabla when sounded together give 4 beats/ sec. What do we conclude from this? As the tabla membrane is tightened, the beat rate increases or decreases, explain.
Answer:
When sitar and tabla are sounded together, they give 4 seats/ sec. From this, we conclude that the frequencies of the two sounds differ by 4. If the frequency of tabla is greater than that of a sitar, then on tightening the tabla membrane, the frequency of tabla will further increase and hence the difference in frequencies will increase.
Thus beat rate will increase. If the frequency of tabla is less than that of sitar, then on tightening the tabla membrane, the frequency of tabla will increase and the difference in frequencies will decrease. So beat rate will decrease.
Question 12.
Explain why frequency is the most fundamental property of a wave.
Answer:
When a wave passes from one medium to another, its velocity and wavelength change but the frequency remains the same. Hence frequency is said to be the most fundamental property of a wave.
Question 13.
Sound is produced by vibratory motion, explain why then a vibrating pendulum does not produce sound?
Answer:
The sound which we can hear has a frequency from 20 Hz to 20,000 Hz.
The frequency of the vibrating pendulum does not lie within the audible range and hence it does not produce sound.
Question 14.
Explain why stringed instruments are provided with hollow boxes.
Answer:
The hollow boxes are set into forced vibrations along with the strings. The loudness is higher if the area of the vibrating body is more. So hollow boxes attached to increase the loudness of sound.
Question 15.
When we start filling an empty bucket with water, the pitch of sound produced goes on changing. Why?
Answer:
An empty bucket behaves as a closed organ pipe. The frequency of fundamental note produced by it is given by
v = \(\frac{v}{4l}\).
As the bucket starts filling, the length (l) of the resonating air column decreases, and hence frequency increases. Since the pitch of a sound depends upon the frequency. So it changes with the change in frequency.
Question 16.
Two loud-speakers have been installed in an open space to listen to a speech. When both are operational, a listener sitting at a .particular- place receives a very faint sound. Why? What will happen if one loud-speaker is kept off?
Answer:
When the distance between two loud-speakers from the position of listener is an odd multiple of \(\frac{λ}{2}\), then due to destructive interference between sound waves from two loud-speakers, a feeble sound is heard by the listener.
When one loud-speaker is kept off, no interference will take place and the listener will hear the full sound of the operating loud-speaker.
Question 17.
Why is the sound produced in the air not heard by a person deep inside the water?
Answer:
The velocity of sound in water is much lesser than the velocity of sound in air. So the sound waves are mostly reflected from the surface of the water. Only little refraction of sound from air to water takes place. Moreover, the refracted sound waves die off after traveling a small distance in the water. Hence no sound waves reach deep inside the water.
Question 18.
The reverberation time is larger for an empty hall than a crowded hall. Explain why?
Answer:
The sound prolongs for a longer time in an empty hall as it does not get absorbed. In the case of a crowded hall, the sound is absorbed by the audience. Hence reverberation time is less in the crowded hall.
Question 19.
If a balloon is filled with C02 gas, then how will it behave for sound as a lens? On filling it with hydrogen gas, what will happen?
Answer:
The speed of sound in CO2 is less than in air (∴ v ∝ \(\frac{1}{\sqrt{\rho}}\)). So the balloon filled with CO2 gas behaves as a concave lens.
When it is filled with hydrogen, the speed of sound in H2 gas becomes greater than in air. So it will behave as a convex lens.
Question 20.
Why on reflection from the rigid surface, the wave does not change type, and only phase change occurs, while on reflection from a smooth surface, type changes while phase does not change?
Answer:
When a compression strikes the rigid surface, the surface does not move but pushes the compression back as such. On the other hand, the direction of vibration of the particles of the medium is reversed. Thus the type of wave does not change while phase change occurs.
When a compression strikes the smooth surface (i.e. yielding surface), the compression continues to move forward with the surface. But due to refraction, a part of the wave moves backward. Thus type changes while phase does not change.
Question 21.
Explain why transverse elastic waves can’t propagate through a fluid?
Answer:
When a transverse elastic wave travels through a solid, a shearing strain develops which is supported by the elastic solid because of the development of a restoring force. Thus elastic waves can propagate through solids.
But a liquid or a gas (i.e. fluid) can’t support a shearing strain. So there will be no restoring forces when there are transverse displacements and so transverse vibrations are not possible.
Question 22.
Two strings of the same material and length under the same tension may vibrate with different fundamental frequencies. Why?
Answer:
The frequency of vibration of the string is given by
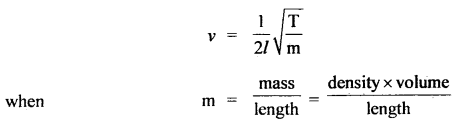
If ρ = density of the material of string.
l, r = its length and radius.
D = diameter = 2r, then
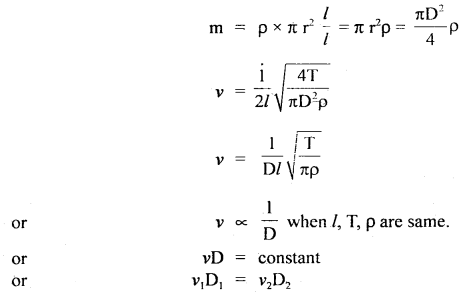
Hence the two strings may vibrate with different frequencies when they have different diameters.
Question 23.
Distinguish between transverse waves and longitudinal waves.
Answer:
Longitudinal waves:
- Particles of the medium vibrate along the direction of propagation of the wave.
- They travel in the form of alternate compressions and rare¬factions.
- They can be formed in any medium i.e. solid, liquid, or gas.
- When these waves propagate, there are pressure changes in ‘ the medium.
- They can’t be polarised.
Transverse waves:
- Particles of the medium vibrate, to the direction of propagation of the wave.
- They travel in the form of alternate crests and troughs.
- These can be formed in solids and on the surfaces of liquids only.
- There are no pressure changes due to the propagation of these waves in the medium.
- They can be polarised.
Question 24.
Distinguish between progressive waves and stationary waves.
Answer:
Progressive waves:
- The disturbance travels onward. It is1 handed over from one particle to the next.
- Energy is transported in the medium along with the propagation of waves.
- Each particle of the medium executes S.H.M. with the same amplitude.
- No particle of the medium is permanently at rest.
- Changes in pressure and density are the same at all points of the medium.
Stationary waves:
- The disturbance is confined to a particular region and there is no onward motion.
- No energy is transported in the medium.
- All the particles of the medium except at nodes execute S.H.M. with different amplitude.
- The particles of the medium at nodes are at rest.
- The changes of pressure and density are maximum at nodes and minimum at antinodes.
Question 25.
Distinguish between musical sound and noise.
Answer:
Musical sound:
- It produces a pleasant effect on the ear.
- It has a high frequency.
- There are no sudden changes in the amplitude of the musical sound waves.
- It is a desirable sound.
Noise:
- It produces an unpleasant effect on the ear.
- It has a low frequency.
- There are sudden changes in the amplitude of noise waves.
- It is an undesirable sound.
Question 26.
What are the characteristics of wave motion?
Answer:
- Wave motion is a form of disturbance that travels in a medium due to repeated periodic motion of the particles of the medium.
- The wave velocity is different from the particle velocity.
- The vibrating particles of the medium possess both K.E. and P.E.
- The particle velocity is different at different positions of its vibrations whereas wave velocity is constant throughout a given medium.
- Waves can undergo reflection, refraction, diffraction, dispersion, and interference.
Question 27.
Show that for 1°C change in temperature, the velocity of sound changes by 0.61 ms-1.
Answer:
We know that v ∝ \(\sqrt{T}\) .
If vt and vo be the velocity of sound at T°C and 0°C respectively,
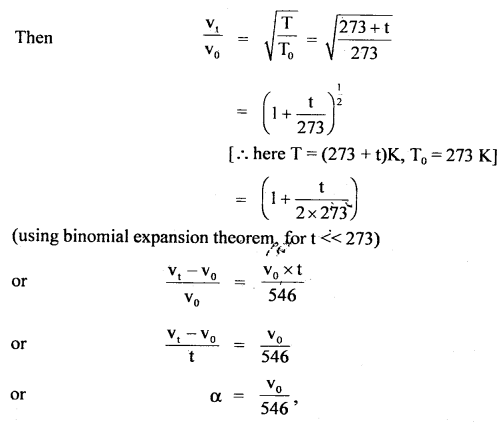
where α = \(\frac{\mathbf{v}_{\mathrm{t}}-\mathbf{v}_{0}}{\mathrm{t}}\) is called temp. coefficient of the velocity of sound.
Putting vo = 332 ms-1 at T0 i.e. 0°C, we get
α = \(\frac{332}{546}\) = 0.61 ms-1 °C-1
Question 28.
An electric bell is put in an evacuated room (a) near the center (b) close to the glass window, in which case the sound is heard (i) inside the room, (ii) out of the room.
Answer:
- Sound is not heard in cases (a) and (b) inside the room as the medium is not there for the propagation of sound.
- In case (a) sound cannot be heard outside for the reason given in (i) above.
In case (b) since the bell is very close to the window, the glass pane picks up its vibrations which are conveyed to the eardrum through the air outside the room. So, the sound can be heard in condition (b).
Question 29.
One of the primitive musical instrument is flute, yet produces good musical sound, how?
Answer:
The flute is an open organ pipe instrument having some holes which determine the wavelength and hence the frequency of sound. produced. By closing one or more holes, the length of the vibrating air column is changed and thus different harmonics are produced. The harmonic rich sound is a good musical sound.
Question 30.
Write basic conditions for the formation of stationary waves.
Answer:
The basic conditions for the formation of stationary waves are listed below:
- The direct and reflected waves must be traveling along the same line.
- For stationary wave formation, the superposing waves should either be longitudinal or transverse. A longitudinal and a transverse wave cannot superpose.
- For the formation of stationary waves, there should not be any relative motion between the medium and oppositely traveling waves.
- The amplitude and period of the superposing waves should be the same.
Question 31.
What is the difference between interference and stationary waves? In which phenomenon, out of the two, energy is not propagated? Why there is no energy at interference minimum?
Answer:
The superposition of two waves close to each other traveling in the same direction produces interference. The energy gets redistributed. It is minimum or zero at points of destructive interference and maximum at points of constructive interference. It is to be noted that the interference minima may not be points of zero energy unless •, the frequencies and amplitudes of the superposing waves are exactly equal.
The superposition of two similar waves (waves having the same amplitude and period) traveling in opposite direction produce stationary waves The nodes have no vibration of particles but antinodes have a maximum amplitude of vibration.
Question 32.
Write the applications of beats.
Answer:
Beats are used to:
- Determine an unknown frequency by listening to the best frequency Δv. Then unknown frequency V’ = v ± Δv where v is known and it is close to the unknown frequency. The exact value of v’ is found by loading and filling the tuning fork of unknown frequency from which + or – sign is chosen.
- Tune musical instruments by sounding them together and reducing beats number to zero.
- Make a sound rich in musical effect by the deliberate introduction of beats between different musical instruments.
- To produce very low-frequency pulses which otherwise cannot be produced. The beat frequency is the low-frequency sound.
- Receive radio program by the superheterodyne method.
- Detect harmful gases in mines.
Waves Important Extra Questions Long Answer Type
Question 1.
Derive expressions for apparent frequency when
(i) source is moving towards an observer at rest.
(ii) the observer is moving towards the source at rest.
(iii) both source and observer are in motion.
Answer:
Let S and O be the positions of. source and observer respectively.
υ = frequency of sound waves emitted by the source.
v = velocity of sound waves.
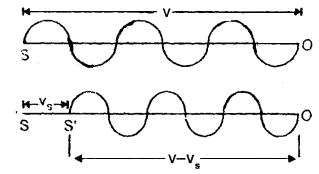
Case (i) Source (S) in motion and observer at rest: When S is at rest, it will emit waves in one second and these will occupy a space of length v in one second.
If λ = wavelength of these waves, then
λ = \(\frac{v}{υ}\) …(i)
Let vs = velocity of a source moving towards O at rest and let S reaches to S’ in one second. Thus the sound waves will be crowded in length (v – vs). So if λ’ be the new wavelength,
Then λ’ = \(\frac{v-v_{s}}{v}\)
if υ’ be the apparent frequency, then
υ’ = \(\frac{v}{\lambda^{\prime}}=\frac{v}{v-v_{s}}\)υ
∴ υ’ > v i.e. when S moves towards O, the apparent frequency of sound waves is greater than the actual frequency.
(ii) If the observer moves towards the source at rest:
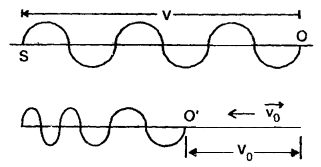
Let vo = velocity of an observer moving towards S at rest.
As the observer moves towards S at rest, so the velocity of sound waves w.r.t. the observer is v + vo.
If υ’ = apparent frequency, then
υ’ = \(\frac{\mathbf{v}+\mathbf{v}_{0}}{\lambda}=\frac{\mathbf{v}+\mathbf{v}_{0}}{\mathbf{v}}\)υ
clearly v’ > υ.
(iii) If both S and O are moving
(a) towards each other: We know that when S moves towards stationary observer,
![]()
then υ’ = \(\frac{\mathbf{v}}{\mathbf{v}-\mathbf{v}_{\mathrm{s}}}\)
When O moves towards S, then
υ” = \(\left(\frac{v+v_{0}}{v}\right) v^{\prime}=\left(\frac{v+v_{0}}{v-v_{s}}\right) v\)
(b) If both S and O move in the direction of sound waves:
Then the apparent frequency is given by
![]()
υ” = \(\left(\frac{\mathbf{v}-\mathbf{v}_{0}}{\mathbf{v}-\mathbf{v}_{\mathrm{s}}}\right)\)υ
(c) When both S and O are moving away from each other:
When source moves away from O at rest, then apparent frequency is given by
υ’ = \(\frac{v}{v+v_{s}}\)υ

When the observer is also moving away from the source, the frequency v’ will change to v” and is given by
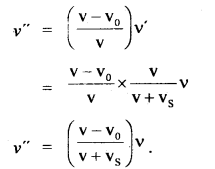
Question 2.
Give the analytical treatment of beats.
Answer:
Consider two simple harmonic progressive waves traveling simultaneously in the same direction and in the same medium. Let
- A be the amplitude of each wave.
- There is no initial phase difference between them.
- Let v1 and v2 be their frequencies.
If y1 and y2 be displacements of the two waves, then
y1 = A sin 2π v1 t and
y2 = A sin 2π v2 t
If y be the result and displacement at any instant, then
y = y1 + y2
= A (sin 2π v1 t) + sin (2π v2 t)
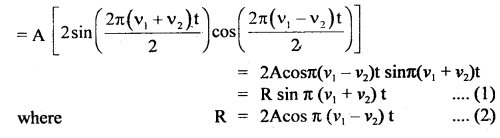
is the amplitude of the resultant displacement and depends upon t. The following cases arise.
(a) If R is maximum, then
cos π (v1 – v2) t = max. = ±1 = cos nπ
∴ π (v1 – v2) t = nπ
or
t = \(\frac{\mathrm{n}}{v_{1}-v_{2}}\) …(3)
where n = 0, 1, 2, …..
∴ Amplitude becomes maximum at times given by
t = \(0, \frac{1}{v_{1}-v_{2}}, \frac{2}{v_{1}-v_{2}}, \frac{3}{v_{1}-v_{2}}\)…..
∴ Time interval between two consecutive maxima is
= \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v1 – v2
∴ no. of beasts formed per sec. = v1 – v2.
(b) If R is minimum, then
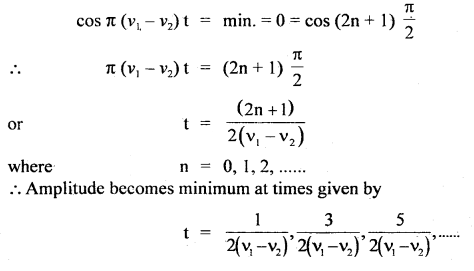
∴ Time interval between two consecutive minima is = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v1 – v2
∴ no. of beasts formed per sec. = v1 – v2.
Hence the number of beats formed per second is equal to the difference between the frequencies of two component waves.
Question 3.
What conditions are necessary for the good acoustical properties of the building? How are they met?
Answer:
An acoustically good building is one in which the sound is heard clearly in every nook and corner, some conditions must be fulfilled.
These are:
(a) the building should have proper reverberation time, the reverberation time is given by Sabine’s formula which for a hall is
T = \(\frac{0.166 \mathrm{~V}}{\sum \alpha \mathrm{A}}\)
The reverberation time is adjusted by:
- changing the volume (V): This can be changed little due to the size of the hall already fixed.
- changing effective absorbing area: This can be done artificially by putting heavy curtains, paintings, providing open windows, wall coverings, etc.
- providing sufficiently energetic sound: The sound should be sufficiently loud and intelligible at every point.
- eliminating echo: Except for the desired one, echoes must be eliminated.
- properly focussing the sound: The sound has to be properly focussed to avoid the source of silence and also unreliable focussing.
- avoiding unique reinforcement: No single overtone should uniquely be reinforced then the total quality of the note will be affected.
- avoiding extra noise: Extra noises including resonance within the building has to be avoided.
- eliminating smooth curved surfaces: Smooth surfaces reflect sound sharply which may cause several problems.
To achieve these goals following steps need to be taken:
(a) Properly design the building to optimize its acoustic condition.
(b) Decorate selectively the building with paintings, floral designs, perforations.
(c) Use false perforated or cardboard ceilings, and perforated structures at the curved walls.
(d) Use carpets, upholster seats with holes in the bottom.
(e) Use carpets or mats etc. on floors.
(f) Heavy curtains, wall hangings, etc. should be used.
(g) Properly place the mike and loud-speakers in the hall.
(h) Avoid sharp corners in the hall and make the stage back parabolic with mike at its focus.
Numerical Problems:
Question 1.
How far does the sound travel in the air when a tuning fork of frequency 280 Hz makes 15 vibrations? Given the velocity of sound is 336 ms-1.
Answer:
Velocity of sound, v = 336 ms-1
frequency, v = 280 Hz
∴ Time of one complete vibration,
T = \(\frac{1}{v}=\frac{1}{280}\) s.
Time to complete 15 vibrations,
t = 15 T
= \(\frac{1}{280}\) × 15
If x be the distance covered in time t, then
x = v × t
= 336 × \(\frac{15}{280}\) = 18 m
x = 18 m.
Question 2.
Audible frequencies have a range of 20 Hz to 20 × 103 Hz.
Express this range in terms of
(i) period T,
(ii) wavelength λ,
(iii) angular frequency CD.
Given the velocity of sound = 340 ms-1.
Answer:
V = 340 ms-1
Using v1 = 20 Hz
v2 = 20 × 103 Hz
(i) T = \(\frac{1}{v}\), we get
T1 = \(\frac{1}{20}\) = 0.005 s
and T2 = \(\frac{1}{20}\) × 103
= 0.00005 s = 5 × 10-5 s.
(ii) we know that
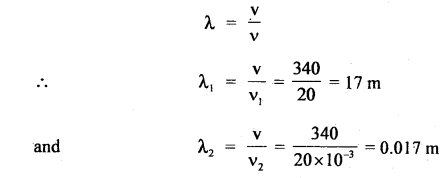
∴ The wavelength range is 17 m to 0.0 17 m.
(iii) Angular frequency, ω = 2πv
∴ ω1 = 2πv1 = 2π × 20= 40π rads-1
ω2 = 2πv2 = 2π × 20 × 103
= 40π × 103 rad s-1
∴ angular frequency range is 40π rad s-1 to 40π × 103 rad s-1
Question 3.
A copper wire is held at the two ends by rigid supports. At 30°C, the wire is just taut with negligible tension. Find the speed of transverse waves in the wire at 10°C. α = 1.7 × 10-5 °C-1, λ = 1.4 × 1011 Nm-1 and ρ = 9 × 103 kg m-3
Answer:
When the temperature changes from 30°C to 10°C, then the change in length of the wire is
Δl = l ∝ Δt = l × 1.7 × 10-5 × 20
= 3.4 × l × 10-4 m
Here, ρ = 9 × 103 kg m-3
Y = 1.4 × 1011 Nm-2
Δt = 30 – 10 = 20°C
α = 1.7 × 10-5 °C-1
Now Y = \(\frac{\mathrm{F} / \mathrm{a}}{\mathrm{\Delta}l / \mathrm{l}}\)
or
F = Ya \(\frac{Δl}{l}\)
where a = area of cross section of the wire.
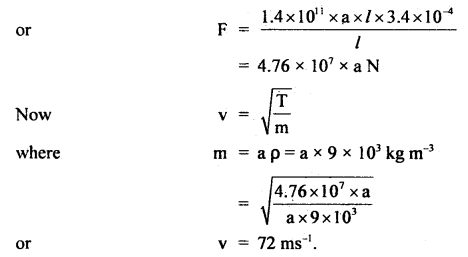
Question 4.
The speed of sound in hydrogen is 1270 ms-1. What will be the speed in a mixture of oxygen and hydrogen mixed in a volume ratio of 1:4?
Answer:
Let V1 and V2 be the volumes of O2 and H2 respectively in the mixture.
ρ1 and ρ2 be their respective densities.
If m1 and m2 be the mass of oxygen and hydrogen respectively, then
m1 = V1ρ1
and m2 = V2ρ2
If ρ be the density of the mixture, then
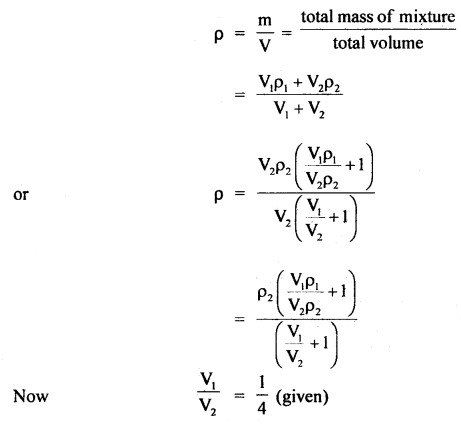
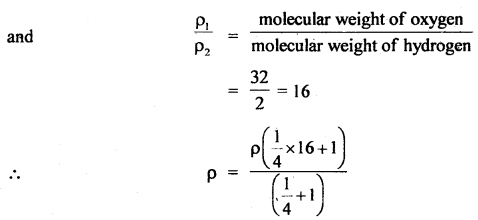
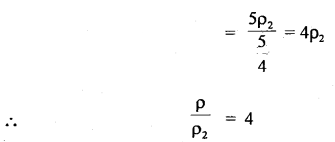
Also, let v1 = velocity of sound in the mixture
and v2 = velocity of sound in the hydrogen
= 1270 ms-1.

Question 5.
A tuning fork A of unknown frequency is sounded with a tuning fork B of frequency 288. Four beats are heard in one second. Tuning fork A is then loaded with a little wax and again sounded with fork B. Again 4 beats are heard in one second. What is the frequency of A?
Answer:
Since tuning fork A of known frequency say v gives 4 beats/ sec with B of frequency 288, so frequency of tuning fork A is given by
∴ v = 288 ± 4 = 284 or 292.
On loading A with wax, it again produces 4 beats/s with B of frequency 288.
If the frequency of A is 292, it means on loading A with wax, its frequency falls to 284 which can produce 4 beats/s with a B frequency of 288. So the frequency of A maybe 292.
If the frequency of A is 284, on loading it with wax, its frequency falls below 284 so that when it is sounded with B of frequency 288, it forms more than 4 beats/s which is not consistent with the given condition.
So the frequency of A can’t be 284. Hence the frequency of A = 292.
Question 6.
The first overtone of an open organ pipe beats with the first overtone of a closed organ pipe with a beat frequency of 2.2 Hz. The fundamental frequency of a closed organ pipe is 110 Hz. Find the lengths of the pipes. The velocity of sound in air = 330 ms-1.
Answer:
Fundamental frequency of closed organ pipe is
vc = \(\frac{\mathrm{v}}{4 \mathrm{~L}_{\mathrm{c}}}\)
Lc = length of closed pipe v
or
Lc = \(\frac{\mathrm{v}}{4 \mathrm{~v}_{\mathrm{c}}}\)
Here, νc = 110 Hz
v = 330 ms-1
∴ Lc = \(\frac{330}{4 \times 110}\) = 0.75m = 75 cm. 0.4 × 110
Now frequency of first overtone of open pipe is
v1 = \(\frac{\mathrm{v}}{\mathrm{L}_{0}}\)
where Lo = length of open pipe Frequency of first overtone of closed pipe is
Frequency of first overtone of closed pipe is
ν2 = \(\frac{3 v}{4 L_{c}}=3\left(\frac{v}{4 L_{c}}\right)\)
= 3νc = 3 × 110 = 330 Hz
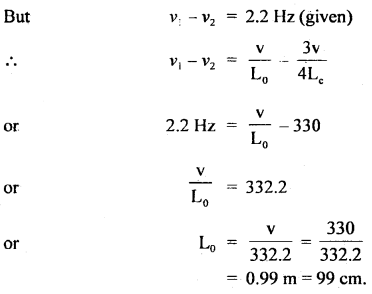
Question 7.
An open pipe is suddenly closed at one end with the result that the frequency of the 3rd harmonic of the closed pipe is found to be higher by loo Hz than the fundamental frequency of the open pipe. What is the fundamental frequency of open pipe?
Answer:
νo = \(\frac{v}{2L}\)
where ν0 = fundamental frequency of open pipe. The frequency of the third harmonic of closed pipe is
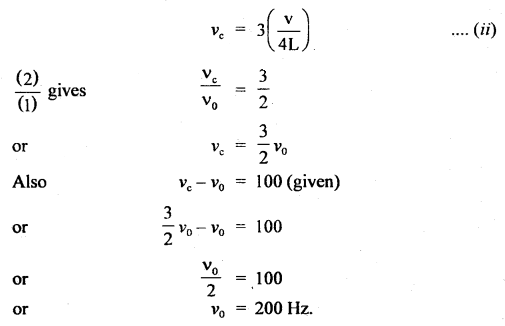
Question 8.
A set of 24 tuning forks is so arranged that each gives 4 beats per second with the previous one and the last sounds the octave of the first. Find the frequency of the first and last.
Answer:
As the last is the octave (double) of the first, so the frequencies are ¡n the increasing order.
Let frequency of the first = x
frequencyofthe2nd = x + 4
frequency olthe3rd = x + 2(4)
frequency of the 24th = x + 23 (4)
But this is the octave of the first
∴ frequency of the 24th = 2(x) (given)
∴ x + 23(4) = 2x
or
x = 92
∴ frequency of last tuning fork 2 × 92 = 184 Hz.
Question 9.
A drop of water 2 mm in diameter falling from a height of 50 cm in a bucket generates a sound that can be heard from a 5 m distance. Take all gravitational energy difference equal to sound energy, the transformation being spread in time over 0.2s, deduce the average intensity. Take g = 10 ms2.
Answer:
Here, ρ of water = 103 kg m-3
D = 2mm
∴ radius = r = \(\frac{2}{2}\) = 1 mm = 10-3 m
h = 50cm = 0.50 m
g = 10 ms-2
d = 5m
∴ a = area in which sound is heard
=4πd2
I = intensity of sound =?
Now I = \(\frac{\text { energy transference }}{\text { time } \times \text { area }}\)
= \(\frac{\text { P.E. of drop }}{\text { time } \times \text { area }}=\frac{m g h}{t \times a}\) …(1)
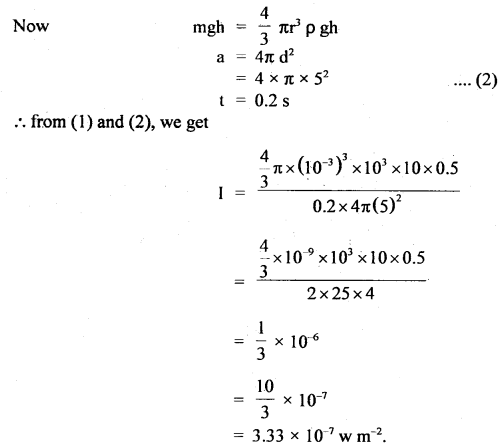
Question 10.
A train moves towards a stationary observer with a velocity of \(\frac{1}{30}\)th of the velocity of sound. The whistle of the engine regularly blows after one second. What ¡s the interval between successive sounds of the whistle as heard by the observer?
Answer:
Actual time interval between successive blows of whistle = 1 sec.
∴ Actual frequency of whistle, v = 1 Hz
Let v = velocity of sound
∴ velocity of source, vs = \(\frac{v}{30}\)
∴ apparent frequency of the whistle is
ν’ = \(\frac{v}{v-v_{s}}\) × ν = \(\frac{v}{v-\frac{v}{30}}\) × 1
or
ν’ = \(\frac{30}{29}\) Hz
∴ Apparent time interval between two successive sounds of whistle is
t = \(\frac{1}{v^{\prime}}=\frac{29}{30}\) s.
Question 11.
The splash is heard 4.2,3 s after a stone is dropped into a well which is 78.4 m deep. Find the velocity of sound in the air.
Answer:
Here, Depth of well, h = 78.4 m
v = velocity of sound = ?
t = total time after which splash is heard = 4.23 s.
t1 = time taken by stone to hit water surface in the well.
t2 = time the sound takes in reaching top of the well.
∴ t1 +t2 = 4.23 s
u = 0, g = 9.8 ms-2, h = 78.4m, t = t1
using the relation, s = ut + \(\frac{1}{2}\) at2, we get
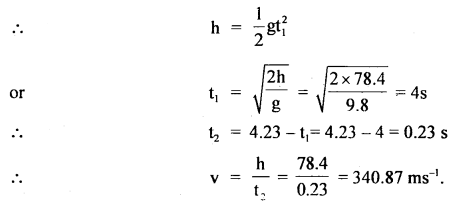
Question 12.
What is the intensity level in dB of sound whose intensity is 10-6 watt m-2. Take zero levels of intensity = 10-2 watt m-2.
Answer:
Here,
I = 10-6 w m-2
I0 = 10-12 w m-2
L =?
L = log10 \(\left(\frac{I}{I_{0}}\right)\) = log10 \(\left(\frac{10^{-6}}{10^{-12}}\right)\)
= log10 106
= 6 log10 10 = 6 × 1 = 6B
As 1B = 10 dB
∴ L = 6 × 10 = 60 dB
Question 13.
Two closed organ pipes when sounded together produce 12 beats in 4s at a temperature of 27°C. Find the temperature at which the number of beats produced is 16 during the same period.
Answer:
Let v1 and v2 be the frequencies produced by the two organ pipes at 27°C. Let v27 be the velocity of sound at 27°C.
and vt = velocity of sound at t°C
l1, l2 be their lengths respectively.
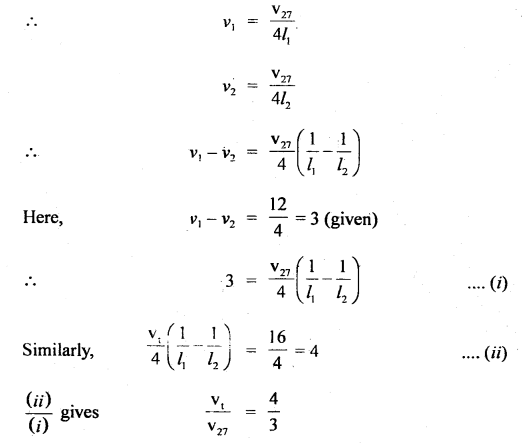

Question 14.
A police-man on duty detects a drop of 15% in the pitch of the horn of a motor car as it crosses him. If the velocity of sound is 330 ms-1, calculate the speed of a car.
Answer:
vs = speed of car = ?
v = velocity of sound = 330 ms-1
v = frequency of sound emitted by horn
If v’ be the apparent frequency’of sound when car approaches the police man, then
ν’ = \(\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_{\mathrm{s}}}\) × ν …(i)
Also let ν” be the apparent frequency of sound when car recedes away from the police man, then
ν” = \(\frac{\mathrm{v}}{\mathrm{v}+\mathrm{v}_{\mathrm{s}}}\) × ν …(ii)

Question 15.
A wire of length 80 cm has a frequency of 250 Hz. If the length of the wire is increased to 100 cm and tension is reduced to \(\frac{1}{4}\)th of its original value, then calculate the new frequency.
Answer:
l1 = initial length = 80 cm
ν1 = 250 Hz
Let T1 = T be the tension
l2 = 100 cm
T2 = \(\frac{1}{4}\)T1 = \(\frac{T}{4}\).
ν = ?
Using the relation
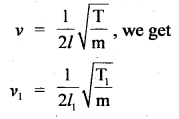
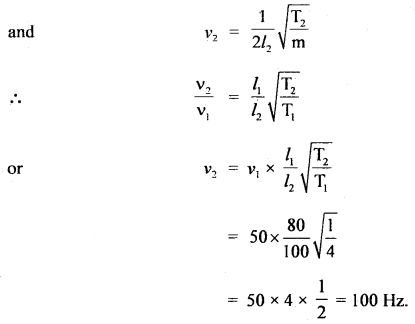
Question 16.
A tuning fork A of unknown frequency is sounded with a tuning fork B of frequency 512 Hz. 8 beats are heard in 1 second. Tuning fork A is then loaded with a little wax and sounded together with B. Again 8 beats are heard in 1 second. Find the frequency of
Answer:
Let ν = frequency of tuning fork A
No. of beats formed/sec. =8
∴ ν = 512 ± 8 = 520, 504
On loading A with wax, it again produces 8 beats/second with B of frequency 512.
Now if νA = 520, then it means its frequency decreases on loading. If v. falls to 504 then it will produce 8 beats/sec. with B.
∴ νA = 520
If νA is 504, then on loading its frequency falls below 504, so it forms more than 8 beats/sec. when sounded together with B which is not consistent with the given condition.
So the frequency of A cannot be 504.
∴ νA = 520 Hz.
Question 17.
Two engines pass each other in opposite directions with a velocity of 60 km ph. One of them is emitting a note of frequency 540 Hz. Calculate the frequencies heard in the other engine before and after they have passed each other. The velocity of sound = 316.67 ms-1.
Answer:
Here, vs = vo = 60 kmph = 60 × \(\frac{5}{18}\) = 16.67 ms-1
ν = 540 Hz
ν’ = ?
v = velocity of sound = 316.67 ms-1
Case A: Before passing each other:
v = 316.67 ms-1
vs = vo = 16.67 ms-1
∴ ν’ = ?
Using the relation
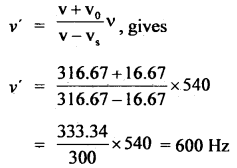
Case B: After passing each other:
vs = – 16.67 ms-1
vo = – 16.67 ms-1
v = 316.67 ms-1
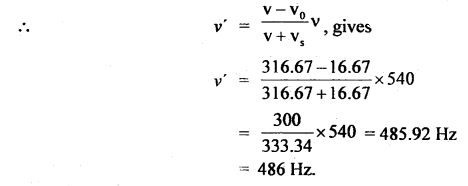
Question 18.
The audible frequency range of a human ear is 20 Hz to 20 kHz. Convert this into the corresponding wavelength range. Take the speed of sound in the air to be 340 ms-1.
Answer:
Here, ν1 = 20 Hz
ν2 = 20000 Hz
v = 340 ms-1
λ1 = ?
λ2 = ?
∴ λ1 = \(\frac{v}{v_{1}}=\frac{340}{20}\) = 17 m
and λ2 = \(\frac{v}{v_{2}}=\frac{340}{20000}\) = 0.017 m
∴ Corresponding wavelength range is 0.017 to 17 m.
Question 19.
For aluminum, the bulk modulus and the modulus of rigidity are 7.5 × 1010 Nm-2 and 2.1 × 1010 Nm-2. Find the velocity of longitudinal and transverse waves in the medium. The density of aluminum is 2.7 × 103 kg m-3.
Answer:
Here, for aluminium, ρ = 2.7 × 103 kg m-3 .
η = 2.1 × 1010 Nm-2
k = 7.5 × 1010 Nm-2
vl = velocity of longitudinal waves = ?
vt = velocity of transverse waves = ?
Using the relation,
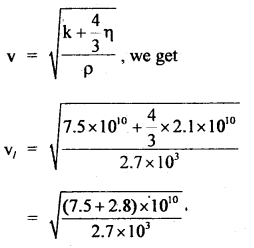
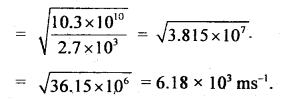
Also using the relation, for transverse waves,
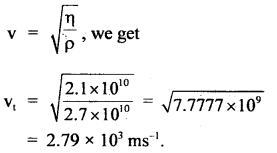
Question 20.
The velocity of sound at 27°C is 350 ms-1. If the density of air at N.T.P. is 1.293 kg m-3, calculate the ratio of the specific heats of air.
Answer:
Here, T = 27 + 273 = 300k
v27 =. velocity of sound at 27°C
= 350 ms-1
ρ = 1.293 kg m-3
To = 273 k
vo = velocity at N.T.P. = ?
P = 76 cm of Hg
= 0.76 × 13600 × 9.8 Nm-2
Using the relation,
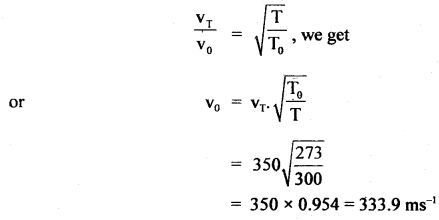
Using the relation,
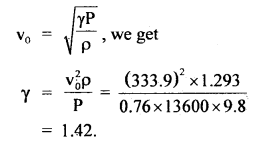
Question 21.
A tuning fork B produces 6 beats per second with another tuning fork of frequency 288 Hz. The tuning fork of unknown frequency is filed and the number of beats now produced is 4 per second. Calculate the frequency of the tuning fork.
Answer:
Known frequency of the fork =288 Hz
No. of beats/second = 6
∴ Unknown frequency = 288 ± 6 = 294 or 282.
When the prongs of tuning fork B are filed, its frequency increases. If the frequency of B is originally 294 Hz, on filing it will increase. So the difference between the frequencies will increase and hence no. of beats will also increase.
If the frequency of B is originally 282 Hz, then on filing it, its frequency will increase, so the difference between the frequencies will decrease, and hence the no. of beats will decrease.
In this case, when the prongs of B are filed, the no. of beats decreases from 6 to 4. Thus the frequency of the given tuning fork is 282 Hz.
Question 22.
Find the change in the frequency observed by a listener when a source approaching him with a velocity of 54 km h-1 starts going away from him with the same velocity. Take velocity of sound = 330 ms-1 and v = 300 Hz.
Answer:
Here, vs = 54 km h-1 = 54 × \(\frac{5}{18}\) = 15 ms-1
v = 330 ms-1
ν = 300 Hz
Case I: When the source is approaching, then
ν’1 = \(\frac{\mathbf{v}}{\mathbf{v}-\mathbf{v}_{\mathbf{s}}}\)ν = \(\frac{330}{330-15}\) × 300
= 314 Hz
Case II: When the source reduces then
ν’2 = \(\frac{\mathbf{v}}{\mathbf{v}+\mathbf{v}_{\mathbf{s}}}\)ν = \(\frac{330}{330+15}\) × 300
= \(\frac{330}{345}\) × 300
= 287 Hz
∴ Change in frequency,
ν’1 – ν’2 = 314 – 287 = 27 Hz.
Question 23.
A progressive wave is given by
y = 12 sin (5t – 4x)
On this wave, how far away are the two points having a phase difference of \(\frac{π}{2}\)?
Answer:
Here, ΔΦ = phase difference = \(\frac{π}{2}\)
Let Δx be the corresponding path difference,
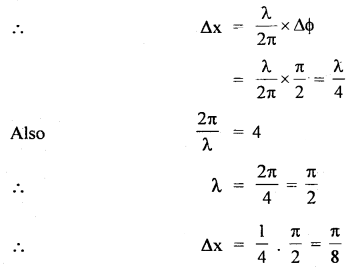
Question 24.
The figure here shows the wave, y = A sin (ωt – kx) at any instant traveling in the +x direction. What is the slope of the curve at B?
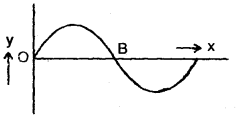
Answer:
Here, the particle velocity is maximum at B and is given by
vo = ωA.
Also, wave velocity is given by
C = \(\frac{ω}{k}\)
∴ So the slope \(\frac{v_{0}}{C}=\frac{\omega A}{\omega / k}\) = kA
Question 25.
Two sound waves
y1 = A1 sin 1000 π(t – \(\frac{x}{220}\) )
and y2 = A2 sin 1010 π(t – \(\frac{x}{220}\) ) are superposed. What is the frequency with which the amplitude varies?
Answer:
Rate of variation of amplitude is equal to the beat frequency.
Here, 2πν1 = 1000 π
or
ν1 = 500
and 2πν2 = 1010 π
or
ν2 = 505
∴ beat frequency = ν2 – ν1
= 505 – 500
= 5.
Value-Based Type:
Question 1.
A group of students went to a place on an excursion. While boating on seawater, the students identified a submerged Torpedo-shaped structure. The boys debated among themselves on what they saw. A student by the name of Sharath considering it as a threat informed the police. The police took necessary steps to protect the country from the enemy submarine. Sharath was rewarded.
(a) What can you say about the qualities exhibited by Sharath?
Answer:
Navigator is a responsible citizen, he is duty-minded, having a presence of mind.
(b) A SONAR system fixed in a submarine operates at a frequency of 40 kHz. An enemy submarine moves towards the
SONAR with a speed of 360 km/hr. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to bel450 m/s.
Answer:
Here, frequency of SONAR (Source) = 40 k Hz
= 4 × 103 Hz
Speed of the sound wave, V = 1450 m/s
Speed of the observer, Vo = 360 kM/h = 100 m/s
∴ Apparent frequency received by an enemy submarine ;
V’ = \(\left(\frac{V+V_{0}}{V}\right) \cdot V=\left(\frac{1450+100}{1450}\right)\) × 40 × 103
=4.276 × 104 Hz.
This frequency is reflected by the enemy submarine (Source) and observed by SONAR (Now observer).
In this case, Apparent frequency is given by
V” = \(\left(\frac{V}{V-V_{s}}\right) \times V^{\prime}=\left(\frac{1450}{1450-100}\right)\) × 4.276 × 104
=45.9k Hz
Question 2.
Jagat and Ram are working in the same company. Jagat has noticed that Ram is suffering from Cancer. Ram is not aware of this. When Jagat asks him to go for a checkup, Ram refused. He gets convinced how even when he realizes normal, it is very important to get the checkup done once a year.
(a) What according to you, are the values displayed by Jagat in helping Ram.
Answer:
He has concern for hi^ friend, also he has the knowledge of medical facilities available
(b) A hospital uses an ultrasonic scanner to locate tumors in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km/s? The operating fre¬quency of the scanner is 4.2 MHz.
Answer:
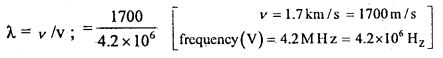
that is λ = 4.05 × 10-4 m
Question 3.
‘Preeti a student of class XI was reading the newspaper, The Headlines in the Newspaper were about the earthquake that had taken place in Assam on the previous day. She was very depressed seeing the loss of life and property. She approached her physics teacher and got the information about how an earthquake occurs.
(a) What can you say about the inquisitiveness of Preeti?
Answer:
She has concern for society and is sympathetic towards others.
(b) Earthquake generates sound waves inside the earth. Unlike a gas, the earth can experience both transverse (S) and longitudinal (P) sound waves. Typically the speed of the S wave is about 4 km/s, and that of the P wave is 8 km/s. A seismograph records P and S waves from an earthquake. The first P wave arrives 4 min before the first S wave. Assuming the waves travel in a straight line, how far away does the earthquake occur?
Answer:
LetV1 and V2 be the velocities of S waves and P waves and t1 , t2 be the time taken by these waves to travel to the position of seismograph. If l is the distance of occurrence of earthquake from the seismograph, .
∴ l = V1 t1 = V2t2
⇒ 4t1 = 8 t2
or
t1 = 2 t2 [∴ V1 = 4 kmh-1 ,V2 = 8 kmh-1]
Also, t1 – t2 = 4 min = 240 S.
2t2 – t2 = 240 [Using (i)]
or
t2 = 240 S and t1 = 2 × 240 = 480 S.
l = v1 t1 = 4 × 480 = 1920 km
Question 4.
Rajesh was waiting for the train on the platform with his parents. They were going to Mumbai and the train arrived half an hour late. He felt that when the train was coining towards the station, the intensity of the sound of the whistle was gradually increasing and on the platform the sound was maximum and when the train passes away the intensity of the whistle was decreasing.
Rajesh got confused and asked his father the reason behind it. His father could not give the correct answer. So, he decided to ask his physics teacher.
(i) What are the values displayed here by Rajesh?
Answer:
Values displayed by Rajesh are:
Awareness, curiosity, creativity, and intelligence,
(ii) Write the answer given by your teacher.
Answer:
The teacher explained that it is due to “Doppler’s effect”. Whenever there is a relative motion between the source and observer O. There is a change in observed frequency. So, the apparent frequencies of sound heard by the listener are different from the actual frequency of the sound of the source, which is given by.
V = Vo\(\left(\frac{V+V_{0}}{V+V_{s}}\right)\)
Here, V is the speed of sound through the j medium, Vo is the velocity of the observer relative to the medium, and Vs is the source velocity relative to the medium.