CBSE Sample Papers for Class 12 Physics Set 5 with Solutions

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Set 5 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Set 5 with Solutions

Time : 3 Hours
Maximum Marks: 70

General Instructions :

1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections: Section A, Section B, Section C. Section D and Section E.
3. Air the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion-Reasoning based questions of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study-based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants wherever necessary
   (i) c = 3 ×10⁸ m/s
   (ii) m_e = 9.1 × 10^-31 kg
   (iii) e = 1.6 × 10^-19 C 
   (iv) μ₀= 4π × 10^-17 TmA^-1
   (v) h = 6.63 × 10^-34 Js  
   (vi) ε₀ = 8.854 ×10^-12 C²N^-1m^-2
   (vii) Avogadro’s number = 6.023 × 10²³ per gram mole

Section – A

The following questions are multiple-choice questions with one correct answer. Each question carries 1 mark. There is no internal choice in this section.

Question 1.
An iron cored coil is connected in series with an electric bulb with an AC source as shown in figure. When iron piece is taken out of the coil, the brightness of the bulb will:

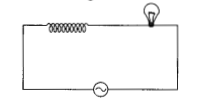
(a) decrease
(b) increase
(c) remain unaffected
(d) fluctuate
Answer:
(b) increase

Explanation:

As the iron rod is removed from the coil, the coil’s self-inductance falls, the circuit’s impedance drops, and the current rises as a result. Therefore, the electricity used by the bulb grows, as does the brightness of the bulb.
Hence option (b) is correct.

Question 2.
Which of the following statement is NOT true about the properties of electromagnetic waves?
(a) These waves do not require any material medium for their propagation.
(b) Both electric and magnetic field vectors attain the maxima and minima at the same time.
(c) The energy in electromagnetic wave is divided equally between electric and magnetic fields.
(d) Both electric and magnetic field vectors are parallel to each other.
Answer:
(d) Both electric and magnetic field vectors are parallel to each other.

Explanation: In electromagnetic waves,
1. The electric field and magnetic field vary continuously with time and have maxima and minima at the same place and at the same time.
2. Both electric and magnetic fields have the same energy.
3. Both electric and magnetic fields are perpendicular to each other and perpendicular to direction of propagation.
4. These waves don’t require any material medium to propagate, they can propagate in vacuum as well.
Hence option (d) is correct.

Question 3.
A rectangular, a square, a circular and an elliptical loop, all in the (x-y) plane, are moving out of a uniform magnetic field with a constant velocity \(\vec{v}=v \hat{i}\) The magnetic field is directed along the negative z-axis direction. The induced emf, during the passage of these loops, out of the field region, will not remain
constant for:
(a) any of the four loops
(b) the circular and elliptical loops
(c) the rectangular, circular and elliptical loops
(d) only the elliptical loops
Answer:
(b) the circular and elliptical loops

Explanation: When the loops are being drawn out of the field, the rate at which the number of field lines cutting through the loop decreases will be a constant for square and rectangle loops, but not for circular or elliptical shapes.
Area coming out per second from the magnetic field is not constant for elliptical and circular loops, so induced emf, during the passage of these loops, out of the field region will not remain constant for the circular and the elliptical loops.
Hence option (b) is correct

Question 4.
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is \(\frac{1}{8} \text { th }\) of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to:
(a) .0.80
(b) 0.74
(c) 0.94
(d) 0.85
Answer:
(d) 0.85

In Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is \(\frac{1}{8} \text { th }\) of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to 0.85.
Hence option (d) is correct.

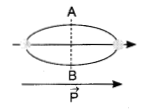
Question 5.
The electric field at a point on equatorial line of a dipole and direction of the dipole moment:
(a) will be parallel
(b) will be in opposite direction
(c) will be perpendicular
(d) are not related
Answer:
(b) will be in opposite direction

Explanation: The direction of electric field at equatorial point A or B will be in opposite direction, as that of direction of dipole moment.

Question 6.
The radius of the innermost electron orbit of a hydrogen atom is 5.3 x 10-11 m. The radius of the n = 3 orbit is:
(a) 1.01 × 10^-10 m
(b) 1.59 × 10^-10 m
(c) 2.12 × 10^-10 m
(d) 4.77 × 10^-10 m
Answer:
(d) 4.77 × 10^-10 m

Explanation: The radius of the innermost orbit of a hydrogen atom, r₁ = 5.3 × 10^-11 m.
The radius of the orbit is proportional to the square of n.
Let r₂ be the radius of the orbit at n = 3.

r₃ = r₁ x 3²
= 5.3 x 10^-11 x 9
= 4.77 x 10^-10 m

Hence, the radii of an electron for n = 3 orbits is 4.77 × 10^-10 m.
Hence option (d) is correct.

Question 7.
According to Coulomb’s law, which is the correct relation for the following figure?

(a) q₁ q₂ >0
(b) q₁ q₂<0
(c) q₁ q₂ = 0
(d) \(1>\frac{q_1}{q_2}>0\)
Answer:
(b) q₁ q₂<0

Explanation: According to the Coulomb’s law, the force of attraction or repulsion between two charged bodies is directly proportional to the product of their charges and inversely proportional to the square of the distance between them. It acts along the line joining the two charges considered to be point charges.

Coulomb’s law holds for stationary charges only, which are point sized. This law obeys Newton’s third law of motion.

F₁₂ = -F₂₁

Here F₁₂ is the force exerted by q₁ on q₂ and F₂₁ is the force exerted by q₂ on q_1.
There is a force of attraction and the charge must be unlike charge. For attractive force, q₁ q₂<0

q₁ = + Ve
q₂=-Ve
q₁ q₂<0

Question 8.
The electric potential on the axis of an electric dipole at a distance Y from it’s centre is V. Then the potential at a point at the same distance on its equatorial line will be: [1]
(a) 2 V
(b) -V
(c) \(\frac{\mathrm{V}}{2}\)
(d) Zero

Explanation: The electric potential at a point due to an electric dipole is given by:

and we know that cos 90° =0.
So, the potential at a point at the same distance on its equatorial line is given by,

\(\mathrm{V}=\frac{k \mathrm{P} \cos 90^{\circ}}{r^2}\)

V =0

Hence option (d) is correct.

Question 9.
The temperature (T) dependence of resistivity of material A and material B is represented by Fig. (i) and Fig. (ii) respectively. Identify material A and material B.

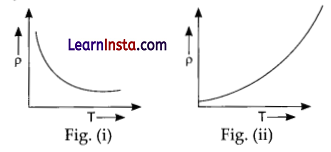
(a) material A is copper and material B is germanium
(b) material A is germanium and material B is copper
(c) material A is nichrome and material B is germanium
(d) material A is copper and material B is nichrome
Answer:
(b) material A is germanium and material B is copper

Explanation: For semiconductors, there are very few free electrons. The conductor’s resistance decreases as a result of an increase in the number of free electrons that can act as carriers as a result of rising temperature [Fig. (i)]
For a conductor, when temperature rises, more free electrons become available. As a result, more of them begin to oppose one another’s motion, increasing the conductor’s resistance [Fig. (ii)]

We know germanium is a semiconductor while copper is a conductor.
So, fig. (i) is a semiconductor while fig. (ii) is a conductor.
Hence, option (b) is correct.

Question 10.
Two concentric and coplanar circular loops P and Q have their radii in the ratio 2 : 3. Loop Q carries a current 9 A in the anti-clockwise direction. For the magnetic field to be zero at the common centre, loop P must carry:
(a) 3A in clockwise direction
(b) 9A in clockwise direction
(c) 6 A in anti-clockwise direction
(d) 6 A in the clockwise direction
Answer:
(d) 6 A in the clockwise direction

Explanation: Given:

Radius (R₁) = 2x
Radius (R₂) = 3x
Current (I₂) = 9 A (anticlockwise)

To find: I₁

We know that the magnetic field at the common centre due to the loop is zero.
So we can say that magnetic field magnitude will be equal but direction is opposite.
Therefore,

B₁=B₂

\(B=\frac{\mu_0 I}{2 R}\)

By using above relation,

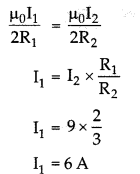
But in opposite direction i.e., clockwise.
Hence,option (d) is correct.

Question 11.
A long straight wire of circular cross-section of radius a carries a steady current I. The current is uniformly distributed across its cross-section. The ratio of the magnitudes of magnetic field at a point distant a/2 above the surface of wire to that at a point distant a/2 below its surface is:
(a) 4:1
(b) 1:1
(c) 4:3
(d) 3:4
Answer:
(c) 4:3

Question 12.
If the magnetizing field on a ferromagnetic material is increased, its permeability:
(c) remains unchanged
(d) first decreases and then increases
(a) decreases
(b) increases
Answer:
(a) decreases

Explanation: The magnetic permeability of a substance is defined as,

μ=B/H
where B is the established magnetic field inside the material and H is the applied external magnetic field.
When the external applied magnetic field H is increased, the established magnetic field for a ferromagnetic material remains the same.
Thus, the magnetic permeability decreases.
Hence option (a) is correct.
(Direction: Question 13 to 16) Two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false and R is false.

Question 13.
Assertion (A): The electrical conductivity of a semiconductor increases on doping.
Reason (R): Doping always increases the number of electrons in the semiconductor.
Answer:
(c) A is true but R is false.

Explanation: This is true that electrical conductivity of a semiconductor increases on doping. In semiconductors, doping can be done with either electron rich or electron deficient impurities. Addition of such impurities cause the electronic defects in a crystal structure, which enhances the electrical conductivity. So, reason is wrong as doping always does not increase, the number of electrons in the semiconductor.
Hence, option (c) is correct.

Question 14.
Assertion (A): In an interference pattern observed in Young’s double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to l/3rd, then new fringe width remains the same.
Reason (R): Fringe width is proportional to (d/D).
Answer:
(c) A is true but R is false.

Explanation: We know that fringe width is proportional to \(\frac{\mathrm{D}}{d}\). In an interference pattern observed in Young’s double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to \(\frac{1}{3} \mathrm{rd}\), then new fringe width remains the same. This is true.

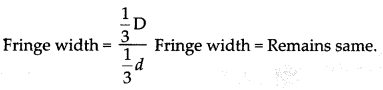
Hence option (c) is correct.

Question 15.
Assertion (A): The photoelectrons produced by a monochromatic light beam incident on a metal surface have a spread in their kinetic energies.
Reason (R): The energy of electrons emitted from inside the metal surface, is lost in collision with the other atoms in the metal.
Answer:(a) Both A and R are true and R is the correct explanation of A.
Explanation: Different photoelectrons emit electrons at various speeds. Actually, not all electrons occupy the same energy level; instead, they do so in a continuous range of levels. As a result, the energy of the electrons that are knocked off at different levels vary.
The energy of electrons emitted from inside the metal surface is lost in collision with the other atoms in the metal.
Hence, option (a) is correct.

Question 16.
Assertion (A): In series LCR resonance circuit, the impedance is equal to the ohmic resistance.
Reason (R): At resonance, the inductive reactance exceeds the capacitive reactance.
Answer:
(a) A is true but R is false.

Explanation: In series resonance circuit, inductive reactance is equal to capacitive reactance.

Section – B

Question 17.
Electromagnetic waves with wavelength:
(i) λ₁ is suitable for radar systems used in aircraft navigation.
(ii) λ₂ is used to improve visibility in runways during fog and mist conditions.
Identify and name the part of the electromagnetic spectrum to which these radiations belong. Also arrange these wavelengths in ascending order of their magnitude.
Answer:
(i) λ₁ → Microwaves are considered suitable for radar systems used in aircraft navigation because they have a short wavelength range ( 10^-3 m to 0.3 m), which makes them suitable for long range communication.
(ii) λ₂ → Infrared rays, Infrared is used to improve visibility on runways during fog and mist conditions. So, it is the wavelength of infrared waves.
Ascending order of wavelength in ascending order:
Wavelength of UV rays < Wavelength of Infrared < wavelength of microwave i.e., λ₂< λ₃< λ₁

Question 18.
A uniform magnetic field gets modified as shown in figure when two specimens A and B are placed in it.

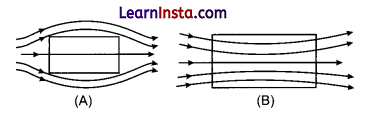
(i) Identify the specimen A and B.
(ii) How is the magnetic susceptibility of specimen A different from that of specimen B?
Answer:
(i) A is diamagnetic and B is ferromagnetic.
(ii) Diamagnetic materials have permeabilities less than 1 (one) and have negative susceptibility. Their atoms and molecules do not have permanent dipole moment. The field lines get expelled in them. Ferromagnetic materials have permeability more than one and susceptibility positive. Their atoms and molecules have permanent dipole moment. So the field lines get concentrated in them.

Question 19.
A biconvex lens made of a transparent material of refractive index 1.25 is immersed in water of refractive index 1.33. Will the lens behave as a converging or a diverging lens? Justify your answer.
Answer:
Generally, a biconvex lens acts as a converging lens in air because the refractive index of air is less than that of the material of the lens. The refractive index of water (1.33) is more than the refractive index of the material of the lens (1.25). So, on immersing in water it will behave as a diverging lens.

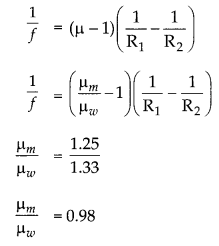
Where f is the focal length of the lens, μ_m is the refractive index of material of lens and μ_ω, is the refractive index of water.
The value of (μ- 1) is negative and focal length ‘f ‘ will be negative. So, it will behave like a diverging lens.

Question 20.
A narrow slit is illuminated by a parallel beam of monochromatic light of wavelength λ equal to 6000 A and the angular width of the central maximum in the resulting diffraction pattern is measured. When the slit is next illuminated by light of wavelength λ’, the angular width decreases by 30%. Calculate the value of the wavelength λ’.

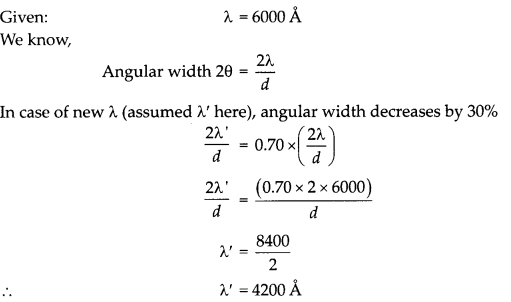
Question 21.
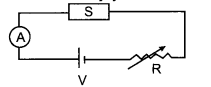
The figure shows a piece of pure semiconductor S in series with a variable resistor R and a source of constant voltage V. Should the value of R be increased or decreased to keep the reading of the ammeter constant, when semiconductor S is heated? Justify your answer:

OR

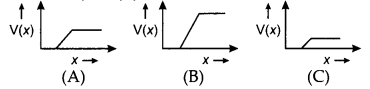
The graph of potential barrier versus width of depletion region for an unbiased diode is shown in graph
A. In comparison to A, graphs B and C are obtained after biasing the diode in different ways. Identify the type of biasing in B and C and justify your answer.

Answer:
As the semiconductors at room temperature act as insulators so they offer a very high resistance value. But with the increase in temperature, they start conducting by decreasing the energy-gap and hence they offer less resistivity. So, the resistivity of semiconductors decreases with the increase in temperature and as a result resistance also decreases. So to maintain the constant reading on the ammeter, we should increase the value of variable resistance R to compensate with the decreased value of resistance for the semiconductor.
Hence, to keep the reading of ammeter constant value of R should be increased as with the increase in temperature of a semiconductor, its resistance decreases and current tends to increase.

OR

In case of reverse biased diodes, the potential barrier becomes higher as the battery further raises the potential of the n-side. The effective barrier height under reverse biased is ( V₀+ V).
C-forward biased
Due to forward bias connection, the potential of the p side is raised and hence the height of the potential barrier decreases therefore, the effective barrier height is reduced to (V₀– V).

Section – C

An a.c. source generating a voltage ε = ε₀ sin ωt is connected to a capacitor of capacitance C. Find the expression for the current I flowing through it. Plot a graph of ε and I versus ωt to show that the current is ahead of the voltage by \(\frac{\pi}{2}\).

OR

An a.c. voltage V = V₀ sin ωt is applied across a pure inductor of inductance L. Find an expression for the current i, flowing in the circuit and show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of \(\frac{\pi}{2}\). Also draw graphs of V and i versus ωt for the circuit.
Answer:
Figure shows an AC source, generating a voltage e = e0 sin ωt, connected to a capacitor of capacitance C. The plates of the capacitor get charged due to the applied voltage. As the alternating voltage is reversed in each half cycle,

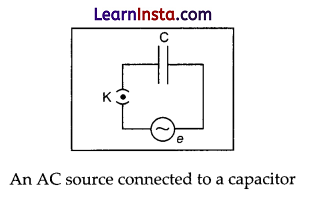
the capacitor is alternatively charged and discharged. If q is the charge on the capacitor, the corresponding potential difference across the plates of the capacitor is V = \(\mathrm{V}=\frac{q}{\mathrm{C}}\)

∴ q = CV.

q and V are functions of time, with V = e = e0 sin ωt. The instantaneous current in the circuit is

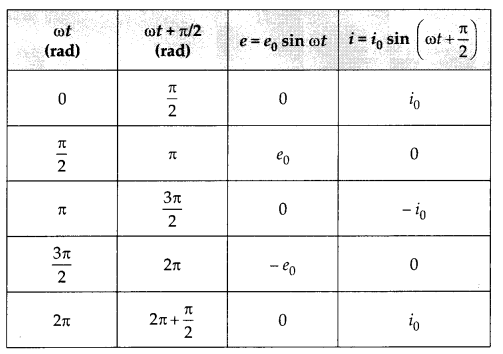
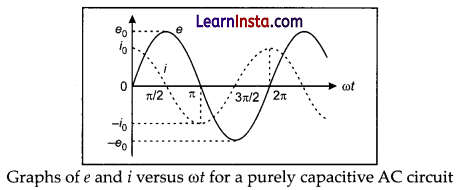
Table gives the values of e and i for different values of cot and Fig. shows graphs of e and i versus ωt. i leads e by a phase angle of π/2 rad.

OR

AC circuit containing pureinductance: Consider a coil of self-inductance Land negligible ohmic resistance. An alternating potential difference is applied across its ends. The magnitude and direction of AC changes periodically, due to which there is a continual change in magnetic flux linked with the coil. Therefore according to Faraday’s law, an induced emf is produced in the coil, which opposes the applied voltage. As a result the current in the circuit is reduced. That is inductance acts like a resistance in ac circuit. The instantaneous value of alternating voltage applied
V = V₀ sin ωt.
If i is the instantaneous current in the circuit and \(\frac{d i}{d t}\) the rate of change of current in the circuit at that instant, then instantaneous induced emf

Where i₀ is the peak value of alternating current.
Also comparing (i) and (iii), we note that current lags behind the applied voltage by an angle 2π.

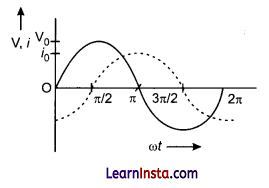
Question 23.
Two long straight parallel conductors carrying currents I₁ and I₂ are separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field produced by one exerts an attractive force on the other. Obtain the expression for this force and hence define 1 ampere.
Answer:

Ampere is that value of steady-state current, which when maintained in each of the very two long, straight, parallel conductors of negligible cross-section and placed lm apart in a vacuum produces 2 × 10^-7 N/m force on each conductor.

Question 24.
The magnetic field through a circular loop of wire, 12 cm in radius and 8.5 Ω resistance, changes with time as shown in the figure. The magnetic field is perpendicular to the plane of the loop. Calculate the current induced in the loop and plot a graph showing induced current as a function of time.

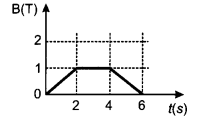
Answer:

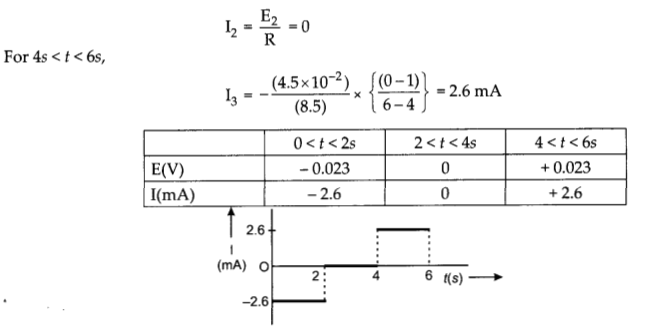
Question 25.
Distinguish between n-type and p-type semiconductors.

	n-type semiconductors	p-type semiconductors
(i)	It is an extrinsic semiconductor obtained by adding a pentavalent impurity to a pure intrinsic semiconductor.	It is also an extrinsic semiconductor obtained by adding a trivalent impurity to a pure intrinsic semiconductor.
(ii)	The impurity atoms added provide extra free electrons to the crystal lattice and are called donor atoms.	The impurity atoms added create holes in the crystal lattice and are called acceptor atoms.
(iii)	The electrons are majority carriers and the holes are minority carriers.	The holes are majority carriers and the electrons are minority carriers.
(iv)	The electrons concentration is much more than the hole concentration (ne» nh).	The hole concentration is much more than the electron concentration (nh » ne).

Question 26.
The graph shows the variation of photocurrent for a photosensitive metal:

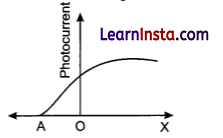
(a) What does X and A on the horizontal axis represent?
(b) Draw this graph for three different values of frequencies of incident radiation v₁, v₂ and v₃ (v₃ > v₂ > v₁) for the same intensity.
(c) Draw this graph for three different values of intensities of incident radiation I₁, I₂ and I₃ (I₃ > I₂ > I₁) having the same frequency.
Answer:
(a) A- cut off or stopping potential
X- anode potential

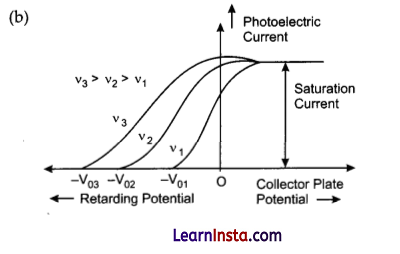
Variation of photoelectric current with collector plate potential for different frequencies of incident radiation

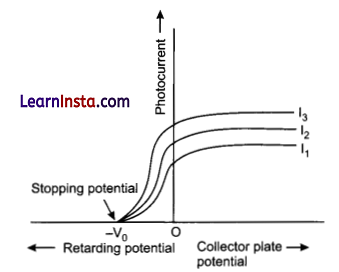
Variation of photocurrent with collector plate potential for different intensity of incident radiation.

Question 27.
The ground state energy of hydrogen atom is -13.6 eV. The photon emitted during the transition of electron from n = 3 to n =1 state, is incident on a photosensitive material of unknown work function. The photoelectrons are emitted from the material with the maximum kinetic energy of 9 eV. Calculate the threshold wavelength of the material used.
Answer:
A transition from n = 3 to n = 1 state, the energy of the emitted photon

Question 28.
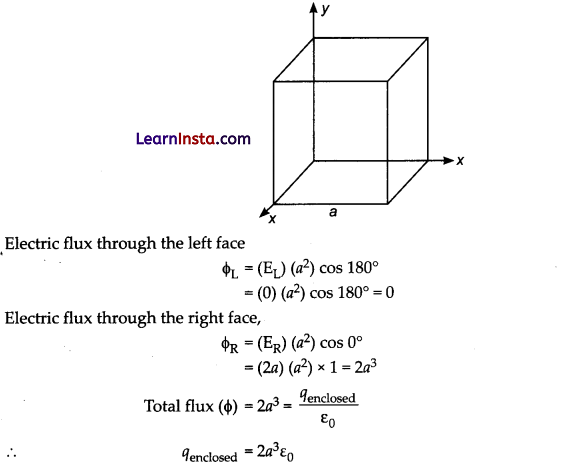
Given the electric field in the region \(\overrightarrow{\mathrm{E}}=2 \hat{x} l\), find the net electric flux through the cube and the charge enclosed by it.
OR
A thin metallic spherical shell of radius carries a charge Q on its surface. A point charge is placed at its centre C and another charge + 2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find
(i) the force on the charge at the centre of shell and at the point A.
(ii) the electric flux through the shell.

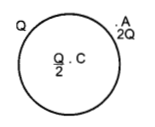
Answer:
Since, the electric field is parallel to the faces parallel to xy and xz planes, the electric flux through them is zero.

Section – D

Question 29.
Read the passage given below and answer the following questions:
Electromagnetic waves are produced by acceleration of charges. These are non mechanical waves so these waves do not require any kind of material medium for propagation. The speed of these waves in free space is equal to the speed of light. These waves are the sinusoidal variation in the magnetic as well as electric field vectors \((\vec{E} \text { and } \vec{B})\). Electromagnetic waves are transverse in nature. The velocity of electromagnetic waves in the dielectrics is always less than the speed of light \(\left(c=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right)\).
The energy of electromagnetic waves is equally divided between electric field and magnetic field vectors.
In these waves, the electric vector is responsible for optical effects of electromagnetic waves. So electric vector is also called light vector.
(i) Which of the following e.m. wave has highest wavelength?
(a) X-ray
(b) UV rays
(c) infrared rays
(d) microwaves
Answer:
(d) microwaves

OR

Who first demonstrated the existence of e.m. waves:
(a) Hertz
(b) Maxwell
(c) Ampere
(d) Faraday
Answer:
(a) Hertz

(ii) The dimensions of E/B are same as that of:
(a) charge
(b) current
(c) velocity
(d) acceleration
Answer:
(c) velocity

(iii) An e.m. wave of frequency, v = 3 MHz passes from vacuum into dielectric medium with permittivity E_r = 4, then:
(a) wavelength is doubled and frequency is unchanged.
(b) wavelength is doubled and frequency becomes half.
(c) wavelength is halved and frequency remains unchanged.
(d) wavelength and frequency both remains unchanged.
Answer:
(c) wavelength is halved and frequency remains unchanged.

(iv) If u_e and u_m are the electric and magnetic field densities in an electromagnetic wave, then c is the speed of light:
(a) u_e = u_m
(b) u_e = cu_m
(c) \(u_e=\frac{u_m}{c}\)
(d) None of these
Answer:
(a) u_e = u_m

Question 30.
Energy Band Gap
From Bohr’s atomic modal, we know that the electrons have well defined energy levels in an isolated atom. But due to interatomic interactions in a crystal, the electrons of the outer shells are forced to have energies different from those in isolated atoms. Each energy levels splits into a number of energy forming a continuous band. The gap between top of valence band bottom of the conduction band in which no allowed energy levels for electrons can exist is called energy gap.

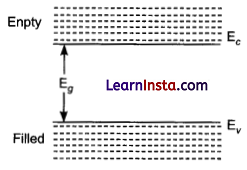
(i) In an insulator energy band gap is:
(a) E_g = 0
(b) E_g < 3 eV
(c) E_g > 3 eV
(d) None of these
Answer:
(c) E_g > 3 eV

(ii) In a semiconductor, separation between conduction and valence band is of the order of
(a) 0 eV
(b) 1 eV
(c) 10 eV
(d) 50 eV
Answer:
(b) 1 eV

(iii) Based on the band theory of conductors, insulators and semiconductors, the forbidden gap is smallest in
(a) conductors
(b) insulators
(c) semiconductors
(d) all of these
Answer:
(a) conductors

(iv) Carbon, silicon and germanium have four valence electrons each. At room temperature which one of the following statements is most appropriate?
(a) The number of free electrons for conduction is significant only in Si and Ge but small in C.
(b) The number of free conduction electrons is significant in C but small in Si and Ge.
(c) The number of free conduction electrons is negligibly small in all three.
(d) The number of free electrons for conduction is significant in all the three.
Answer:
(a) The number of free electrons for conduction is significant only in Si and Ge but small in C.

OR

Solids having highest energy level partially filled with electrons are
(a) semiconductor
(b) conductor
(c) insulator
(d) none of these
Answer:
(b) conductor

Section – E

Question 31.
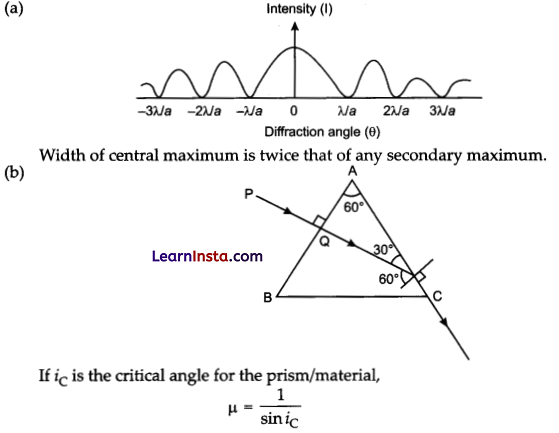
(a) Draw the graph showing intensity distribution of fringes with phase angle due to diffraction through a single slit. What is the width of the central maximum in comparison to that of a secondary maximum?
(b) A ray PQ is incident normally on the face AB of a triangular prism of refracting p angle 60° as shown in figure. The prism is made of a transparent material of refractive index \(\frac{2}{\sqrt{3}}\). Trace the path of the ray as it passes through the prism.

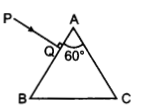
Calculate the angle of emergence and the angle of deviation.
OR
(a) Write two points of difference between an interference pattern and a diffraction pattern.
(b) (i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30°. Calculate the speed of light through the prism.

 

(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
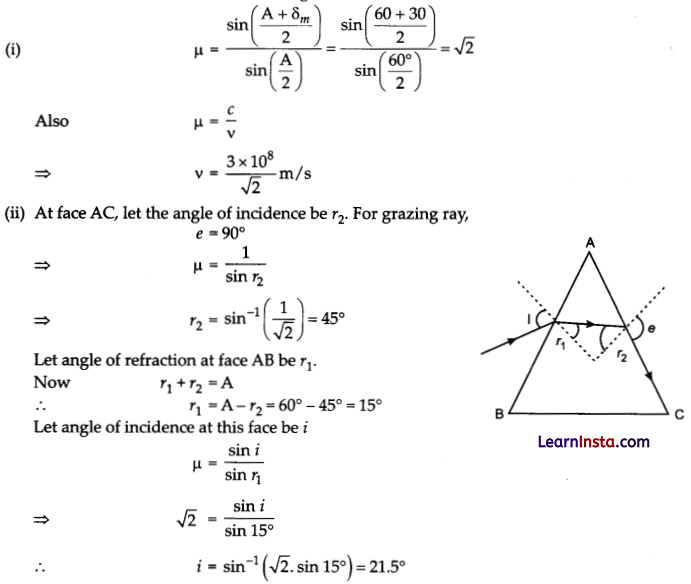
Answer:

\(\sin i_C=\frac{1}{\mu}=\frac{\sqrt{3}}{2}\)

⇒ i_c = 60°
Angle of incidence at face AC of the prism = 60°
Hence, refracted ray grazes the surface AC.
⇒ Angle of emergence = 90°
⇒ Angle of deviation = 30°

OR

(a) (i) The interference pattern has a number of equally spaced bright and dark bands. The diffraction pattern has a central bright maximum which is twice as wide as the other maxima. The intensity falls as we go to successive maxima away from the centre, on either side.
(ii) We calculate the interference pattern by superposing two waves originating from the two narrow slits. The diffraction pattern is a superposition of a continuous family of waves originating from each point on a single slit.

Question 32.
(a) Draw equipotential surfaces for (i) an electric dipole and (ii) two identical positive charges placed near each other.
(b) In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10^-3 m² and the separation between the plates is 3 mm.
(i) Calculate the capacitance of the capacitor.
(ii) If the capacitor is connected to 100V supply, what would be the charge on each plate?
(iii) How would charge on the plate be affected if a 3 mm thick mica sheet of k = 6 is inserted between the plates while the voltage supply remains connected?
OR
(a) Three charges -q,Q and- q are placed at equal distances on a straight line. If the potential energy of the system of these charges is zero, then what is the ratio Q: q?
(b) (i) Obtain the expression for the electric field intensity due to a uniformly charged spherical shell of radius R at a point distant r from the centre of the shell outside it.
(ii) Draw a graph showing the variation of electric field intensity E with r, for r > R and r < R.
Answer:
(a) (i) a dipole

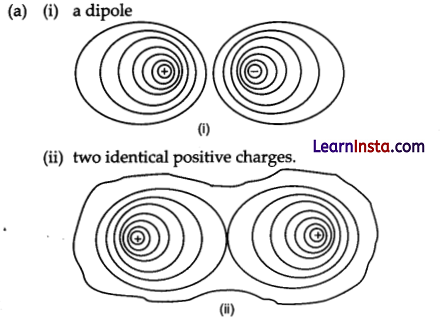
(b) In a parallel plate capacitor(ii) with air between the plates, each plate has an area of 6 × 10^-3 m² and the separation between the plates is 3 mm.

Here, A = 6 × 10^-3 m², d = 3mm = 3 × 10^-3m

(i) Capacitance, \(\mathrm{C}=\frac{\varepsilon_0 \mathrm{~A}}{d}=\left(\frac{8.85 \times 10^{-12} \times 6 \times 10^{-3}}{3 \times 10^{-3}}\right)=17.7 \times 10^{-12} \mathrm{~F}\)

(ii) Charge, Q = CV =17.7 × 10^-12 × 100 = 17.7 × 10^-10 C
(iii) New charge Q’ = KQ = 6 × 17.7 × 10^-10 = 1.062 × 10^-8 C

OR

(a) We know potential energy is a scalar quantity

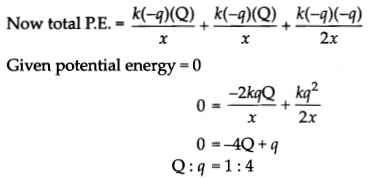
(b) Consider a thin spherical shell of radius R with a positive charge q distributed uniformly on the surface. As the charge is uniformly distributed, the electric field is symmetrical and directed radially outward.

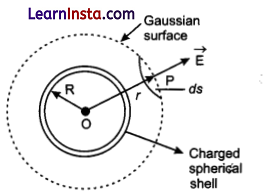
(i) When point P lies outside the spherical shell: Suppose that we have calculated the field at the point P at a distance r(r > R) from its centre. Draw Gaussian surface through point P so as to enclose the charged spherical shell. The Gaussian surface is a spherical surface of radius r and centre O.

Let E be the electric field at point P, then the electric flux through area element of area ds is given by

Question 33.
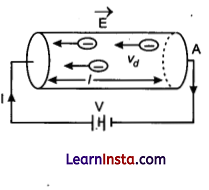
(a) Explain the term drift velocity of electrons in a conductor. Hence obtain the expression for the current through a conductor in terms of drift velocity.
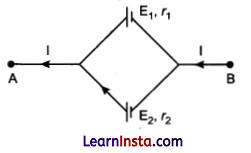
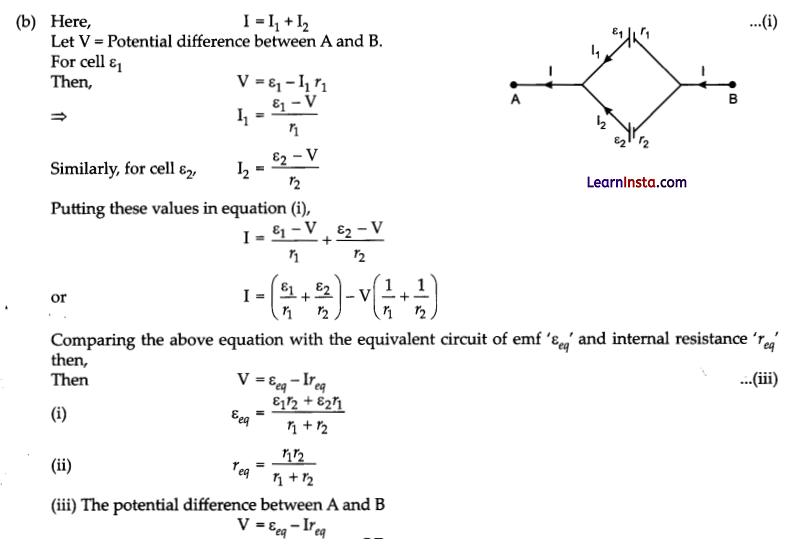
(b) Two cells of emfs E₁ and E₂ and internal resistances r₁ and r₂ respectively are connected in parallel as shown in the figure.
Deduce the expression for the:
(i) equivalent emf of the combination.
(ii) equivalent internal resistance of the combination.
(iii) potential difference between the points A and B.

OR
(a) State the two Kirchhoff’s rules used in the analysis of electric circuits and explain them.
(b) Derive the equation of the balanced state in a Wheatstone bridge using Kirchhoff’s laws.
Answer:
(a) Drift velocity: It is the average velocity acquired by the free electrons superimposed over the random motion in the direction opposite to electric field and along the length of the metallic conductor.
If e is the magnitude of charge on each electron, then the total charge in the conductor,

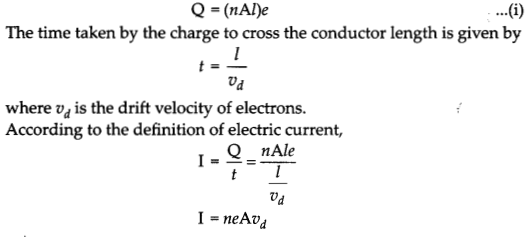
OR

(a) (i) Kirchhoff’s first law (junction rule): In an electrical circuit, the algebraic sum of currents meeting at a junction is always zero.
(ii) Kirchhoff’s second rule (loop rule): In any closed mesh of an electrical circuit, the algebraic sum of the e.m.fs. is equal to the algebraic sum of products of resistances and current flowing through them.
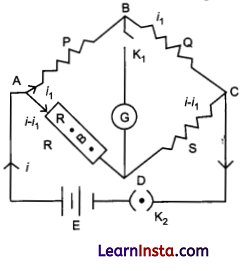
(b) Wheatstone bridge (balanced): Let i be the current from battery E. At point A, current i₁ flows through resistance P and current i – i₁ flows through R.

In balanced state, no current flows through BD, hence point B and D are at same potential.
Therefore, current i₁ flows through resistance Q also and current i – i₁ flows through S. Applying Kirchhoff’s loop rule in closed mesh ABDA,
i₁P- (i– i₁) R = 0 or i₁P = (i– i₁)R …………… (i)

In closed mesh BCDB,
i₁Q-(i– i₁)S=O or i₁Q = (i– i₁)S …………….(ii)

Dividing (i) from (ii), we get

\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)

This is the condition for balance in a Wheatstone’s bridge