Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Set 3 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 12 Physics Set 3 with Solutions
Time : 3 Hours
Maximum Marks: 70
General Instructions :
- There are 33 questions in all. All questions are compulsory.
- This question paper has five sections: Section A, Section B, Section C. Section D and Section E.
- Air the sections are compulsory.
- Section A contains sixteen questions, twelve MCQ and four Assertion-Reasoning based questions of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study-based questions of four marks each and Section E contains three long answer questions of five marks each.
- There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
- Use of calculators is not allowed.
- You may use the following values of physical constants wherever necessary
(i) c = 3 ×108 m/s
(ii) me = 9.1 × 10-31 kg
(iii) e = 1.6 × 10-19 C
(iv) μ0= 4π × 10-17 TmA-1
(v) h = 6.63 × 10-34 Js
(vi) ε0 = 8.854 ×10-12 C2N-1m-2
(vii) Avogadro’s number = 6.023 × 1023 per gram mole
Section – A
The following questions are multiple-choice questions with one correct answer. Each question carries 1 mark. There is no internal choice in this section.
Question 1.
One metallic sphere A is given positive charge whereas another identical metallic sphere B of exactly same mass as of A is given equal amount of negative charge. Then:
(a) mass of A and mass of B still remain equals and same
(b) mass of A increases
(c) mass of B decreases
(d) mass of B increases
Answer:
(d) mass of B increases
Explanation: Negative charge means excess of electrons which increases the mass of sphere B, whereas positive charge on sphere A is given fay removal of electrons.
Question 2.
The physical quantity having SI unit NC-1 m is:
(a) Electric potential
(b) Electric force
(c) Electric field intensity
(d) None of these
Answer:
(a) Electric potential
Explanation: V = E.d = NC-1 m
![]()
Question 3.
The I-V characteristics shown in figure represents:
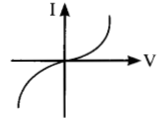
(a) ohmic conductors
(b) non-ohmic conductors
(c) insulators
(d) superconductors
Answer:
(b) non-ohmic conductors
Explanation: The figure is showing I-V characteristics of non-ohmic or non-linear conductors.
Question 4.
A current I flows through a long straight conductor which is bent into a circular loop of radius R in the middle as shown in the figure.
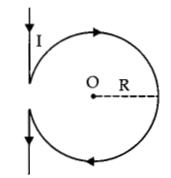
The magnitude of the net magnetic field at point O will be :
(a) Zero
(b) \(\frac{\mu_0 \mathrm{I}}{2 \mathrm{R}}(1+\pi)\)
(c) \(\frac{\mu_0 I}{2 \pi R}\)
(d) \(\frac{\mu_0 I}{2 R}\left(1-\frac{1}{\pi}\right)\)
Answer:
(d) \(\frac{\mu_0 I}{2 R}\left(1-\frac{1}{\pi}\right)\)
Explanation: Net magnetic field at point
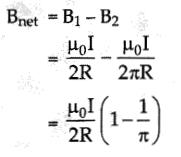
Question 5.
A proton of mass m and charge q is moving in a plane with kinetic energy E. If there exists a uniform magnetic field B, perpendicular to the plane of the motion, the proton will move in a circular path of radius:
(a) \(\frac{2 \mathrm{E} m}{q \mathrm{~B}}\)
(b) \(\frac{\sqrt{\mathrm{Em}}}{2 q \mathrm{~B}}\)
(c) \(\frac{\sqrt{2 \mathrm{E} m}}{q \mathrm{~B}}\)
(d) \(\frac{\sqrt{2 \mathrm{E} q}}{m \mathrm{~B}}\)
Answer:
(c) \(\frac{\sqrt{2 \mathrm{E} m}}{q \mathrm{~B}}\)
![]()
Question 6.
When a ferromagnetic substance is heated above Curie temperature, then :
(a) it is demagnetised
(b) it becomes diamagnetic
(c) it becomes paramagnetic
(d) it remains unaffected
Answer:
(c) it becomes paramagnetic
Explanation: When a ferromagnetic substance is heated to a very high temperature it looses its magnetic property Ferromagnetic substances becomes paramagnetic. This happens because of the disordemess of the electron arrangement.
Question 7.
In an AC circuit I = 100 sin 200πt. The time required for the current to achieve its peak value will be:
(a) \(\frac{1}{200} \mathrm{~s}\)
(b) \(\frac{1}{400} \mathrm{~s}\)
(c) \(\frac{1}{100} \mathrm{~s}\)
(d) \(\frac{1}{300} \mathrm{~s}\)
Answer:
(b) \(\frac{1}{400} \mathrm{~s}\)
Explanation: The current takes \(\frac{\mathrm{T}}{4}\) s to reach the peak value.
In the given question,

Question 8.
If E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of
propagation of electromagnetic wave is along :
(a) E
(b) B
(c) B × E
(d) E × B
Answer:
(d) E × B
Explanation: The direction of propagation of electromagnetic wave is perpendicular to both electric field vector E and magnetic field vector B, i.e., in the direction of E × B. This can be seen by the diagram given below:
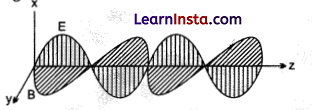
Here, electromagnetic wave is along the z-direction which is given by the cross product of E and B.
Question 9.
The magnetic flux through a circuit of resistance R changes by an amount A<|) in a time At. then the total quantity of electric charge Q that passes through any point in the circuit during the time At is represented by:
(a) \(\mathrm{Q}=\frac{\Delta \phi}{\mathrm{R}}\)
(b) \(\mathrm{Q}=\mathrm{R} \frac{\Delta \phi}{\Delta t}\)
(c) \(\mathrm{Q}=\frac{1}{\mathrm{R}} \cdot \frac{\Delta \phi}{\Delta t}\)
(d) \(\mathrm{Q}=\frac{\Delta \phi}{\Delta t}\)
Answer:
(a) \(\mathrm{Q}=\frac{\Delta \phi}{\mathrm{R}}\)
Explanation:

![]()
Question 10.
A beam of electrons is used in Young’s double slit experiment. If. the speed of electrons is increased, then the fringe width will :
(a) increase
(b) decrease
(c) remain same
(d) fringes will not be seen
Answer:
(b) decrease
Explanation: For electron,

so, higher the velocity lower the fringe width.
Question 11.
Photons of frequency v are incident on the surfaces of metals A and B of threshold frequencies and , respectively. The ratio of the maximum kinetic energy of electrons emitted from A to that from B is:
(a) 2:3
(b) 4:3
(c) 3:4
(d) 3:2
Answer:
(c) 3:4
Explanation: According to Einstein photoelectric equation

Question 12.
In an unbiased p-n junction, holes diffuse from the p-region to n-region because:
(a) free electrons in the n-region attract them.
(b) they move across the junction by the potential difference.
(c) hole concentration in p-region is more as compared to n-region.
(d) All the above.
Answer:
(c) hole concentration in p-region is more as compared to n-region.
Explanation: The diffusion of charge carriers across a junction occurs from the region of higher concentration to the region of lower concentration. Thus, the p-region has greater concentration of holes than the n-region. Hence, in an unbiased p-n junction, holes diffuse from the p-region to the n-region.
(Direction: Question 13 to 16) Two statements are given-one labelled Assertion (A) and the other labelled
Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below:
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is not the correct explanation of A.
(c) A is true, but R is false.
(d) A is false and R is also false.
![]()
Question 13.
‘Assertion: If the temperature of a semiconductor is increased then it’s resistance decreases.
Reason: The energy gap between conduction band and valence band is very small.
Answer:
(a) Both A and R are true and R is the correct explanation of assertion.
Explanation: In semiconductors, the energy gap between conduction band and valence band is smaH (a1 eV). Due to temperature rise, electron in the valence band gain thermal energy and may jump across the small energy gap (to the conduction band). Thus, conductivity increases and hence resistance decreases.
Question 14.
Assertion: Intensity pattern of interference and diffraction are not same.
Reason: When there are few sources of light, then the result is usually called diffraction but if there is a large number of them, the word interference is more often used.
Answer:
(c) A is true, but R is false.
Explanation: When there are few sources of light, then the result is usually called interference but if there is a large number of them, the word diffraction is more often used.
Question 15.
Assertion: Photoelectric effect demonstrates the wave nature of light.
Reason: The number of photoelectrons is proportional to the frequency of light.
Answer:
(d) A is false and R is also false.
Explanation: Photoelectric effect demonstrates particle nature of light. Number of emitted photoelectrons depends upon intensity of light.
Question 16.
Assertion: Lenz’s law is based on the principle of conservation of energy.
Reason: Induced emf always opposes the change in magnetic flux responsible for its production.
Answer:
(a) Both A and R are true and R is the correct explanation of A.
Explanation: Lenz’s Law is based on conservation of energy and induced emf opposes the cause of it i.e., change in magnetic flux.
Section – B
Question 17.
How are e.m. waves produced by oscillating charges?
Draw a sketch of linearly polarized e.m. waves propagating in the Z-direction. Indicate the directions of the oscillating electric and magnetic fields.
Answer:
A charge oscillating with some frequency, produces an oscillating electric field in space, which in turn produces an oscillating magnetic field perpendicular to the electric field, this process goes on repeating, producing e.m. waves in space perpendicular to both the fields.

The direction of electric and magnetic fields are perpendicular to each other and are also perpendicular to the direction of propagation of the wave.
Question 18.
(i) Write the expression for the force \(\overrightarrow{\mathrm{F}}\) acting on a particle of mass m and charge q moving with velocity \(\vec{v}\) in a magnetic field \(\overrightarrow{\mathrm{B}}\). Under what conditions will it move in (a) a circular path and (b) a helical path?
(ii) Show that the kinetic energy of the particle moving in magnetic field remains constant.
Answer:
(i)\(\overrightarrow{\mathrm{F}}=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)
= qvB sin θ
Conditions:
(a) If the angle between v and B is 90° then it will move in circular path.
(b) If the angle is other than, 0°, 90° and 180° the path will be helical.
(ii) Since the work done on the charged particle moving in the magnetic field is zero. Hence, according to work energy theorem the change in kinetic energy is zero.
![]()
Question 19.
An equilateral glass prism has a refractive index 1.6 in air. Calculate the angle of minimum deviation of the ‘ prism, when kept in a medium of refractive index 4√2/5.
Answer:
As we know,
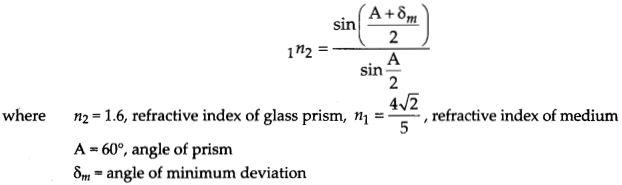
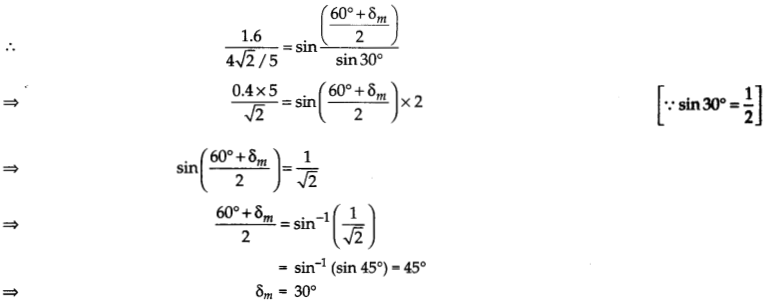
Question 20.
Monochromatic light of wavelength 589 nm is incident from air on a water surface. If p for water is 1.33, find the wavelength, frequency and speed of the refracted light.
Answer:

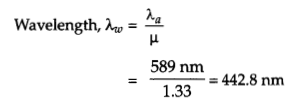
![]()
Question 21.
Define the V-I characteristics of a junction diode.
OR
Graph showing the variation of current versus voltage for a material Ga-As is shown in the figure. Identify the region of:
(i) negative resistance
(ii) where Ohm’s law is obeyed
Answer:
The V-I characteristic of the diode is the graph drawn between the voltage, V and current I in forward bias and reverse bias of junction diode.
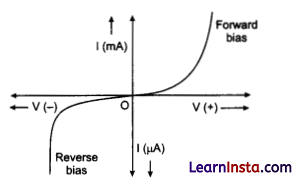
(i) DE is the region of negative resistance because the slope of curve in this part is negative.
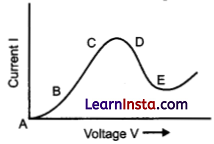
(ii) BC is the region where Ohm’s law is obeyed because in this part, the current varies linearly with the voltage.
Section – C
Question 22.
A series LCR circuit with R = 20 Ω, L = 1.5 H and C = 35 μF is connected to a variable frequency 200 V a.c. supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
OR
Obtain the resonant frequency and Q-factor of a series LCR circuit with L = 3.0 H, C = 27 μF and R = 7.4 Ω. It is desired to improve the sharpness of the resonance of the circuit by reducing its full width at half maximum by a factor of 2. Suggest a suitable way.
Answer:
At resonance, the frequency of the supply power equals the natural frequency of the given LCR circuit.
Given: Resistance, R = 20 Ω, inductance, L = 1.5 H, capacitance, C = 35 μF = 35 × 10-6 F
AC supply voltage to the LCR circuit, V = 200 V
Impedance of the circuit is given by the relation,
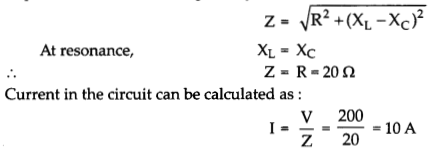
Thus, the average power transferred to the circuit is one complete cycle :
P = VI = 200 × 10 = 2000 W
OR
Given, Inductance (L) = 3.0 H
Capacitance (C) = 27 pF = 27 × 10-6 F
Resistance (R) = 7.4 Ω
At resonance, angular frequency of the source for the given LCR series circuit is given by
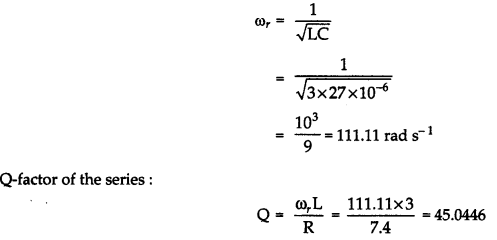
To improve the sharpness of the resonance by reducing its ‘full width at half maximum’ by a factor of 2 without changing (ωr) we need to reduce R to half i.e., resistance = \(\frac{R}{2}=\frac{7.4}{2}=3.7 \Omega\)
![]()
Question 23.
Write using Biot-Savart law, the expression for the magnetic field \(\overrightarrow{\mathrm{B}}\) due to an element \(\overrightarrow{d l}\) carrying current I at a distance \(\vec{r}\) from it in a vector form.
Hence derive the expression for the magnetic field due to a current carrying loop of radius R at a point P distant X from its centre along the axis of the loop.
Answer:
Suppose we have a conductor of length l in which current i is flowing. We need to calculate the magnetic field at a point P in vacuum. If \(\overrightarrow{i d l}\)is one of the infinitely small current element, the magnetic field d B at a at point P is given by
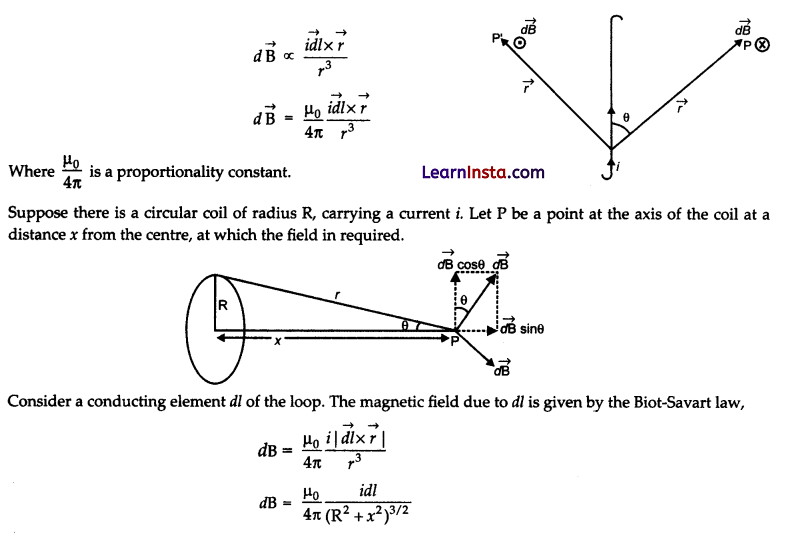
The direction of dB is perpendicular to the plane formed by dl and r. It has an X-component dBx and a component perpendicular to X-axis, dB±. When the components perpendicular to the X-axis are summed over, they cancel out and we obtain null result. Thus, only the X-component survives.
So the resultant field \(\overrightarrow{\mathrm{B}}\) at P is given by
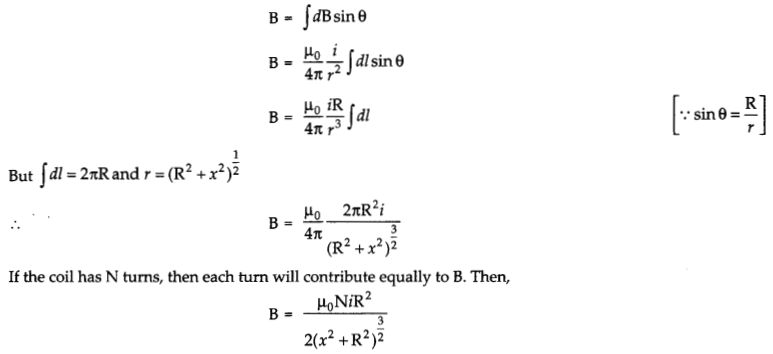
![]()
Question 24.
A rectangular loop of wire of size 4 cm x 10 cm carries a steady current of 2 A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find :
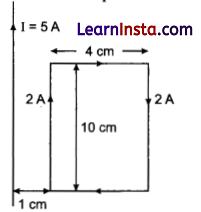
(i) the magnitude and direction of the force on the loop due to the current carrying wire.
(ii) the torque acting on the loop.
Answer:
(i) From the direction of current flow the force on each side of loop are as per fig. FAB and FQC are equal and opposite so they will cancel each other.
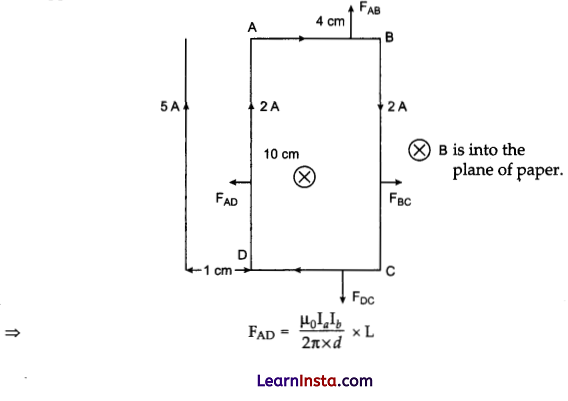

The direction of net force is towards the straight wire i.e., attractive.
(ii) Torque will be zero as all the forces are in the plane of loop.
Question 25.
If light of wavelength 412.5 nm is incident on each of the metals given below, which one will show photoelectric emission and why?
| Metal | Work Function (eV) |
| Na | 1.92 |
| K | 2.15 |
| Ca | 3.20 |
| Mo | 4.17 |
Answer:
Wavelength of incident light,
λ = 412.5 nm
= 412.5 × 10-9m
∴ Energy of incident light
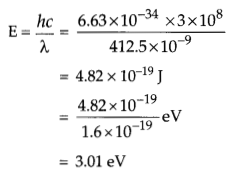
Since, the energy of incident radiation is greater than the work function of sodium and potassium, but less than that of calcium and molybdenum, therefore, photoelectric emission will take place in sodium and potassium.
![]()
Question 26.
In an intrinsic semiconductor the energy gap E? is 1.2 eV. Its hole mobility is much smaller than electron mobility and independent of temperature. What is the ratio between conductivity at 600 K and that 300 K? Assume that the temperature dependence of intrinsic carrier concentration n, is given by
Where no is constant.
Answer:
Given, energy gap of the intrinsic semiconductor (Eg) = 1.2 eV.
The temperature dependence of the intrinsic carries concentration is given by
Here, ko = Boltzmann constant = 8.62 × 10-5 eV/K
(T = Temperature, no = Constant)
Initial temperature (T1) = 300K.
The intrinsic carrier-concentration at this temperature can be given by
\(n_1=n_0 \exp \left[-\frac{\mathrm{E}_g}{2 k_{\mathrm{B}} \times 300}\right]\)
Final temperature (T2) = 600K.
The intrinsic carrier-concentration at this temperature can be given as
\(n_2=n_0 \exp \left[-\frac{\mathrm{E}_g}{2 k_{\mathrm{B}} \times 600}\right]\)
The ratio between the conductivity at 600 K and at 300 K is equal to the ratio between the respective intrinsic carrier-concentrations at these temperature.
Question 27.
A thin metallic spherical shell of radius carries a charge Q on its surface. A point charge is placed at its centre C and another charge + 2Q is placed outside the shell at a distance x from the centre as shown in the figure. Find
(i) the force on the charge at the centre of shell and at the point A
(ii) the electric flux through the shell.
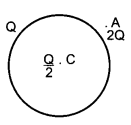
Answer:

Question 28.
(i) How is the stability of hydrogen atom in Bohr model explained by de-Broglie’s hypothesis?
(ii) A hydrogen atom initially in the ground state absorbs a photon which excites it to n = 4 level. When it gets de-excited, find the maximum number of lines which are emitted by the atom. Identify the series to which these lines belong. Which of them has the shortest wavelength?
OR
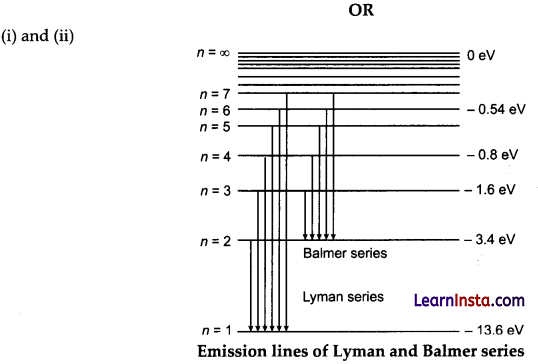
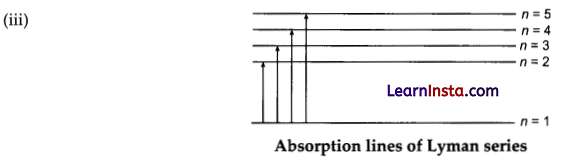
On an energy level diagram of hydrogen, show by a downward or an upward arrow transition which results in :
(i) emission line of Balmer series.
(ii) emission line of Lyman series.
(iii) absorption line of Lyman series.
Answer:
(i) From Bohr’s model-an atom has a number of stable orbits in which an electron can reside without the emission of radiant energy. Each orbit corresponds to a certain energy level. Electron revolves is circular orbit

The motion of an electron in circular orbits is restricted in such a manner that its angular momentum is an integral multiple of \(\frac{h}{2 \pi}\)

Section – D
Question 29.
Read the passage given below and answer the following questions:
Young’s double slit experiment was done by Thomas Young to demonstrate experimentally the interference of light. In this, coherent sources of monochromatic light are used. Here two sources of monochromatic light are obtained by placing two slits before a single light source. As light rays passes from the slits the interference of light takes place. The interference fringes are obtained on the screen. The fringe obtained at the centre of screen is a bright fringe
Fringe width (β) = \(\frac{\lambda \mathrm{D}}{d}\)
Where β-Fringe width, D- Distance between screen and slit, d- Distance between slits.
(i) What kind of light sources are used in this experiment?
(a) Monochromatic
(b) Trichromatic
(c) Dichromatic
(d) Any
Answer:
(a) Monochromatic
OR
How many slits are used in this experiment?
(a) Two
(b) One
(c) Three
(d) Many
Answer:
(a) Two
![]()
(ii) The central fringe in the experiment is:
(a) Dark
(b) Very dark
(c) Bright
(d) None of these
Answer:
(c) Bright
(iii) What kind of phenomena of light is demonstrated with this experiment?
(a) Reflection
(b) Refraction
(c) Interference
(d) Diffraction
Answer:
(c) Interference
(iv) What will be the ratio of fringe width β1 and β2 obtained with red light of λ1 = 660 nm and ultraviolet light of λ2 = 165 nm
(a) 1:4
(b) 4:1
(c) 2:1
(d) 1:2
Answer:
(b) 4 : 1
Question 30.
Read the passage given below and answer the following questions:
Rutherford’s model of atom : This model of atom was given by Rutherford. According to him each atom have tiny core at its centre which is called nucleus of the atom..In the nucleus whole mass and positive charge of the nucleus is concentrated. The size of the nucleus is of the order of 10-15 m and atomic size is about 10-10 m.
The nucleus of the atom is surrounded by a number of electrons. But whole atom is electrically neutral. These electrons revolve in certain orbits around the nucleus of an atom the electrons get centripetal force from the electrostatic force between nucleus and electrons.
(i) The tiny core at the centre of atom is:
(a) Electron
(b) Atom
(c) Nucleus
(d) Proton
Answer:
(c) Nucleus
(ii) Whole mass of the atom is concentrated at:
(a) Periphery of atom
(c) Nucleus
(b) Proton
(d) None of these
Answer:
(c) Nucleus
(iii) The size of the nucleus is of the order of:
(a) 1015m
(b) 10“5m
(c) 10″15m
(d) 1010m
Answer:
(c) 10-15m
![]()
(iv) The nucleus of the atom is surrounded by a number of:
(a) Protons
(b) Neutrons
(c) Electrons
(d) None of these
Ans:
(c) Electrons
OR
Atom is electrically:
(a) Positive
(b) Negative
(c) Earthed
(d) Neutral
Answer:
(d) Neutral
Section – E
Question 31.
(a) You are given three capacitors of 2 μF, 3 μF and 4 μF, respectively.
(i) Form a combination of all these capacitors of equivalent capacitance \(\frac{13}{3}\) μF.
(ii) What is the maximum and minimum value of the equivalent capacitance that can be obtained by connecting these capacitors?
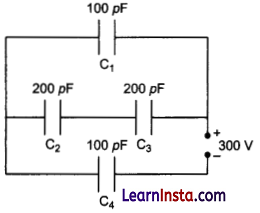
(b) Obtain the equivalent capacitance of the network in Fig. For a 300 V supply, determine the charge and voltage across each capacitor.
OR
(a) A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 360 μC. When potential across the capacitor is reduced by 120 V, the charge stored in it becomes 120 μC.
Calculate :
(i) The potential V and unknown capacitance C.
(ii) What will be the charge stored in the capacitor, if the voltage applied had increased by 120 V?
(b) Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination.
Answer:
(a) Given, capacitor are 2 μF, 3 μF and 4 μF.
(i) The combination of 2 μF and 4 μF in series with 3 μF in parallel.
\(\frac{1}{\mathrm{C}_s}=\frac{1}{2}+\frac{1}{4}\)

(ii) Maximum capacitance can be achieved by joining the capacitors in parallel.
i.e., Cmax = 2 + 3 + 4 = 9μF
Minimum capacitance is achieved by joining the capacitors in series.
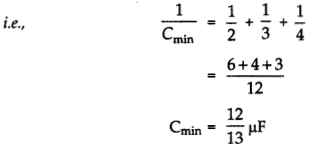
(b) Capacitance of capacitor C1 is 100 pF.
Capacitance of capacitor C2 is 200 pF.
Capacitance of capacitor C3 is 200 pF.
Capacitance of capacitor C4 is 100 pF.
Supply potential, V = 300 V
Capacitors C2 and C3 are connected in series. Let their equivalent capacitance be C’
∴ \(\frac{1}{\mathrm{C}^{\prime}}=\frac{1}{200}+\frac{1}{200}=\frac{2}{200}\)
C = 100 pF
Capacitors Q and C’ are in parallel. Let their equivalent capacitance be C”.
C’=C1 + C1
= 100 + 100 = 200 pF
C” and C4 are connected in series. Let their equivalent capacitance be C.

Potential difference across C” = V”
Potential difference across C4 = V4
V” + V4= V = 300 V
Charge on C4 is given by,
Q4 = CV (As C4 and C” are in series then they have same charge = Q4)
\(=\frac{200}{3} \times 10^{-12} \times 300\)

OR

(ii) If the voltage applied had increased by 120 V, then
V3 = 180 + 120 = 300 V
Hence charge stored in capacitor,
Q3 = cv3 = 2 × 10-6 × 300 = 600 μC
(b) When the capacitors are connected in parallel.
Equivalent capacitance,
Cp = C1 + C2
The energy stored in the combination of the capacitors,

Solving (i) and (ii), we get
C1 = 38.2 μF and C2= 11.8 μF
When the capacitors are connected in parallel, the charge on each of them can be obtained as follows :
Q1 = C1V = 38.2 × 10– 6 × 100
= 38.2 × 10- 4 C
Q2 = C2V = 11.8 × 10– 6 × 100
= 11.8 × 10– 4 C
![]()
Question 32.
(a) If two similar large plates, each of area A having surface charge densities + σ and- σ are separated by a distance in air, find the expressions for:
(i) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(ii) the potential difference between the plates.
(iii) the capacitance of the capacitor so formed.
(b) Two metallic spheres of radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, in which direction will the charge flow and why?
OR
(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
where \(\hat{n}\) is a unit vector normal to the surface at a point and a is the surface charge density at that point.
(The direction of \(\hat{n}\) is from side 1 to side 2). Hence show that just outside a conductor, the electric field is o \(\sigma \hat{n}_{/ \varepsilon_0}\).
(b) Show that the tangential component of electrostatic field is continuous from one side a charged surface to another.
[Hint: For (i) Use Gauss’ law. For (ii) use the fact that work done by electrostatic field on a closed loop is zero.]
Answer:
(a) (i) Consider a parallel plate capacitor with two identical plates X and Y, each having an area of A, and separated by a distance d. Let the space between the plates be filled by a dielectric medium with its dielectric constant as K and σ be the surface charge density on each of the plates.
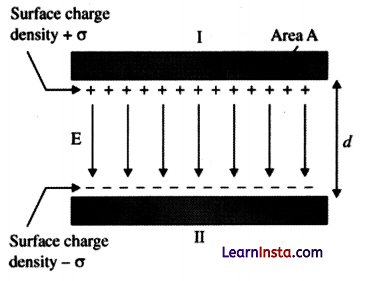
Surface charge density of plate 1
\(\sigma=\frac{Q}{A}\)and that of plate 2 is- σ.
Electric field in outer region I,
In the inner region between plates1 and 2, the electric fields due to the two charged plates add up.
So,
(ii) For uniform electric field, potential difference is simply the electric field multiplied by the distance between the plates, i.e.,
\(\mathrm{V}=\mathrm{E} d=\frac{1}{\varepsilon_0} \frac{\mathrm{Q} d}{\mathrm{~A}}\)(iii) Now, the capacitance of the parallel plate capacitor,
\(\mathrm{C}=\frac{\mathrm{Q}}{\mathrm{V}}=\frac{\mathrm{Q} \cdot \varepsilon_0 \mathrm{~A}}{\mathrm{Q} d}=\frac{\varepsilon_0 \mathrm{~A}}{d}\)(b) We know that the potential difference of the metallic sphere is given by,
\(\mathrm{V}=\frac{\mathrm{Q}}{4 \pi \varepsilon_0 r}\)
where r is the radius of the sphere.
Now, the potential of the metallic sphere of radius R is given by,
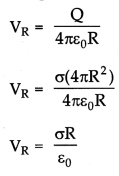
Similarly, the potential of the metallic sphere of radius 2R is given by

From the relation (i) and (ii) we know that V2R > VR.
The charge will flow from the sphere of radius of 2R to the sphere of radius R, if the spheres are connected.
OR
(a) Electric field on one side of a charged body is El and electric field on the other side of the same body is E2. If infinite plane charged body has a uniform thickness, then electric field due to one surface of the charged body is given by
\(\overrightarrow{\mathrm{E}}_1=-\frac{\sigma}{2 \varepsilon_0} \hat{n}\) ….(i)
where, \(\hat{n}\)= Unit vector normal to the surface at a point
σ = Surface charge density at that point
Electric field due to the other surface of the charged body,
\(\overrightarrow{\mathrm{E}_2}=\frac{\sigma}{2 \varepsilon_0} \hat{n}\) ….(ii)
Electric field at any point due to the two surfaces,

(b) When a charged particle is moved from one point to the other on a closed loop, the work done by the electrostatic field is zero. Hence, the tangential component of electrostatic field is continuous from one side of charged surface to the other.
![]()
Question 33.
(a) Draw a labelled ray diagram to obtain the real image formed by an astronomical telescope in normal adjustment position. Define its magnifying power.
(b) You are given three lenses of power 0.5 D, 4 D and 10 D to design a telescope.
(i) Which lenses should be used as objective and eyepiece? Justify your answer.
(ii) Why is the aperture of the objective preferred to be large?
OR
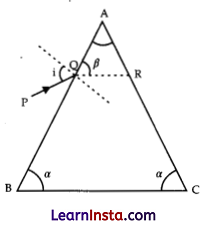
(a) A ray of light incident on the face AB of an isosceles triangular prism makes an angle of incidence (i) and deviates by angle β as shown in the figure.
Show that in the position of minimum deviation ∠β = ∠∝. Also find out the condition when the refracted ray QR suffers total internal reflection.
(b) Draw a labelled ray diagram of a refracting telescope. Defineits magnifying power and write the expression for it.
Write two important limitations of a refracting telescope over a reflecting-type telescope.
Answer:
(a)
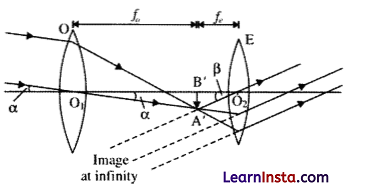
Magnifying power: The magnifying power of a refracting type astronomical telescope is defined as the ratio of angle subtended by the final image at eye to the angle subtended by the object at eye. We know that,
Magnification, m = \(\frac{f_o}{f_e}=\frac{\mathrm{P}_e}{\mathrm{P}_o}\)
(b) (i) The lens with the smallest power or largest focal length should be used as the objective i.e., lens with power 0.5 D.
(ii) The aperature is preferred to be large so that the telescope can collect as much as light coming from the distant object as possible.
OR
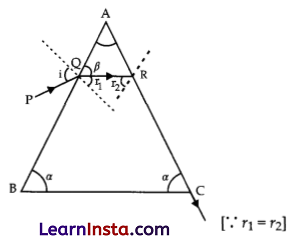
(a) \(\frac{\sin i}{\sin r}=\mu\)
Condition for minimum deviation:
1. A = 180-2∝
2. \(\frac{\sin i}{\sin (90-\beta)}=\mu\)
when,
r1= r2 = r> critical angle
r1 + r2= 180- 2∝
2r = 180-2∝
r = 90-∝
β = 90-r1
= 90- 90 + ∝
β = a
Condition when QR have total internal reflection:
∠QRC ≥ critical angle for the prism
∠180°- β ≥ critical angle
or ∠180°- ∝ ≥ critical angle
(b) Refracting telescope:
Magnifying power: The magnifying power is the ratio of the angle β subtended at the eye by the final image to the angle ∝ which the object subtends at the lens or the eye.
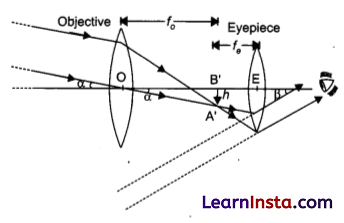
Limitations of refracting telescope over reflecting
type telescope :
(i) Refracting telescope suffers from chromatic aberration as it uses large sized lenses.
(ii) The requirement of big lenses tend to be very heavy and therefore, difficult to make and support by their edges.