CBSE Sample Papers for Class 12 Maths Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Set 2 with Solutions

Time Allowed: 3 hours
Maximum Marks: 70

General Instructions:

1. This question paper contains five sections – A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section – A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section – B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
4. Section – C has 6 Short Answer (SA)-type questions of 3 marks each.
5. Section – D has 4 Long Answer (LA)-type questions of 5 marks each.
6. Section – E has 3 source based/case based/passage based/integrated units of assessment (4 marks each) with sub parts.

Section – A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
If \(\left|\begin{array}{lll}2 & 3 & 2 \\x & x & x \\4 & 9 & 1\end{array}\right|\) + 3 = 0, then the value of x is :
(a) 3
(b) 0
(c) -1
(d) 1
Answer:
(c) -1
Explanation:
Given: \(\left|\begin{array}{lll}2 & 3 & 2 \\x & x & x \\4 & 9 & 1\end{array}\right|\) + 3 = 0
⇒ 2(x – 9x) -3 (x – 4x) + 2 (9x – 4x) + 3 = 0
⇒ -16x + 9x + 10x + 3 = 0
⇒ 3x = -3
⇒ x = -1.

Question 2.
If A and B are square matrices of the same order, then (A + B) (A – B) is equal to:
(a) A² – B²
(b) A² – BA – AB – B²
(C) A² – B² + BA – AB
(d) A² – BA + B² + AB
Answer:
(c) A² – B² + BA – AB
Explanation:
(A + B)(A – B) = A(A – B) + B(A – B)
= A² – AB + BA – B²

Question 3.
Find the continuity of f(x) = x at x = k, k be any positive value :
(a) f(x) is continuous at x = k
(b) f(x) is not continuous at x-k Sol.
(a) f(x) is continuous at x = k
(d) None of the above
Answer:
(a) f(x) is continuous at x = k
Explanation:
The given function is,
f(x) = x
At x = k,
f(k) = k
\(\lim _{x \rightarrow k} f(x)=\lim _{x \rightarrow k}(x)=k\)
\( \lim _{x \rightarrow k} f(x)=f(k)\)
∴ F(x) is continuous at x = k

Question 4.
The vector in the direction of the vector \( \hat{i}-2 \hat{j}+2 \hat{k}\) that has magnitude 9 is :
(a) \( \hat{i}-2 \hat{j}+2 \hat{k}\)
(b) \( \frac{\hat{i}-2 \hat{j}+2 \hat{k}}{3}\)
(c) \( 3(\hat{i}-2 \hat{j}+2 \hat{k})\)
(d) \(9(\hat{i}-2 \hat{j}+2 \hat{k})\)
Answer:
(c) \( 3(\hat{i}-2 \hat{j}+2 \hat{k})\)
Let \( \vec{a}=\hat{i}-2 \hat{j}+2 \hat{k}\)
Any vector in the direction of a vector [/latex]\vec{a}[/latex] is given by \(\frac{\vec{a}}{|\vec{a}|}\)
\( \frac{\hat{i}-2 \hat{j}+2 \hat{k}}{\sqrt{1^2+2^2+2^2}}\) = \(\frac{\hat{i}-2 \hat{j}+2 \hat{k}}{3}\)
∴ vector in the direction of with magnitude 9
= 9.\(\frac{\hat{i}-2 \hat{j}+2 \hat{k}}{3}\)
= \(3(\hat{i}-2 \hat{j}+2 \hat{k})\)

Question 5.
The degree of the differential equation \(\left(\frac{d^2 y}{d x^2}\right)^2+\left(\frac{d y}{dx}\right)^2[latex] = x sin [latex]\left(\frac{d y}{d x}\right)\) is:
(a) 1
(b) 2
(c) 3
(d) not defined
Answer:
(d) not defined
Explanation:
The degree of above differential equation is not defined because when we expand sin \(\left(\frac{d y}{d x}\right)\) we get an infinite series in increasing powers of \(\frac{d y}{d x}\) Therefore, its degree is not defined.

Question 6.
\(\int \frac{\cos 2 x-\cos 2 \theta}{\cos x-\cos \theta}\) dx is equal to:
(a) 2(sin x + x cos θ) + C
(b) 2(sin x + x cos θ) + C
(c) 2(sin x + 2x cos θ) + C
(d) 2(sin x – 2x cos θ) + C
Answer:
(a) 2(sin x + x cos θ) + C
Explanation:

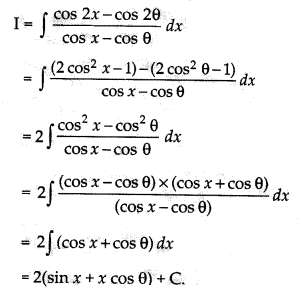
Question 7.
The vector having initial and terminal points as (2, 5, 0) and (-3, 7, 4), respectively is:
(a) \(-\hat{i}+12 \hat{j}+4 \hat{k}\)
(b) \(5 \hat{i}+2 \hat{j}-4 \hat{k}\)
(c) \(-5 \hat{i}+2 \hat{j}+4 \hat{k}\)
(d) \(\hat{i}+\hat{j}+\hat{k}\)
Answer:
(c) \(-5 \hat{i}+2 \hat{j}+4 \hat{k}\)
Explanation:
Required vector = \((-3-2) \hat{i}+(7-5) \hat{j}+(4-0) \hat{k}\)
= \(-5 \hat{i}+2 \hat{j}+4 \hat{k}\)

Question 8.
In an LPP, if the objective function z = ax + by has the same maximum value on two comer points of the feasible region, then the number of points at which zmax occurs is :
(a) 0
(c) finite
(b) 2
(d) infinite
Answer:
(d) infinite
Explanation:
Since, objective function has the same maximum value on two comer points, therefore every point on the segment joining these two points also given the maximum value. Hence, the number of points at which zmax occurs in infinite.

Question 9.
If A and B are symmetric matrices of the same order, then (AB’ – BA’) is a:
(a) Skew symmetric matrix
(c) Symmetric matrix
(b) Null matrix
(d) None of these
Answer:
(a) Skew symmetric matrix
Explanation:
Since, (AB’ – BA’)’ = (AB’)’ – (BA’)’
= (BA’ – AB’)
= – (AB’ – BA’).

Question 10.
\(\int \frac{x^3}{x+1}\) dx is equal to :
(a) \(x+\frac{x^2}{2}+\frac{x^3}{3}-\log |1-x|+\mathrm{C}\)
(b) \(x+\frac{x^2}{2}-\frac{x^3}{3}-\log |1-x|+\mathrm{C}\)
(c) \(x-\frac{x^2}{2}+\frac{x^3}{3}-\log |1+x|+\mathrm{C}\)
(d) \(x-\frac{x^2}{2}+\frac{x^3}{3}-\log |1+x|+\mathrm{C}\)
Answer:
(d) \(x-\frac{x^2}{2}+\frac{x^3}{3}-\log |1+x|+\mathrm{C}\)
Explanation:

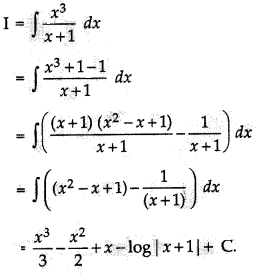
Question 11.
Let A = \(\left[\begin{array}{lr}200 & 50 \\ 10 & 2\end{array}\right]\) and B = \(\left[\begin{array}{ll}50 & 40 \\2 & 3\end{array}\right]\), then |AB| is equal to :
(a) 460
(b) 2000
(c) 3000
(d) -7000
Answer:
(d) -7000
Explanation:
|AB| = |A||B| = (400 – 500) (150 – 80)
= (-100) (70)
= -7000

Question 12.
Objective function is expressed in terms of the ………
(a) Numbers
(b) Symbols
(c) Decision variables
(d) None of these
Answer:
(c) Decision variables
Explanation:
As it involves decision variables, for which function need to maximised or minimised.

Question 13.
From the set {1,2,3,4,5}, two numbers a and b(a ≠ b) are chosen at random. The probability that \(\frac{a}{b}\) is an integer is:
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{5}\)
Answer:
(b) \(\frac{1}{4}\)
Explanation:
Total possible outcomes of (a, b) = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 3), (2, 4), (2, 5), (3,1), (3, 2), (3, 4), (3, 5), (4,1), (4, 2), (4, 3), (4, 5), (5,1), (5, 2), (5, 3), (5,4)}
⇒ Number of possible outcomes = 20
Also, favourable outcomes of (a, b) = {(2,1), (3,1), (4,1), (4, 2), (5,1)}
⇒ Number of possible outcomes = 5
\(\mathrm{P}\left(\frac{a}{b} \text { is an integer }\right)=\frac{5}{20}=\frac{1}{4}\)

Question 14.
If \(\left|\begin{array}{cc}x & 2 \\18 & x\end{array}\right|=\left|\begin{array}{cc}6 & 2 \\18 & 6\end{array}\right|\), then the value of x is :
(a) ±2
(b) 0
(c) ±3
(d) ±6
Answer:
(d) ±6
Explanation:
\(\left|\begin{array}{cc}x & 2 \\18 & x\end{array}\right|=\left|\begin{array}{cc}6 & 2 \\18 & 6\end{array}\right|\)
⇒ x² – 36 = 36 – 36
⇒ x² – 36 = 0 ⇒ x – ±6

Question 15.
Find the continuity of f(x) = \(\frac{x^2-16}{x+4}\), x ≠ – 4 at x = k, k be any positive value:
(a) f(x) is not containuous at x = k
(b) f(x) is containuous at x = k
(c) f(x) is containuous at x = -4
(d) f(x) isnot containuous at x = -4
Answer:
(b) f(x) is containuous at x = k
Explanation:
The given function is, f(x) = \(\frac{x^2-16}{x+4}\)
At x = K,

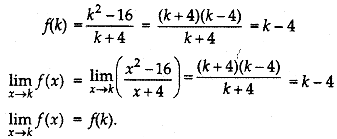
∴ f(x)is contains at x = k

Question 16.
The degree of the differential equation \(\left[1+\left(\frac{d y}{d x}\right)^2\right]^{3 / 2}=\frac{d^2 y}{d x^2}\) is:
(a) 4
(b) \(\frac{3}{2}\)
(c) not defined
(d) 2
Answer:
(d) 2
Explanation:
Given that,
\(\left[1+\left(\frac{d y}{d x}\right)^2\right]^{3 / 2}=\frac{d^2 y}{d x^2}\)
On squaring both sides, we get
\(\left[1+\left(\frac{d y}{d x}\right)^2\right]^3=\left(\frac{d^2 y}{d x^2}\right)^2\)
So, the degree of differential equation is 2.

Question 17.
The differential coefficient of sin (cos (x²)) with respect to x is :
(a) -2x sin x² cos (cos x²)
(b) 2x sin (x²) cos (x²)
(c) 2x sin (x²) cos (x²) cos x
(d) None of the above
Answer:
We have, y = sin (cos(x²))
Therefore, \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)sin (cos x²)
= cos(cos x²)\(\frac{d y}{d x}\)(cos x²)
= cos(cos x²)(-sin x²)\(\frac{d y}{d x}\)(x²)
= -sin x² cos(cos x²)(2x)
= -2x sin x² cos(cos x²)

Question 18.
The area of the region bounded by the curve x = 2y + 3 and the lines y = 1, y = – 1 is :.
(a) 4 sq. units
(b) \(\frac{3}{2}\)
(c) 6 sq. units
(d) 8 sq. units
Answer:
(c) 6 sq. units
Explanation: Required area,

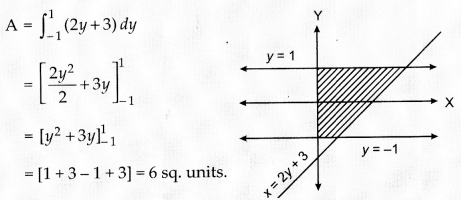
Question 19.
Assertion (A): In a ∆ABC, \(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}\) = 0
Reason (R): If \(\overrightarrow{\mathrm{AB}}=\vec{a} \cdot \overrightarrow{\mathrm{BC}}=\vec{b}\)
then \(\overrightarrow{\mathrm{AC}}=\vec{a}+\vec{b}\)(Triangle law of addition).
Answer:
(a) Both A and B are true and R is the correct explanation of A.
Explanation:
\(\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}\) = \(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CA}}\)
= \(\overrightarrow{A C}-\overrightarrow{A C}\)
= 0.

Question 20.
Assertion (A): sin^-1 (sin 3) = 3
Reason (R): For principal value sin^-1 (sin x) = x
Answer:
(d) A is false but R is true.
Explanation:
3 ≈ 171° (lies in II question)
∴ sin^-1sin 3 = 3 – π ≠ x
But sin^-1sin x = x for principal values.

Section – B
[This section comprises of very short answer type questions (VSA) of 2 marks each]

Question 21.
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 3x² + 36x + 5. Find the marginal revenue, when x = 5, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant.
OR
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x³ – 0.02x² + 30x + 5000. Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Answer:
Since the marginal revenue is the rate of change of total revenue with respect to the number of units sold, we have
R(x) = 3x² + 36x + 5
On differentiating with respect to x, we get Marginal Revenue
(MR) = \(\frac{d \mathrm{R}}{d x}\) = 6x + 36
When x = 5, MR = 6(5) + 36 = 66
Hence, the required marginal revenue is ₹66.
Or
Cost function is given as
C(x) = 0.005x³ – 0.02x² + 30x + 5000
Marginal cost = \(\left[\frac{d}{d x}(\mathrm{C}(x))\right]_{x=3}\)
= [0.015x² – 0.04x + 30]_x=3
= 0.015(3)² – 0.04(3) + 30
= 0.135 – 0.12 + 30
= 30.015.

Question 22.
If R = {(x, y): x + 2y = 8} is a relation on N, then the range of R is …… .
Answer:
{1,2,3}
The given relation on N is
R = {(x, y): x + 2y = 8}
Since both x, y e N,
x can take value 2, 4, 6, for all x, y ∈ N.
For x = 2, 2 + 2y = 8
⇒ y = 3
For x = 4, 4 + 2y = 8
⇒ y = 2
For x = 6, 6 + 2y = 8
⇒ y = 1
R = {(2, 3), (4, 2), (6,1)}
The range of R = Set of second elements
= {1, 2, 3}.

Question 23.
The solution of differential equation \(\frac{d y}{d x}\) = x³ + e^x + x^e is ……. .
Or
The solution of the differential equation (e^x + e^-x) dy = (e^x – e^-xdx is ….. .
y = \(\frac{x^4}{4}+e^x+\frac{x^{e+1}}{e+1}\) + C
Given differential equation is
\(\frac{d y}{d x}\) = x³ + e^x + x^e
On integrated both sides, we get y = \(\int x^3 d x+\int e^x d x+\int x^e d x+\mathrm{C}\)
= \(\frac{x^4}{4}+e^x+\frac{x^{e+1}}{e+1}\)+ C
Or
Y = log |e^x + e^-x| + C
Given differential equation is
(e^x + e^-x dy = (e^x – e^-x)dx
⇒ dy = \(\frac{\left(e^x-e^{-x}\right)}{\left(e^x+e^{-x}\right)}\) dx
On integrated both sides, we get
y = \(\int \frac{\left(e^x-e^{-x}\right)}{\left(e^x+e^{-x}\right)}\)dx
Let e^x + e^-x = t
(e^x – e^-x)dx = dt
y = \(\int \frac{1}{t}\) = log t + C
= Log |e^x + e^-x| + C.

Question 24.
The direction cosines of a line are proportional to 2, -3, 6. Find the actual values of the direction cosines.
Answer:
If l,m,n are the direction cosines of the line then
l : m : n = : -3 : 6

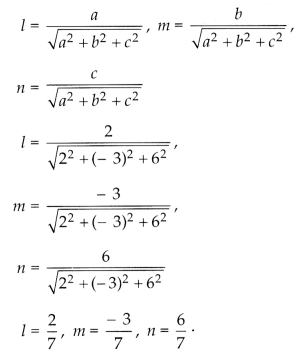
Question 25.
Determine the value of T for which the following function is continuous at x = 3.

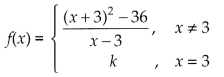
Answer:

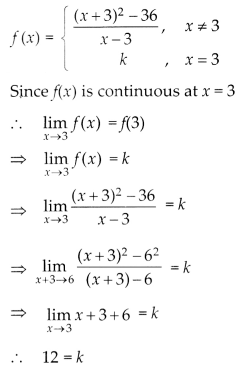
Thus,f(x) is continuous at x = 3, if k = 12.

Section – C
[This section comprises of short answer type questions (SA) of 3 marks each]

Question 26.
Evaluate P(A u B), if 2P(A) = P(B) = \(\frac{5}{13}\) and P(A/B) = \(\frac{2}{5}\)
Answer:
Given 2p(A) = \(\frac{5}{13}\)
⇒ P(A) = \(\frac{5}{26}\) and p(B) = \(\frac{5}{13}\)
Also, P(A/B) = \(\frac{2}{5}\)
We know that

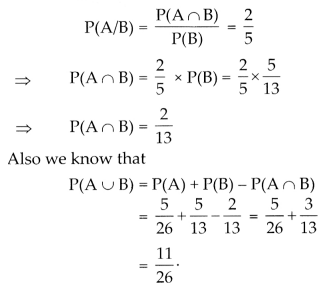
Question 27.
Solve the following L.P.P. graphically : Maximize Z = 4x + y Subject to following constraints
x + y ≤ 50,
3x + y ≤ 90,
x ≥ 10
x,y ≥ 0
Answer:
x + y = 50

x	0	50
y	50	0

3x + y = 90

x	0	30
y	90	0

x = 10 is a line which is paraller to y – axis.

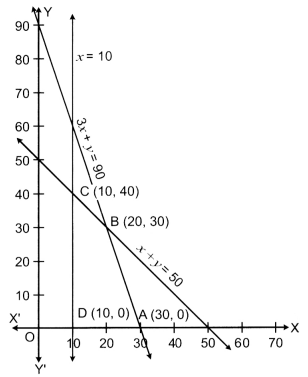
Corner points	Z = 4x + y
A(30,0)	Z = 120 + 0 = 120 ← Maximum
B(20,30)	Z = 80 + 30 = 110
C(10,40)	Z = 40 + 40 = 80
D(10,0)	Z = 40 + 0 = 40

∴ Maximum value is 120 at (30,0).

Question 28.
Find the particular solution of the differential equation satisfying the given condition.
\(\frac{d y}{d x}\) = y tan x, given that y = 1 when x = 0.
Or
Solve the following differential equation :
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x
Answer:
Given Differential equation is
\(\frac{d y}{d x}\) = y tan x
⇒ \(\frac{d y}{y}\) = tan x dx
On integrating both sides, we get,
log y = log |sex x| + log C
⇒ log y = log |C sex x|
⇒ y = C sec x
When y = C sex x
Equation (ii)becomes 1 = C sec 0
C = 1
Put it in equation (ii)
y = sec x is required solution
Or
Given differential equation is
(x³ + x² + x + 1) \(\frac{d y}{d x}\) = 2x² + x
dy = \(\frac{\left(2 x^2+x\right)}{x^3+x^2+x+1} d x\)
On increasing both sides, we get
Img-1
⇒ 2x² + x = A (x² + 1) + (Bx + C) + (x + 1)
⇒ 2x² + x = Ax² + A + Bx + Cx + C
2x² + x = x² (A + B) + x(B + C) + A + C
When x = 1
3 = 2A + 2B + 2C
⇒ 3 = 2 × \(\frac{1}{2}\) + 2B + 2\(\left(-\frac{1}{2}\right)\)
⇒ 3 = 1 + 2B – 1
⇒ 2B = 3
⇒ B = \(\frac{3}{2}\)
From equation (i),

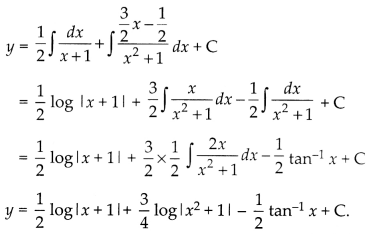
is the required solution.

Question 29.
Find ∫cos 2x cos 4x cos 6x dx
Or
Evaluate \(\int \frac{1}{\cos (x-a) \cos (x-b)} d x\)
Answer:

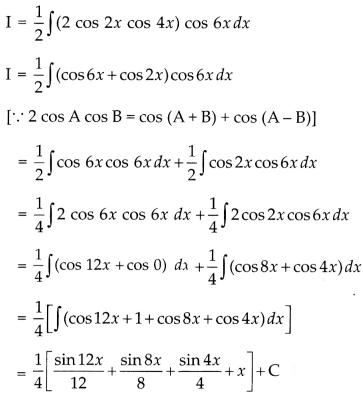
Or
Let \(\int \frac{1}{\cos (x-a) \cos (x-b)} d x\)

Question 30.
Evaluate \(\int \frac{e^x}{\sqrt{5-4 e^x-e^{2 x}}}\)dx
Or
Find \(\int \frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}\)dx
Answer:

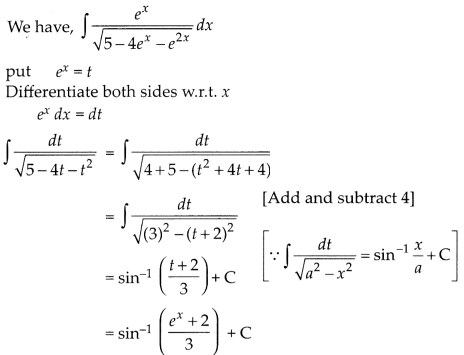
Or
Let \(\int \frac{e^{2 x}-e^{-2 x}}{e^{2 x}+e^{-2 x}}\)dx

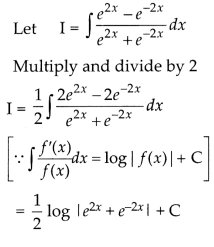
Question 31.
Find ∫\(\frac{1}{sec x + cosc x}\)dx
Answer:

Section – D
[This section comprises of long answer type questions (LA) of 5 marks each]

Question 32.
Show that the relation R defined on the set A of all polygons as R = {(Pa, P2): P, and P2 have same number of sides) is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5 ?
Answer:
Given, R = {(P₁, P₂): P₁ and P₂ have same number of sides}
Reflexivity : Let P be any polygon in A.
Then, P and P have same number of sides.
⇒ (P,P) ∈ R
Thus, (P,P) ∈ R, ∀ P ∈ A
So, R is reflexive.

Symmetric :
Let P₁ and P₂ be two polygons in A such that
(P₁,P₂) ∈ R
Now, P₁ and P₂ have same number of sides.
⇒ P₂– P₁ have same number of sides.
⇒ (P₂,P₁) ∈ R
So, R is symmetric on A.

Transitivity :
Let P₁, P₂ and P₃ be three polygons in A such that (P₁, P₂) ∈ R and (P₂, P₃) ∈ R.
Then,(P₁, P₂) ∈ R ⇒ P₁, and P₂ have same number of sides.
and (P₂,P₃) ∈ R ⇒ P₂ and P₃ have same number of sides.
∴ P₁ and P₃ have same number of sides.
⇒ (P₁, P₃) ∈ R
Thus, if (P₁, P₂) ∈ R and P₂, (P₃) ∈ R
⇒ (P₁, P₃) ∈ R
So, R is transitive.
Hence, R is an equivalence relation on A.
Let P be a polygon in A such that (P, T) e R. Then, polygon P and triangle T have same number of sides. Thus, P is any triangle in A with sides 3, 4 and 5.

Question 33.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, X-axis and the lines x = 2 and x = 8.
OR
Find the area of the region included between y² = 9x and y = x.
Answer:
We have,
2y = 5x + 7
⇒ y = \(\frac{5 x}{2}+\frac{7}{2}\)

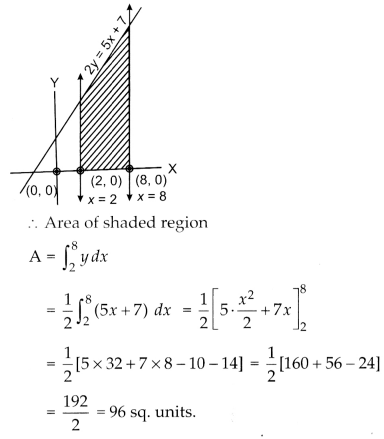
Or
We have, x² = 9x and y = x
⇒ x² = 9x
⇒ x² – 9x = 0
⇒ x(x – 9) = 0
x = 0,9
∴ Area of shaded region

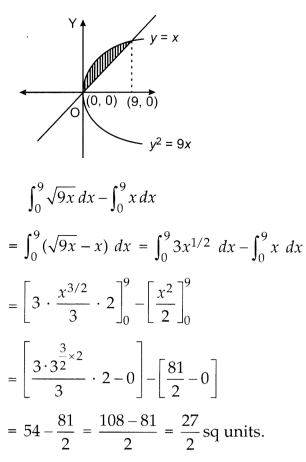
Question 34.
Find the vector and Cartesian equation of line passing through point (1, 2, – 4) and perpendicular to two
line \(\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}\) and \(\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\)
Answer:
Let the required equation of line passing through (1, 2, – 4) is
\(\frac{x-1}{a}=\frac{y-2}{b}=\frac{z+4}{c}\) …….(i)
Given that line (i) is perpendicular to lines

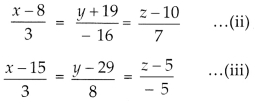
We know that when two lines are perpendicular then we have a₁a₂ + b₁b₂ + c₁c₂ = 0, where a₁, b₁, c₁ and a₂, b₂, c₂ are the direction ratios of two lines. Using this property first in equations (i) and (ii) and then in equations (i) and (iii), we get
3a – 16b + 7c = 0 …….(iv)
(∵ a₁a₂ + b₁b₂ + c₁c₂ = 0
and 3a + 8b – 5c = 0
Subtracting equation (v) from equation (iv), we get

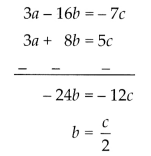
Putting b = \(\frac{c}{2}\) in equation (iv), we get
3a – 16\(\left(\frac{c}{2}\right)\) + 7c = 0
⇒ 3a – 8c + 7c = 0
⇒ 3a – c = 0
⇒ a = \(\left(\frac{c}{3}\right)\)
Putting a = \(\left(\frac{c}{3}\right)\) and b = \(\left(\frac{c}{2}\right)\) in equation (i), we get the required equation ofline as

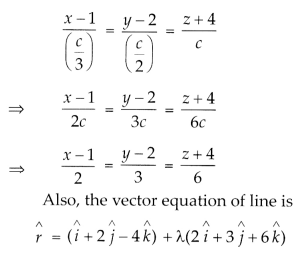
Question 35.
If A = \(\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\-\sin \alpha & \cos \alpha\end{array}\right]\) verify that AA’ = A’A = I.
OR
Find matrix A such that \(\left[\begin{array}{rr}2 & -1 \\1 & 0 \\-3 & 4\end{array}\right]\) A = \(\left[\begin{array}{rr}-1 & -8 \\1 & -2 \\9 & 22\end{array}\right]\)
Answer:

Or

By equation of matrices, on comparing we get
2a – c = -1
2b – d = -8
also, a = 1
b = -2
and -3a + 4c = 9
-3b + 4d = 22
on solving the equation, we get
a = 1, b = -2, c = 3, d = 4
Hence, A = \(\left[\begin{array}{rr}1 & -2 \\3 & 4\end{array}\right]\)

Section – E
[This section comprises of 3 case-study/passage-based questions of 4 marks each with sub-parts. The First two case study questions have three sub-parts (i), (ii), (iii) of marks 1,1, 2 respectively. The third case
study question has two sub parts of 2 marks each]

Question 36.
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as show below :

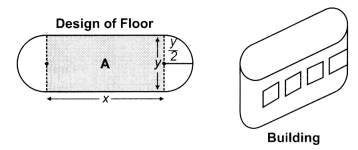
Based on the above information answer the following :
(i) If x and y represents the length and breadth of the rectangular region, then find the relation between the variables.
(ii) Find the area of the rectangular region A expressed as a function of x.
(iii) Find the maximum value of area A.
OR
(iii) The CEO of the multi-national company is interested in maximising the area of the whole floor including the semi-circular ends. For this to happen the value of x should be.
Answer:
(i)Perimeter = 200 m
⇒ 2x + 2π\(\left(\frac{y}{2}\right)\) = 200
⇒ 2x + πy = 200

(ii) Area of rectangular region = L × B
⇒ A = xy = x\(\left(\frac{200-2 x}{\pi}\right)\)
∴ A = \(\frac{2}{\pi}\)(100x – x²)

(iii) \(\frac{d \mathrm{~A}}{d x}\) = \(\frac{2}{\pi}\)(100 – 2x)
Put \(\frac{d \mathrm{~A}}{d x}\) = 0 ⇒ x = 50
\(\frac{d^2 \mathrm{~A}}{d x^2}\) = \(\frac{2}{\pi}\)(-2) < 0
∴ A is maximum when
x = 50
∴ Maximum area = \(\frac{2}{\pi}\)(5000 – 2500) = \(\frac{5000}{\pi}\) m²
Or
(iii) Area of whole floor = xy + π\(\left(\frac{y}{2}\right)^2\)

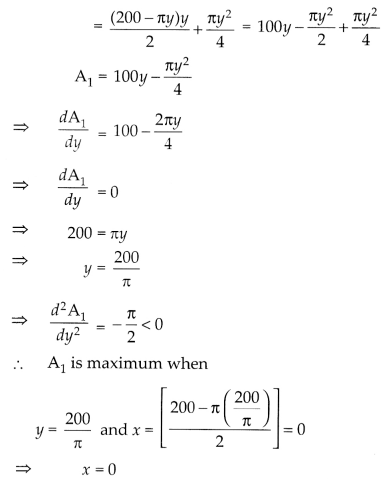
Question 37.
In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Based on the above information answer the following :
(i) Find the conditional probability that an error is committed in processing given that Sonia processed the form.
(ii) Find the probability that Sonia processed the form and committed an error.
(iii) Find the total probability of committing an error in processing the form.
OR
(iii) The manager of the company wants to do a quality check. During inspection he selects a form at random from the days output of processed forms. If the form selected at random has an error. Find the probability that the form is not processed by Vinav.
Answer:

Question 38.
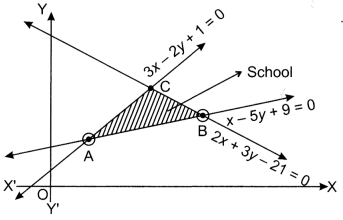
A school is to be constructed for the rural area children on the wasted land which is lying under the area covered by the lines 3x – 2y + 1 = 0, 2x + 3y – 21 = 0 and x – 5y + 9 = 0.