CBSE Sample Papers for Class 12 Maths Paper 3 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 3.
CBSE Sample Papers for Class 12 Maths Paper 3
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 3 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 3 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
State the reason why the Relation R = {(a, b) : a ≤ b2} on the set R of real numbers is not reflexive.
Question 2.
If A is a square matrix of order 3 and |2A| = k |A|. then find the value of k.
Question 3.
If \(\vec { a }\) and \(\vec { b }\) are two non-zero vectors such that \(\left| \vec { a } \times \vec { b } \right| =\vec { a } \cdot \vec { b }\), then find the angle between \(\vec { a }\) and \(\vec { b }\).
Question 4.
If * is a binary operation on the set R of real numbers defined by a * b = a + b – 2, then find the identity element for the binary operation *.
SECTION B
Question 5.
Simplify \({ cot }^{ -1 }\frac { 1 }{ \sqrt { { x }^{ 2 }-1 } }\) for x < -1.
Question 6.
If A and B are symmetric matrix then prove that AB – BA is skew symmetric.
Question 7.
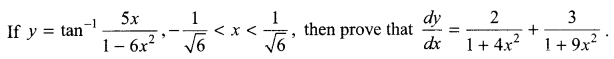
Question 8.
If x changes from 4 to 4.01, then find the approximate change in loge x.
Question 9.
Find \(\int { \left( \frac { 1-x }{ 1+{ x }^{ 2 } } \right) ^{ 2 } } { e }^{ x }dx\)
Question 10.
Obtain the differential equation of the family of circles passing through the points (a, 0) and (-a, 0).
Question 11.
![]()
Question 12.
![]()
SECTION C
Question 13.
If \(A=\begin{pmatrix} 1 & -2 \\ 2 & 1 \end{pmatrix}\), then using A-1 solve the following system of equations: x – 2y = -1, 2x + y = 2.
Question 14.

Question 15.
If x = a sin pt, y = b cos pt, then show that \(\left( { a }^{ 2 }-{ x }^{ 2 } \right) y\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } +{ b }^{ 2 }=0\)
Question 16.
Find the equation of the normal to the curve 2y = x2, which passes through the point (2, 1).
OR
Separate the interval [0, \(\frac { \pi }{ 2 }\)] into subintervals in which the function f(x) = sin4x + cos4x is strictly increasing or strictly decreasing.
Question 17.
A magazine seller has 500 subscribers and collects annual subscription charges of ₹ 300 per subscriber. She proposes to increase the annual subscription charges and it is believed that for every increase of ₹ 1, one subscriber will discontinue. What increase will bring maximum income to her? Make appropriate assumptions in order to apply derivatives to reach the solution. Write one important role of magazines in our lives.
Question 18.
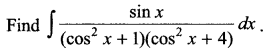
Question 19.
Find the general solution of the differential equation (1 + tan y) (dx – dy) + 2xdy = 0.
OR
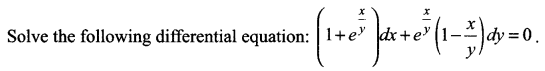
Question 20.
![]()
Question 21.
Find the values of‘a’so that the following lines are skew:
![]()
Question 22.
A bag contains 4 green and 6 white balls. Two balls are drawn one by one without replacement. If the second ball drawn is white, what is the probability that the first ball drawn is also white?
Question 23.
Two cards are drawn successively with replacement from a well shuffled pack of 52 cards. Find the probability distribution of the number of diamond cards drawn. Also, find the mean and the variance of the distribution.
SECTION D
Question 24.
Let f: [0, ∞) → R be a function defined by fx) = 9x2 + 6x – 5. Prove that f is not invertible. Modify, only the codomain of f to make f invertible and then find its inverse.
OR
Let * be a binary operation defined on Q x Q by (a, b) * (c, d) = (ac, b + ad), where Q is the set of rational numbers. Determine, whether * is commutative and associative. Find the identity element for * and the invertible elements of Q x Q.
Question 25.
Using properties of determinants, prove that
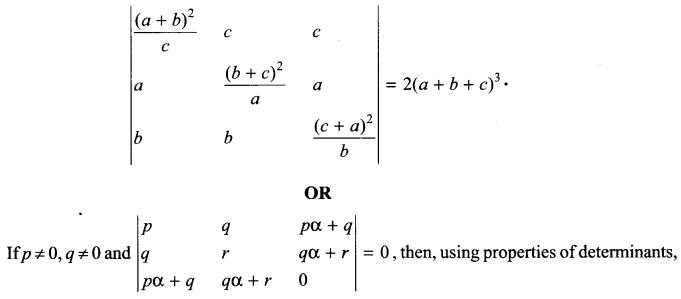
prove that atleast one of the following statements is true:
(a) p, q, r are in G.P.
(b) a is a root of the equation px2 + 2qx + r = 0.
Question 26.
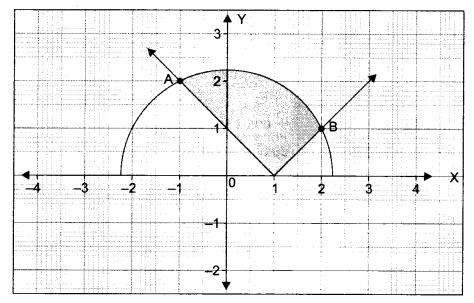
Using integration, find the area of the region bounded by the curves y = √(5 – x2) and y = |x – 1|.
Question 27.
Evaluate the following:
\(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { xsinx\quad cosx }{ { sin }^{ 4 }x+{ cos }^{ 4 }x } } dx\)
OR
Evaluate \(\int _{ 0 }^{ 4 }{ \left( x+{ e }^{ 2x } \right) } dx\)
Question 28.
Find the equation of the plane through the point (4, -3, 2) and perpendicular to the line of intersection of the planes x – y + 2z – 3 = 0 and 2x – y – 3z = 0. Find the point of intersection of the line \(\vec { r } =\vec { i } +2\vec { j } -\vec { k } +\lambda \left( \vec { j } +3\vec { j } -9\vec { k } \right)\) and the plane obtained above.
Question 29.
In a mid-day meal programme, an NGO wants to provide vitamin rich diet to the students of an MCD school. The dietician of the NGO wishes to mix two types of food in such a way that vitamin contents of the mixture contains atleast 8 units of vitamin A and 10 units of vitamin C. Food 1 contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C. Food 2 contains 1 unit per Kg of vitamin A and 2 units per kg of vitamin C. It costs ₹ 50 per kg to purchase Food 1 and ₹ 70 per kg to purchase Food 2. Formulate the problem as LPP and solve it graphically for the minimum cost of such a mixture?
Solutions
Solution 1.
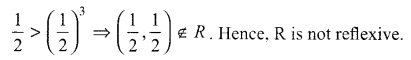
Solution 2.
k = 23 = 8
Solution 3.
sin θ = cos θ ⇒ θ = 45°
Solution 4.
e ∈ R is the identity element for * if a * e = e * a = a ∀ a ∈ R ⇒ a + e – 2 = a ⇒ e = 2
Solution 5.
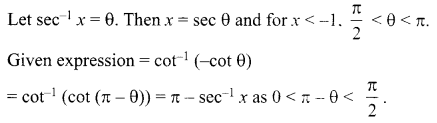
Solution 6.
A, B is symmetric matrix so A’ = A, B’ = B
(AB – BA)’ = (AB)’ – (BA)’ = B’A’ – A’B’ = BA – AB = – (AB – BA)
So AB – BA is skew symmetric matrix.
Solution 7.
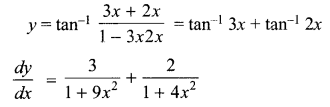
Solution 8.
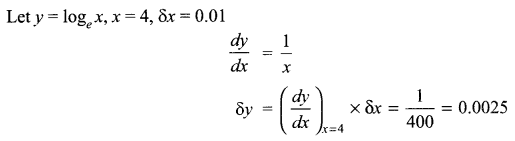
Solution 9.
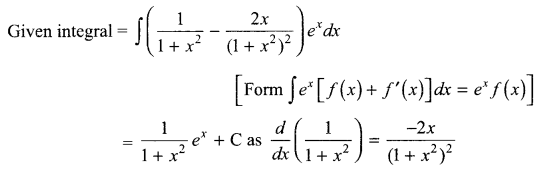
Solution 10.
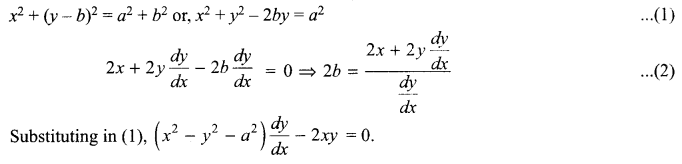
Solution 11.
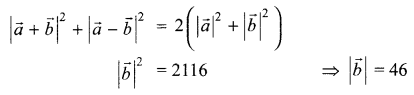
Solution 12.
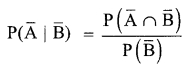
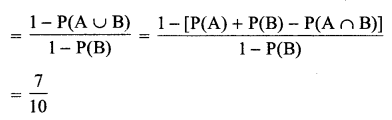
Solution 13.
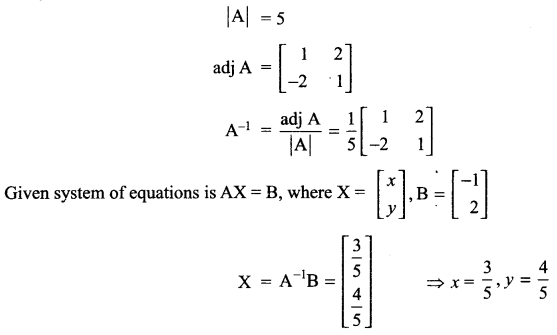
Solution 14.
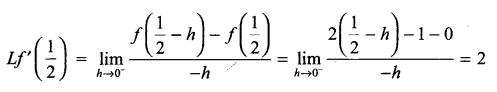
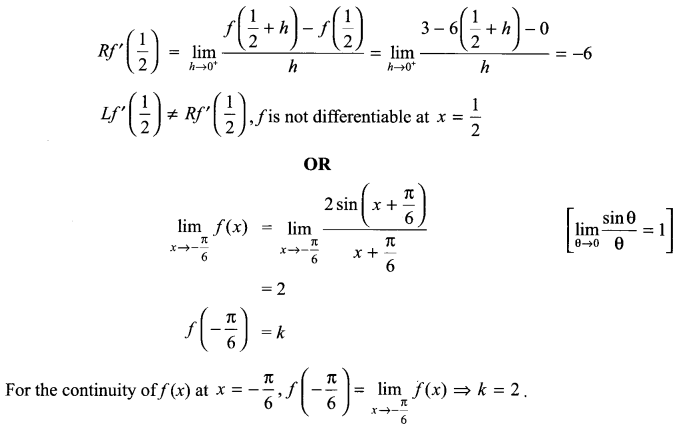
Solution 15.
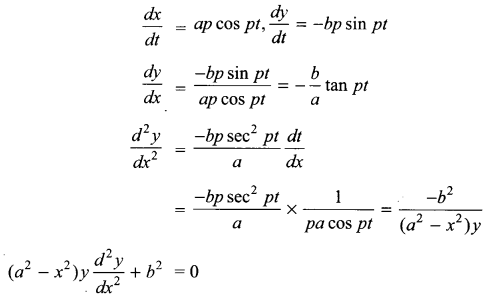
Solution 16.
Let the normal be at (x1, y1) to the curve 2y = x2. \(\frac { dy }{ dx }\) = x.
The slope of the normal at

Solution 17.
Increase in subscription charges = ₹ x, Decrease in the number of subscriber = x.
Obviously, x is a whole number.
Income is given by y = (500 – x) (300 + x).
Let us assume for the time being
0 ≤ x < 500, x ∈ R
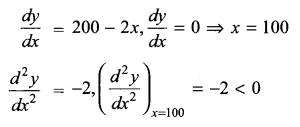
y is maximum when x = 100, which is a whole number. Therefore, she must increase the subscription charges by ₹ 100 to have maximum income.
Magazines contribute, a great deal, to the development of our knowledge. Through valuable and subtle critical and commentary articles on culture, social civilization, new life style we learn a lot of interesting things. Through reading magazines, our mind and point of view are consolidated and enriched.
Solution 18.
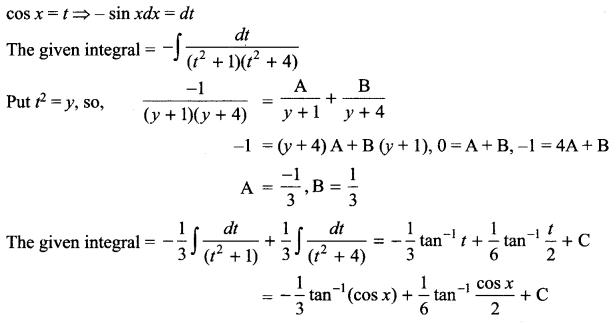
Solution 19.
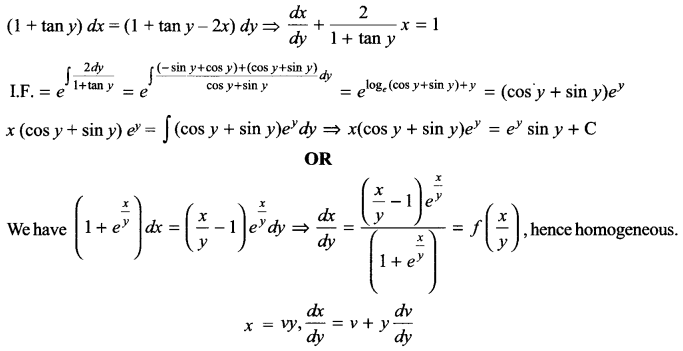
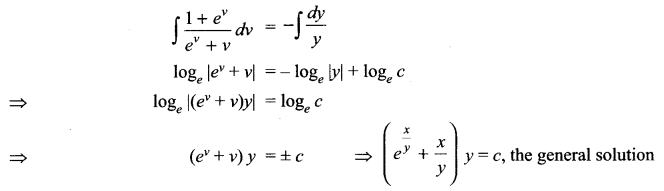
Solution 20.
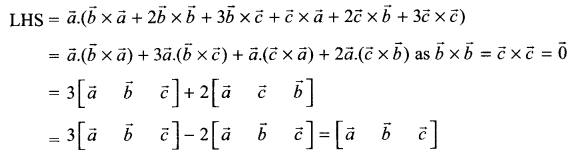
Solution 21.
As 2 : 3 : 4 ≠ 5 : 2 : 1, the lines are not parallel
Any point on the first line is (2λ + 1, 3λ + 2, 4λ + a)
Any point on the second line is (5μ + 4, 2μ + 1, μ)
Lines will be skew, if, apart from being non-parallel, they do not intersect. There must not exist a pair of values of λ, μ, which satisfy the three equations simultaneously:
2λ + 1 = 5μ + 4, 3λ + 2 = 2μ + 1, 4λ + a = μ
Solving the first two equations, we get λ = -1, μ = -1
These values will not satisfy the third equation if a ≠ 3
Solution 22.
Let E1 = First ball drawn is white,
E2 = First ball drawn is green,
A = Second ball drawn is white
The required probability, by Bayes’ Theorem
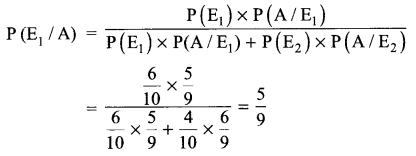
Solution 23.

Solution 24.
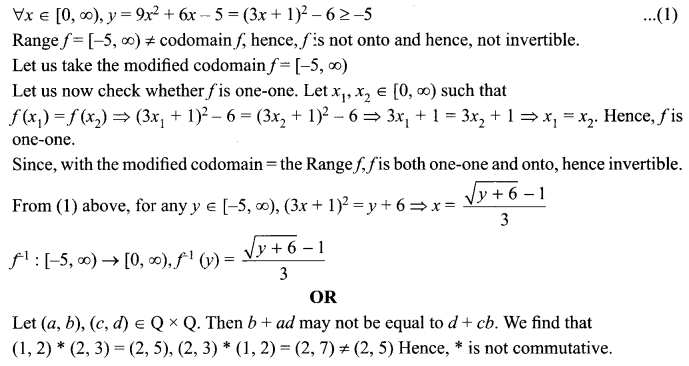

Solution 25.
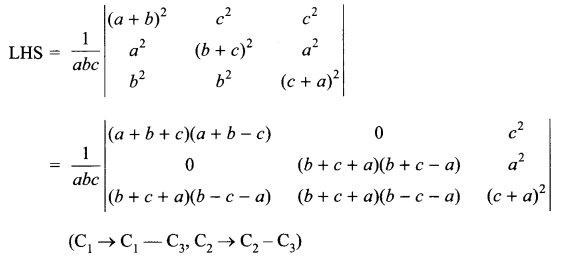
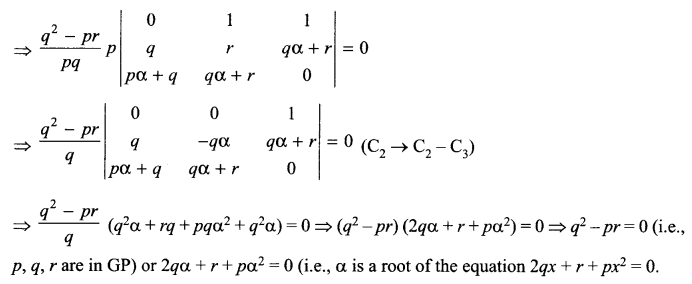
Solution 26.
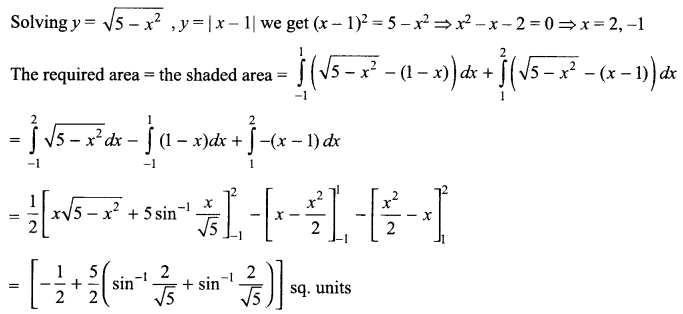
Solution 27.
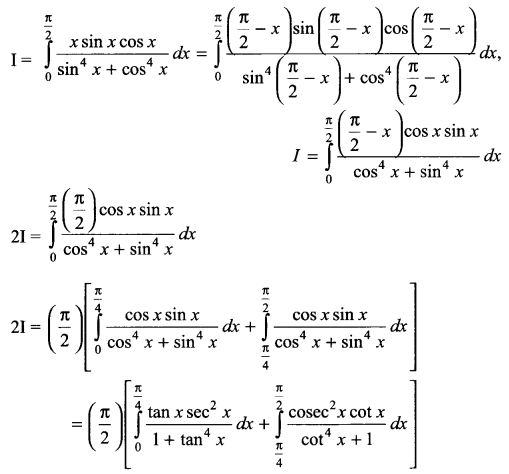
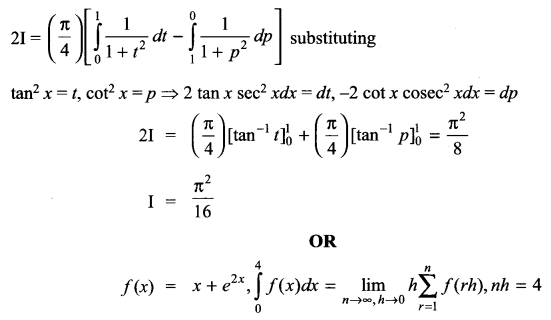

Solution 28.
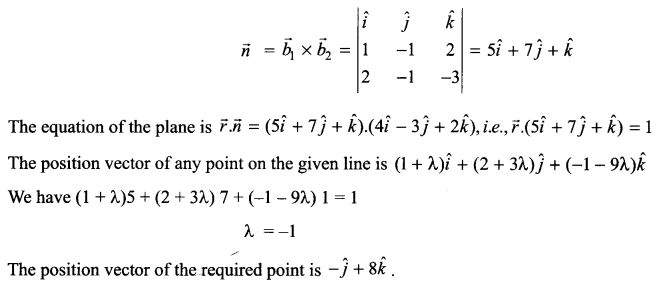
Solution 29.
Let x kg of Food 1 be mixed with y kg of Food 2. Then to minimize the cost, C = 50x + 70y subject to the following constraints:
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0
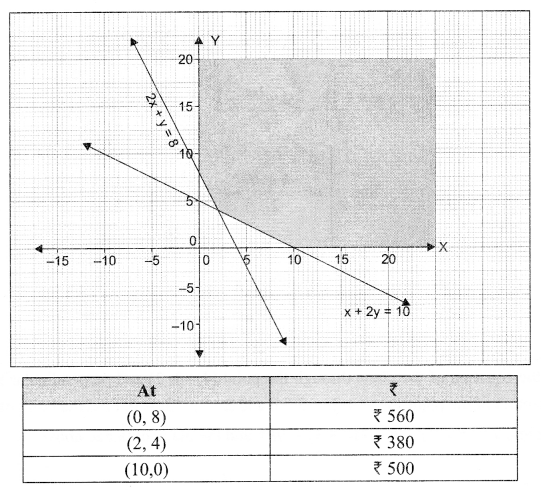
In the half plane 50x + 70y < 380, there is no point common with the feasible region. Hence, the minimum cost is ₹ 380.
We hope the CBSE Sample Papers for Class 12 Maths Paper 3 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 3, drop a comment below and we will get back to you at the earliest.