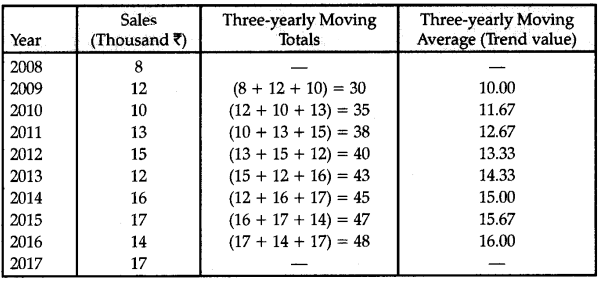CBSE Sample Papers for Class 12 Applied Maths Set 8 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Maths with Solutions and marking scheme Set 8 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Maths Set 8 with Solutions

Time Allowed : 3 hours
Maximum Marks : 80

General Instructions:

1. This Question paper contains – five sections A,B,C,D and E. Each section is compulsory. However, there is some internal ‘ choice in some questions.
2. Section A has 18 MCQ’s and 02 Assertion Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
4. Section C has 6 Short Answer (SA) questions of 3 marks each.
5. Section D has 4 Long Answer (LA) questions of 5 marks each.
6. Section E has 3 source based/case based/passage based/integrated units of assessment (04 marks each) with sub parts.
7. Internal Choice is provided in 2 questions in Section-B, 2 questions in Section-C, 2 Questions in Section-D. You have to attempt only one alternatives in all such questions.

Section – A
(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
If a = b (mod m), then
(A) a (mod m) = b(mod m)
(B) a (mod a) = b (mod m)
(C) a ≡ a (mod m)
(D) None of these
Answer:
(A) a (mod m) = b(mod m)

Question 2.
If \(\frac{|x+1|}{x+1}\) > 0 x ∈ R then
(A) x ∈ (- 1, ∞)
(B) x ∈ (- 1, ∞)
(C) x ∈ (- ∞, 1)
(D) x ∈ (- ∞, – 1)
Answer:
(B) x ∈ (- 1, ∞)

Explanation:
If \(\frac{|x+1|}{x+1}\) > 0 then to make the given fraction, greater than zero denominator should always be greater than zero.
So, x + 1 > 0 = x > \- 1
or, x ∈ (- 1, ∞)

Question 3.
Which of the following is a branch of statistics?
(A) Descriptive Statistics
(B) Lnferential Statistics
(C) Industrial Statistics
(D) Both A and B
Answer:
(D) Both A and B

Explanation:
Study of statistics can be categorized in two types:
(i) Descriptive Statistics
(ii) Inferential Statistics.

Question 4.
A sample of 50 pens is taken at random. out of 50 pens we found 15 pens are of Cello, 17 are of Parker and 18 are of Reynolds. What is the point estimate of population proportion of Parker.
(A) 0.3
(B) 0.34
(C) 0.36
(D) 0.4
Answer:
(B) 0.34

Explanation:
Popular proportion of Parker
\(\frac{17}{50}\) = 0.34

Question 5.
If a man rows 32 km downstream and 14 km upstream in 6 hours each, then the speed of the stream is
(A) 2 km/h
(B) 1.5 km/h
(C) 2.5 km/h
(D) 2.25 km/h
Answer:
(B) 1.5 km/h

Explanation:
Upstream speed = \(\frac{14}{6}\) km/h
Downstream speed = \(\frac{32}{6}\) km/h
Speed of the stream = \(\frac{\frac{32}{6}-\frac{14}{6}}{2}=\frac{\frac{18}{6}}{2}\)
= \(\frac{18}{6 \times 2}=\frac{3}{2}\)
= 1.5 km/h

Question 6.
A candidate claims 70% of the people in her constituency would vote for her. If 120000 valid votes are polled, then the number of votes she expects from her constituency is
(A) 100000
(B) 84000
(C) 56000
(D) 36000
Answer:
(B) 84000

Explanation:
Expected number of votes = np
= \(\frac{70}{100}\) × 120000
= 84000

Question 7.
The last (unit) digit of (22)¹² is
(A) 2
(B) 4
(C) 6
(D) 8
Answer:
(C) 6

Explanation:
We have (22)¹²,
Here, base number is 22 and its units digit is 2.
Also, exponent is 12, which is divisible by 2 (units digit).
i.e., 12 ÷ 2 = 6
So, last digit of (22)¹² is 6.

Question 8.
The present value of a sequence of payment of 1000 made at the end of every 6 months and continuing foreve if money is w&th 8%. per annum compounded semi-annually is
(A) 1000
(b) 2500
(C) 25,000
(D) 15,000
Answer:
(C) 25,000

Explanation:
The given annuity is a perpetuity.
present value of perpetuity = \(\frac{\text { Cash flow }}{\text { Interest rate }}\)
Here, cash flow = ₹ 1000
interest rate = \(\frac{8 / 2}{100}\)
= \(\frac{4}{100}\) = 0.04
So, present value = \(\frac{1000}{0.04}\)
= ₹ 25,000

Question 9.
The value of \(\int_0^1 \frac{1}{\sqrt{1+x^2}}\) dx is
(A) log √2
(B) log (1 + √2)
(C) log (1 – √2)
(D) \(\frac{1}{\log (1+\sqrt{2})}\)
Answer:
(B) log (1 + √2)

Explanation:
\(\int_0^1 \frac{1}{\sqrt{1+x^2}}\) dx = log \(\left|x+\sqrt{1+x^2}\right|_0^1\)
= log \(\left|1+\sqrt{1+1^2}\right|\) – log \(|0+\sqrt{1+0}|\)
= log (1 + √2) – log 1
= log (1 + √2)
[∵ log 1 = 0]

Question 10.
Which of the following is not an example of a time series model?
(A) Naive approach
(B) Exponential smoothing
(C) Moving average
(D) None of these
Answer:
(A) Naive approach

Question 11.
Reenra has an initial investment of ₹ 1,00,000 in an investment plan. After 5 years, it has grown to ₹ 2,00,000 then rate of return is:
(A) 50 %
(B) 100 %
(C) 75 %
(D) 200 %
Answer:
(B) 100 %

Explanation:
Rate of Return = \(\frac{2,00,000-1,00,000}{1,00,000}\) × 100
= 100 %

Question 12.
The effective rate which is equivalent to nominal rate of 10 % p.a. compounded quarterly is
(A) 10.25 %
(B) 10.38 %
(C) 10.47 %
(D) 10.53 %
Answer:
(B) 10.38 %

Explanation:
Amount of ₹ 100 for 1 year when compounded quarterly
= ₹ [100 × (1 + \(\frac{2.5}{100}\))⁴]
= ₹ [100 × (1 + 0.025)⁴]
= ₹ (100 × 1.1038)
= ₹ 110.38
∴ Effective rate = (110.38 – 100)% = 10.38%

[Note: Effective rate which is equivalent to nominal rate of 10% p.a.]
When compounded semi-annually = 10.250 %
When compounded Quarterly = 10.381 %
When compounded monthly = 10.471 %
When compounded daily = 10.516 %

Question 13.
The sum of money is needed now, so as to get ₹ 6000 at the beginning of every month forever, then the money is worth 6% per annum compounded monthly is
(A) ₹ 1000000
(B) ₹ 1206000
(C) ₹ 60,000
(D) ₹ 1600000
Answer:
(B) ₹ 1206000

Explanation:
Given R = 6000,
r = \(\frac{6}{12}\) % = 0.5 per month
So, i = \(\frac{0.5}{100}\) = 0.005
So, P = R + \(\frac{R}{i}\)
= 6000 + \(\frac{6000}{0.005}\)
= 6000 + 1200000
= ₹ 12,06,000

Question 14.
The order and degree (if defined) of differential equation \(\frac{d^2 y}{d x^2}\) + \(\frac{d y}{d x}\) – 6y = 0 are
(A) 1, 1
(B) 2, 1
(C) 1 ,2
(D) 2, 2
Answer:
(B) 2, 1

Explanation:
The highest order derivative present is \(\frac{d^2 y}{d x^2}\) and its raised to power 1.
So, its degree is 1 and its order is 2.

Question 15.
Which of the following is a vertex of the positive region bounded by the inequalities, 2x + 3y ≤ 6 and 5x + 3y ≤ 15
(A) (0, 2)
(B) (0, 0)
(C) (3, 0)
(D) All of these
Answer:
(D) All of these

Explanation:
Here, (0, 2), (0, 0) and (3, 0) all are vertices of feasible region.

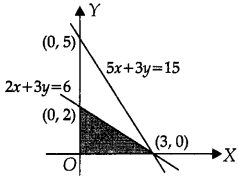
Question 16.
Binomial distribution is a ____________
(A) Continuous distribution
(B) Discrete distribution
(C) Irregular distribution
(D) Not a Probability distribution
Answer:
(B) Discrete distribution

Explanation:
It is applied to discrete random variable, hence it is a discrete distribution.

Question 17.
The following are the movement(s) in file secular trend.
(A) Smooth
(B) Regular
(C) Steady
(D) All of these
Answer:
(D) All of these

Explanation:
Secular trend is that component of the time series which gives the general tendency of the data for a long periods. It is smooth, regular and long term (steady) movement of a series.

Question 18.
A ___________ is a statistical test used to compare the means of two groups.
(A) t-test
(B) p-test
(C) h-test
(D) g-test
Answer:
(A) t-test

DIRECTION:
In the following questions, a statement of Assertion (A) is followed by a.statement of Reason (R). Choose the correct answer out of the following choices.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A) : The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 3x² + 26x + 15. The marginal revenue, when x = 15 is ₹ 116.
Reason (R) : Marginal revenue (MR) is the rate of change of total revenue with respect to the number of units sold.
Therefore, (MR)_{at x = 15} = (\(\frac{d R}{d x}\))_{at x = 15}
Answer:
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).

Explanation:
Here,
R(x) = 3x² + 26x + 15
\(\frac{d R}{d x}\) = 6x + 26
⇒ (\(\frac{d R}{d x}\))_{at x = 15} = 6(15) + 26 = ₹ 116

Question 20.
Assertion (A) : The standard normal curve is symmetric about the value of mean = 0.
Reason (R) : For a standard normal variate, the value of standard deviation is 1.
Answer:
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).

Explanation:
If the mean and standard deviation of a normal variate are 0 and 1, respectively it is called as standard normal variate.
Thus, both the given statements are individually true.

Section – B
(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
Suppose a manufacturing company purchases a machinery for ₹ 100,000 and the useful life of the machinen/are 10 years and the residual value of the machinery is ₹ 20,000. Calculate depreciation.
Answer:
We know that,
Annual Depreciation expense = \(\frac{\text { Asset cost }- \text { Residual Value }}{\text { Useful life of the asset }}\)
= \(\frac{₹ 100,000-₹ 20,000}{10}\)
= ₹ 8,000

Question 22.
If \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & y & 0 \\
0 & 0 & 1
\end{array}\right]\left[\begin{array}{c}
x \\
-1 \\
z
\end{array}\right]=\left[\begin{array}{l}
1 \\
2 \\
1
\end{array}\right]\), find x + y + z.
Answer:
\(\left[\begin{array}{c}
x \\
-y \\
z
\end{array}\right]=\left[\begin{array}{l}
1 \\
2 \\
1
\end{array}\right]\)

x = 1, y = – 2, z = 1
or x + y + z = 0

OR

Solve the following system of equations by Cramer’s rule: 2x – y = 17, 3x + 5y = 6.
Answer:
Given,
2x – y = 17
3x + 5y = 6
Here, ∆ = \(\left|\begin{array}{cc}
2 & -1 \\
3 & 5
\end{array}\right|\)
= 10 + 3 = 13

∆_x = \(\left|\begin{array}{cc}
17 & -1 \\
6 & 5
\end{array}\right|\)
= 85 + 6 = 91

∆_y = \(\left|\begin{array}{cc}
2 & 17 \\
3 & 6
\end{array}\right|\)
= 12 – 51 = – 39
Using Cramer’s rule,
x = \(\frac{\Delta x}{\Delta}\)
= \(\frac{91}{13}\) = 7
and y = \(\frac{\Delta y}{\Delta}\)
= \(\frac{-39}{13}\) = – 3

Question 23.
A firm has to transport at least 1200 packages daily using large vans which carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is ₹ 400 and each small van is ₹ 200. Not more than ₹ 3,000 is to be spent daily on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimize cost.
Answer:
Let the number of large vans and small vans used for transporting the packages be x and y, respectively.
It is given that the cost of engaging each large van is ₹ 400 and each small van is ₹ 200.
Cost of engaging x large van is ₹ 400 and each small van is ₹ 200.
Cost of engaging x large vans = ₹ 400 x
Cost of engaging y small vans = ₹ 200 y
Let Z be the total cost of engaging x large vans and y small vans.
Z = ₹ (400 x + 200 y)
The firm has to transport atleast 1200 packages
daily using large vans which carry 200 packages
each and small vans which can take 80 packages each.
So, 200 x + 80 y ≥ 1200
Not more than 3000 is to be spent daily on the transport.
So, 400 x + 200 y ≤ 3000
Also, the number of large vans cannot exceed the number of small vans.
∴ x ≤ y
Thus, the linear programming problem of the problem is
∴ Min.Z = ₹ (400 x + 200 y)
Subject to constraints
200 x + 80 y ≥ 1200
400 x + 200 y ≤ 3000
x ≤ y
x ≥ 0, y ≥ 0

Question 24.
Two pipes A and B can fill a tank in 24 minutes and 32 minutes respectively, if both the pipes are opened simultaneously, after how much time B should be closed so that the tank is full in 18 minutes?
Answer:
Let B be closed after x minute.
Then, part filled by (A + B) in x min + part filled b3
A in (18 – x) min = 1
∴ x \(\left(\frac{1}{24}+\frac{1}{32}\right)\) + (18 – x) × \(\) = 1
⇒ \(\frac{7 x}{96}+\frac{18-x}{24}\) = 1
⇒ 7x + 4 (18 – x) = 96
⇒ x = 8
Hence, B must be closed after 8 minutes.

OR

Today is Tuesday. My uncle will come after 45 days. In which day my uncle will be coming?
Answer:
Number of days in a week = 7
So, 45 ≡ x (mod 7)
45 ≡ 3 (mod 7)
As

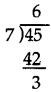
The value of x must be 3.
Thus, three days after Tuesday is Friday.
So, uncle will come on Friday.

Question 25.
In a sample of 400 population from a village 230 are found to be eaters of vegetarian items and the rest non-vegetarian items. Compute the standard error assuming that both vegetarian and non-vegetarian foods are equally popular in that village?
Answer:
Given sample size 400 and 230 are vegetarian eaters.
So sample proportional = \(\frac{230}{400}\) = 0.575
Population proportion P = Prob. (vegetarian eaters from the village) = \(\frac{1}{2}\)
(Since, vegetarian and non-vegetarian foods are equally popular.)
Q = 1 – P
= 1 – \(\frac{1}{2}\)
= \(\frac{1}{2}\)
The standard error S.E. = \(\sqrt{\frac{P Q}{N}}\)
= \(\sqrt{\frac{\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)}{400}}\)
= \(\sqrt{\frac{0.25}{400}}\)
= \(\sqrt{0.000625}\)
= 0.025

Section – C
(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
Find: ∫ \(\frac{2 x+1}{(x+1)(x-2)}\) dx
Answer:
Let \(\frac{2 x+1}{(x+1)(x-2)}=\frac{A}{x+1}+\frac{B}{(x-2)}\)
⇒ 2x + 1 = A (x – 2) + B (x + 1)
Equating the coefficients of x and constant term on both sides, we get
A + B = 2
and – 2A + B = 1
Solving these equations, we get
A = \(\frac{1}{3}\) and B = \(\frac{5}{3}\)
∴ \(\frac{2 x+1}{(x+1)(x-2)}=\frac{1 / 3}{(x+1)}+\frac{5 / 3}{(x-2)}\)
\(\int \frac{2 x+1}{(x+1)(x-2)} d x=\frac{1}{3} \int \frac{d x}{(x+1)}+\frac{5}{3} \int \frac{d x}{(x-2)}\)
= \(\frac{1}{3}\) log |x + 1| + \(\frac{5}{3}\) log |x + 2| + C

OR

Evaluate: \(\int_0^1 \frac{x e^x}{(1+x)^2}\) dx
Answer:
Let I = \(\int_0^1 \frac{x e^x}{(1+x)^2}\) dx

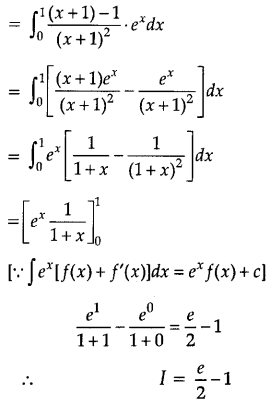
Question 27.
A trust fund has ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to orphanage and second bond pays 10% interest per annuum which will be given to an N.G.O. (Cancer Aid Society). Use matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200.
Answer:
Let investment in first type of bond be ₹ x.
∴ The investment in second type of bond = ₹ (35,000 – x)
∴ [x 35,000 – x] \(\left[\begin{array}{c}
\frac{8}{100} \\
\frac{10}{100}
\end{array}\right]\) = [3,200]
Or, \(\frac{8}{100}\) x + (35,000 – x) \(\frac{10}{100}\) = 3,200
Or, x = ₹ 15,000
∴ Investment in first bond = ₹ 15,000
and Investment in second bond = ₹ (35,000 – 15,000)
= ₹ 20,000

Question 28.
Find the maximum value of \(\left(\frac{1}{x}\right)^x\).
Answer:
Let y = \(\left(\frac{1}{x}\right)^x\)
⇒ log y = x . log \(\frac{1}{x}\)

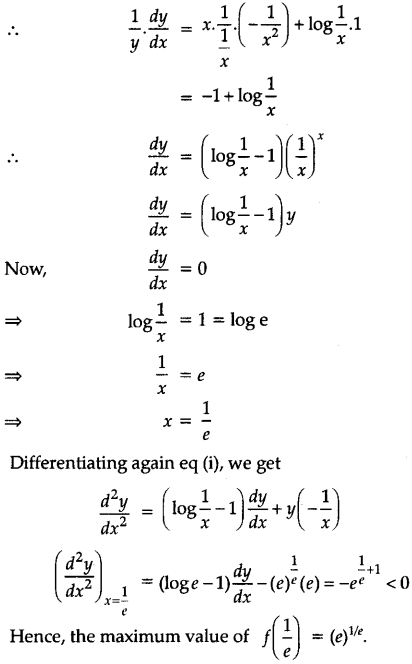
Question 29.
The demand and supply function of an article are D(q) = 1000 – 0.4q² and S(q) – 42q. Find the consumer’s surplus at equilibrium price.
Answer:
Given, D(q) = 1000 – 0.4q²
and S(q) = 42q
At equilibrium D(q) = S(q)
1000 – 0.4q² = 42q
or, 0.4q² + 42q – 1000 = 0
or, 4q² + 420q – 10000 = 0
or, q² + 105q – 2500 = 0
or, (q + 125) (q – 20) = 0
q = – 125 or 20
The value of q cannot be negative, q = 20
When q = Q_e = 20
D(20) = 1000 – 0.4(20)²
= 1000 – 0.4 × 400
= 1000 – 160
= 840 = P_e
Consumer’s surplus is given by
CS = \(\int_0^{Q_f}\) D(q) dq – Q_e . P_e
= \(\int_0^{20}\) (1000 – 0.4q²) dq – 20 × 840
= 1000 \([q]_0^{20}\) – 0.4 \(\left[\frac{q^3}{3}\right]_0^{2 n}\) – 16800
= 1000 (20 – 0) – 0.4 \(\left(\frac{20^3}{3}-0\right)\) – 16800
= 1000 × 20 – 0.4 × \(\frac{8000}{3}\) – 16800
= 20000 – 1066.666 – 16800
= 20000 – 17866666
= 2133.334
= 2133 units

OR

Find the area of the region bounded by the curve y² = x and the lines x = 1, x = 4 and the X-axis.
Answer:

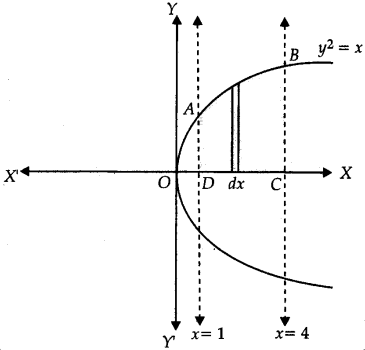
The area of the region bounded by the curve,
y² = x, the lines x = 1 and x = 4, and the X-axis is the area ABCD.
Area of ABCD = \(\int_1^4\) y dx
= \(\int_1^4\) √x dx
= \(\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_1^4\)
= \(\frac{2}{3}\left[(4)^{\frac{3}{2}}-(1)^{\frac{3}{2}}\right]\)
= \(\frac{2}{3}\) [8 – 1]
= \(\frac{14}{3}\) units²

Question 30.
A company borrowed ₹ 60,000 for renovation. The company plans to set up a sinking fund that will pay back the loan at the end of 5 years. Assuming a rate of 10% compounded semiannually and the sinking fund of the ordinary annuity. Given that (1.05)¹⁰ = 1.06288.
Answer:
Given, P = 60,000,
r = 10% or 0.10,
No. of years, n = 5 years
and No. of payments per year, m = 2 (Semi annually)

Question 31.
An interviewer gives the following graph on a client’s sales in the last 7 years to candidate and said find the CAGR. Given that \(\left(\frac{9}{4}\right)^{\frac{1}{7}}\) = 1.1228.

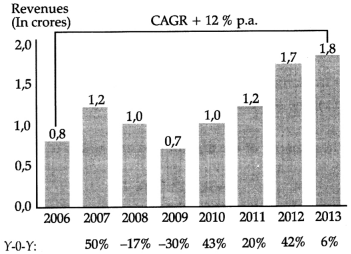
Answer:
Sales in 2006 were 0.8 crores (beginning value).
In 2013, after 7 years, sales increased to 1.8 crores.
CAGR = \(\left(\frac{\text { End value }}{\text { Beginning value }}\right)^{\frac{1}{n}}\) – 1
= \(\left(\frac{1.8}{0.8}\right)^{\frac{1}{7}}\) – 1
= \(\left(\frac{9}{4}\right)^{\frac{1}{7}}\) – 1
= 0.1228
CAGR % = 12.28 %

Section – D
(This section comprises of long answer type questions (LA) of 5 marks each)

Question 32.
An experiment succeeds thrice as often as it fails. Find the probability that in the next 5 trials, there will be atleast 3 successes.
Answer:
Let probability of success be p and that of failure be q
∴ p = 3q,
and p + q = 1
∴ p = \(\frac{3}{4}\)
and q = \(\frac{1}{4}\)
P(atleast 3 successes) = P(r ≥ 3)
= P(3) + P(4) + P(5)
= \({ }^5 C_3\left(\frac{1}{4}\right)^2\left(\frac{3}{4}\right)^3+{ }^5 C_4\left(\frac{1}{4}\right)^1\left(\frac{3}{4}\right)^4+{ }^5 C_5\left(\frac{3}{4}\right)^5\)
= \(\frac{270}{1024}+\frac{405}{1024}+\frac{243}{1024}\)
= \(\frac{918}{1024}=\frac{459}{512}\)

OR

Two cards are drawn simultaneouly (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean and variance of the number of kings.
Answer:
X = no. of kings = 0, 1, 2
P(X = 0) = P (one king)
= \(\frac{48}{52} \times \frac{47}{51}=\frac{188}{221}\)
P(X = 1) = P(one king and one non-king)
= \(\frac{4}{52} \times \frac{48}{51}\) × 2
= \(\frac{188}{221}\)

P(X = 2) = P(two kings)
= \(\frac{4}{52} \times \frac{3}{51}=\frac{1}{221}\)
Probability distribution is given by

X	0	1	2
P(X)	\(\frac{188}{221}\)	\(\frac{32}{221}\)	\(\frac{1}{221}\)

Now, Mean = Σ X . P(X)
= \(\frac{188}{221} \times 0+\frac{32}{221} \times 1+\frac{1}{221} \times 2\)
= \(\frac{34}{221} \text { or } \frac{2}{13}\)

and Var(X) = ΣX² . P(X) – [ΣX. P(X)]²
= \(\frac{188}{221} \times 0+\frac{32}{221} \times 1+\frac{1}{221} \times 4-\left(\frac{34}{221}\right)^2\)
= \(\frac{188}{221} \times 0+\frac{32}{221} \times 1+\frac{1}{221} \times 4-\left(\frac{34}{221}\right)^2\)
= \(\frac{6800}{45541} \text { or } \frac{400}{2873}\)

Question 33.
Two tailors P and Q earn ₹ 150 and ₹ 200 per day respectively. P can stitch 6 shirts and 4 trousers a day, while Q can stitch 10 shirts and 4 trousers per day. How many days should each work to produce at least 60 shirts and 32 trousers at minimum labour cost?
Answer:
Let the tailor P work for x days and the tailor Q work for y days respectively.
Here, the problem can be formulated as an L.P.P as follows:
Minimize Z = 150x + 200y
Subject to the constraints:
6x + 10y ≥ 60 …………….(i)
Or, 3x + 5y ≥ 30
4x + 4y ≥ 32 …………..(ii)
Or, x + y ≥ 8
and x ≥ 0, y ≥ 0 ……………..(iii)
Converting them into equations we obtain the following equations:
3x + 5y = 30,
⇒ y = \(\frac{30-3 x}{5}\)
x + y = 8
⇒ y = 8 – x
3x + 5y = 30

x	0	10	5
y	6	0	3

x + y = 8

x	0	8	5
y	8	0	3

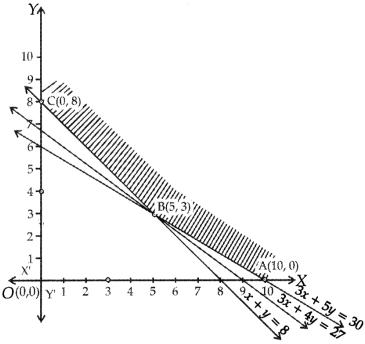
The shaded region in the diagram represent the feasible region.
The corner points are A (10, 0), B (5, 3) and C (0, 8)
At the corner point the value of Z = 150x + 200y
At A (10, 0) Z = 1500
At B (5, 3) Z = 150 × 5 + 200 × 3
= 750 + 600 = 1350
At C (0, 8) Z = 1600
As the feasible region is unbounded, we draw the graph of the half-plane.
150x + 200y < 1350
3x + 4y < 27
There is no point common with the feasible region, therefore, Z has minimum value.
Minimum value of Z is 1350 and it occurs at the point B(5, 3).
Hence, the labour cost is ₹ 1350 when P works for 5 days and Q works for 3 days.

Question 34.
A cone is inscribed in a sphere of radius 12 cm. if the volume of the cone is maximum, find its height.
Answer:
Let r be the radius of cone and h be the height of cone,
let x be the distance between centre of sphere
and centre of base of cone,
Given,
radius of sphere R = 12 cm
∴ h = 12 + x

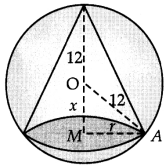
Volume of cone = \(\frac{1}{3}\) πr²h
= π (12² – x²) (12 + x)
(∵ In ∆ OMA, 12² = x² + r²]
= \(\frac{1}{3}\) π (144 – x²) (12 + x)
∴ \(\frac{d V}{d x}\) = \(\frac{1}{3}\) π [(144 – x).1 + (12 + x) (- 2x)]
= \(\frac{1}{3}\) π [144x² – 24x – 2x²]
= \(\frac{1}{3}\) π [144 – 24x – 3x²] dV
For maximum or minimum volume, put \(\frac{d V}{d x}\) = 0
i.e., \(\frac{1}{3}\) π (144 – 24x – 3x²) = 0
⇒ 144 – 24x – 3x² = 0
⇒ x² + 8x – 48 = 0
⇒ (x + 12) (x – 4) = 0
⇒ x = – 12 and x = 4
Now,
\(\frac{d^2 V}{d x^2}\) = \(\frac{1}{3}\) π [- 24 – 6x]
∴ (\(\frac{d^2 V}{d x^2}\))_{x = 4} = \(\frac{1}{3}\) π [- 24 – 24] < 0

OR

Assume that a spherical raindrop evaporates at a rate proportional to its surface area. If the radius originally in 3 mm and 1 hour later has been reduced to 2 mm, find an expression for the radius of the rain drop at any time.
Answer:
Let r(t) denotes the radius of the raindrop after t minutes.
Since, given the radius is decreasing as t increases, the rate of change of r must be negative.
Let V be the volume of the raindrop and S be its surface area

⇒ ∫ dr = – ∫ k dt
⇒ r = – kt + C ………….(ii)
Given, when t = 0, r = 3 mm
∴ from eq (ii), we get C = 3
Now, r(t) = – kt + 3 ……………..(iii)
Also, when t = 1, r = 2 mm
∴ from eq.(iii),
r(1) = – k × 1 + 3
Or, 2 = – k + 3
Or, k = 1
Therefore, – 2t + 3 is the required expression.

Question 35.
Using matrix method, solve the following system of equations for x, y and z:
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
Answer:
Given system of equations:
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
This can be written as AX = B
where A = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
2 & 1 & -3 \\
1 & 1 & 1
\end{array}\right]\),
X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\)
B = \(\left[\begin{array}{l}
4 \\
0 \\
2
\end{array}\right]\)
Here, |A| = 1 (1 + 3) + 1 (2 + 3) + 1 (2 – 1)
= 4 + 5 + 1
= 10
Since, |A| ≠ 0
Hence, the system of equations is consistent and
has a unique solution given by X = A^-1B
A^-1 = \(\frac{\ {adj} A}{|A|}\)
and adj A = C^T

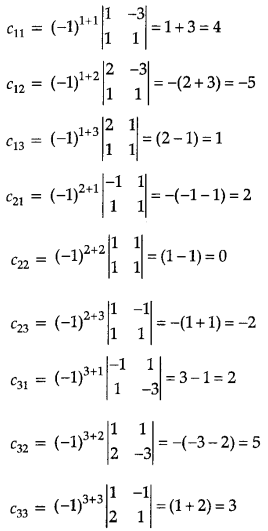
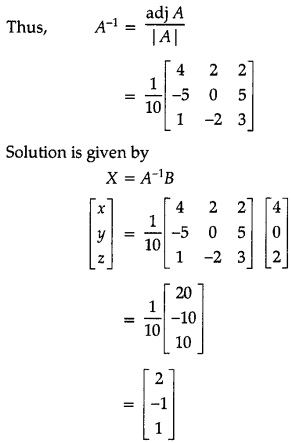
Thus, solution is x = 2, y = – 1 and z = 1.

Section – E
(This section comprises of 3 source based questions (Case Studies) of 4 marks each)

CASE STUDY – I

Question 36.
Read the following text and answer the following questions on the basis of the same:

Today Seema learns two properties of Modulo operator in class which are as follows;
Property 1 :
If the value of X is increased by a multiple of Y (Say, kY), where k is any integer)
Then X mod Y = (X + kY) mod Y; where k is any integer.

Property 2 :
Addition property of modulo arithmetic is if A, B and C are positive integers then,
(A + B) mod C = (A mod C + B mod C) mod C

(i) Evaluate: (7 + 6 × 3) mod 3
Answer:
(7 + 6 × 3) mod 3
= 7 (mod 3) [from property I]
= 1

OR

Evaluate: (12 + 18) mod 4
Answer:
(12 + 18) mod 4
= (12 (mod 4) + 18 (mod 4)) mod 4
= 0 + 2 (mod 4)
= 2

(ii) If k = 12, ky = 60 and X = 18, then find X (mod Y).
Answer:
Here, k = 12, ky = 60
So, Y = 5
∴ X (mod Y) = 18 (mod 5) = 3

(iii) (a) Express (18 + 9 × 6) mod 6 in form of X mod Y.
Answer:
Since,
(X + kY) mod Y = X mod Y
Therefore, (18 + 9 × 6) mod 6 = 18 mod 6

(b) Evaluate: – 97 mod 11
Answer:
When – 97 divided by 11, we get
Quotient = 8
and remainder = – 9
But since this remainder is negative, we have to increase our quotient by 1 to say – 97 divided by 11
equals – 9 remainder 2, as 11 (- 9) + 2 = – 97.

CASE STUDY – II

Question 37.
A factory produces bulbs, of which 6% are defective bulbs in a large bulk of bulbs.
Based on the above information, answer the following questions:

(i) Find the probability that in a sample of 100 bulbs selected at random, none of the bulbs is defetive.(Use: e^-6 = 0.0024)
Answer:
Given, n = 100,
p = 6% = 0.06
∴ Mean, np = 100 × 0.06 = 6(λ)
(i) P(X = r) = \(\frac{e^{-\lambda} \lambda^r}{r !}\)
P(X = 0) = \(\frac{e^{-6} 6^0}{0 !}\)
= e^-6
= 0.0024 (Given)

(ii) Find the probability that the sample of 100 bulbs has exactly two defective bulbs.
Answer:
P (X = 2) = \(\frac{e^{-6} 6^2}{2 !}\)
= \(\frac{e^{-6} \cdot 36}{2}\)
= e^-6 × 6
= 0.0024 × 18
= 0.0432

(iii) (a) Find the probability that the sample of 100 bulbs will include not more than one defective bulb.
Answer:
P (X = 1) = \(\frac{e^{-6} 6^1}{1 !}\)
= e^-6 × 6
= 00024 × 6
= 0.0144
Now, Probability that sample of 100 bulbs will include not more than one defective bulb
P(X ≤ 1) = P(X = 0) + P (X = 1)
= [0.0024 + 0.01441]
= 0.016

OR

(b) Find the mean and the variance of the distribution of number of defective bulbs in a sample of 100 bulbs.
Answer:
We know that mean and variance of the Poisson distribution are same.
Thus, mean = 6
and variance = 6.

CASE STUDY – III

Question 38.
Fit the straight line trend to the following time series data:

Answer:

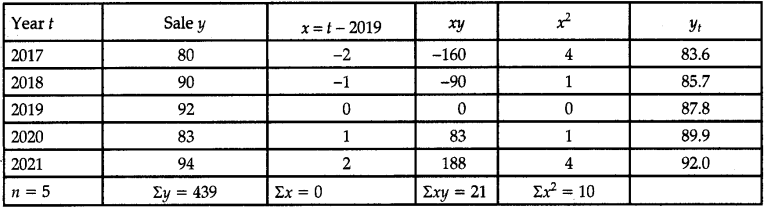
Now,
a = \(\frac{\sum y}{n}\)
= \(\frac{439}{5}\)
= 87.8
b = \(\frac{\sum x y}{\sum x^2}\)
= \(\frac{21}{10}\)
= 2.1
Hence, trend equation is
y_t = 87.8 + 2.1x

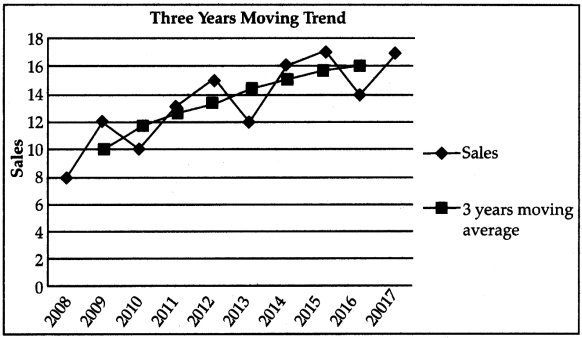
From the following time series obtain trend value by 3 yearly moving averages. Also, draw the moving averages graph.

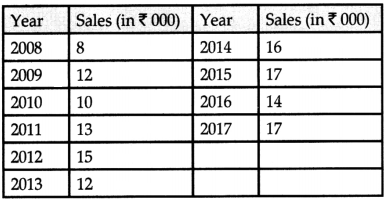
Answer:
Calculation of trend values by three yearly moving average method.