CBSE Sample Papers for Class 12 Applied Maths Set 10 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Maths with Solutions and marking scheme Set 10 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Maths Set 10 with Solutions

Time Allowed : 3 hours
Maximum Marks : 80

General Instructions:

1. This Question paper contains – five sections A,B,C,D and E. Each section is compulsory. However, there is some internal ‘ choice in some questions.
2. Section A has 18 MCQ’s and 02 Assertion Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
4. Section C has 6 Short Answer (SA) questions of 3 marks each.
5. Section D has 4 Long Answer (LA) questions of 5 marks each.
   Section E has 3 source based/case based/passage based/integrated units of assessment (04 marks each) with sub parts.
6. Internal Choice is provided in 2 questions in Section-B, 2 questions in Section-C, 2 Questions in Section-D. You have to attempt only one alternatives in all such questions.

Section – A
(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
The value of 5 ₈ 11, where is multiplication modulo is
(A) – 1
(B) 0
(C) 7
(D) 9
Answer:
(C) 7

Explanation:
5 ₈ 11 = (5 × 11) mod 8
= 55 mod 8
= 7

Question 2.
The solution of \(\frac{x-3}{x+5}\) > 0, x ≠ – 5, x ∈ R is
(A) x > 3
(B) x <-5
(C) x < – 5 or x > 3
(D) no solution
Answer:
(C) x < – 5 or x > 3

Explanation:
Given, \(\frac{x-3}{x+5}\) > 0, x ≠ – 5
Multiplying by (x + 5)²
(x + 5) (x – 3) > 0

∴ Solution (- ∞, – 5) ∪ (3, ∞)
Or, x < – 5 x > 3

Question 3.
A specific characteristics of a sample is known as
(A) population
(B) parameter
(C) statistic
(D) variance
Answer:
(C) statistic

Question 4.
Which of the following statements are true?
I : The mean of a population is denoted by x
II : The population mean is a statistic.
(A) Ionly
(B) II only
(C) Both I and II
(D) None
Answer:
(B) II only

Question 5.
A retailer buys 250 kg of rice, a part of which he sells at 10% profit and the remaining at 5% loss. If the net profit made by the retailer in the whole transaction is 7%, then the quantity of rice sold at 10% profit is
(A) 200 kg
(B) 150 kg
(C) 100 kg
(D) 50 kg
Answer:
(A) 200 kg

Explanation:
C = – 5 %
d = 10 %
m = 7 %
(d – m) : (m – c) = 1 : 4
Quantity sold at 10% Profit = \(\frac{4}{5}\) × 20
= 200 kg

Question 6.
If the mean of a binomial distribution is 81, then the standard deviation lies in the interval
(A) [0, 9)
(B) (0, 9]
(C) [0, 3]
(D) (0, 3]
Answer:
(A) [0, 9)

Explanation:
Standard deviation, σ = \(\sqrt{n p q}\) ≥ 0
Now,
mean = np = 81
and q < 1
So, σ = \(\sqrt{n p q}\) < \(\sqrt{n p}\)
= \(\sqrt{81}\) = 9
∴ 0 ≤ σ < 9
Hence, a lies in [0, 9).

Question 7.
If a = b (mod n), then
(A) a^k = b^k (mod n) ∀ k ∈ N
(B) k_a = k_b (mod n) ∀ k ∈ I
(C) Both A and B
(D) Only A
Answer:
(C) Both A and B

Question 8.
If C is the original cost of an asset, S is the salvage value of the asset and n is the number of year estimated for useful life of the asset, the annual depreciation of the asset is given by
(A) D = \(\frac{C-S}{n}\)
(B) D = \(\frac{S-C}{n}\)
(C) D = \(\frac{C+S}{n}\)
(D) D = \(\frac{S}{n}\) × n
Answer:
(A) D = \(\frac{C-S}{n}\)

Question 9.
The value of : ∫ [√x + \(\frac{1}{\sqrt{x}}\)]² dx is
(A) x² – 2x + log | x | + C
(B) \(\frac{x^2}{2}\) + 2x + log |x| + C
(C) x² + 2x – log |x| + C
(D) x² – x + log |x| + C
Answer:
(B) \(\frac{x^2}{2}\) + 2x + log |x| + C

Explanation:
Let I = ∫ [√x + \(\frac{1}{\sqrt{x}}\)]² dx
= ∫ (x + \(\frac{1}{x}\) + 2) dx
= ∫ x dx + ∫ \(\frac{1}{x}\) dx + 2 ∫ dx
= \(\frac{x^2}{2}\) + 2x + log |x| + C

Question 10.
Which of the following can’t be a component for a time series plot?
(A) Seasonality
(B) Trend
(C) Noise
(D) None of these
Answer:
(D) None of these

Question 11.
Your grandfather is retiring at the end of next year. He would like to ensure that his heirs receive payments of ₹ 75,000 a year forever, starting when he retires. How much does he need to invest in the beginning of this year to produce the desired cash flow, if money is worth 6% compounded annually?
(A) ₹ 12,50,000
(B) ₹ 11,50,000
(C) ₹ 12,00,000
(D) ₹ 12,05,000
Answer:
(A) ₹ 12,50,000

Explanation:
Given, R = ₹ 75,000
and i = \(\frac{6}{100}\) = 0.06
Present value, P = \(\frac{R}{i}\)
P = \(\frac{75,000}{0.06}\)
= ₹ 12,50,000

Question 12.
What is the face value of a sinking fund that yields a dividend of ₹ 1800 at 10% semi-annually?
(A) ₹ 3600
(B) ₹ 18000
(C) ₹ 124000
(D) ₹ 36000
Answer:
(D) ₹ 36000

Explanation:
Let the face value of the sinking fund = x
Then, \(\frac{10}{200}\) x = 1800
⇒ x = ₹ 36000

Question 13.
Navisha has an initial investment of ₹ 2,00,000 in an investment plan. After 6 years, it has grown to 2,50,000 then rate of return is
(A) 25 %
(B) 55 %
(C) 75 %
(D) 80 %
Answer:
(A) 25 %

Explanation:
Rate of Return = \(\frac{250000-200000}{200000}\) × 100 = 25 %

Question 14.
The order and degree (if defined) of differential equation \(\) = 0 are:
(A) 1, 2
(B) 2, 1
(C) 1, 1
(D) 4, 2
Answer:
(B) 2, 1

Explanation:
The highest order derivative present is \(\frac{d^2 S}{d t^2}\) and it is raised to power 1.
So, its order is 2 and degree is 1.

Question 15.
Region represented by x ≥ 0, y ≥ 0 lies in
(A) I quadrant
(B) II quadrant
(C) III quadrant
(D) IV quadrant
Answer:
(A) I quadrant

Explanation:
Since, x and y both take positive values, so region lies in I quadrant.

Question 16.
The expectation of a random variable X (continuous or discrete) is given by
(A) Σ X f(x), ∫ X f(X)
(B) Σ X² f(X), ∫ X² f(X)
(C) Σ f(X), ∫ f(X)
(D) Σ X ∫ f(X), ∫ X f(X²)
Answer:
(A) Σ X f(x), ∫ X f(X)

Explanation:
The expectation of a random variable X is given by the summation (integral) of X times the function in its interval. If it is a continuous random variable, then summation is used and if it is discrete random variable, then integral is used.

Question 17.
In the measurement of the secular trend, the moving averages
(A) Smooth out the time series
(B) Given the trend in a straight line
(C) Measure the seasonal Variations
(D) None of these
Answer:
(A) Smooth out the time series

Explanation:
Moving averages is a series of arithmetic, means of variate values of a sequence.
This is anbther way of drawing a smooth curve for a time series data.

Question 18.
In a school, a random sample of 145 students is taken to check whether a student’s average calory intake is 1500 or not. The collected data of average calories intake of sample students is presented in a frequency distribution, which is called a
(A) Statistics
(B) Sampling distribution
(C) Paremeter
(D) Pbpulation sampling
Answer:
(B) Sampling distribution

DIRECTION:
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A) : The function given by f(x) = 3x + 17 is strictly increasing on R.
Reason (R) : The logarithmic function is strictly increasing on (0, ∞).
Answer:
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).

Explanation:
Assertion (A) is true because
Let x₁ and x₂ be any two numbers in R.
Then we have x₁ < x₂
⇒ 3x₁ < 3x₂
⇒ 3x₁ + 17 < 3x₂ + 17
⇒ f(x₁) < f(x₂)
Hence, f is strictly increasing on R.
Reason (R) is correct because
The given function is f(x) = log x.
∴ f'(x) = \(\frac{1}{x}\)
It is clear that for x > 0, f'(x) = \(\frac{1}{x}\) > 0
Hence, f(x) = log x is strictly increasing in interval (0, ∞).
But Reason (R) is not correct explanation of Assertion (A).

Question 20.
Assertion (A) : Poisson distribution is applied for discrete random variable.
Reason (R) : In a Poisson distribution, the mean and variance are equal.
Answer:
(A) Both (A) and (R) are true and (R) is the correct explanation of (A).

Explanation:
Poisson distribution is a discrete function, means that the variable can only take specific values i.e., 1, 2, …….. etc. with no fraction or decimals.
Also, for Poisson distribution mean = variance = np
Thus, both Assertion and Reason are correct.

Section – B
(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
Assume that the year-end revenues of a business over a three-year period, are mentioned in the following table:

Year – End	31-12-2017	3-12-2020
Year – End Revenue	9,000	3,000

Calculate the CAGR of the revenues over the three-years period spanning the “end” of 2017 to the “end” of 2020. Given that \(\left(\frac{13}{9}\right)^{\frac{1}{3}}\) = 1.13.
Answer:
The CAGR of the revenues over the three-year period spanning the “end” of 2017 to the “end” of 2020 is:
\(\left(\frac{\text { Final value }}{\text { Initial value }}\right)^{\frac{1}{n}}\) – 1
= \(\left(\frac{13000}{9000}\right)^{\frac{1}{3}}\) – 1
= 1.13 – 1
= 0.13
= 13 %

Question 22.
Prove that the diagonal elements of a skew symmetric matrix are all zero.
Answer:
Let A be a skew-symmetric matrix.
Then by definition A’ = – A
or the (i, j)^th element of A’ = the (i, j)^th element of (- A)
or the (j, i)^th element of A = – the (i, j)^th element of A
For the diagonal elements i = j or
the (i, j) the element of A = – the (i, j)th element of A or
the (i, j)th element of A = 0
Hence, the diagonal elements are all zero.

OR

Without expanding at any stage, find the value of \(\left|\begin{array}{ccc}
a & b & c \\
a+2 x & b+2 y & c+2 z \\
x & y & z
\end{array}\right|\).
Answer:
Let ∆ = \(\left|\begin{array}{ccc}
a & b & c \\
a+2 x & b+2 y & c+2 z \\
x & y & z
\end{array}\right|\)
Applying R₁ ⇒ R₁ + 2R₃, we get

Question 23.
A book publisher sells a hard cover edition of a book for ₹ 72 and a paperback edition for ₹ 40. In addition to a fixed weekly cost of ₹ 9,600, the cost of printing hardcover and paperback editions are ₹ 56 and ₹ 28 per book respectively. Each edition requires 5 minutes on the printing machine whereas hardcover binding takes 10 minutes and paperback takes 2 minutes on the binding machine. The printing machine and the binding machine are available for 80 hours each week. Formulate the linear programming problem to maximise the publisher’s profit.
Answer:
Let the number of hardcopy and paperback copies
be x and y respectively
⇒ Maximum profit Z = (72x + 40y) – (9600 + 56x + 28y)
= 16x + 12y – 9600

Subject to constraints:
x + y ≤ 960
5x + y ≤ 2400
xy ≥ 0

Question 24.
Find (186 × 93) mod 7.
Answer:
We know that,
a . b (mod n) ≡ a(mod n) . b(mod n)
So, (186 × 93) mod 7 ≡ 186 (mod 7) . 93 (mod 7)
≡ 4 (mod 7) . 2 (mod 7)
≡ 4 . 2 (mod 7)
≡ 8 (mod 7)
≡ 1 (mod 7)

OR

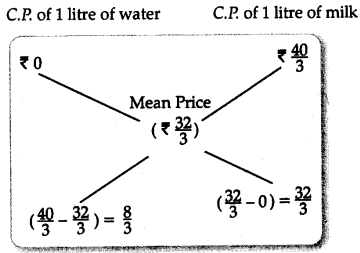
How much water must be added to 60 litres of milk at 1\(\frac{1}{2}\) litres for ₹ 20 so as to have a mixture worth ₹ 10\(\frac{2}{3}\) a litre?
Answer:
C.P of 1 litre of milk = ₹ (20 × \(\frac{2}{3}\))
= ₹ \(\frac{40}{3}\)

Question 25.
The standard deviation of a sample of size 50 is 6.3. Determine the standard error whose population standard deviation is 6?
Answer:
Sample size n = 50
Sample S.D. s = 6.3
Pbpulation S.D. σ = 6
The standard error for sample S.D. is given by
S.E. = \(\sqrt{\frac{\sigma^2}{2 n}}\)
= \(\frac{6}{\sqrt{2(50)}}\)
= \(\frac{6}{\sqrt{100}}\)
= 0.6
Thus standard error for sample S.D. = 0.6

Section – C
(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
Evaluate: ∫ \(\frac{3 x+1}{\left(x^3-x^2-x+1\right)}\) dx
Answer:
Let I = ∫ \(\frac{3 x+1}{\left(x^3-x^2-x+1\right)}\) dx
I = ∫ \(\frac{3 x+1}{(x-1)^2(x+1)}\) dx
Resolving the integrand into partial fractions.
\(\frac{3 x+1}{(x-1)^2(x+1)}=\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x+1}\) …………..(i)
3x + 1 = A (x – 1) (x + 1) + B(x + 1) + C(x – 1)²
⇒ 3x + 1 = x² (A + C) + x (B – 2C) + (- A + B + C)
⇒ A + C = 0,
B – 2C = 3,
– A + B + C = 1
On solving we get A = \(\frac{1}{2}\), B = 2, C = – \(\frac{1}{2}\)
From (i),

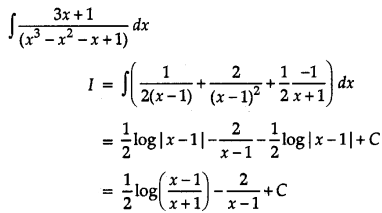
OR

Evaluate: \(\int_{-3}^3\) |x + 2| dx
Answer:
\(\int_{-3}^3\) |x + 2| dx

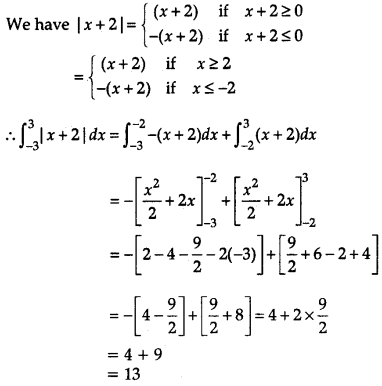
Question 27.
Ishan wants to donate a rectangular plot of land for a school in his village. When he was asked to give dimensions of the plot, he told that if its length is decreased by 50 m and breadth is increased by 50 m, then its area will remain the same. But if length is decreased by 10 m and breadth is decreased by 20 m, then its area will decrease by 5300 m². Using matrices, find the dimensions of the plot.
Answer:
Let length be x m
and breadth be y m.
∴ (x – 50) (y + 50) = xy
⇒ 50x – 50y = 2500
or x – y = 50
and (x – 10) (y – 20) = xy – 5300
⇒ 2x + y = 550
\(\left(\begin{array}{cc}
1 & -1 \\
2 & 1
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)=\left(\begin{array}{c}
50 \\
550
\end{array}\right)\)
⇒ \(\left(\begin{array}{l}
x \\
y
\end{array}\right)=\frac{1}{3}\left(\begin{array}{cc}
1 & 1 \\
-2 & 1
\end{array}\right)\left(\begin{array}{c}
50 \\
550
\end{array}\right)\)
= \(\frac{1}{3}\left(\begin{array}{l}
600 \\
450
\end{array}\right)\)
⇒ x = \(\frac{1}{3}\) (600) = 200 m,
y = \(\frac{1}{3}\) (450) = 150 m

Question 28.
Find the intervals in which the function f(x) = – 2x³ – 9x² – 12x + 1 is
(i) Strictly increasing
(ii) Strictly decreasing.
Answer:
We have,
f(x) = – 2x³ – 9x² – 12x + 1

Now, f'(x) = – 6x² – 18x – 12
= – 6 [x² + 3x + 2]
= – 6 [x² + 2x + x + 2]
Now, f'(x) = – 6x² – 18x – 12
= – 6 [x² + 3x + 2]
= – 6 [x² 2x + x + 2]
f’(x) = – 6 (x + 1) (x + 2)
Put, f’(x)= 0
⇒ x = – 2, x = – 1
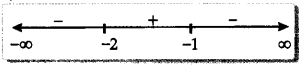
Intervals are (- ∞, – 2), (- 2, – 1) and (- 1, ∞)
Getting f’(x) > 0 in (- 2, – 1) and f’(x) < 0 in (- ∞, – 2) ∪ (- 1, ∞)
⇒ f(x) is strictly increasing in (- 2, – 1)
and strictly decreasing in (- ∞, – 2) ∪ (- 1, ∞)

Question 29.
Find the area of region bounded by the curve x = 2y + 3, Y-axis and the lines y = 1 and y = – 1.
Answer:

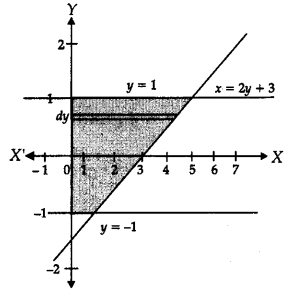
From the figure, area of the shaded region,
A = \(\int_{-1}^1\) (2y + 3) dy
= \(\left[y^2+3 y\right]_{-1}^1\)
= [1 + 3 – 1 + 3]
= 6 sq. units

OR

The demand and supply function of a commodity are P_d = 18 – 2x – x² and P_s = 2x – 3. Find the Producer7s surplus at equilibrium price.
Answer:
Given P_d = 18 – 2x – x²
P_s = 2x – 3
We know that at equilibrium prices P_d = P_s
18 – 2x – x² = 2x – 3
x² + 4x – 21 = 0
(x – 3) (x + 7) = 0
x = – 7 or 3
The value of x cannot be negative, x = 3
When x = Q_e = 3
∴ P_e = 18 – 2(3) – (3) 2 = 3
Producer’s surplus is given by
PS = Q_e . P_e – \(\int_0^Q\) S(x) dx
Here, S(x) = P_S
= (3 × 3) – \(\int_0^3\) (2x – 3) dx
= 9 – \(\left(x^2-3 x\right)_0^3\)
= 9 – (9 – 9)
= 9 units
Hence, at equilibrium price, the producer’s surplus is 9 units.

Question 30.
Mr. Lal took a car loan of ₹ 10 lakhs at an 11% interest for a 15 years loan tenure. What would be his EMI? Given (1.0091)¹⁸⁰ = 5.1069.
Answer:
Given, i = \(\left[\frac{\left(\frac{\text { annual rate }}{12}\right)}{100}\right]\)
= \(\left[\frac{\left(\frac{11}{12}\right)}{100}\right]\)
= \(\frac{0.9166}{100}\)
= 0.0091
n = 15 × 12 = 180
P = ₹ 10,00,000

Question 31.
A firm anticipates an expenditure of ₹ 5,00,000 for plant modernization at end of 10 years from now. How much should the company deposit at the end of year into a sinking fund earning interest 5% per annum. (Given log 1.05 = 0.0212, antilog (0.2120) = 1.6291]
Answer:
Given, A = ₹ 5,00,000
r = 5 %
and n = 10
Using formula, A = p \(\left[\frac{(1+i)^n-1}{i}\right]\)
where i = \(\frac{r}{100}\)
⇒ 500000 = p \(\left[\frac{(1+0.05)^{10}-1}{0.05}\right]\)
[∵ i = \(\frac{5}{100}\) = 0.05]
⇒ p = \(\frac{500000 \times 0.05}{(1.05)^{10}-1}\)
Now, let x = (1.05)¹⁰
Taking log both sides, we get
log x = 10 log (1.05)
= 10 × 0.0212
= 0.2120
⇒ x = antilog (0.2120)
= 1.629
Thus, (1.05)¹⁰ = 1.629
Now, p = \(\frac{500000 \times 0.05}{1.629-1}\)
= \(\frac{25000}{0.629}\)
= 39745.63
Hence, the company should deposit ₹ 39745.63 every year into the sinking fund.

Section – D
(This section comprises of long answer type questions (LA) of 5 marks each)

Question 32.
The average daily sale of ₹ 550 branch offices was ₹ 150 thousand and standard deviation is ₹ 15 thousand. Assuming the distribution to be normal, indicate how many branches have sales between
(i) ₹ 1,25,000 and ₹ 1,45,000
(ii) ₹ 1,40,000 and ₹ 1,60,000
Answer:
Given, that mean µ = 150
and standard deviation σ = 15
(i) When X = 125 thousand
Z = \(\frac{X-\mu}{\sigma}\)
= \(\frac{125-150}{15}\)
= – 1.667
When X = 145 thousand
Z = \(\frac{X-\mu}{\sigma}\)
= \(\frac{145-150}{15}\)
= – o.33

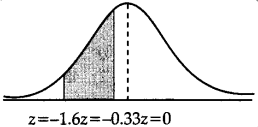
Area between Z = 0 and Z = – 1.67 is 0.4525
Area between Z = 0 and Z = – 0.33 is 0.1293
P(- 1.667 ≤ Z ≤ – 0.33) = 0.4525 – 0.1293 = 0.3232
Therefore the number of branches having sales between ₹ 1,25,000 and ₹ 1,45,000 is 550 × 0.3232 = 178.

(ii) When X = 140 thousand
Z = \(\frac{X-\mu}{\sigma}\)
= \(\frac{140-150}{15}\)
= – 0.67
When X = 160 thousand
Z = \(\frac{X-\mu}{\sigma}\)
= \(\frac{160-150}{15}\)
= 0.67

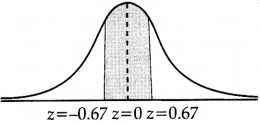
P(- 0.67 < Z < 0) = P (- 0.67 < Z < 0.67) + P (0 < Z < 0.67)
= P (0 < Z < 0.67) + P(0 < Z < 0.67)
= 2P(0 < Z < 0.67)
= 2 × 0.2486
= 0.4972
Therefore, the number of branches having sales between ₹ 1,40,000 and ₹ 1,60,000
= 550 × 0.4972
= 273

OR

Five bad oranges are accidentally mixed with 20 good ones. 1f four oranges are drawn one by one successively with replacement, then find the probability distribution of number of bad oranges drawn. Hence, find the mean and variance of the distribution.
Answer:
Total number of oranges = 25
number of good oranges = 20
number of bad oranges = 5
Probability of getting a bad orange,
P (bad oranges) = \(\frac{5}{25}=\frac{1}{5}\)
Now p = \(\frac{1}{5}\)
q = 1 – p
= \(\frac{4}{5}\)
Let X be the random variable of “Number of bad oranges”.
or X = 0, 1, 2, 3, 4.
P(X = r) = ⁿC_r q^{n – r} . p^r

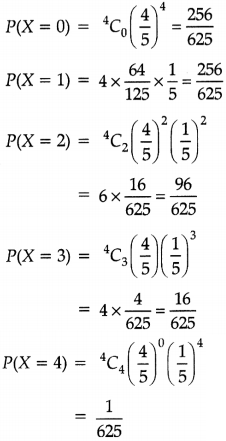
X	P(X)	XP(X)	X2P(X)
0	256/625	0	0
1	256/625	256/625	256/625
2	96/625	192/625	384/625
3	16/625	48/625	144/625
4	1/625	4/625	16/625

∴ Mean = Σ X P(X)
= \(\frac{500}{625}=\frac{20}{25}=\frac{4}{5}\)
Var. (X) = E(X²) – [E(X)]²
= \(\frac{800}{625}-\frac{16}{25}\)
Var.(X) = \(\frac{32}{25}-\frac{16}{25}=\frac{16}{25}\)

Question 33.
A company produces two types of items, P and Q. Manufacturing of both items requires the metals gold and copper. Each unit of item P requires 3 gms of gold and 1 gm of copper while that of item Q requires 1 gm of gold and 2 gm of copper. The company has 9 gm of gold and 8 gm of copper in its store. If each unit of item P makes a profit of ₹ 50 and each unit of item Q makes a profit of ₹ 60, determine the number of units of each item that the company should produce to maximize profit. What is the maximum profit?
Answer:

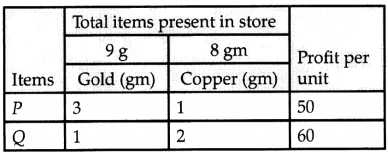
Let x₁ = number of units of item P
= number of units of item Q
Max. Z = 50 x₁ + 60 x₂
Subject to the constraints
3x₁ + x₂ ≤ 9
x₁ + 2x₂ ≤ 8
such that x₁, x₂ ≥ 0
Now, 3x₁ + x₂ = 9 ………………. (i)

x1	0	3
x2	9	0

and x₁ + 2x₂ = 8 ………………..(ii)

x1	0	8
x2	4	0

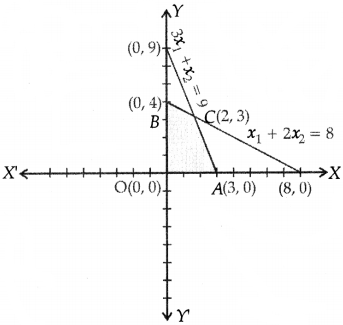
Then corner points of the feasible region are O (0, 0), A (3, 0), B (0, 4) and C (2, 3)

Corner points	Z = 50x1 + 60x2
at O (0, 0),	Z = 0
at A (3, 0),	Z = 50 × 3 + 60 × 0 = 150
at C(2, 3),	Z = 50 × 2 + 60 × 3 = 280
at B(0, 4),	Z = 50 × 0 + 60 × 4 = 240

∴ The company should produce 2 items of type P and 3 items of type Q.
∴ Maximum profit = ₹ 280

Question 34.
An open tank with a square base and vertical sides is to be costructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when depth of the tank is half of its width.
Answer:
Let side of base = x
and depth of tank = y
V = x²y
⇒ y = \(\frac{V}{x^2}\)
(V = Quantity of water = constant)
Cost of material ¡s least when area of sheet used is minimum
A (Surface area of tank) = x + 4xy
= x + \(\frac{4 V}{x}\)
\(\frac{d A}{d x}\) = 2x – \(\frac{4 V}{x^2}\)
\(\frac{d A}{d x}\) = 0
⇒ x³ = 2V,
⇒ x³ = 2x²y,
[as V = x²y]
Therefore,
y = \(\frac{x^3}{2 x^2}=\frac{x}{2}\)
\(\frac{d^2 A}{d x^2}\) = 2 + \(\frac{8 V}{x^3}\) > 0
∴ Area is minimum, thus cost is minimum when y = \(\frac{x}{2}\).

OR

Divide a number 15 into two parts such that the square of one part multiplied with the cube of the other part is maximum.
Answer:
Let the two numbers be x and y.
Then x + y = 15 …………….(i)
ATQ,
P = x²y³
Or, P = x² (15 – x)³ ……………(ii) [from eq. (i)]
Now, \(\frac{d P}{d x}\) = 2x (15 – x)³ + 3x² (15 – x)² (- 1)
Or, \(\frac{d P}{d x}\) = 2x (15 – x)³ – 3x² (15 – x)²
For maximum or minimum value of P, put \(\frac{d P}{d x}\) = 0
i.e.,2x (15 – x)³ – 3x² (15 – x)² = 0
⇒ 2x (15 – x) = 3x²
⇒ 30x – 2x² = 3x²
⇒ x = 6
From eq (1), we get
y = 9
Thus, x = 6 and y = 9
Again, \(\frac{d^2 P}{d x^2}\) = 2 (15 – x)³ – 6x(15 – x)² – 6x(15 – x)² + 6x² (15 – x)
= 2(15 – x)³ – 12x (15 – x)² + 6x² (15 – x)
At x = 6
\(\frac{d^2 P}{d x^2}\) = 2(9)³ – 12 × 6(9)² + 6 × (6)²(9)
= 1458 – 5832 + 1944
= 3402 – 5832
= – 2430 < 0
Thus, P is maximum when x = 6 and y = 9.

Question 35.
Using properties of determinants, prove that \(\left|\begin{array}{ccc}
\frac{(a+b)^2}{c} & c & c \\
a & \frac{(b+c)^2}{a} & a \\
b & b & \frac{(c+a)^2}{b}
\end{array}\right|\) = 2 (a + b + c)³.
Answer:
L.H.S. = \(\frac{1}{a b c}\left|\begin{array}{ccc}
(a+b)^2 & c^2 & c^2 \\
a^2 & (b+c)^2 & a^2 \\
b^2 & b^2 & (c+a)^2
\end{array}\right|\)
C₁ → C₁ – C₃,
C₂ → C₂ – C₃
= \(\frac{1}{abc}\)

Section – E
(This section comprises of 3 source based questions (Case Studies) of 4 marks each)

CASE STUDY-1

Question 36.
An overhead water tank has three pipes A, B and C attached to it (as shown in figure (II)). The inlet pipes A and B can fill the empty tank independently in 15 hours and 12 hours respectively. The outlet pipe C alone can empty a full tank in 20 hours.
Based on the above information, answer the following questions. Show steps to support your answers.

(i) For a routine cleaning of the tank, the tank needs to be emptied. If pipes A and B are closed at the time when the tank is filled to two-fifth of its total capacity, how long will pipe C take to empty the tank completely?
Answer:
Pipe C empties I tank in 20 h
⇒ \(\frac{2}{5}\)th tank in = \(\frac{2}{5}\) × 20 = 8 hours

OR

How long will it take for the empty tank to fill completely. If all the three pipes are opened simultaneously?
Answer:
Part of tank filled in 1 hour = \(\frac{1}{2}\)
= \(\frac{1}{10}\)^th
⇒ time taken to fill tank completely = 10 hours

(ii) Given that the tank is half-full, only pipe C is opened at 6 AM, to empty the tank, after closing the pipe C and an hour’s cleaning time, tank is filled completely by pipe A and B together. What is the total time taken in the whole process?
Answer:
6 am, pipe C is opened to empty \(\frac{1}{2}\) filled tank
Time to empty = 10 hours
Time for cleaning = 1 hour
Part of tank filled by pipes A and B in 1 hour = \(\frac{1}{2}\)
= \(\frac{3}{20}\)^th tank
⇒ time taken to fill the tank completely = \(\frac{20}{3}\) hours
Total time taken in the process = 10 + 1 + \(\frac{20}{3}\)
= 17 hour 40 minutes

(iii) On a given day, pipes A, B and C are opened (in order) at 5 am, 8 am and 9 am respectively, to fill the empty tank. In how many hours will the tank be filled completely?
Answer:
Let the tank be completely filled in ‘t’ hours
⇒ pipe A is opened for ‘t’ hours
pipe B is opened for ‘t – 3’ hours
And, pipe C is opened for ‘t – 4’ hours
⇒ In one hour, part of tank filled by pipe A = \(\frac{t}{15}\)
part of tank filled by pipe B = \(\frac{t-3}{15}\)
and, part of tank emptied by pipe C = \(\frac{t-4}{15}\)
Therefore \(\frac{t}{15}+\frac{t-3}{12}-\frac{t-4}{20}\) = 1
⇒ t = 10.5
Total time to fill the tank = lo hours 30 minutes.

CASE STUDY – II

Question 37.
Mr. Rama Roy a owner of a factory lives in Karnataka. In his factory, he manufacturers razor blades. There is a small chance that \(\frac{1}{500}\) for any bade to be defective.. The blades are in the packet of 10.

Based on the above information, answer the questions given below.

(i) Find the probability that packet contain no defective blade.
Answer:
Here, given N = 1000,
n = 10,
p = \(\frac{1}{500}\) = 0.002
⇒ m = np = 10 × 0.002
⇒ m = 0.02
P(No defective blade) = P(X = 0)
= e^-0.02 (0.002)⁰
= e^-0.02

(ii) The probability that packet contain one defective blade.
Answer:
P(one defective blade) = P(X = 1)
= \(\frac{e^{-0.02}(0.02)^1}{1 !}\)
= 0.02e^-0.02

(iii) Find the probability that packet contain two defective blade, when it is given that e^-0.02 = 0.9802. Also, find the approximate number of packets containing no defective blade, when there are 10000 packets in a consignment. (Use e^-0.02 = 0.9802)
Answer:
P(two defective blade) = P(X = 2)
= \(\frac{e^{-0.02}(0.02)^2}{2 !}\)
= \(\frac{0.9802 \times 0.0004}{2}\)
= 0.000196
= 0.0002
P (no defective blade) = e^-0.02 = 0.9802
So, the approximate number of packets containing no defective blade
= 10,000 × 0.9802 = 9802

OR

Find the approximate number of packets containing one defective blade, when there are 20,000 packets in the consignment. (use e^-0.02 = 0.9802)
Answer:
∵ P(one defective blade) = 0.02e^-0.02
= 0.02 × 0.9802
= 0.0196
So, the approximate number of packets containing defective blade = 20,000 × 0.0196 = 392.

CASE STUDY – III

Question 38.
When observed over a long period of time, a time series data can predict trend that can forecast increase or decrease or stagnation of a variable under consideration. Such analytical studies can benefit a business for forecasting or production of future estimated sales or production.

Mathematically, for finding a line of best-fit to represent a trend, many methods are available. Methods like moving averages and least-squares are some of the techniques to predict such trends.

Mrs. Shamita runs a bread factory and the record of her sales of bakery items for the period of 2015-2019 is as follows:

By taking year 2017 as original, use method of least-squares to find the best-fit trend line equation for Mrs. Shamita’s business. Show the steps of your working.
What are the estimated sales for Mrs. Shamita’s business for year 2022?
Answer:

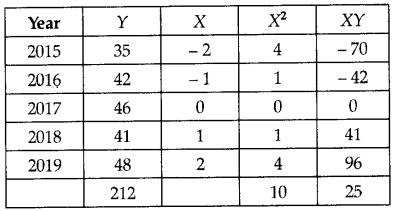
a = \(\frac{\Sigma Y}{n}\)
= \(\frac{212}{5}\)
= 42.4
b = \(\frac{\sum X Y}{\Sigma X^2}\)
= \(\frac{25}{10}\)
= 2.5
Y_C = 42.4 + 2.5X
For year 2022,
Y₂₀₂₂ = 42.4 + 2.5 (2022 – 2017)
= 54.9

OR

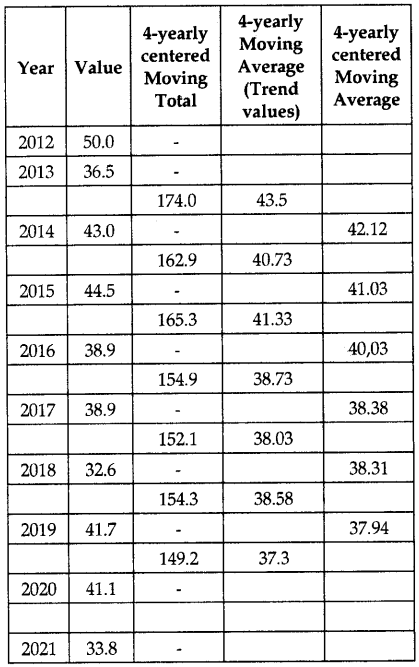
From the following data calculate the 4-yearly moving averages and determine the trend values.

Answer:
Calculation of trend values by it four yearly moving averages: