CBSE Sample Papers for Class 11 Physics Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 11 Physics with Solutions and marking scheme Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Physics Set 1 with Solutions

Time Allowed : 3 hours
Maximum Marks : 70

General Instructions:

1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections: Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary

• c = 3 × 10⁸ m/s
• me = 9.1 × 10^-31 kg
• µ₀ = 4π × 10^-7 TmA^-1
• ε₀ = 8.854 × 10^-12 × C² N^-1 m^-2
• Avogadro’s number = 6.023 × 10²³ per gram mole

Section – A

Question 1.
The number of significant figure in 2.64 × 10²⁴ is
(A) 1
(B) 7
(C) 3
(D) 5
Answer:
(C) 3

Question 2.
The numbers 2.545 and 2.535 on rounding off to 3 significant figures will give
(A) 2.55 and 2.54
(B) 2.54 and 2.53
(C) 2.55 and 2.53
(D) 2.54 and 2.54
Answer
(D) 2.54 and 2.54

Question 3.
Which of the following statement is incorrect?
(A) Speed and velocity are vector quantities
(B) Speed and density are scalar quantities
(C) Displacement and velocity are vector quantities
(D) Mass and density are scalar quantities
Answer:
(A) Speed and velocity are vector quantities

Question 4.
A girl runs 10 m towards south and then 20 m towards west. The displacement is
(A) 22.4 m
(B) 30 m
(C) 10 m
(D) 20 m
Answer:
(A) 22.4 m

Explanation:
Displacement = \(\sqrt{10^2+20^2}\)
= \(\sqrt{100+400}\)
= \(\sqrt{500}\)
= 22.36

Question 5.
Velocity-time graph of a particle projected vertically upward is a
(A) Straight line
(B) Parabolic
(C) Circular
(D) Exponential
Answer:
(A) Straight line

Explanation:
Acceleration acting on the particle is g which is a constant. So, the slope of v-t graph will be constant i.e., the graph will be a straight line.

Question 6.
A stone is dropped from a running train. The stone will hit the ground following a
(A) Straight path
(B) Circular path
(C) Parabolic path
(D) None of these
Answer:
(C) Parabolic path

Explanation:
When dropped from the running train the stone will move horizontally with the same velocity due to inertia. The force of gravity will act on it downward. Hence, the stone will follow a parabolic path.

Question 7.
The distances of planet 1 and planet 2 from sun is 1013 m and 1012 m. If they move in circular orbits then the ratio of their time period is
(A) 10 \(\sqrt{10}\)
(B) 10
(Q \(\sqrt{10}\)
(D) \(\frac{1}{\sqrt{10}}\)
Answer:
(A) 10 \(\sqrt{10}\)

Explanation:
\(\frac{\mathrm{T}_2}{\mathrm{~T}_2}=\left(\frac{d_2}{d_2}\right)^{3 / 2}\)
\(\frac{\mathrm{T}_1}{\mathrm{~T}_2}=\left(\frac{10^{13}}{10^{12}}\right)^{3 / 2}\)
\(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\) = 10^3/2
∴ \(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\) = 1000 = 10 \(\sqrt{10}\)

Question 8.
Bernoulli’s principle is based on principle of conservation of __________
(A) Energy
(B) Mass
(C) Linear momentum
(D) Angular momentum
Answer:
(A) Energy

Question 9.
When temperature of water decreases from 4°C to 0°C its density _________, volume _________.
(A) Increases, increases
(B) Decreases, decreases
(C) Increases, decreases
(D) Decreases, increases
Answer:
(D) Decreases, increases

Explanation:
Due to anomalous expansion of water if the temperature of water decreases from 4°C to 0°C its density decreases, volume increases.

Question 10.
An ideal gas is in chamber A of volume V and absolute temperature T. It is allowed to rush freely into chamber B of volume V which was initially vacuum. The whole system is thermally isolated. The final temperature of the system after equilibrium is
(A) \(\frac{T}{4}\)
(B) \(\frac{T}{2}\)
(C) T
(D) 2T
Answer:
(C) T

Explanation:
For free expansion,
∆U = 0
∴ Initial temperature = Final temperature = T

Question 11.
A particle moves such that its acceleration a is given by a = – bx, where x is the displacement from equilibrium position and b is a constant. The period of oscillation is
(A) \(\frac{2 \pi}{\sqrt{b}}\)
(B) \(\frac{\sqrt{b}}{2 \pi}\)
(C) \(\frac{2 \pi}{\sqrt{b}}\)
(D) 2πb
Answer:
(A) \(\frac{2 \pi}{\sqrt{b}}\)

Explanation:
Time period = 2π \(\sqrt{\left(\frac{\text { Displacement }}{\text { Acceleration }}\right)}\)
= 2π \(\pi \sqrt{\left(\frac{x}{b x}\right)}\)
= 2π \(\sqrt{\left(\frac{1}{b}\right)}\)
= \(\frac{2 \pi}{\sqrt{b}}\)

Question 12.
The period of a simple pendulum will be doubled when its length
(A) Is halved
(B) Is doubled
(C) Is made 4 times
(D) Is made one fourth
Answer:
(C) Is made 4 times

Explanation:
Initially,
T = 2π \(\sqrt{\frac{I}{g}}\)
Finally,
2T = 2π \(\sqrt{\frac{I}{g}}\)
or, \(2 \times 2 \pi \sqrt{\frac{I}{g}}=2 \pi \sqrt{\frac{I}{g}}\)
or, \(\frac{4 I}{g}=\frac{I}{g}\)
∴ l’ = 4l

For Questions 13 to 16 two statements are given — one labelled Assertion (A) and other labelled Reason (R). Select the correct answer to these questions from the options as given below.
(A) If both Assertion and Reason are true and Reason is correct explanation of Assertion.
(B) if both Assertion and Reason are true and Reason is not the correct explanation of Assertion.
(C) If Assertion is true but Reason is false.
(D) if both Assertion and Reason are false.

Section – B

Question 13.
Assertion (A) : The time period of a pendulum is given by T = kqJ.
Reason (R) : The value of the constant k can be determined by dimensional analysis.
Answer:
(C) If Assertion is true but Reason is false.

Explanation:
Time period of a pendulum is given by
T = k \(\sqrt{\left(\frac{l}{g}\right)}\)
= 2π \(\sqrt{\left(\frac{l}{g}\right)}\)
Hence, the assertion is true.
The value of the constant k cannot be determined by dimensional analysis. This is a limitation of dimensional analysis.
Hence, the reason is false.

Question 14.
Assertion(A) : When displacement of a moving particle is zero, then the distance covered by it is not zero.
Reason(R) : Displacement is a vector quantity and distance is a scalar quantity.
Answer:
(A) If both Assertion and Reason are true and Reason is correct explanation of Assertion.

Explanation:
When a particle returns to its starting point then its displacement is zero. But the distance covered by it not zero. Hence, the assertion is true. Displacement is a vector quantity and distance is a scalar quantity. Hence, displacement can be zero but distance covered cannot be zero for a moving particle. Hence, the reason is also true and explains the assertion.

Question 15.
Assertion (A) : One of the simplest periodic functions is f(t) = A cos ωt.
Reason (R) : If the argument of A cos « is increased by an integral multiple of 2π radians, the value of the function remains the same.
Answer:
(A) If both Assertion and Reason are true and Reason is correct explanation of Assertion.

Explanation:
The function that repeats itself at regular intervals of time is called periodic function.
A cos 0° = A cos 2π
= A cos 4π ………………….
Hence, the value of A cos ot repeats as the argument is increased by an integral multiple of 2it radians.
Hence, A cos Lot is a periodic function.
So, the assertion and reason both are true and the reason explains the assertion.

Question 16.
Assertion (A) : Beats are audible when two vibrating tuning forks of fre4uency 1024 Hz and 2048 Hz are brought closer.
Reason (R) : Beats are clearly audible if the difference of frequencies of the two waves is more than 1000 Hz.
Answer:
(D) if both Assertion and Reason are false.

Explanation:
Beats are not audible when two vibrating tuning forks of frequency 1024 Hz and 2048 Hz are brought closer since to hear the beats clearly the difference of frequencies of the two waves should be less than 10 Hz. So, assertion and reason both are false.

Question 17.
Derive S.I. unit of Joule 0) in terms of fundamental units.
Answer:
Joule is a unit of work.
Using the relation,
Work = force × displacement
= mass × acceleration × displacement
= mass × \(\frac{\text { velocity }}{\text { time }}\) × displacement
= mass × \(\frac{\text { displacement }}{\text { time } \times \text { time }}\) × displacement
= mass × displacement² × time^-2
Unit of work,
J = kg × m² × s^-2
= kgm²s^-2.

Question 18.
When a man jumps out of a boat, then it is pushed away. Why?
Answer:
This is due to the Newton’s third law of motion. When the man jumps out of the boat, he applies a force on it in the backward direction and in turn, the reaction of the boat on the man pushes him out of the boat.

Question 19.
Is kinetic energy a scalar or a vector ? Give its S.I. unit and dimensional formula.
Answer:
Kinetic energy is a scalar.
S.I. unit of kinetic energy is joule (J).
Dimensional formula of kinetic energy is [ML²T^-2].

Question 20.
Give an expression for work done in rotational motion in terms of torque.
Answer:
Work done in rotational motion,
W = ΣF_i r_i × ∆θ
where ΣF_i r_i is the algebraic sum of moment of forces and ∆θ is the angle through which a body is rotated,
∴ W = Total torque × Angular displacement

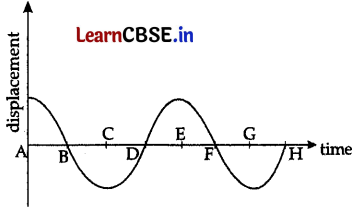
Question 21.
Displacement versus time curve for a particle executing S.H.M. is shown in Fig. Identify the points where
(i) velocity of the oscillator is zero,
(ii) speed of the particle is maximum.

Answer:
(i) Velocity of the particle is zero at A, C, E and G.

(ii) Speed of particle is maximum is at B, D, F and H.

OR

Displacement versus time curve of a particle executing S.H.M. is shown in fig. Find maximum velocity of the particle.

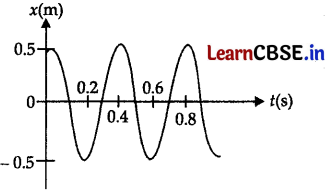
Answer:
v_max = aω
or, v_max = a × \(\frac{2 \pi}{T}\)
or, v_max = 0.5 × \(\frac{2 \pi}{0.4}\)
∴ v_max = 2.5π

Section – C

Question 22.
(a) If both the speed of a body and radius of its circular path are doubled, what will happen to the centripetal acceleration ?
Answer:
Centripetal acceleration
a = v²/r
When v’ = 2v
and r’ = 2r,
then a’ = v’²/r’
= (2v)² / (2r) = 2a

(b)What is the angle between velocity vector and acceleration vector in uniform circular motion ?
Answer:
90°

Question 23.
(a) Sometimes we need to increase friction. Why ?
Answer:
Sometimes friction between two surfaces decreases to such an extent that it is difficult to move on that surface. So, friction needs to be increased. For example, vehicles can’t move on a road covered with snow. In such cases we have to throw sand on the road to increase the friction.

(b) Why banking of road at turnings is required ?
Answer:
Banking of road at turnings is require to provide the necessary centripetal force to avoid the chance of skid.

Question 24.
(a) Prove work energy theorem for a variable force.
(b) Why do spring balances show wrong readings after they have been used for a long time?
Answer:
Using the relation for kinetic energy,
K.E. = \(\frac {1}{2}\) mv²
We get rate of change of K.E. with respect to time as
\(\frac{d}{d t}\) (K.E.) = \(\frac{d}{d t}\) [\(\frac {1}{2}\) mv²]
= \(\frac {1}{2}\) × m × 2 × v × \(\frac{d v}{d t}\)
= mv \(\frac{d v}{d t}\)
But \(\frac{m d v}{d t}\) = ma = F
where a is acceleration and F is force.
∴ \(\frac{d}{d t}\) K.E. = Fv = F \(\frac{d x}{d t}\)
or d (K.E.) = F dx
Integrating between the initial and final energies, i.e., K.E._i. and K.E._f and also position, i.e., x_i and x_f respectively, we get
\(\int_{K . E_{\cdot_i}}^{K \cdot E_{\cdot_f}}\) d(K.E.) = \(\int_{x_i}^{x_f}\) F dx
∴ K.E._(f) – K.E._(i) = W
The work energy theorem is thus verified for variable force.

Question 26.
(a) State second law of thermodynamics.
(b) What is a diathermic material ?
Answer:
(a) (b) is more brittle. A material is said to be brittle if there is small stress-strain variation beyond elastic point and fracture point of brittle material lies close to elastic point.

(b) This happens due to elastic fatigue in spring.

Question 27.
(a) On the basis of kinetic theory of gases, explain, how does a gas exert pressure ?
(b) What do you mean by mean free path of a gas molecule ?
Answer:
(a) According to kinetic theory, the molecules of a gas are in a state of continuous random motion. They collide with one another and also with the walls of the vessel.

Whenever a molecule collides with the wall, it returns with a changed momentum and an equal momentum is transferred to the wall and thus creating pressure.

(b) The mean free path of a gas molecule is the average distance travelled by the molecule between its two successive collisions with other molecules.

Question 28.
(a) When will the motion of a simple pendulum be simple harmonic?
(b) What is the phase difference between velocity and displacement when a particle is executing S.H.M. ?
Answer:
(a) The motion of a simple pendulum will be simple harmonic when the bob is displaced from mean position in such a way that sin θ ≈ θ

(b) Displacement, y = A sin ωt
Velocity = v = \(\frac{d y}{d t}\)
= Aω cos ωt
= Aω sin (ωt + \(\frac{\pi}{2}\))
∴ phase difference between y and v is
∆Φ = {(ωt + \(\frac{\pi}{2}\)) – ωt} = \(\frac{\pi}{2}\)

OR

(a) Draw a graph to show the variation of P.E., K.E. and total energy of a simple harmonic oscillator with displacement.
(b) What is the ratio of maximum acceleration to the maximum velocity of a simple harmonic oscillator?
Answer:
(a)

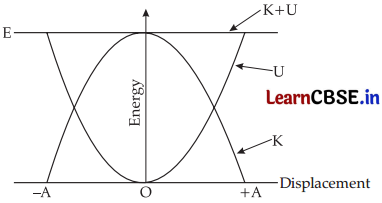
E = K + U = constant

(b) \(\frac{a_{\max }}{v_{\max }}=\frac{\omega^2 A}{\omega A}\) = ω

Section – D

Question 29.
Read the following text and answer the following questions on the basis of the same:

In a uniform gravitational field, the centre of mass coincide with the centre of gravity. But these two points do not always coincide, however. For example, the Moon’s centre of mass is very close to its geometric centre (it is not exact because the Moon is not a perfect uniform sphere), but its centre of gravity is slightly displaced towards Earth because of the stronger gravitational force on the Moon’s near side facing the earth.

If an object does not have a uniform weight distribution then the centre of mass will be closer to where most of the weight is located. For example, the centre of mass for a hammer is located close to where the head connects to the handle.

The centre of mass can be located at an empty point in space, such as the centre of a hollow ball.
The centre of mass can even be completely outside of an object, such as for a donut or a curved banana.

Standing upright, an adult human’s centre of gravity is located roughly at the center of their torso. The centre of gravity rises a few inches when with rising arms.
The center of gravity can even be at a point outside the body, such as when bent over in an inverted-U pose.

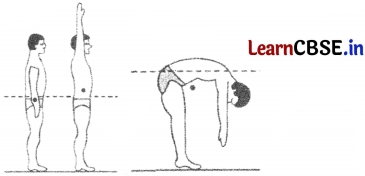
An object is in a balanced position if its center of mass is above its base of support. For the two cylinders below, the left cylinder’s center of gravity is above the base of support so the upward support force from the base is aligned with the downward force of gravity. For the cylinder on the right, the center of gravity is not above the base of support so these two forces cannot align and instead create a torque that rotates the object, tipping it over.

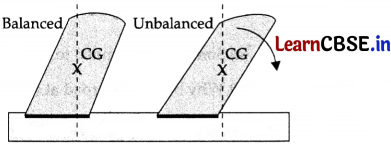
(i) Does the centre of mass not coincide with the centre of gravity of a body?
(A) No. These two points do not coincide when the body is placed in high viscous medium
(B) No. These two points do not coincide when the body is placed in a strong magnetic field
(C) No. These two points do not coincide when the body is placed in a non-uniform gravitational field
(D) Yes. These two points always coincide
Answer:
(C) No. These two points do not coincide when the body is placed in a non-uniform gravitational field

Explanation:
In a uniform gravitational field, the centre of mass coincide with the center of gravity.

(ii) Two similar blocks are shown below. The first block is top-heavy and the second block is bottom-heavy. Where the centers of mass will be located?

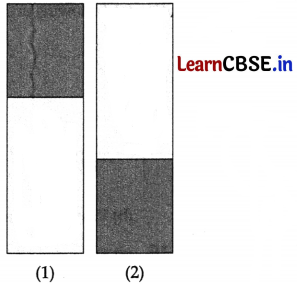
(A) At the centre of both the blocks
(B) Above the geometrical centre for block 1 and below the geometrical centre for block 2
(C) Above the geometrical centre for block 2 and below the geometrical centre for block 1
(D) Above the geometrical centre for both the blocks
Answer:
(B) Above the geometrical centre for block 1 and below the geometrical centre for block 2

Explanation:
If an object does not have a uniform weight distribution then the center of mass will be closer to where most of the weight is located.

(iii) Identical blocks are connected as shown. Where the center of mass is expected to be located?

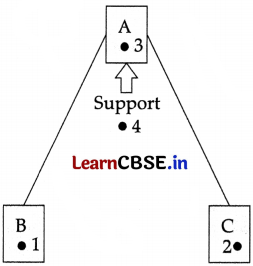
(A) At point 1
(B) At point 2
(C) At point 3
(D) At point 4
Answer:
(D) At point 4

Explanation:
Since, all the 3 blocks are identical, the centre of mass will be below the support but above the line joining the blocks B and C.

Or

Identical blocks are connected as shown. Where the center of mass is expected to be located?
(A) At point 1
(B) At point 2
(C) At point 3
(D) At point 4
Answer:
(A) At point 1

Explanation:
The Leaning Tower of Pisa does not fall because its center of mass has been carefully kept within its base.
Today, despite the inclination of about 40 (reduced from over 50), a vertical line drawn from the center of mass still falls inside the base.

(iv) The leaning tower of Pisa does not fall since
(A) Its centre of mass is within its base
(B) Its center of mass is at the foot of the perpendicular dropped from the top.
(C) Its center of mass coincides with its centre of gravity.
(D) Its base is well concreted
Answer:
(B) Its center of mass is at the foot of the perpendicular dropped from the top.

Explanation:
The Moon’s centre of mass is very close to its geometric centre (it is not exact because the Moon is not a perfect uniform sphere), but its centre of gravity is slightly displaced towards Earth due to uneven gravitational field. The gravitational force is stronger on the Moon’s near side facing the earth.

Question 30.
Read the following text and answer the following questions on the basis of the same:

Expansion and contraction of steel and concrete structure due to seasonal heating and cooling is a common problem found in civil engineering. To combat this problem, engineers put expansion joints to absorb these changes.

This problem is compounded on railway tracks. This could lead to rail buckling, known in the industry as “Sun kink”, as shown below, and cause the derailment of train.

When exposed to temperature variations, the rail tends to vary its length. If this tendency is freely allowed, for a temperature variance
At, the rail length L will vary by ∆L. This length variance can be computed as:
∆L = αL∆t
where α = expansion coefficient of steel = 11.5 × 10^-6 /°C.

The coefficient of thermal expansion is defined as the fractional increase in length per unit rise in temperature.
Traditional railway tracks are of standard lengths. When the tracks are laid, the lengths are joined end to end using “fishplates”—short lengths of steel plate overlapping the joint, and bolted to the ends of the rails.

At each joint there must be a short gap (≈ 1/8″) between the rail ends, to allow for longitudinal thermal expansion of the rails on hot days.

(i) “Sun kink” is the
(A) Buckling of railway tracks due to seasonal heating and cooling.
(B) Fracture of railway tracks due to seasonal heating and cooling.
(C) Buckling of railway track arising from the high pressure of loaded wagons.
(D) None of the above.
Answer:
(A) Buckling of railway tracks due to seasonal heating and cooling.

Explanation:
Expansion and contraction of steel and concrete structure due to seasonal heating and cooling is a common problem found in civil engineering.
This problem is predominant on railway tracks. This could lead to rail buckling, known in the industry as “Sun kink”, and cause the derailment of train.

(ii) What is the value of thermal expansion coefficient of steel?
(A) 1.15 × 10^-6 /°C
(B) 0.115 × 10^-6 /°C
(C) 11.5 × 10^-6 /°C
(D) 11.5 × 10⁶ /°C
Answer:
(C) 11.5 × 10^-6 /°C

Explanation:
Expansion coefficient of steel = 11.5 × 10^-6 /°C

(iii) What will be the expansion of a 20 m long railway steel track for 30°C variation of temperature?
(A) 6.9 m
(B) 6.9 cm
(C) 6.9 mm
(D) 0.69 m
Answer:
(C) 6.9 mm

Explanation:
∆L = αL∆t
α = 11.5 × 10^-6 /°C
L = 20 m
∆t = 30°C
Putting the values in the expression:
∆L = 11.5 × 10^-6 × 20 × 30 = 6.9 mm

(iv) At each railway track joint a short gap of (approximately) is left.
(A) 1/8 mm
(B) 1/8 cm
(C) 1/8 m
(D) 1/8 inch
Answer:
(D) 1/8 inch

Explanation:
At each joint of railway track there must be a short gap (≈ 1/8”) between the rail ends, to allow for longitudinal thermal expansion of the rails on hot days.

OR

Which of the following statement is true?
(A) Expansion joint maintain 1/8″ gap whatever be the temperature change.
(B) Expansion joint increases when temperature decreases and decreases when temperature increases.
(C) Expansion joint decreases when temperature decreases and increases when temperature increases.
(D) Expansion joints expands with the rise of temperature.
Answer:
(B) Expansion joint increases when temperature decreases and decreases when temperature increases.

Explanation:
Normally 1/8″ gap is left when two railway track ends are joined with fishplate. When temperature rises, the rail tracks expand and this gap accommodates the expansion of the steel track. So, the gap contracts. When temperature decreases, the rail tracks contract and this gap increases.

Section – E

Question 31.
(a) In the case of rocket propulsion derive expression for
(i) Velocity of rocket at any instant,
(ii) Thrust on the rocket,
(iii) Speed of the rocket when whole fuel is burnt.
Answer:
(a) At time t = 0
Let the mass of rocket with fuel = m₀
Velocity of the rocket with respect to earth = v₀
At time t = t
Mass of rocket with fuel = m
and velocity of rocket w.r.t. earth = v
such that m < m₀ and v > v₀
At time (t + dt)
If at time (t + dt), the mass of fuel burnt is din which gives gases of velocity V_g and velocity of rocket becomes (v + dv).
Using the law of conservation of momentum
mv = (m – dm) (v + dv) – dmv_g
(v_g is with — ve sign because it acts downward)
i.e., mdv = – (v_g + v) dm
(neglecting dmdv being very small)
i.e., mdv = – udm
(u is the relative velocity of gases with respect to the rocket)

(i) Velocity of rocket at any instant
Using mdv = – udm
(∵ velocity increase with decrease in mass)
Integrating
\(\int_{v_0}^v d v=-\int_{m_0}^m u \frac{d m}{m}=u \int_{m_0}^m \frac{d m}{m}\)
i.e., v – v₀ = – u [log_e m – log_e m₀]
= u [log_e m₀ – log_e m]
i.e., v = v₀ + u log_e \(\frac{m_0}{m}\)
If v₀ = 0,
v = u log_e \(\frac{m_0}{m}\)

(ii) Thrust on the rocket
Using, mdv = – u dm,
(neglecting ‘-‘ ve sign because it only represents direction)
we get,
\(\frac{m d v}{d t}=u \frac{d m}{d t}\)
(dividing both sides by dt)
or m × a = u \(\frac{d m}{d t}\)
(where acceleration, a = \(\frac{d v}{d t}\))
or F = \(\frac{u d m}{d t}\)

(iii) Speed of the rocket when whole fuel is burnt
Using, v = v₀ + u log_e \(\frac{m_0}{m}\)
where, v = v_e, speed of empty rocket
and m = m_e, mass of empty rocket
we get, v_e = v₀ + u log_e \(\frac{m_0}{m}\)

(b) Why Newton’s second law of motion is not applicable to the motion of a rocket ?
Answer:
Newton’s second law, i.e., \(\vec{F}=m \vec{a}\) is applicable only if the mass (m) of the body remains constant. In case of the rocket, the mass continuously decreases and hence \(\vec{F}=m \vec{a}\) is not applicable.

OR

(a) What is pseudo force ?
Answer:
The fictitious or imaginary force used to balance an actual or material force is called pseudo force,
e.g., centrifugal force, F = \(\frac{-m v^2}{r}\) is a pseudo force.
Pseudo forces do not have material sources, they are simply produced because of the acceleration or rotation of the frame itself.

(b) Why automobiles tyres have generally irregular projections over their surface ?
Answer:
The automobile tyres have generally irregular
projections over their surface so as to:
(i) Increase friction,
(ii) Increase the grip with the the ground and thus avoiding their skidding.

(c) Is force of friction independent of path ?
Answer:
No, the frictional force is a non-conservative force, i.e., the work done by it depends upon the actual path followed by a body.

Question 32.
(a) A dog of mass 10 kg is standing on a flat 10 m long boat so that it is 20 meters from the shore. It walks 8 m on the boat towards the shore and then stops. The mass of the boat is 40 kg and friction between the boat and the water surface is negligible. How far is the dog from the shore now?

Answer:
We consider boat and dog as a system. Initially, centre of mass of the system is at rest. Since, no external force is acting on the system, hence centre of mass of the system will remain stationary. Let initially distance of the centre of mass of the boat from the shore be x_{1 cm} m.
Then, x_{1 cm} = \(\left(\frac{40 \times x+10 \times 20}{40+10}\right)\) m
Here, x_{1 cm} = distance of the C.M. of the system from the shore.
Since, dog moves towards the shore, for the centre of mass of the system to be at rest, the boat has to move away from the shore.
Let distance moved by the boat be ‘x’. Then,
x_{2 cm} = \(\left(\frac{40\left(x+x^{\prime}\right)+10\left(20-8+x^{\prime}\right)}{40+10}\right)\)
AS x_{1 cm} = x_{2 cm}
⇒ 50x’ = 80
⇒ x’ = 16 m.
Hence, distance of dog from the shore is (20 – 8 + 1.6) m = 13.6 m.

(b) Two solid wooden balls roll down two different inclined planes of different inclination but same height. Comment upon their speed and time of descent ?
Answer:
It will reach the bottom with same speed in each case because speed depends upon height and not in inclination.
It will take longer to roll down on the plane with smaller inclination.

OR

(a) There are two spheres of same mass and radius one is solid and the other is hollow. Which of them has a larger moment of inertia about its diameter ?
Answer:
The hollow sphere shall have greater M.L, as its entire mass is concentrated at the boundary of the sphere at maximum distance from the axis.

(b) Using the expression for power and K.E. of rotation motion, derive the relation τ = Iα.
Answer:
We know that power is given by
P = τω ………….(1)
Also we know that,
K.E. = \(\frac {1}{2}\) Iω² …………..(2)
As P = rate of change of energy
= rate of change of K.E.
= \(\frac{d}{d t}\left(\frac{1}{2} I \omega^2\right)\)
= \(\frac {1}{2}\) × I × 2ω \(\frac{d \omega}{d t}\)
= Iwα
(∵ \(\frac{d \omega}{d t}\) = α) …………….(3)
∴ From equation (1) and (3), we get
P = τω
Since τ = Iα.

(c) Is radius of gyration of a body is a constant quantity ?
Answer:
No, radius of gyration of a body depends on axis of rotation and also on distribution of mass of the body about this axis.

Question 33.
(i) The stress-strain graph for a metal wire is given in figure. Upto the point B, the wire returns to its original state O along the curve BAO, when it is gradually unloaded. Point E corresponds to the fracture point of the wire.

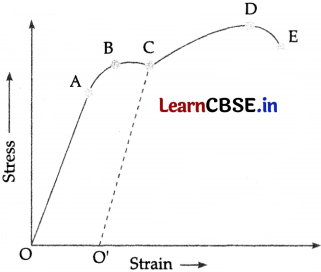
(A) Upto which point of curve, is Hooke’s law obeyed ? This point is also called Proportion limit’.
(B) Which point on the curve corresponds to elastic limit and yield point of the wire?
(C) Indicate the elastic and plastic regions of the stress-strain curve.
(D) What change happens when the wire is loaded upto a stress corresponding to point C on curve, and then unloaded gradually ?
Answer:
(a)Upto point A, Hooke’s law is obeyed because the graph is straight line from O to A.

(b) Point B. From the graph it is clear that the wire returns to its original position after being unloaded upto point B only, hence B is elastic limit.

(c) Elastic region – O to B
Plastic region – B to E

(d) Strain is directly proportional to load upto point A and after A, strain increases by greater amount as compared to first case (i.e., O to A) for a given increase in load. Beyond the elastic limit B, the curve does not retrace backwards as the wire is unloaded but returns along dotted line CO’. Point O’ corresponds to strain at zero load, which shows there is a permanent strain in the wire.

(ii) A silica glass rod has a diameter of 1 cm and is 10 cm long. Estimate the largest mass that can be hung from it without breaking it. (Breaking strength of glass is 50 × 10⁶ Nm².)
Answer:
Using Stress = \(\frac {F}{A}\),
we get F = Stress × A
= (50 × 10⁶) × π × \(\left(\frac{10^{-2}}{2}\right)^2\) N
Largest mass = \(\frac{F}{g}\)
= \(\frac{\left(50 \times 10^6\right)\left(\frac{\pi \times 10^{-4}}{4}\right)}{10}\) kg
= 392.7 kg

(iii) Which is more elastic : Water or air? Give reason.
Answer:
Elasticity is reciprocal of compressibility. Air is more compressive than water. Hence, water is more elastic than air.

OR

(a) Show that a liquid in a state of equilibrium of rest exerts a force perpendicular to the surface only.
Answer:
Let a given quantity of liquid exert force F in a direction θ with the horizontal. Resolving, we get F cos θ along horizontal surface of liquid and F sin θ along the vertical.

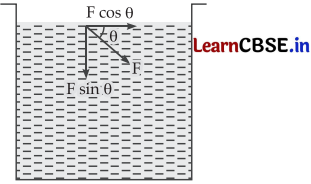
As there is no flow of liquid so F cos θ should be zero.
Since, F ≠ 0, cos θ = 0
or θ = 90°
i.e., a liquid at rest exerts normal force to the walls of the container.

(b) If a small ping-pong ball is placed in a vertical jet of water or air, it will rise to a certain height above the nozzle and stay at that level. Explain.
Answer:
Due to the high velocity of the jet of water, the pressure between the ball and jet decreases. The greater (atmospheric) pressure on the other side of the ball pushes it against the jet and the ball remains suspended. The high velocity of water takes the ball upwards along with it and makes it to spin.

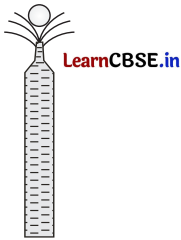
A ping-pong ball supported on a jet of water.

(c) The dams of water reservoir are made thick near the bottom. Why ?
Answer:
Pressure exerted by a liquid column of height h, P = hρg.
As h is large, so P is quite large. Due to it the bottom are made thick.