CBSE Sample Papers for Class 11 Maths Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 11 Maths with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Maths Set 4 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
• Section A has 18 MCQ’s and 2 Assertion-Reason based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA)-type questions of 2 marks each.
• Section C has 6 Short Answer (SA)-type questions of 3 marks each.
• Section D has 4 Long Answer (LA)-type questions of 5 marks each.
• Section Ehas3 source based/case based/passage based/integrated units of assessment of 4 marks each with sub-parts.

Section-A

(Multiple Choice Questions) Each question carries 1 mark

Question 1.
Which of the following is not correct?
(A) sin θ = \(-\frac{1}{5}\)
(B) cos θ = 1
(C) sec θ = \(\frac{1}{2}\)
(D) tan θ = 20
Answer:
(C) sec θ = \(\frac{1}{2}\)
Explanation:
We know that, -1 ≤ sin θ ≤ 1
Therefore, option (A) is correct.
cos θ = 1 is correct as cos 0° = 1
i.e, option (B) is correct.
Given, sec θ = \(\frac{1}{2}\)
⇒ cos θ = 2
Which is incorrect as -1 ≤ cos θ ≤ 1.

Question 2.
The complex number z which satisfies the condition \(\left|\frac{i+z}{i-z}\right|\) = 1 lies on
(A) circle x² + y² = 1
(B) the x-axis
(C) the y-axis
(D) the line x + y = 1
Answer:
(B) the x-axis
Explanation:
We have,

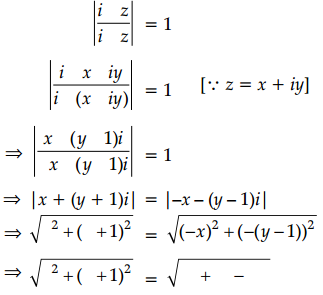
On squaring both sides, we get
⇒ x² + (y + 1)² = x² + (y – 1)²
⇒ x² + (y² + 2y + 1) = x² + (y² – 2y + 1)
⇒ 4y = 0
⇒ y = 0 i.e, x-axis.

Question 3.
If the parabola y² = 4ax passes through the point (3, 2), then the length of its latus rectum is
(A) \(\frac{2}{3}\)
(B) \(\frac{4}{3}\)
(C) \(\frac{1}{3}\)
(D) 4
Answer:
(B) \(\frac{4}{3}\)
Explanation:
Given equation of parabola, y² = 4ax
Since, it passes through (3, 2)
(2)² = 4a × 3
⇒ a = \(\frac{1}{3}\)
Therefore, length of the latus rectum = 4a
= 4 × \(\frac{1}{3}\)
= \(\frac{4}{3}\)

Question 4.
The locus of a point for which x = 0 is
(A) XY-plane
(B) YZ-plane
(C) ZX-plane
(D) None of these
Answer:
(B) YZ-plane
Explanation:
Locus of a point for when x = 0 is YZ plane because on YZ plane, x = 0.

Question 5.
The value of \(\cot \left(\frac{\pi}{4}+\theta\right) \cot \left(\frac{\pi}{4}-\theta\right)\) is
(A) -1
(B) 0
(C) 1
(D) Not defined
Answer:
(C) 1
Explanation:

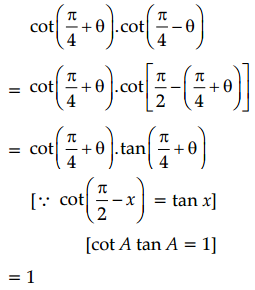
Question 6.
\(\lim _{x \rightarrow 0} \frac{|\sin x|}{x}\) is equal t0
(A) 1
(B) -1
(C) Does not exist
(D) None of these
Answer:
(C) Does not exist
Explanation:

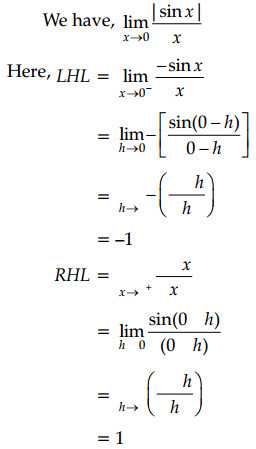
Since, LHL ≠ RHL then limit does not exist.

Question 7.
Solution of a linear inequality in variable x is represented on number line. Choose the correct answer from the given four options.

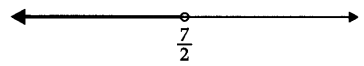
(A) x ∈ (-∞, \(\frac{7}{2}\))
(B) x ∈ (-∞, \(\frac{7}{2}\)]
(C) x ∈ [\(\frac{7}{2}\), -∞)
(D) x ∈ (\(\frac{7}{2}\), ∞)
Answer:
(A) x ∈ (-∞, \(\frac{7}{2}\))
Explanation:
It is clear from the given figure, that all values of x are less than \(\frac{7}{2}\) excluding \(\frac{7}{2}\). i.e. x ∈ (-∞, \(\frac{7}{2}\))

Question 8.
The equation of straight line passing through the point (3, 2) and perpendicular to the line y = x is
(A) x – y = 5
(B) x + y = 5
(C) x + y = 1
(D) x – y = 1
Answer:
(B) x + y = 5
Explanation:
Let required equation of line, l
y – y₁ = m(x – x₁)
As line passes through the point (3, 2).
∴ y – 2 = m(x – 3)
⇒ y = mx + 2 – 3m ……..(i)
Also, given line, l is ⊥r to line y = x
∴ slope of line (l) × slope of line (y = x) = -1
m × 1 = -1
⇒ m = -1
From equation (i), we have
y = -x + 2 + 3
⇒ y = -x + 5
⇒ y + x = 5

Question 9.
If A and B are coefficient of xn in the expansions of (1 + x)²ⁿ and (1 + x)^2n-1 respectively, then \(\frac{A}{B}\) equals
(A) 1
(B) 2
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{n}\)
Answer:
(B) 2
Explanation:
In the expansion of (1 + x)²ⁿ, the the coefficient of xⁿ is ²ⁿC_n
i.e., A = ²ⁿC_n
In the expansion of (1 + x)^2n-1, the coefficient of xⁿ is ^2n-1C_n
i.e., B = ^2n-1C_n

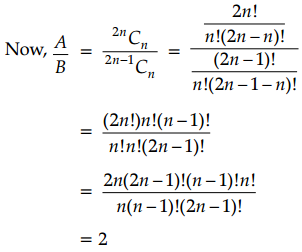
Question 10.
The total number of 9-digit numbers which have all different digits is
(A) 10!
(B) 9!
(C) 9 × 9!
(D) 10 × 10!
Answer:
(C) 9 × 9!
Explanation:
No. of ways of filling

So, required no. of ways = 9 × 9!

Question 11.
If the probabilities for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A or B fails is
(A) > 0.5
(B) 0.5
(C) ≤ 0.5
(D) 0
Answer:
(C) ≤ 0.5
Explanation:
Given, P(A fails) = 0.2, P(B fails) = 0.3
∴ P(either A or B fails) ≤ P(A fails) + P(B fails)
⇒ P(either A or B fails) ≤ 0.2 + 0.3
⇒ P(either A or B fails) ≤ 0.5

Question 12.
The value of sin 50° – sin 70° + sin 10° is equal to
(A) 1
(B) 0
(C) \(\frac{1}{2}\)
(D) 2
Answer:
(B) 0
Explanation:
(sin 50° – sin 70°) + sin 10°
= [2 cos(\(\frac{50^{\circ}+70^{\circ}}{2}\)) sin(\(\frac{50^{\circ}+70^{\circ}}{2}\))] + sin 10°
[∵ sin C – sin D = 2 cos(\(\frac{C + D}{2}\)) sin(\(\frac{C – D}{2}\))
= {(2 cos 60° sin(-10°)} + sin 10°
= -2 cos 60° sin 10° + sin 10°
= -2 × (\(\frac{1}{2}\)) sin 10° + sin 10°
= 0

Question 13.
Let x, y ∈ R, then x + iy is a non-real complex number if
(A) x = 0
(B) y = 0
(C) x ≠ 0
(D) y ≠ 0
Answer:
(D) y ≠ 0
Explanation:
x + iy is a non-zero real complex number if y ≠ 0, when x, y ∈ R

Question 14.
If the coefficient of variation of two distributions are 50, 60 and their arithmetic means are 30 and 25 respectively, then the difference of their standard deviation is
(A) 0
(B) 1
(C) 1.5
(D) 2.5
Answer:
(A) 0
Explanation:
Given, CV₁ = 50, CV₂ = 60, \(\overline{x_1}\) = 30 and \(\overline{x_2}\) = 25

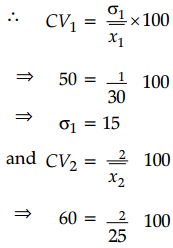
Required difference = σ₂ – σ₁
= 15 – 15
= 0

Question 15.
At what point of the parabola x² = 9y is the abscissa three times that of ordinate?
(A) (1, 1)
(B) (3, 1)
(C) (-3, 1)
(D) (-3, -3)
Answer:
(B) (3, 1)
Explanation:
Given, parabola is x² = 9y
Let P(h, k) be the point on the parabola such that abscissa is 3 times the ordinate.
So, h = 3k ……(i)
Since, P(h, k) lies on the parabola.
So, h² = 9k ……(ii)
From equation (i) and (ii), we get
(3k)² = 9k
⇒ 9k² = 9k
⇒ 9k² – 9k = 0
⇒ 9k(k – 1) = 0
⇒ k = 0, 1
When k = 0, h = 0
So, k = 1
Now, from equation (i), h = 3 × 1 = 3
So, the point is (3, 1).

Question 16.
Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively
(A) 4, 7
(B) 7, 4
(C) 4, 4
(D) 7, 7
Answer:
(B) 7, 4
Explanation:
We know that if a set X contains k elements, then the number of subsets of X are 2^k.
It is given that the number of subsets of a set containing m elements is 112 more than the number of subsets of set containing n elements.
⇒ 2^m – 2ⁿ = 112
⇒ 2ⁿ (2^m-n – 1) = 2 × 2 × 2 × 2 × 7
⇒ 2ⁿ (2^m-n – 1) = 2⁴ (2³ – 1)
⇒ n = 4 and m – n = 3
⇒ m – 4 = 3
⇒ m = 7

Question 17.
If A = {1, 3, 5, 7, 9, 11, 13, 15, 17}, B = {2, 4, 6,…, 18} and N the set of natural numbers is the universal set, then A’ ∪ [(A ∪ B) ∩ B’] is
(A) φ
(B) N
(C) A
(D) B
Answer:
(B) N
Explanation:
A’ ∪ [(A ∪ B) ∩ B’] = A’ ∪ [(A ∩ B’) ∪ (B ∩ B’)]
= A’ ∪ [(A ∩ B’) ∪ φ] = A’ ∪ (A ∩ B’)
= (A’ ∪ A) ∩ (A’ ∪ B’) = N ∩ (A ∩ B)’
= (A ∩ B)’ = φ
= N (Here, Complement of Null Set is N)

Question 18.
When tested, the lives (in hours) of 5 bulbs were noted as follows 1357, 1090, 1666, 1494, 1623. The mean deviation (in hours) from their mean is
(A) 178
(B) 179
(C) 220
(D) 356
Answer:
(A) 178
Explanation:
Mean, \(\bar{x}=\frac{1357+1090+1666+1494+1623}{5}\)
= \(\frac{7230}{5}\)
= 1446

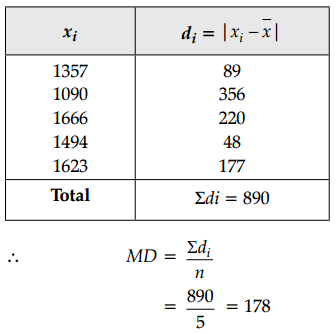
Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(A) Both (A) and (R) are true and (R) is the correct explanation of (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A): If (4x + 3, y) = (3x + 5, -2), then x = 2 and y = -2.
Reason (R): If A = {-1, 3, 4}, then A × A is {(-1, -1), (-1, 3), (-1, 4), (3, -1), (4, -1), (3, 4)}.
Answer:
(C) (A) is true but (R) is false.
Explanation:
Assertion is true, because
If (4x + 3, y) = (3x + 5, -2)
⇒ 4x + 3 = 3x + 5 and y = -2
⇒ x = 2 and y = -2
Reason is false, because
A × A = {-1, 3, 4} × {-1, 3, 4} = {(-1, -1), (-1, 3), (-1, 4), (3, -1), (3, 3), (3, 4), (4, -1), (4, 3), (4, 4)}

Question 20.
Assertion (A): A number of four different digits is formed with the help of the digits 1, 2, 3, 4, 5, 6, 7 in all possible ways. Then, number of ways which are exactly divisible by 4 is 200.
Reason (R): A number divisible by 4, if unit place digit is divisible by 4.
Answer:
(C) (A) is true but (R) is false.
Explanation:
For the number exactly divisible by 4, then last two digits must be divisible by 4, the last two digits are 12, 16, 24, 32, 36, 52, 56, 64, 72, 76.
Total 10 ways.
Now, the remaining two first places on the left of 4-digit numbers are to be filled from the remaining 5-digits and tills can be done in ⁵P₂ = 20 ways.
∴ Required number of ways = 20 × 10 = 200.

Section-B

[This section comprises very short answer-type questions (VSA) of 2 marks each]

Question 21.
If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B
(ii) B ∩ C
OR
If R is the set of real numbers and Q is set of rational numbers, then what is R – Q?
Answer:
(i) A ∩ B = {3, 5, 7, 9, 11} ∩ (7, 9, 11, 13} = {7, 9, 11}
(ii) B ∩ C = {7, 9, 11, 13} ∩ {11, 13, 15} = {11, 13}
OR
R – Q = {set of real number} – {set of rational number}
= {set of rational number + set of irrational number} – {set of rational number}
= set of irrational numbers

Question 22.
Find the range of the following function: f(x) = x² + 2
Answer:
Given, f(x) = x² + 2
Let y = f(x)
⇒ y = x² + 2
⇒ x² = y – 2
⇒ x = \(\sqrt{y-2}\)
Clearly, x will take real values, if
y – 2 ≥ 0
y ≥ 2
∴ Range of y = [2, ∞)

Question 23.
Write the argument of (1 + √3i) (cos θ + i sin θ).
OR
The longest side of a triangle is twice the shortest side and the third side is 2 cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm, then find the minimum length of the shortest side.
Answer:
Let z = (1 + √3i) (cos θ + i sin θ)
= cos θ + √3 sin θ i² + i sin θ + √3i cos θ
= (cos θ – √3 sin θ) + i(sin θ + √3 cos θ)
∴ Re(z) = cos θ – √3 sin θ and Im(z) = (sin θ + √3 cos θ)
Now, argument of z is

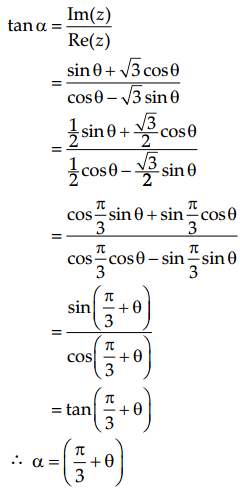
OR
Let the length of shortest side be x cm.
According to the given information,
Longest side = 2 × Shortest side = 2x cm
and third side = 2 + Shortest side = (2 + x) cm
Perimeter of triangle = x + 2x + (x + 2) = 4x + 2
According to the question,
Perimeter > 166 cm
⇒ 4x + 2 > 166
⇒ 4x > 166 – 2
⇒ 4x > 164
⇒ x = 41 cm
Hence, the minimum length of shortest side is more than 41 cm.

Question 24.
Prove that: cos² 2x – cos² 6x = sin 4x sin 8x.
Answer:
L.H.S.= cos² 2x – cos² 6x
= (1 – sin² 2x) – (1 – sin² 6x) (∵ sin²A + cos²A = 1)
= sin² 6x – sin² 2x
= sin(6x + 2x) sin(6x – 2x) [∵ sin²A – sin²B = sin(A + B) sin(A – B)]
= sin 8x sin 4x
= R.H.S.
Hence Proved.

Question 25.
If ⁿC₁₂ = ⁿC₁₃, find the value of ²⁵C_n.
Answer:
Given, ⁿC₁₂ = ⁿC₁₃
⇒ ⁿC_n-12 = ⁿC₁₃ [∵ ⁿC_r = ⁿC_n-r]
⇒ n – 12 = 13
⇒ n = 12 + 13 = 25
Now, ²⁵C₂₅ = \(\frac{25 !}{25 !(25-25) !}\) = 1

Section-C

[This section comprises short answer type questions (SA) of 3 marks each]

Question 26.
Evaluate: \(\lim _{x \rightarrow 0} \frac{e^x-e^{\sin x}}{x-\sin x}\)
Answer:

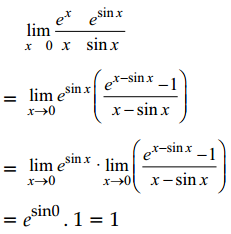
Question 27.
Which of the following pairs of sets are disjoint?
(i) {1, 2, 3, 4} and {x: x is a natural number and 4 ≤ x ≤ 6}
(ii) {a, e, i, o, u} and (c, d, e, f}
(iii) {x: x is an even integer} and {x: x is an odd integer}
Answer:
(i) Let A = (1, 2, 3, 4}
and B = (x: x is a natural number and 4 ≤ x ≤ 6} = (4, 5, 6}
∴ A ∩ B = {4}
Therefore, given sets are not disjoint.
(ii) {a, e, i, o, u} ∩ {c, d, e, f} = {e}
Therefore, given sets are not disjoint.
(iii) (x: x is an even integer} ∩ (x: x is an odd integer}
∴ {2, 4, 6, 8, 10,……} ∩ (1, 3, 5, 7,…..} = φ
Therefore, given sets are disjoint.

Question 28.
Prove that: (cos x + cos y)² + (sin x – sin y)² = \(4 \cos ^2 \frac{x+y}{2}\)
OR
Prove that: cos θ cos\(\frac{\theta}{2}\) – cos 3θ cos\(\frac{9 \theta}{2}\) = sin 7θ sin 8θ
Answer:

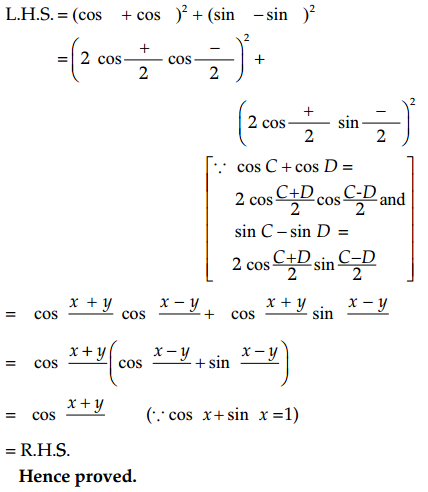
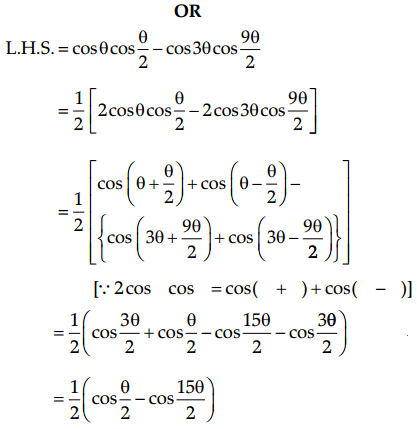
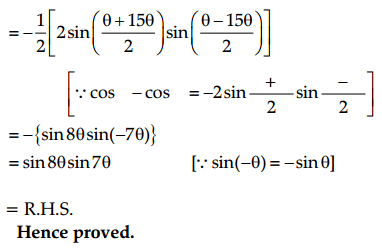
Question 29.
Determine the number of terms in A.P. 3, 7, 11,…. 407. Also, find its 11th term from the end.
OR
Find the least value of n for which 1 + 3 + 3² + …… + 3^n-1 > 1000.
Answer:
Given A.P. is 3, 7, 11,….. 407
Here, a = 3, d = 4, l = 407
Using formula, T_n = l = a + (n – 1)d, we get
407 = 3 + (n – 1)4
⇒ 4n = 408
⇒ n = 102
We need 11th term from the end
Last term = 102th
Second last term = 102 – 1 = 101th
Third last term = 102 – 2 = 100th
and so on
So, 11th term from the end = (102 – 10)term = 92th term
∴ T₉₁ = a + (92 – 1)d
= 3 + 91 × 4
= 3 + 364
= 367
OR
We have, 1 + 3 + 3² + ….. + 3^n-1 > 1000
⇒ 3⁰ + 3¹ + 3² + ….. + 3^n-1 > 1000
⇒ \(3^0\left(\frac{3^n-1}{3-1}\right)\) > 1000
⇒ 3ⁿ – 1 > 2000
⇒ 3ⁿ > 2001
Least value of n, which satisfies this inequality is n = 7 (∵ 3⁷ = 2187)
Hence, least value of n = 7.

Question 30.
Find the equation of the straight line which bisects the distance between the points A(a, b) and B(a’, b’) and also bisects the distance between the points C(-a, b) and D(a’, -b’).
OR
Find the equation of the circle having (1, -2) as its centre and passing through 3x + y = 14, 2x + 5y = 18.
Answer:
Co-ordinate of mid-point of A(a, b), B(a’, b’) are \(\left(\frac{a+a^{\prime}}{2}, \frac{b+b^{\prime}}{2}\right)\), and co-ordinate of mid-point of C(-a, b), D(a’, -b’) are \(\left(\frac{-a+a^{\prime}}{2}, \frac{b-b^{\prime}}{2}\right)\).
Now, the equation of the line passing through (x₁, y₁) and (x₂, y₂) is


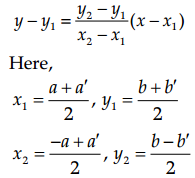
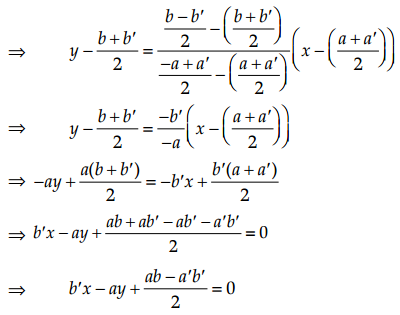
⇒ 2b’x – 2ay + (ab – a’b’) = 0 is the required equation of the line.
OR
Given that, centre of the circle is (1, -2) and the circle passing through the lines
3x + y = 14 …..(i)
and 2x + 5y = 18 …..(ii)
Solving (i) & (ii) we get x = 4 & y = 2
∴ Radius of the circle = \(\sqrt{(4-1)^2+(2+2)^2}\)
= \(\sqrt{9+16}\)
= 5
Now, equation of the circle with centre C(1, -2) and radius, r is 5 is
(x – 1)² + (y + 2)² = 5²
⇒ x² – 2x + 1 + y² + 4y + 4 = 25
⇒ x² + y² – 2x + 4y – 20 = 0

Question 31.
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if a team has
(i) no girl
(ii) at least 3 girls
(iii) at least one girl and one boy?
Answer:
(i) no girl

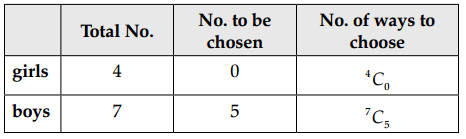
Total number of ways = ⁴C₀ × ⁷C₅

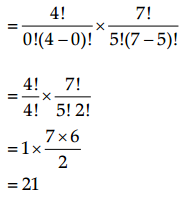
(ii) Since the team has to consist of at least 3 girls, the team can consist of
(a) 3 girls and 2 boys
(b) 4 girls and 1 boy
(a) 3 girls and 2 boys

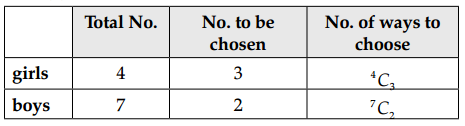
Number of ways selecting = ⁷C₂ × ⁴C₃
= \(\frac{7 !}{2 ! 5 !} \times \frac{4 !}{3 ! 1 !}\)
= \(\frac{7 \times 6}{2 \times 1} \times 4\)
= 84
(b) 4 girls and 1 boy

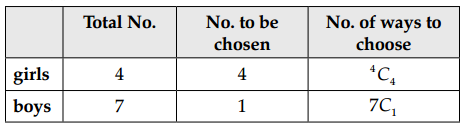
Number of ways selecting = ⁷C₁ × ⁴C₄
= \(\frac{7 !}{1 ! 6 !} \times \frac{4 !}{4 ! 0 !}\)
= 7 × 1
= 7
∴ Total number of ways = 84 + 7 = 91
(iii) at least one girl and one boy?
A group giving at least one boy and one girl will consist of
(a) 1 boy and 4 girls
(b) 2 boys and 3 girls
(c) 3 boys and 2 girls
(d) 4 boys and 1 girl
Number of ways of selecting 1 boy and 4 girls = ⁷C₁ × ⁴C₄ = 7
Number of ways of selecting 2 boys and 3 girls = ⁷C₂ × ⁴C₃ = 84
Number of ways of selecting 3 boys and 2 girls = ⁷C₃ × ⁴C₂ = 210
Number of ways of selecting 4 boys and 1 girl = ⁷C₄ × ⁴C₁ = 140
Hence, total number of ways = 7 + 84 + 210 + 140 = 441 ways.

Section-D

[This section comprises long answer type questions (LA) of 5 marks each]

Question 32.
A manufacturer has 900 litres of a 15% solution of acid. How many litres of a 40% add solution must be added to it so that add content in the resulting mixture will be more than 20% but less than 25%?
Answer:
Let x litres of 40% acid solution is required to be added.
Then, Total mixture = (x + 900) litres
Therefore, 40% of x + 15% of 900 > 20% of (x + 900) and 40% of x + 15% of 900 < 25% of (x + 900)
⇒ \(\frac{40}{100}\)x + \(\frac{15}{100}\) × 900 > \(\frac{20}{100}\) × (x + 900)
and \(\frac{40}{100}\)x + \(\frac{15}{100}\) × 900 > \(\frac{25}{100}\) × (x + 900)
⇒ 40x + 13500 > 20x + 18000 and 40x + 13500 < 25x + 22500
⇒ 20x > 4500 and 15x < 9000
⇒ x > 225 and x < 600
⇒ 225 < x < 600
Thus, the number of litres of the 40% solution of acid will have to be more than 225 litres but less than 600 litres.

Question 33.
Solve: \(\frac{|x|-1}{|x|-2}\) ≥ 0, x ∈ R, x ≠ ±2
O
If |z + 1| = z + 2(1 + i) then find z.
Answer:
We have, \(\frac{|x|-1}{|x|-2}\) ≥ 0
⇒ \(\frac{y-1}{y-2}\) ≥ 0, where y = |x|
⇒ y ≤ 1 or y > 2

⇒ |x| ≤ 1 or |x| > 2
⇒ (-1 ≤ x ≤ 1) or (x < -2 or x > 2)
⇒ x ∈ [-1, 1] or x ∈ (-∞, -2) ∪ (2, ∞)
⇒ x ∈ [-1, 1] ∪ (-∞, -2) ∪ (2, ∞)
Hence, solution set of the given inequation is [-1, 1] ∪ (-∞, -2) ∪ (2, ∞).
OR
Given that: |z + 1| = z + 2(1 + i)
Let z = x + iy
So, |x + iy +1| = (x + iy) + 2(1 + i)
⇒ |x + 1 + iy| = x + iy + 2 + 2i
⇒ |(x + 1) + iy| = (x + 2) + i(y + 2)
⇒ √[(x + 1)² + y²] = (x + 2) + i(y + 2)
Squaring both sides, we get
⇒ (x + 1)² + y² = (x + 2)² + (y + 2)² . i² + 2(x + 2)(y + 2)i
⇒ x² + 1 + 2x + y² = x² + 4 + 4x + [y² + 4 + 4y] (-1) + 2i(xy + 2x + 2y + 4)
⇒ x² + y² + 2x + 1 = x² + 4x + 4 – y² – 4y – 4 + i(2xy + 4x + 4y + 8)
⇒ 2y² – 2x + 4y + 1 – i[2x(y + 2) + 4(y + 2)] = 0
⇒ 2y² – 2x + 4y + 1 – i[(2x + 4)(y + 2)] = 0
⇒ 2y² – 2x + 4y + 1 – 2i[(x + 2)(y + 2)] = 0
Comparing the real and imaginary parts, we get
2y2 – 2x + 4y + 1 = 0 …..(i)
and (x + 2)(y + 2) = 0
⇒ x + 2 = 0 or y + 2 = 0
∴ x = -2 or y = -2
Now put x = -2 in equation (i)
2y² – 2(-2) + 4y + 1 = 0
⇒ 2y²2 + 4 + 4y + 1 = 0
⇒ 2y² + 4y + 5 = 0
b² – 4ac = (4)² – 4 × 2 × 5
= 16 – 40
= -24 < 0, no real roots.
Put y = -2 in eqn. (i)
2(-2)² – 2x + 4(-2) + 1 = 0
⇒ 8 – 2x – 8 + 1 = 0
⇒ x = \(\frac{1}{2}\) and y = -2
Hence, z = x + iy = (\(\frac{1}{2}\) – 2i)

Question 34.
Find the mean, variance and standard deviation using short cut method.

Answer:


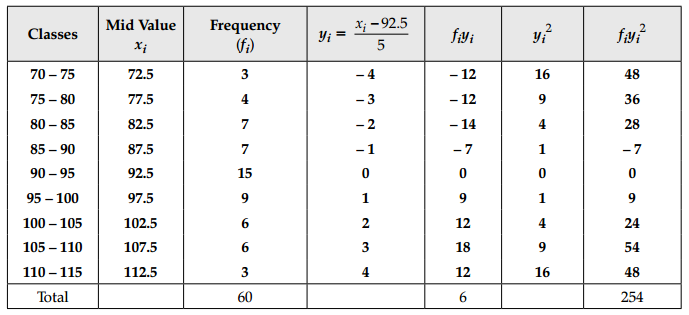
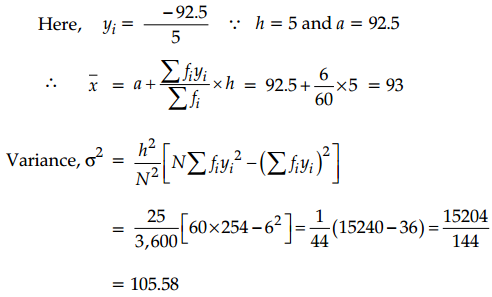
∴ Mean = 93, Variance = 105.58
and Standard deviation = √105.58 = 10.27

Question 35.
Find the co-ordinates of the circumcentre of the triangle whose vertices are (4, 3), (-2, 3) and (6, -1).
OR
Find the equation of the set of points P, the sum of whose distances from A(4, 0, 0) and B(-4, 0, 0) is equal to 10.
Answer:
The given vertices are A(4, 3), B(-2, 3) and C(6, -1).

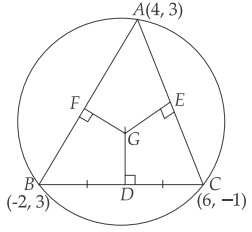
Let G be the circumcentre of ΔABC (i.e., the point of concurrence of right bisectors GD, GE and GF) and (h, k) be the coordinate of G.
∴ D = mid-point of BC = \(\left(\frac{-2+6}{2}, \frac{3-1}{2}\right)\) = (2, 1)
E = mid-point of AC = \(\left(\frac{4+6}{2}, \frac{3-1}{2}\right)\) = (5, 1)
F = mid-point of AB = \(\left(\frac{4-2}{2}, \frac{3+3}{2}\right)\) = (1, 3)
Given, GD ⊥ BC
∴ Slope of GD × slope of BC = -1
⇒ \(\frac{1-k}{2-h} \times \frac{-1-3}{6+2}\) = -1
⇒ \(\frac{1-k}{2-h} \times\left(-\frac{1}{2}\right)\) = -1
⇒ 1 – k = 4 – 2h
⇒ 2h – k = 3 ……(i)
and, Slope of GE × slope of AC = -1
⇒ \(\frac{1-k}{5-h} \times \frac{-1-3}{6-4}\) = -1
⇒ \(\frac{1-k}{5-h}\) (-2) = -1
⇒ 2 – 2k = 5 – h
⇒ h – 2k = 3 …….(ii)
From (i) and (ii),
h = 1, k = -1
∴ The coordinates of the circumcentre are (1, -1).
OR
Let P(x, y, z) be the point
∴ PA + PB = 0
⇒ \(\sqrt{(x-4)^2+(y-0)^2+(z-0)^2}\) + \(\sqrt{(x+4)^2+(y-0)^2+(z-0)^2}\) = 10
⇒ \(\sqrt{(x-4)^2+y^2+z^2}+\sqrt{(x+4)^2+y^2+z^2}\) = 10
⇒ \(\sqrt{(x-4)^2+y^2+z^2}=10-\sqrt{(x+4)^2+y^2+z^2}\)
⇒ (x – 4)² + y² + z² = 100 – 20\(\sqrt{(x+4)^2+y^2+z^2}\) + (x + 4)² + y² + z²
⇒ (x -4)² – (x + 4)² – 100 = -20\(\sqrt{(x+4)^2+y^2+z^2}\)
⇒ x² – 8x + 16 – x² – 8x – 16 – 100 = -20\(\sqrt{(x+4)^2+y^2+z^2}\)
⇒ -16x – 100 = -20\(\sqrt{(x+4)^2+y^2+z^2}\)
⇒ (4x + 25) = 5\(\sqrt{(x+4)^2+y^2+z^2}\)
⇒ (4x + 25)² = 25(x + 4)² + 25y² + 25z²
⇒ 16x² + 200x + 625 = 25x² + 200x + 400 + 25y² + 25z²
⇒ 9x² + 25y² + 25z² = 225

Section-E

[This section comprises of 3 case- study/passage-based questions of 4 marks each with subparts.]

The first two case study questions have three subparts (i), (ii), (iii) of marks 1,1,2 respectively. The third case study question has two subparts of 2 marks each.

Question 36.
Read the following passage and answer the questions given below:
During the Mathematics class, a teacher clears the concept of permutation and combination to the 11th standard students. After the class he asks the students some questions as follows.
(i) In how many ways numbers between 99 and 1000 (both excluding) can be formed such that every digit is either 3 or 7?
(ii) In how many ways numbers between 99 and 1000 (both excluding) can be formed such that there is no restriction?
(iii) In how many ways numbers between 99 and 1000 (both excluding) can be formed such that no digit is repeated?
OR
In how many ways numbers between 99 and 1000 (both excluding) can be formed such that the digit at hundred’s place is 7?
Answer:
(i) Numbers between 99 and 1000 both exclude means from 100 to 999, i.e., 3-digit numbers.
Fix the three positions with 3 or 7, then the number of ways that every digit is either 3 or 7 is = 2 × 2 × 2 = 8 ways
(ii) Now, there is no restriction that means we can use any number to form 3-digit numbers, we cannot put 0 at hundredth place otherwise the number will become 2-digit, so the number of ways of forming 3-digit numbers is 9 × 10 × 10 = 900 ways
(iii) Now, no digit is repeated, meaning we can use a single digit only one time, so the number of ways is 9 × 9 × 8 = 648 ways
OR
Now, the digit at hundreds of places is 7, fix 7 at the hundredth place, number of ways is 1 × 10 × 10 = 100 ways.

Question 37.
Read the following passage and answer the questions given below:
The logarithmic function expressed as log_e R+ → R and given by log_e x = y iff e^y = x. The graph of the function is given below:

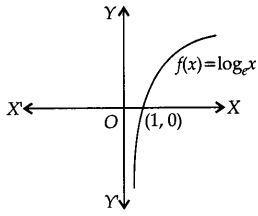
(a) Domain of f(x) = (0, ∞) or R+
(b) Range of f(x) = (-∞, ∞) or R
To find the limit of functions involving logarithmic function, we use the following theorem:
\(\lim _{x \rightarrow 0} \frac{\log _e(1+x)}{x}=1\)
(i) Evaluate: \(\lim _{x \rightarrow 0} \frac{\log _e(1+5 x)}{x}\)
(ii) Evaluate: \(\lim _{x \rightarrow 0} \frac{\log _e(1+6 x)-5 x^2}{x}\)
(iii) Evaluate: \(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-1}{\log (1+x)}\)
OR
Evaluate: \(\lim _{x \rightarrow 5} \frac{\log x-\log 5}{x-5}\)
Answer:

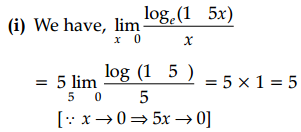
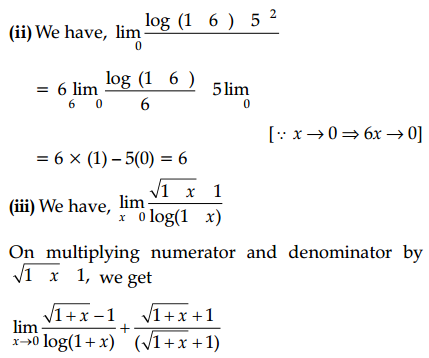
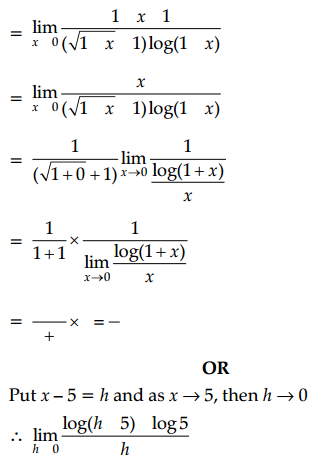
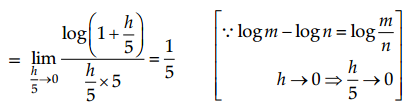
Question 38.
Read the following passage and answer the questions given below:
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently, the sample space consists of four elementary outcomes S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John’s promotion is same as that of Gurpreet, Rita’s chances of promotion are twice as likely as Johns. Aslam’s chances are four times that of John.
(i) What is the probability that John got promotion?
(ii) What is the probability that Rita got promotion?
Answer:
Let Event:
J = John promoted
R = Rita promoted
A = Aslam promoted
G = Gurpreet promoted
Given sample space, S = (John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}
i.e., S = (J, R, A, G)
It is given that, chances of John’s promotion is same as that of Gurpreet.
P(J) = P(G)
Rita’s chances of promotion are twice as likely as John.
P(R) = 2P(J)
and Aslam’s chances of promotion are four times that of John.
P(A) = 4P(J)
(i) Now, P(J) + P(R) + P(A) + P(G) = 1
⇒ P(J) + 2P(J) + 4P(J) + P(J) = 1
⇒ 8P(J) = 1
⇒ P(J) = P(John Promoted) = \(\frac{1}{8}\)
(ii) P(Rita promoted) = P(R)
= 2P(J)
= 2 × \(\frac{1}{8}\)
= \(\frac{1}{4}\)