CBSE Sample Papers for Class 11 Applied Mathematics Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Set 3 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

• This Question paper contains five sections A, B, C, D and E. Each section is compulsory. However, there is some internal choice in some questions.
• Section A has 18 MCQs and 2 Assertion Reason-based questions of 1 mark each.
• Section B has 5 Very Short Answer (VSA) questions of 2 marks each.
• Section C has 6 Short Answer (SA) questions of 3 marks each.
• Section D has 4 Long Answer (LA) questions of 5 marks each.
• Section E has 3 source-based/case-based/passage-based/integrated units of assessment (4 marks each) with subparts.
• Internal Choice is provided in 2 questions in Section B, 2 questions in Section C, 2 Questions in Section D. You have to attempt only one alternative in all such questions.

Section-A

(All Questions are compulsory. No internal choice is provided in this section)

Question 1.
If the decimal number is a fraction then its binary equivalent is obtained by __________ the number continuously by 2.
(a) adding
(b) subtracting
(c) multiplying
(d) dividing
Answer:
(c) multiplying
Explanation:
On multiplying the decimal continuously by 2, the binary equivalent is obtained by the collection of the integer part. However, if if s binary equivalent is determined by dividing the number by 2 and collecting the remainders.

Question 2.
The average of four consecutive even numbers is 27, then the largest number is
(a) 24
(b) 30
(c) 32
(d) None of these
Answer:
(b) 30
Explanation:
Let the numbers be x, x + 2, x + 4, and x + 6. Then,
\(\frac{x+(x+2)+(x+4)+(x+6)}{4}\) = 27 [given]
⇒ \(\frac{4 x+12}{4}\) = 27
⇒ x + 3 = 27
⇒ x = 24
∴ Largest number = (x + 6) = 24 + 6 = 30

Question 3.
The hands of the clock are straight, __________ times in a day.
(a) 12
(b) 22
(c) 24
(d) 44
Answer:
(d) 44
Explanation:
In 12 hours, the hands coincide or are in opposite direction 22 times.
∴ In 24 hours, the hands coincide or are in opposite direction 44 times a day.

Question 4.
‘A’ can finish a work in 18 days ’B’ can do the same work in half the time taken by ‘A’ then, working together, __________ part of the same work they can finish in a day.
(a) 1/6th part
(b) 1/5th part
(c) 1/4th part
(d) 1/2th part
Answer:
(a) 1/6th part
Explanation:
A’s 1 day’s work = \(\frac{1}{18}\)
B’s 1 day’s work = \(\frac{1}{9}\)
∴ (A + B)’s 1 day’s work = \(\left(\frac{1}{18}+\frac{1}{9}\right)=\frac{1}{6}\)
Hence, A and B together finish \(\frac{1}{6}\) part of the work in a day.

Question 5.
If A = set of letters of the word ‘DELHI’ and B = the set of letters of the word ‘DOLL’, then A ∪ B is
(a) {D, H, I, L, O}
(b) {D, E, H, I, L}
(c) {D, E, H, I, L, O}
(d) {D, E, H, I, L, L}
Answer:
(c) {D, E, H, I, L, O}
Explanation:
Here, A = {D, E, H, I, L} and B = {D, L, O}
A ∪ B = {D, E, H, I, L} ∪ {D, L, O} = {D, E, H, I, L, O}

Question 6.
Let n(A) = m, and n(B) = n. Then the total number of possible relations that can be defined from A to B is
(a) mⁿ
(b) n^m – 1
(c) mn – 1
(d) 2^mn
Answer:
(d) 2^mn
Explanation:
Given, n(A) = m and n(B) = n
∴ n(A × B) = n(A) . n(B) = mn
So, the total number of non-empty relations from A to B = 2^mn

Question 7.
The number of terms in the A.P. 7,10,13,……., 31 is
(a) 7
(b) 9
(c) 11
(d) 15
Answer:
(b) 9
Explanation: Given, AP is 7, 10, 13,……., 31
Here, a = 7, l = 31 and d = 3
Using formula, l = a + (n – 1)d
⇒ 31 = 7 + (n – 1)3
⇒ 31 – 7 = 3n – 3
⇒ 24 + 3 = 3n
⇒ n = 9

Question 8.
Find the odd one out.
(a) 121
(b) 253
(c) 286
(d) 372
Answer:
(d) 372
Explanation:
The sum of the first and last digit equals to the middle digit.
i.e., (a) 1 + 1 = 2, (b) 2 + 3 = 5, (c) 2 + 6 = 8 but (d) 3 + 2 ≠ 7

Question 9.
If f(x) = x³, then the value of \(\frac{f(5)-f(1)}{5-1}\) is
(a) 125
(b) 101
(c) 71
(d) 31
Answer:
(d) 31
Explanation:
Given, f(x) = x³
At x = 5, f(5) = 5³ = 125
At x = 1, f(1) = 1³ = 1
∴ \(\frac{f(5)-f(1)}{5-1}\) = \(\frac{125-1}{5-1}\)
= \(\frac{124}{4}\)
= 31

Question 10.
The domain and range of the function f given by f(x) = 2 – |x – 5| is
(a) Domain = R+, Range = (-∞, 1]
(b) Domain = R, Range = (-∞, 2]
(c) Domain = R, Range = (-∞, 2)
(d) Domain = R+, Range = (-∞, 2]
Answer:
(b) Domain = R, Range = (-∞, 2]
Explanation:
We have, f(x) = 2 – |x – 5|
Clearly, f(x) is defined for all x ∈ R
∴ The Domain of f = R
Now, |x – 5| ≥ 0, ∀ x ∈ R
⇒ -|x – 5| ≤ 0
⇒ 2 – |x – 5| ≤ 2
∴ f(x) ≤ 2
∴ Range of f = (-∞, 2].

Question 11.
The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then the probability of neither A nor B is
(a) 0.2
(b) 0.4
(c) 0.7
(d) None of these
Answer:
(a) 0.2
Explanation:
Given, P(A) = 0.5, P(B) = 0.3 and P(A ∩ B) = 0
[∵ A and B are mutually exclusive events]
Now, Probability that neither A nor B = \(P(\bar{A} \cap \bar{B})\)
= \(P(\overline{A \cup B})\)
= 1 – [P(A ∪ B)]
= 1 – [P(A) + P(B) – P (A ∩ B)]
= 1 – [0.5 + 0.3 – 0]
= 1 – 0.8
= 0.2

Question 12.
Mean deviation of n observations x₁, x₂,……..,x_n from their mean \(\bar{x}\) is
(a) \(\sum_{i=1}^n\left(x_i-\bar{x}\right)\)
(b) \(\frac{1}{n} \sum_{i=1}^n\left|x_i-\bar{x}\right|\)
(c) \(\sum_{i=1}^n\left(x_i-\bar{x}\right)^2\)
(d) \(\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2\)
Answer:
(b) \(\frac{1}{n} \sum_{i=1}^n\left|x_i-\bar{x}\right|\)
Explanation:
Mean Deviation, M.D. = \(\frac{1}{n} \sum_{i=1}^n\left|x_i-\bar{x}\right|\)
where, \(\bar{x}\) is mean and n is number of observations

Question 13.
The standard deviations for first ten natural numbers is
(a) 5.5
(b) 3.87
(c) 2.97
(d) 2.87
Answer:
(d) 2.87
Explanation:
We know that
S.D. of first n natural numbers = \(\sqrt{\frac{n^2-1}{12}}\)
Here, n = 10
∴ S.D. = \(\sqrt{\frac{(10)^2-1}{12}}\)
= \(\sqrt{\frac{99}{12}}\)
= \(\sqrt{8.25}\)
= 2.87

Question 14.
The acute angle between the lines x + y = 0 and y = 0 is
(a) 45°
(b) 60°
(c) 90°
(d) 0°
Answer:
(a) 45°
Explanation:
The given lines are x + y = 0 and y = 0
Here, A₁ = 1, B₁ = 1, A₂ = 0, B₂ = 1
Angle ‘θ’ between the lines is given by
θ = \(\tan ^{-1}\left|\frac{A_1 B_2-A_2 B_1}{A_1 A_2+B_1 B_2}\right|\)
= \(\tan ^{-1}\left|\frac{1-0}{0+1}\right|\)
= tan^-1(1)
= 45°

Question 15.
The vertex of parabola (y + a)² = 8a(x – a) is
(a) (-a, -a)
(b) (a, -a)
(c) (-a, a)
(d) None of these
Answer:
(b) (a, -a)
Explanation:
The given equation of parabola is (y + a)² = 8a(x – a)
Put X = x – a and Y = y + a
i.e., Y² = 8aX
Vertex = (X = 0, Y = 0)
= (x – a = 0, y + a = 0)
= (x = a, y = -a)
Hence, the vertex is at (a, -a)

Question 16.
The least number of complete years in which a sum of money put out at 20% compound interest will be more than doubled is:
(a) 2 years
(b) 4 years
(c) 5 years
(d) 6 years
Answer:
(b) 4 years
Explanation:
According to the question,
\(P\left(1+\frac{20}{100}\right)^n\) > 2P
\(\left(\frac{6}{5}\right)^n\) > 2
Now, \(\left(\frac{6}{5} \times \frac{6}{5} \times \frac{6}{5} \times \frac{6}{5}\right)\) > 2
So, n = 4 years

Question 17.
GST is a consumption of goods and service tax based on
(a) Development
(b) Dividend
(c) Destiny
(d) Destination
Answer:
(d) Destination

Question 18.
kl is a unit of
(a) liquid
(b) solid
(c) gas
(d) None of these
Answer:
(a) liquid
Explanation:
kl = kilolitre, it is the unit of liquid.

Direction (Q.19 & Q.20): In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.

(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.

Question 19.
Assertion (A): The length of the longest pole that can be placed in a room 12 m long 8 m broad and 9 m high is 17 m.
Reason (R): Length of longest pole is equal to the length of the diagonal of the room.
Answer:
(a) Both (A) and (R) are true and (R) is the correct explanation of (A).
Explanation:
Length of longest pole = length of the diagonal of the room = \(\sqrt{l^2+b^2+h^2}\)
Here, l = 12 m, b = 8 m, h = 9 m
∴ Length of longest pole = \(\sqrt{(12)^2+(8)^2+(9)^2}\)
= \(\sqrt{289}\)
= 17

Question 20.
Assertion (A): Present value of an annuity regular is C.F. × \(\frac{\left[(1+i)^n-1\right]}{i(1+i)^n}\)
Reason (R): Future value of an annuity regular is C.F. × \(\left[\frac{(1+i)^n-1}{i}\right]\)
Answer:
(b) Both (A) and (R) are true but (R) is not the correct explanation of (A).

Section-B

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 21.
‘Ram’ is the father of ‘Kusha’ but ‘Kusha’ is not his son. ‘Mala’ is the daughter of ‘Kusha’. ‘Shalaka’ is the spouse of ‘Ram’. ‘Gopal’ is the brother of ‘Kusha’. ‘Hari’ is the son of ‘Gopal’. ‘Meena’ is the spouse of ‘Gopal’. ‘Ganpat’ is the father of ‘Meena’. Who is the grand daughter of ‘Ram’?
Answer:

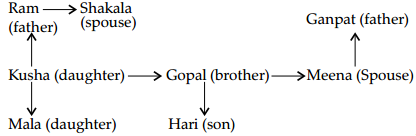
Here, we can see ‘Mala’ is the daughter of ‘Kusha’ and ‘Ram is the father of ‘Kusha’. So, ‘Mala’ is the grand-daughter of ‘Ram.

Question 22.
What is the probability that a given two-digit number is divisible by 15?
OR
A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that one ball is red and two balls are white.
Answer:
No. of two digits numbers = 90
⇒ n(S) = 90
Let ‘A’ be the event of getting a number divisible by 15.
A = {15, 30, 45, 60, 75, 90}
⇒ n(A) = 6
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{90}=\frac{1}{15}\)
∴ The probability of getting a number divisible by 15 = \(\frac{1}{15}\).
OR
∵ Number of red balls = 8
and number of white balls = 5
P(one ball is red and two balls are white) = \(\frac{{ }^8 C_1 \times{ }^5 C_2}{{ }^{13} C_3}\)
= \(\frac{8 \times 10}{\frac{13 \times 12 \times 11}{3 \times 2 \times 1}}\)
= \(\frac{40}{143}\)

Question 23.
Show that for any numbers a and b S.D. is given by \(\frac{|a-b|}{2}\).
OR
For some symmetrical distribution, Q₁ = 36 and Q₃ = 63. Using Bowely’s measures of skewness, find the median.
Answer:
For two numbers a and b, given by
\(\bar{x}=\frac{(a+b)}{2}\)

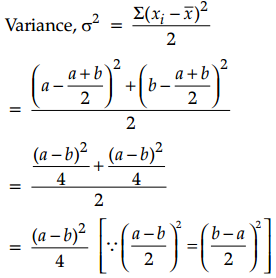
∴ Standard Deviation = \(\frac{|a-b|}{2}\)
(The absolute sign is taken, as S.D. cannot be negative)
OR
For symmetrical distribution, skewness = 0
Given, Q₁ = 36 and Q₃ = 63
Since, S_k = \(\frac{Q_3+Q_1-2 Q_2}{Q_3-Q_1}\)
⇒ 0 = \(\frac{63+36-2 Q_2}{63-36}\)
⇒ 2Q₂ = 99
⇒ Q₂ = 49.5
∴ Q₂ = median = 49.5

Question 24.
For an industrial connection monthly consumption of electricity units are 250, calculate the electricity bill. Tariff rates can be considered the table given below:

Unit Slab	Rate Per Unit (in ₹)	Fixed Charge
1-300	7.50	330
301-500	8.40	390
501 and above	8.75	450

Electricity duty is considered as 5%.
Answer:

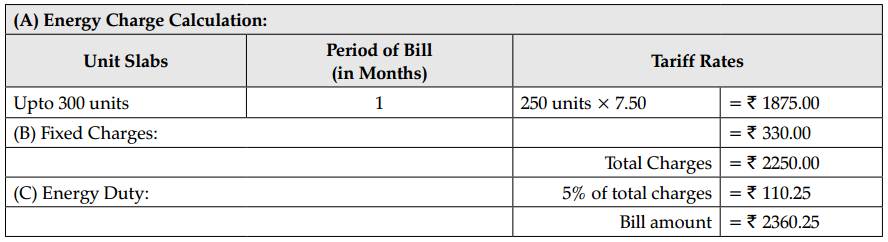
Thus, final bill amount is ₹ 2360.25.

Question 25.
(a) A dealer in Agra (U.P.), say Ramesh, supplies products and services worth ₹ 10,000 to Suresh a person in Lucknow (U.P.). If the rate of GST is 28% find the SGST.
(b) A dealer in Bhopal (M.P.). supplies products and services worth ₹ 5,000 to another dealer in Kanpur (UP). If the rate of GST is 28%, find the tax levied under CGST.
Answer:
(a) Since, the GST rate is 28%,
∴ SGST rate is 14%.
i.e, SGST = 14% of ₹ 5,000
= ₹ \(\frac{14}{100}\) × 5,000
= ₹ 700

(b) Since, the given case is of inter-state transaction as the products/services is supplied from one state to another.
∴ CGST = 0

Section-C

(All Questions are compulsory. In case of internal Choice, attempt any one question only)

Question 26.
A carpenter was hired to build 192 window frames. The first day he made five frames and each day, thereafter he made two more frames than he made the day before. How many days did it take him to finish the job?
OR
Let A = {1, 2, 3, 4}, B = {1, 4, 9, 16, 25} and R be a relation defined from A to B as, R = {(x, y) : x ∈ A, y ∈ B and y = x²}
(i) Depict this relation using arrow diagram.
(ii) Find domain of R.
(iii) Find range of R.
(iv) Write co-domain of R.
Answer:
Here, a = 5 and d = 2
Let he finished the job in n days.
Then, S_n = 192
⇒ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
⇒ 192 = \(\frac{n}{2}\)[2 × 5 + (n – 1)2]
⇒ 192 = \(\frac{n}{2}\)[10 + 2n – 2]
⇒ 192 = \(\frac{n}{2}\)[8 + 2n]
⇒ 192 = 4n + n²
⇒ n² + 4n – 192 = 0
⇒ (n – 12)(n + 16) = 0
⇒ n = 12, -16
⇒ n = 12 [∵ n ≠ -16]
OR
Given, A = {1, 2, 3, 4} and B = {1, 4, 9, 16, 25} and R = {(x, y) : x ∈ A, y ∈ B and y = x²}
(i) Relation R = {(1, 1), (2, 4), (3, 9), (4, 16)}

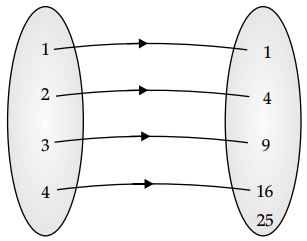
(ii) Domain of R = {1, 2, 3, 4}
(iii) Range of R = {1, 4, 9, 16}
(iv) Co-domain of R = {1, 4, 9, 16, 25}

Question 27.
In the following table some capital alphabets are written in a row, below them their coding have been given. Now in questions a particular word has been coded in a particular manner using codes as given below the capital letter. You have to understand the pattern of coding and answer the following questions.

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

u

a

2

v

b

w

3

t

4

x

s

y

5

z

6

c

d

8

7

e

r

h

9

i

p

q

(i) If DASH is coded as 2 a 8 4, then what is the code for SMASH?
(ii) If FASHION is coded as aatAcx, then what is the code for POSITION?
(iii) If DEER is coded as vw8 and TOSS is coded as e6e, then what is the code for DOTT?
Answer:
(i) In the word DASH, letters at the odd places have been moved one place back and letters at the even places have been moved one place ahead regarding the position of codes given in the table. Therefore, SMASH can be coded as 8zqe3.

(ii) The codes for the respective letters of the FASHION as per table have been reversed in the coding. So, POSITION can be coded as z64e476c.

(iii) In both the words DEER and TOSS, codes for each letters have been used just below the letters in the table except for the letter that has been written twice i.e., E and S. For these letters, codes have been used just one position ahead in the table that too only one. Therefore, DOTT can be codded as v6r.

Question 28.
If (x² + y²)² = xy, find \(\frac{d y}{d x}\).
Answer:
Given, (x² + y²)² = xy
Differentiating with respect to x

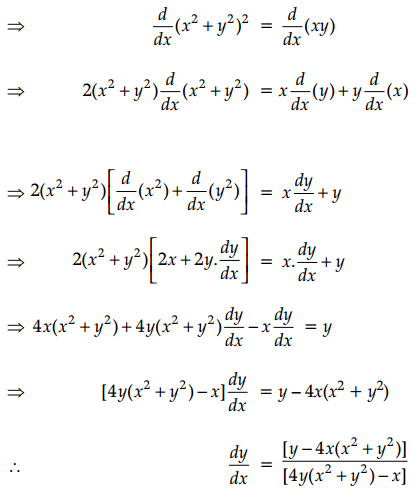
Question 29.
Compute the correlation coefficient between x and y from the following data:
N = 10, Σxy = 220, Σx² = 200, Σy² = 262, Σx = 40 and Σy = 50.
Answer:
We know that

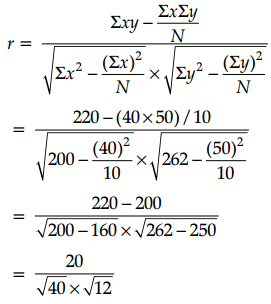
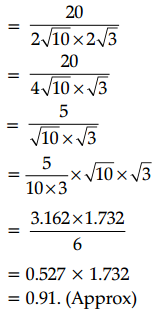
Question 30.
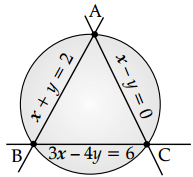
Find the equation of the circle passing through the vertices of a triangle whose sides are represented by the equations x + y = 2, 3x – 4y = 6 and x – y = 0.
OR
If two diameters of a circle lie along the lines x – y – 9 = 0 and x – 2y – 7 = 0 and the area of the circle is 38.5 sq. units, find the equation.
Answer:
Let AB, BC and CA represent the three sides of the triangle given by x + y = 2, 3x – 4y = 6 and x – y = 0, respectively.
On solving AB and BC, we get the coordinates of vertex B(2, 0)
On solving BC and CA, we get the coordinates of vertex C(- 6, – 6)
On solving AB and CA, we get the coordinates of vertex A(1, 1)
Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0 …….(i)

Since, the circle (i) passes through A(1, 1), B(2, 0) and C(-6, -6), so, equation (i) implies
1² + 1² + 2g.1 + 2f.1 + c = 0
⇒ 2g + 2f + c = -2 ……(ii)
2² + 0² + 2g.2 + 2f.0 + c = 0
⇒ 4g + c + 4 = 0 ……..(iii)
and (-6)² + (-6)² + 2g.(-6) + 2f.(-6) + c = 0
⇒ 12g + 12f – c = 72 ……(iv)
Solving equations (ii), (iii), (iv), we get
g = 2, f = 3, c = -12
Now, putting the value of g, f, c in equation (i)
x² + y² + 4x + 6y – 12 = 0 is the required equation of the circle.
OR
Given, two diameters of a circle lie along the lines
x – y – 9 = 0 …….(i)
and x – 2y – 7 = 0 ……(ii)
So, their point of intersection is the centre of the circle.
Solving equations (i) and (ii), simultaneously, we get
x = 11 and y = 2
∴ The centre of the circle is (11, 2)
Let r be the radius of the circle, then
area = πr² = 38.5 sq units [given]
⇒ \(\frac{22}{7} r^2=\frac{77}{2}\)
⇒ r² = \(\frac{49}{4}\)
⇒ r = \(\frac{7}{2}\)
∴ The equation of the circle is (x – 11)² + (y – 2)² = \(\left(\frac{7}{2}\right)^2\)
⇒ x² + y² – 22x – 4y + 125 = \(\frac{49}{4}\)
⇒ x² + y² – 22x – 4y + 125 – \(\frac{49}{4}\) = 0
⇒ 4(x² + y²) – 88x – 16y + 451 = 0

Question 31.
Anil bought a TV costing ₹ 13000 by making a down payment of ₹ 3000 and agreeing to make equal annual payment for three years. How much would be each payment if the interest on unpaid amount be 14% compounded annually?
Answer:
In the present case, we have present value of annuity (13000 – 3000) = ₹ 10000
and we have to calculate equal annual payment over the period of 3 years.
We know that,


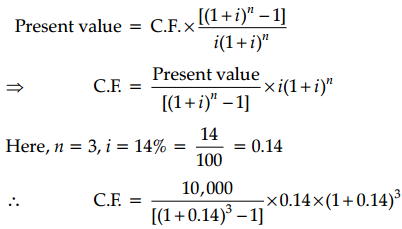
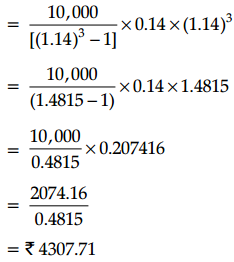
Therefore each payment would be ₹ 4307.71.

Section-D

(This section comprises long answer type questions (LA) of 5 marks each)

Question 32.
Sum of the first p, q and r terms of an A.P. are a, b and c respectively. Prove that \(\frac{a}{p}(q-r)+\frac{b}{q}(r-p)+\frac{c}{r}(p-q)=0\)
OR
In how many ways can be letters of the word PERMUTATIONS be arranged if the
(i) Words start with P and end with S,
(ii) Vowels are all together,
(iii) There are always 4 letters between P and S?
Answer:
Let the first term is A and common difference is d.
Given, S_p = \(\frac{p}{2}\)[2A + (p – 1)d] = a …(i)
(∵ S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S_q = \(\frac{q}{2}\)[2A + (q – 1)d] = b ……(ii)
and S_r = \(\frac{r}{2}\)[2A + (r – 1)d] = c …..(iii)
Now, we are to prove \(\frac{a}{p}(q-r)+\frac{b}{q}(r-p)+\frac{c}{r}(p-q)=0\)
L.H.S. = \(\frac{a}{p}(q-r)+\frac{b}{q}(r-p)+\frac{c}{r}(p-q)\)
Putting the values of a, b and c from Equations (i), (ii) and (iii) respectively, we get
L.H.S. = \(\frac{1}{p} \times \frac{p}{2}\)[2A + (p – 1)d](q – r) + \(\frac{1}{q} \times \frac{q}{2}\)[2A + (q – 1)d](r – p) + \(\frac{1}{r} \times \frac{r}{2}\) [2A + (r – 1)d](p – q)
= \(\frac{1}{2}\)[{{2A + (p – 1)d}(q – r) + {2A + (q – 1)d}(r – p) + [2A + (r – 1)d}(p – q)]]
= \(\frac{1}{2}\)[2A(q – r) + (p – 1) d(q – r) + 2A(r – p) + (q – 1)d(r – p) + 2A(p – q) + (r – 1) d(p – q)]
= \(\frac{1}{2}\)[2A(q – r + r – p + p – q) + d[(p – 1)(q – r) + (q – 1)(r – p) + (r – 1)(p – q)]]
= \(\frac{1}{2}\)[2A × (0) + d(pq – pr – q + r + qr – pq – r + p + rp – rq – p + q)]
= \(\frac{1}{2}\)(0 + d × 0)
= 0
∴ L.H.S. = R.H.S.
Hence proved.
OR
(I) Letters between P and S are ERMUTATION.
These 10 letters having T two times.
These letters can be arranged in \(\frac{10 !}{2 !}\) = 1814400 ways.

(ii) There are 12 letters in the word PERMUTATIONS which have T two times.
Now, the vowels A, E, I, O, U are taken together.
Let it be considered in one block.
The letters of vowels can be arranged in 5! ways.
Thus, there are 7 letters and 1 block of vowels with T two times.
∴ Required number of arrangements = \(\frac{8!}{2!}\) × 5! = 24, 19, 200

(iii) There are 12 letters to be arranged in 12 places

These 12 letters are to be filled in 12 places shown above.
P may be filled up at place No. 1, 2, 3, 4, 5, 6, 7 and consequently S may be filled up at place No. 6, 7, 8, 9, 10, 11, 12 leaving four places in between.
Now P and S may be filled up in 7 ways.
Similarly, S and P may be filled in 7 ways.
Remaining ten letters having two T’s
∴ These can be arranged in \(\frac{10!}{2!}\) ways
Hence, the total number of required permutations = 2 × 7 × \(\frac{10!}{2!}\) ways
= 14 × 1814400 ways
= 25401600 ways

Question 33.
Find the value of ‘a’ and ‘b’ if \(\lim _{x \rightarrow 2} f(x)\) and \(\lim _{x \rightarrow 4} f(x)\) exists where f(x) = \(\left\{\begin{array}{cc}
x^2+a x+b, & 0 \leq x<2 \\
3 x+2, & 2 \leq x \leq 4 \\
2 a x+5 b, & 4 \end{array}\right.\)
Answer:

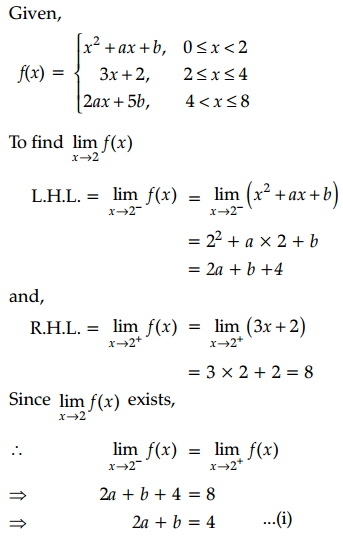
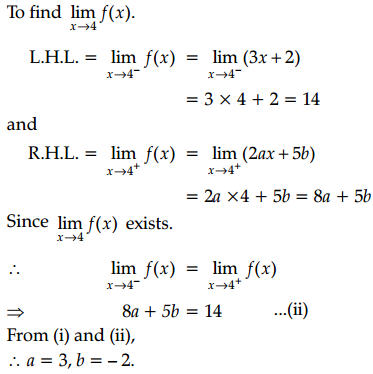
Question 34.
Calculate, the P.R. for the scores 35 and 55 for the distribution of scores give in the following table:

Scores	10-19	20-29	30-39	40-49	50-59	60-69	70-79	80-89	90-99
f	2	4	5	10	35	20	13	8	3

OR
From the data given below state which group is more variable, A or B?

Marks	10-20	20-30	30-40	40-50	50-60	60-70	70-80
Group A	9	17	32	33	40	10	9
Group B	10	20	30	25	43	15	7

Answer:

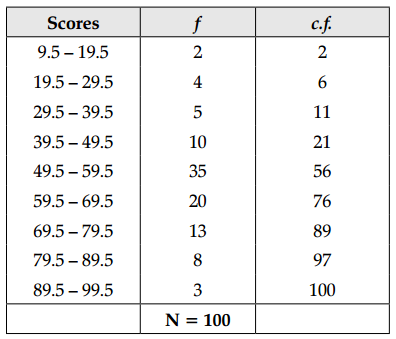
We use formula, P.R. = \(\frac{100}{N}+\left(\text { c.f. }+\frac{X-l}{i} \times f\right)\)
(i) For x = 35,
X lies between the class 29.5 – 39.5
So, c.f. = 6, l = 29.5, f = 5, i = 10, N = 100
∴ P.R. = \(\frac{100}{100}+\left(6+\frac{35-29.5}{10} \times 5\right)\)
= 1 + (6 + \(\frac{5.5}{2}\))
= 1 + (6 + 2.75)
= 9.75
Thus, percentile ranking of 35 is 9.75.

(ii) For X = 55,
X lies between the class 49.5 – 59.5
So, c.f. = 21, l = 49.5, f = 35, i = 10, N = 100
∴ P.R. = \(\frac{100}{100}+\left(21+\frac{(55-49.5)}{10} \times 35\right)\)
= 1 + (21 + 19.25)
= 41.25
Thus, percentile ranking of 55 is 41.25.
OR



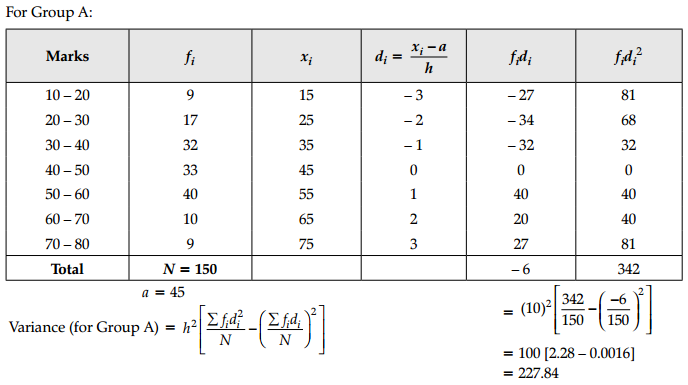
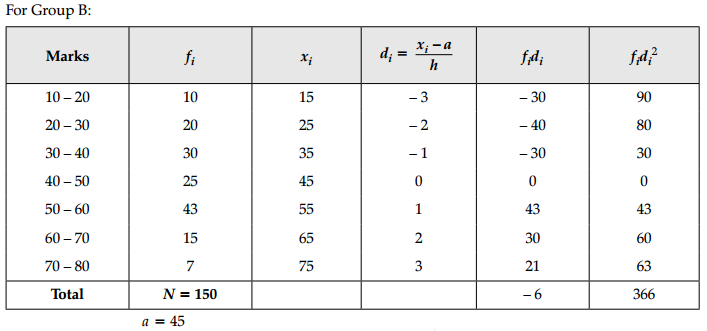
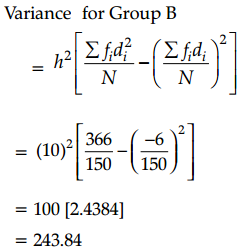
Since variance for Group B is more than that of A, so B is more variable than A.

Question 35.
In an automobile factory, certain parts are to be fixed into the chassis in a section before it moves into another section. On a given day, one of the three people A, B and C carries out this task. A has 45% chance, B has 35% chance and C has 20% chance of doing the task. The probability that A, B and C will take more than the allotted time is \(\frac{1}{6}\), \(\frac{1}{10}\) and \(\frac{1}{20}\), respectively. If it is found that the time taken is more than the allotted time, what is the probability that A has done the task.
Answer:
Let E₁, E₂ and E₃ denote the events of carrying out the tasks A, B and C, respectively.
Let H denote the event of taking more time.
Then, P(E₁) = 0.45, P(E₂) = 0.35 and P(E₃) = 0.20

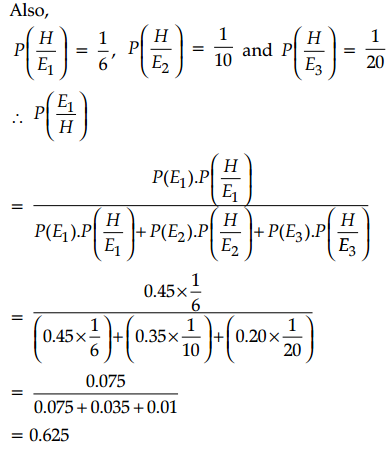
Section-E

(This section comprises 3 source-based questions (Case Studies) of 4 marks each)

Question 36.
In class of XI, teacher was describing logarithm to students. In logarithm, he states two properties which are as mentioned below:

Fundamental Laws of Logarithms
Law 1: Logarithm of the product of two numbers is equal to the sum of the logarithms of the numbers to the same base,
i.e., log_a mn = log_a m + log_a n
Law 2: The logarithm of the quotient of two numbers is equal to the difference of their logarithms to the same base,
i.e., \(\log _a\left(\frac{m}{n}\right)\) = log_a m – log_a n
On the basis of this information answer the following questions:
(i) Find the value of log 5 + log 2 is equal to
OR
Find the value of \(\log \frac{10}{2}+\log \frac{22}{11}\).
(ii) Evaluate: \(\log \frac{25}{27}+\log \frac{81}{125}+\log \frac{25}{3}\).
(iii) If log x + log y = log (x + y), then find the relation between x and y.
Answer:
(i) log 5 + log 2 = log(5 × 2)
= log 10
= 1

(ii) \(\log \frac{25}{27}+\log \frac{81}{125}+\log \frac{25}{3}=\log \left(\frac{25}{27} \times \frac{81}{125} \times \frac{25}{3}\right)\) = log 5

(iii) Given, log x + log y = log (x + y)
⇒ log (x.y) = log (x + y) [∵ Applying rule log_a (mn) = log_a m + log_a n]
⇒ xy = x + y
⇒ xy – y = x
⇒ y(x – 1) = x
⇒ y = \(\frac{x}{x-1}\)

Question 37.
Roshan invested ₹ 50000 in bank at the rate of 10% per annum compounded annually.

On the basis of this information, answer the following questions:
(i) What will be the interest for the first year?
(ii) What will be the interest for the second year?
(iii) After three years, how much amount Roshan will get on the given rate of interest compounded annually?
OR
Find the difference between the simple interest and compound interest for first two years.
Answer:
(i) Interest for the first year is given by
I = \(\frac{P R T}{100}\)
= \(\frac{50000 \times 10 \times 1}{100}\)
= 5000

(ii) We know that, A = \(P\left(1+\frac{r}{100}\right)^n\)
where P is the principal and A is the amount received and n is number of years and r is rate of interest.
Interest for the first year = ₹ 5000
Principal for the second year will be ₹ 55000.
Therefore, interest for the second year = \(\frac{55000 \times 10 \times 1}{100}\) = ₹ 5500
(iii) Compound interest for third year = \(\frac{60500 \times 1 \times 10}{100}\) = ₹ 6050
Therefore, total interest after three years = 5000 + 5500 + 6050 = ₹ 16550
Total amount = ₹ 50000 + ₹ 16550 = ₹ 66500
OR
Simple interest for two years = \(\frac{50000 \times 2 \times 10}{100}\) = ₹ 10000
Compound interest for two years = ₹ 5000 + ₹ 5500 = ₹ 10500
Therefore, difference = 10500 – 10000 = ₹ 500

Question 38.
Each side of an equilateral triangle is 24 cm. The mid-point of its sides are joined to from another triangle. This process is going continuously infinite.

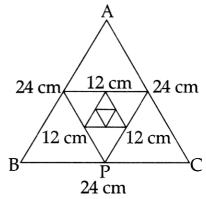
Based on the above information, answer the following questions:
(i) Find the side of the 5th triangle (in cm). Also, find the area of all the triangles.
OR
(ii) Find the sum of perimeter of first 6 triangles (in cm). Also, find sum of perimeter of all triangles (in cm).
Answer:
(i) The side of first triangle = 24 cm
Side of second triangle = 24 ÷ 2 = 12 cm
Similarly, side of third triangle = 12 ÷ 2 = 6 cm
Side of fifth triangle, a₅ = ar⁴
= \(24\left(\frac{1}{2}\right)^4\)
= 24 × \(\frac{1}{16}\)
= \(\frac{3}{2}\)
= 1.5 cm
Area of first triangle = \(\frac{\sqrt{3}}{4} \times(24)^2\)
= √3 × \(\frac{576}{4}\)
= 144√3
Area of second triangle = \(\frac{\sqrt{3}}{4} \times(12)^2\)
= √3 × \(\frac{144}{4}\)
= 36√3
Sum of area of all triangles

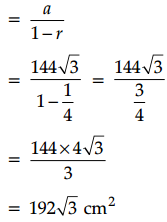
OR
(ii) Perimeter of first triangle = 24 × 3 = 72 cm
Perimeter of second triangle = 12 × 3 = 36 cm
∴ Sum of perimeter of first 6 triangles,

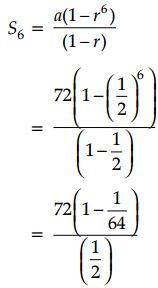
= \(\frac{72 \times \frac{63}{64}}{\frac{1}{2}}\)
= \(\frac{567}{4}\)
Now, Sum of perimeter of all triangles = 3(24 + 12 + 6 + ……)
= \(3\left(\frac{24}{1-\frac{1}{2}}\right)\)
= \(3 \times \frac{24}{\frac{1}{2}}\)
= 3 × 24 × 2
= 144 cm