Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 8 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 8 with Solutions
Time : 2 Hours.
Max. Marks : 40
General Instructions :
- The question paper consists of 14 questions divided into three Sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section – A
Question 1.
The 4th term of an A.P. is equal to 3 times the first term and 7th term excess with the 3rd term by 1. Find its nth term. (2)
Solution:
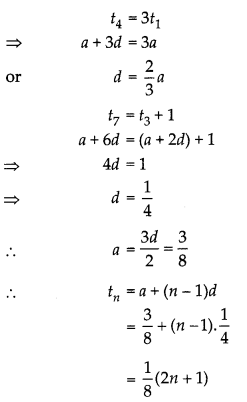
Question 2.
If the quadratic equation px² – 2\(\sqrt{5}\) px + 15 = 0, has two equal roots then find the value of p. (2)
Solution:
The given quadratic equation is,
px² – 2\(\sqrt{5}\) px + 15 = 0
This equation is of the form
ax² + bx + c = 0
where, a = p,b = – 2\(\sqrt{5}\) p, c = 15
We know, D = b² – 4ac
= (- 2\(\sqrt{5}\)p)² – 4 x p x 15
= 20p² – 60p
= 20p (p-3)
For real and equal roots, we must have
D = 0 ⇒ 20p (p – 3) = 0
⇒ p = 0, p = 3
p = 0, is not possible as whole equation will be zero.
Hence, 3 is the required value of p.
Question 3.
In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then find the ∠BOC. (2)
Solution:
Given, AB = AC, OB = OC and ∠A = 40°
Join AO such that it is perpendicular to the chord BC and bisects ∠A.
Thus, ∠BAO = ∠OAC = 20°
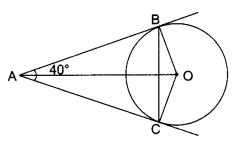
Also, as OB and OC are perpendicular to AB and AC respectively.
∴ ∠ABO = ∠ACO = 90°
Now, in ∆ ABO,
∠BOA = 180° – (90° + 20°)
or ∠BOA = 180° – 110° = 70°
Similarly in ∆ACO,
∠COA = 180° – (90° + 20°)
or ∠COA = 180° – 110° = 70°
Hence, ∠BOC = ∠BOA + ∠COA
= 70° + 70° = 140°.
Question 4.
The diameter of a sphere is 6 cm. It is melted and drawn in to a wire of diameter 2 mm. Find the length of the wire. (2)
Solution:
∴ Diameter of sphere = 6 cm
Radius (r) = \(\frac {6}{2}\) = 3 cm
Volume = \(\frac {4}{3}\) πr³ = (3)³ cm³
= \(\frac {4}{3}\)π x 3 x 3 x 3
= 36π cm³
Diameter of wire = 2 mm
∴ Radius (r2) = \(\frac {2}{2}\) = 1 mm = \(\frac {1}{10}\) cm
Let h be its length, then

Question 5.
Consider the following distribution: (2)
| Marks obtained | Number of students |
| More than or equal to 0 | 63 |
| More than or equal to 10 | 58 |
| More than or equal to 20 | 55 |
| More than or equal to 30 | 51 |
| More than or equal to 40 | 48 |
| More than or equal to 50 | 42 |
Find the frequency of the class 30 – 40.
Solution:
| Marks obtained | Number of students |
| 0-10 | (63 – 58) = 5 |
| 10-20 | (58 – 55) = 3 |
| 20-30 | (55 – 51) = 4 |
| 30-40 | (51 – 48) = 3 |
| 40-50 | (48 – 42) = 6 |
| 50-60 | 42 = 42 |
The frequency of the class interval 30-40 is 3.
Question 6.
If the roots of the equation \((a-b) x^{2}+(b-c) x+(c-a)=0\) are equal, prove that b + c = 2a.
OR
Find the value of k for which the equation \(x^{2}+k(2 x+k-1)+2=0\) has real and equal roots. (2)
Solution:
Given \((a-b) x^{2}+(b-c) x+(c-a)=0\)
Comparing with \(A x^{2}+B x+C=0\), we get
A = a-b, B = b- c and C = c – a
Since the roots are equal
∴ D = 0
⇒ B² – 4AC = 0
⇒ (b – c)² – 4(a – b)(c – a) = 0
⇒ b² + c² – 2be – 4(ac – bc – a² + ab) = 0
⇒ b² + c² – 2bc – 2ac + 4bc + 4a² – 4ab = 0
⇒ b² + c² + 4a² + 2bc – 4ac – 4ab = 0
⇒ (b + c – 2a)² = 0
⇒b + c – 2a = 0
⇒ b + c = 2a.
Given equation is,
x² + k(2x + k – 1) + 2 = 0
⇒ x² + 2kx + k(k – 1) + 2 = 0
Here a = 1, b = 2k and c = k(k – 1) + 2
For real and equal roots
b² – 4ac = 0
⇒ (2k)² – 4.1. (k (k – 1) + 2) = 0
⇒ 4k² – 4(k² – k + 2) = 0
⇒ 4k² – 4k² + 4k – 8 = 0
⇒ 4k = 8
⇒ k = \(\frac { 8 }{ 4 }\) =2
Section – B
Question 7.
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes. (3)
| Number of mangoes | 50-52 | 53-55 | 56-58 | 59-61 | 62-64 |
| Number of boxes | 15 | 110 | 135 | 115 | 25 |
Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
OR
If the median of the following frequency distribution is 32.5. Find the values \(f_{1}\) and \(f_{2}\).
| Class | Frequency |
| 0 – 10 | f1 |
| 10 – 20 | 5 |
| 20 – 30 | 9 |
| 30 – 40 | 12 |
| 40 – 50 | h |
| 50 – 60 | 3 |
| 60 – 70 | 2 |
Answer:
| C.I. | fi | (xi) | di = xi – 75 | fidi |
| 50 – 52 | 15 | 51 | – 6 | – 90 |
| 53 – 55 | 110 | 54 | – 3 | – 330 |
| 56 – 58 | 135 | 57 = A | 0 | 0 |
| 59 – 61 | 115 | 60 | 3 | 345 |
| 62 – 64 | 25 | 63 | 6 | 150 |
| ∑fi = 400 | ∑fidi = 75 |

Question 8.
Draw two tangents to a circle of radius 3.5 cm, from a point P at a distance of 6.2 cm from its centre. (3)
Answer:
Steps of construction:
Step I: Draw a circle of radius 3.5 cm taking O as a centre.
Step II: Take a point P at distance of 6.2 cm from the centre.
Step III: Draw a bisector of OP which intersect OP at C.
Step IV : From C, of radius OC draw a circle which intersect the previous circle at A and B.
Step V : Join AP and BP.
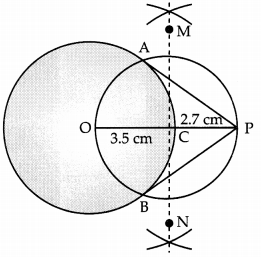
OP = OC + CP
= 3.5 + 2.7 = 6.2 cm
Hence AP and PB are the required tangents.
Question 9.
The arithemetic mean of the following frequency distribution is 53. Find the value of k. (3)
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80 -100 |
| Frequency | 12 | 15 | 32 | k | 13 |
Answer:
Given, Mean = 53
| Class | Frequency (fi) |
Mid-value (xi) |
fixi |
| 0-20 | 12 | 10 | 120 |
| 20-40 | 15 | 30 | 450 |
| 40-60 | 32 | 50 | 1600 |
| 60-80 | k | 70 | 70k |
| 80 -100 | 13 | 90 | 1170 |
| 72 + k | 3340 + 70k |
Mean = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
53 = \(\frac{3340+70k}{72+k}\)
⇒ 53(72 + k) = 3340 + 70k
⇒ 3816 + 53k k = 3340 + 70k
⇒ k = 28
Question 10.
An aeroplane when flying at a height of H m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the point on the ground are θ and Φ respectively. Prove that the vertical distance between the two planes is \(\frac{H(\tan \theta-\tan \phi)}{\tan \theta}\). (3)
Answer:
Let AB be the distance between the two planes and D be the point of observation on the ground.
So AB = h m
Let BC be the height of the second plane from the ground and BC = (H – h) m
Now, in ΔBDC,
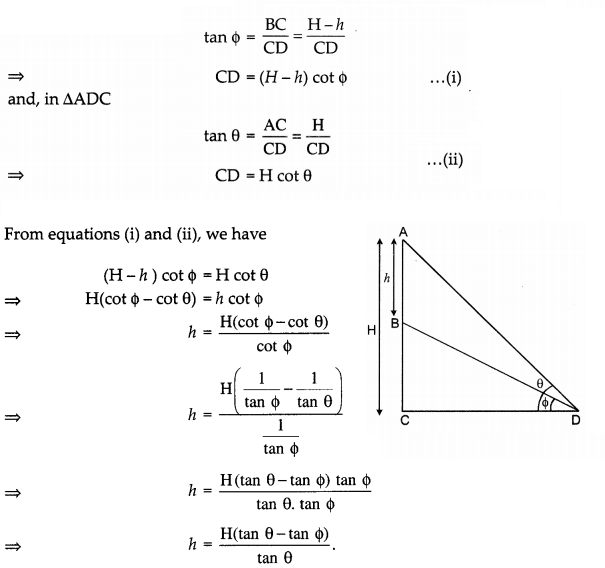
Hence Proved.
Section – C
Question 11.
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right-circular cone mounted on a hemisphere. Find the radius of the hemisphere if the height of the cone is 3 times the radius.
OR
Six tennis balls of diameter 62 mm are placed in cylindrical tube. Find the volume of the six balls and the internal volume of unfilled space in the tube and express this as a percentage of the volume of the tube. (4)

Solution:
Given, Diameter of the cylinder = 12 cm
∴ Radius = 6 cm
Height of the cylinder = 15 cm
Number of toys = 12
Let the radius of the hemisphere be r cm
Thus, Height of the cone = 3r cm
Now, Volume of cylinder = n(6)² 15 cm³
= (36) (15)TI cm³
= 54071 cm³
Now, Total volume of 12 toys =12 [Volume of cone + Volume of hemisphere]
Thus, Total volume of 12 toys = \(12\left[\frac{1}{3} \pi 3 r(r)^{2}+\frac{2}{3} \pi r^{3}\right] \mathrm{cm}^{3}\)
= 4[3πr³ + 2πr³] cm³
= 20πm³ cm³
Now, 20πr³ = 540π
⇒ r³ =2 7
⇒ r³ = (3)³
⇒ r = 3 cm
Thus, Radius of the hemisphere = 3 cm
OR
Diameter of the tennis balls = 62 mm.
∵ Radius of the balls and tube is half the diameter
∴ r = \(\frac { 1 }{ 2 }\) x 62 = 31 mm
Volume of one ball = \(\frac { 4 }{ 3 }\) πr³
= \(\frac { 4 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x 31 x 31 x 31
= 124,838.476 mm³
= 124.838 cm³
Question 12.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle. (4)
Answer:
Let C1 and C2 be the two circles having same centre O.
And, AC is a chord which touches the circle C: at point D.
Join OD, So, OD ⊥ AC
[Since, perpendicular from centre bisects the chords]
AD = DC = 4 cm
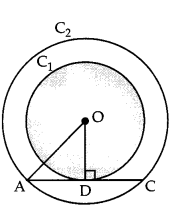
Thus, in right angled AAOD,
∴ OA² = AD² + DO²[By Pythagoras theorem]
⇒ DO² = 52 – 42 = 25 – 16 = 9
⇒ DO = 3 cm
Therefore, the radius of the inner circle, OD = 3 cm.
Question 13.
One day while sitting on the bridge across a river Aaradhya observes the angles of depression of the banks on opposite sides of the river to be 30° and 60° respectively as shown in the figure. (4)
(Take \(\sqrt{3}\) = 1.73)
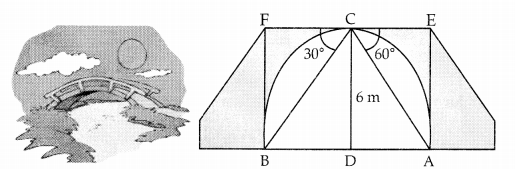
Based on the above information, answer the following questions :
(i) If the bridge is at a height of 6 m, then find AD.
(ii) What is the width of the river?
Solution:

Question 14.
India is competitive manufacturing location due to the low cost of manpower and strong technical and engineering capabilities contributing to higher quality production runs. (4)

The production of TV sets in a factory increases uniformly by a fixed number every year. It produced 16000 sets in 6th year and 22600 in 9th year.
Based on the above information, answer the following questions :
(i) Find the production for first year.
(ii) In which year, the production is ₹ 29,200.
Solution:
and a6 = 16000
and a9 = 22600
Since, an = a + (n – 1)d
⇒ a6 = a + 5d = 16000 … (i)
and a9 = a + 8d = 22600 … (ii)
Solving equations (i) and (ii), we get
d = 2200
and a = 5000
∴ It produced 5000 sets in 1st year
(ii) Given, an = 29200
⇒ a + (n – 1)d = 29200
⇒ 5000 + (n – 1)2200 = 29200
⇒ (n – 1)2200 = 24200
⇒ n = 12