CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 7 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 7 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 7 with Solutions

Time : 2 Hr.
Max. Marks : 40

General Instructions :

• The question paper consists of 14 questions divided into three Sections A, B, C.
• All questions are compulsory.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Section – A

Question 1.
Calculate the value of p from the following data: (2)

Class	Frequency
0-20	8
20-40	15
40-60	P
60-80	12
80 -100	5
	N = ∑fi = 60

Solution:
Given, N = ∑f_i = 60
⇒ 8 + 15 + p + 12 + 5 = 60
⇒ 40 + p = 60
⇒ p = 20.

Question 2.
If the roots of the equation (a² – bc)x² + 2(b² – ac)x + (c² – ab) = 0 are equal, where b ≠ 0, then find the relation between a, b and c. (2)
OR
If 3 is a root of the equation kx² – kx – 3 = 0, find then the value of k. (2)
Solution:
(a² – bc)x² + 2(b² – ac)x + (c² – ab) = 0
The given roots are equal, and then D must be zero
[2(b² – ac)]² – 4(a² – bc)(c² – ab) = 0
⇒ 4(b⁴ + a²c² – 2ab²c) – 4(a²c² – a³b – bc³ + ab²c) = 0
⇒ Ab⁴ – 12ab²c + 4bc³ + 4a³b = 0
⇒ 4b(b³ – 3abc + c³ + a³) = 0
⇒ a³ + b³ + c³ – 3abc = 0
⇒ a³ + b³ + c³ = 3 abc
OR
If 3 is the root of kx² – kx – 3 = 0 then 3 satisfy it i.e.,
9k – 3k – 3 = 0
⇒ 6k – 3 = 0
⇒ 6k = 3
⇒ k = \(\frac { 3 }{ 6 }\)
⇒ k = \(\frac { 1 }{ 2 }\)

Question 3.
The surface area of two spheres are in the ratio 16 : 9. Find the ratios of their volumes. (2)
Solution:
Let the radius of the larger sphere be R and the smaller be r.
Given, 4πR² : 4π² = 16 : 9
⇒ R² : r² = 4² : 3²
⇒ R : r = 4 : 3
Thus, \(\mathrm{V}_{1}: \mathrm{V}_{2}=\frac{4 \pi}{3} \mathrm{R}^{3}: \frac{4 \pi}{3} r^{3}=4^{3}: 3^{3}\)
or V₁ : V₂ = 64 : 27

Question 4.
The sum of first 20 odd natural numbers. (2)
Solution:
The given A.P. is
1, 3, 5, 7, 9,11,13,15,17,19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39
Thus
a = 1, d = 2 and n = 20
We know that,
S_n = \(\frac { n }{ 2 }\){2a + (n – 1)d}
= \(\frac { 20 }{ 2 }\) {2(1)+ (20 – 1)2}
= 10{2 + 38} = 400.

Question 5.
In the given figure, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA is perpendicular to PB,„then find the length of each tangent. (2)
Solution:
Now, AP = BP [Since, tagnents from an external point P are equal]
Join CA and CB and they are perpendicular to AP and AB respectively.

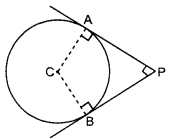
Given CA = CB = 4 cm (Radius of circle)
Now, ∠ACB = 360° – [90° + 90° + 90°]
or ∠ACB = 90°
As APBC is a right-angled quadrilateral with its adjacent sides CA and CB being 4 cm.
So AP = PB = 4 cm
[Opposite sides to adjacent sides of a right-angled quadrilateral]

Question 6.
If the zeros of the quadratic equation x² + (a + 1)x + b + 1 = 0 are 2 and – 3, then find the values of a and b. (2)
Solution:
If 2 and – 3 are the roots of x² + (a +1) x + b +1 = 0 then they satisfy this equation.
4 + (a + 1)² + b + 1 = 0
⇒ 4 + 2a + 2 + b + 1 = 0
⇒ 2a + b + 7 = 0
⇒ 2 a + b = – 7
also, 9 – 3(a + 1) + b + 1 = 0
9 – 3a – 3 + b + 1 = 0
– 3a + b + 7 = 0
– 3a + b = – 7
On subtracting (1) from (2), we get
– 5a = 0
⇒ a = 0
Putting a = 0 in equation (1), we get b = – 7
Hence a and b are 0 and – 7.

Section – B

Question 7.
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other. (3)
Solution:
Steps of constructions:

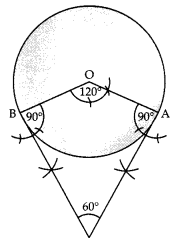
Step I: Draw a circle with O as center and radius 4 cm.
Step II: Draw any ∠AOB = 120° (180° – 60°)
Step III: From A and B draw ∠PAO = ∠PBO = 90° which meet at P.
∴ PA and PB are the required tangents.
Hence ∠BPA = 60°, as PBOA is a cyclic quadrilateral.

Question 8.
The following tables gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate. (3)

Literacy rate (in %)	45-55	55-65	65-75	75-85	85-95
Number of cities	3	10	11	8	3

Solution:

Litracy rate (in %)	Number of cities (fi)	Class mark (xi)	di = xi – 70	fidi
45 – 55	3	50	– 20	– 60
55 – 65	10	60	– 10	– 100
65 – 75	11	70 = A	0	0
75 – 85	8	80	10	80
85 – 95	3	90	20	60
				∑fidi= – 20

Here, we have
\(\bar { x }\) = \(\mathrm{A}+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}=70-\frac{20}{35}\)
= 70 – 0.57 = 69.43

Question 9.
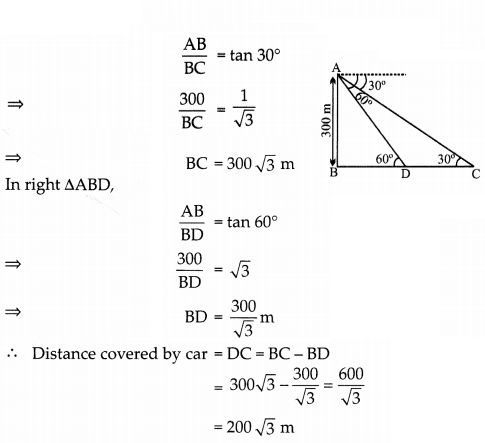
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds, the angle of elevation become 30°. If the aeroplane is flying at a constant height of 3000 \(\sqrt{3}\) m, find the speed of the aeroplane. (3)
OR
A highway leads to the foot of 300 m high tower. An observatory is set at the top of the tower. It sees a car moving towards it at an angle of depression of 30°. After 15 seconds, angle of depression becomes 60°. Find the distance travelled by the car during this time.
Solution:
Let the ground distance between the aeroplane A and the point E be x m.
Given, height AD is 3000\(\sqrt{3}\) m and the angle of elevation is 60°.
So, in ∆AED,

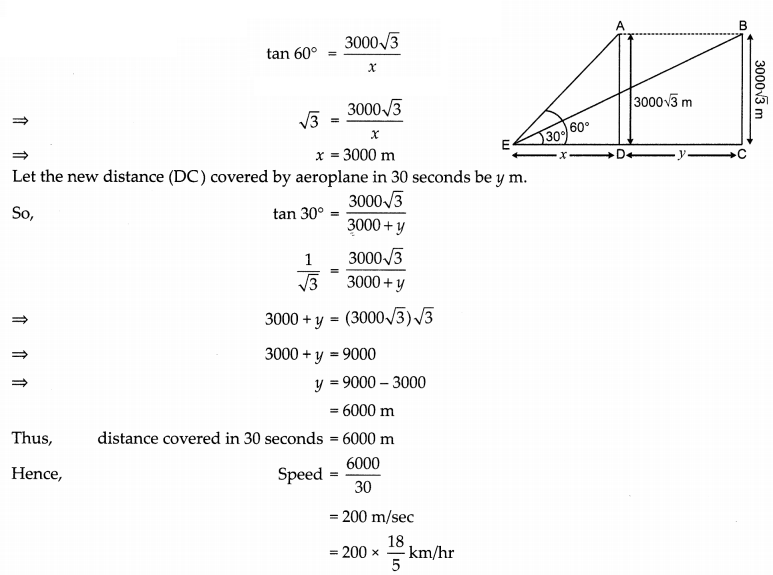
Hence, the speed of the aeroplane is 720 km/hr.
OR
Let AB = 300 m is the tower. Initially, car is at C and after 15 seconds, it reaches at D.
In right ∆ABC,

Question 10.
Mode of the following frequency distribution is 65 and sum of all the frequencies is 70. Find the missing frequencies x and y. (3)

Class Interval	0-20	20-40	40 – 60	60-80	80 – 100	100 – 120	120 – 140	140 – 160
Frequency	8	11	x	12	y	9	9	5

Solution:

Class Interval	Frequency
0-20	8
20-40	11
40-60	x(fo)
60-80	12(f1)
80 -100	y(f2)
100 -120	9
120 -140	9
140 -160	5
	∑f = 70

Here, 8 + 11 + x + 12 + y + 9 + 9 + 5 = 70 [Given]
⇒ 54 + x + y = 70 … (i)
⇒ x + y = 70 – 54 = 16
Mode = 65 [Given]
∴ Modal Class is 60 – 80
So, l = 60, h = 20, f_o = x, f₁ = 12, f₂ = y

Section – C

Question 11.
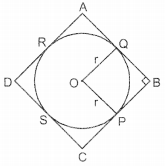
In the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B = 90°. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the value of radius (r). (4)

Solution:
Given, ∠B = 90°, AD = 23 cm, AB = 29 cm, DS = 5 cm and OQ = OP = r.
Now, DS = DR = 5 cm [Tangents from point D]
Thus, AR = AD – DR
= (23 – 5) cm = 18 cm
Hence, AQ = 18 cm [Tangents from point A]
or BQ = AB – AQ
= (29 – 18) cm = 11 cm
Also, ∠OQB = ∠OPB = 90° [Both the radii are perpendicular to tangents AB and BC respectively]
Hence, in the quadrilateral POQB,
∠QOP = 360° – (90° + 90° + 90°)
= 360° – 270° = 90°
In quadrilateral POQB,
∠QOP = ∠OPB = ∠PBQ = ∠BQO = 90°
and BQ = PB [Tangents from point B]
i.e. all angles are 90° and adjacent sides are equal.
Hence, POQB is a square
∴ OQ = BQ = 11 cm
But OQ = OP
So, OQ = OP = PB = QB = 11 cm
Thus, the radius of the circle is 11 cm.

Question 12.
A well of diameter 4 m is dug 14 m deep. The earth taken out is spread evenly all around the well to form a 40 cm high embankment. Find the width of the embankment. (4)
OR
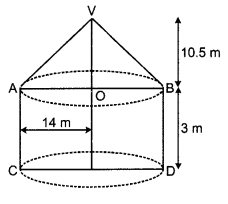
A tent is in the form of a right circular cylinder of base radius 14 m and height 3 m is surmounted by a right circular cone of the same base radius. The total height of the tent is 13.5 m. Find the cost of the canvas used in making the tent at ₹ 80 per square meter and the cost of painting it at ₹ 2 per square meter. [Use π = \(\frac { 22 }{ 7 }\)]
Solution:
We have, diameter of well = 4 m
∴ Radius, r = 2 m
and Height, h = 14 m.
Volume of earth taken out after digging the well
= πr²h
= \(\frac { 22 }{ 7 }\) x 2 x 2 x 14
= 176 m³
Let x be the width of the embankment formed by the earth taken out.
Then, volume of embankment
⇒ \(\frac { 22 }{ 7 }\) [(2 + x)² – (2)²] = 176
⇒ \(\frac { 22 }{ 7 }\)[4 + x² + 4x – 4] x \(\frac { 2 }{ 5 }\) = 176
⇒ \(x^{2}+4 x=\frac{176 \times 5 \times 7}{22 \times 2}\)
⇒ x² + 4x – 140 = 0
⇒ x² + 14x – 10x – 140 = 0
⇒ x(x + 14) – 10(x + 14) = 0
⇒ (x + 14) (x – 10) = 0
⇒ x = – 14 or 10
x = – 14(neglect)
∴ x = 10
Hence, width of embankment = 10 m.
OR
Given, height of the cylindrical structure = 3 m
Total height of the tent = 13.5 m
Base radius of cylindrical structure Base radius of conical structure = 14 m
Rate of canvas = ₹ 80 per m²
Rate of painting = ₹ 2 per m²
Now, height of the conical structure = (13.5 – 3) m = 10.5 m
∴ Total surface area of the tent = Curved surface area of the (cylindrical structure + conical structure)

= 2πrh + πrl
= πr (2h + 1)
= π(14)[latex]\sqrt{(14)^{2}+(10.5)^{2}}[/latex] m²
= π(14)(6 + \(\sqrt{196+110.25}\)) m²
= (14)π(6 + \(\sqrt{306.25}\)) m²
= (14)\(\frac { 22 }{ 7 }\)(6 + \(\sqrt{17.5}\)²)m²
= 44(6 + 17.5) m²
= 44 x 23.5 m² = 1034 m²
Thus, the cost of canvas = ₹ (80 x 1034)
= ₹ 82720
and, the cost pf pointing = ₹ (2 x 1034)
= ₹ 2068.

Question 13.
Treasure Hunt Games: While playing a treasure hunt game, some clues (numbers) are hidden in various spots collectively forms an AP. If the number of the nth spot is 20 + An, then answer the following questions to help the player in spotting the clues. (4)

(i) Which number is on the (n – 2)tn spot?
(ii) Which spot is numbered as 116?
Solution:
(i) Number on (n – 2)^th spot = t_n-2 = 20 + 4(n – 2)
= 20 + 4n – 8 = 12 + 4n

(ii) Let n^th spot be numbered as 116.
∴ t_n = 116
⇒ 20 + 4n = 116
⇒ 4n = 96
⇒ n = 24

Question 14.
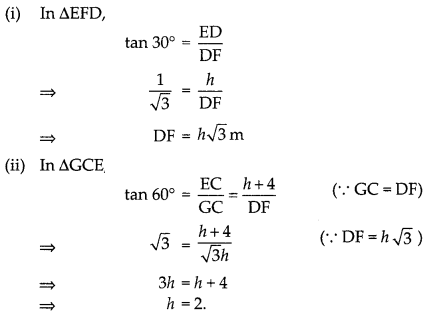
There are two windows in a house. First window is at the height of 2 m above the ground and other window is 4 m vertically above the lower window. Ankit and Radha are sitting inside the two windows at point G and F respectively. At an instant, the angle of elevation of a balloon from these windows are observed to be 60° and 30° as shown in the diagram: (4)

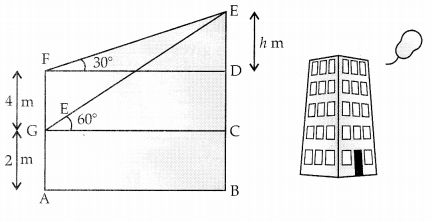
Answer the following questions.
(i) Find the value of DF.
(ii) What is the value of h in the given figure?
Solution: