CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 3 with Solutions

Time : 2 Hr.
Max. Marks : 40

General Instructions :

• The question paper consists of 14 questions divided into three Sections A, B, C.
• All questions are compulsory.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Section – A

Question 1.
For what values of k, the roots of the equation x² + 4x + k = 0 are real? (2)
Answer:
. The given equation is x² + 4x + k =0
On comparing the given equation with
ax² + bx + c = 0,
we get a = 1, b = 4 and c = k
For real roots, D ≥ 0
or b² – 4ac ≥ 0
16 – 4k ≥ 0
or k ≥ 4
∴ For k ≥ 4, equation x² + 4x + k will have real roots.

Question 2.
In the given figure, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then find ∠QOR. (2)

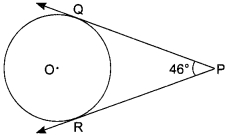
Prove that the line segment joining the points of contact of two parallel tangents of a circle passes through its centre.
Answer:
∠OPQ = ∠OPR = 23°
∠OQP = ∠ORP = 90°
∠QOP = ∠ROP
= 180° (90° + 23°)
= 180° – 113°
= 67°

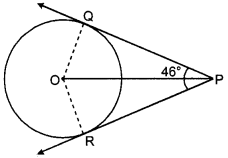
Hence ∠QOR = ∠QOP + ∠ROP
= 67° + 67° = 134°.
OR
Given, AC || DF
Let O be the centre of the circle. Join OB, OP, OE such that
OB – OP =OE = r
Also, let OP || BC || ED
Thus, ∠CBO + ∠BOP = 180°
or 90° + ∠BOP = 180°
or ∠BOP = 90°

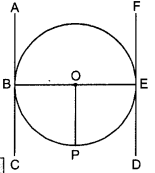
Similarly, ∠POE 90°
Thus, ∠BOE = ∠POE + ∠POB
= 90° + 90°
= 180°
Hence, BOF is a striaght line passing through the centre O.

Question 3.
From the following probability distribution, find the median class. (2)

Cost of living index	1400-1550	1550-1700	1700-1850	1850-2000
Number of weeks	8	15	21	8

Answer:

Cost of living index	No. of weeks (f)	c.f.
1400 – 1550	8	8
1550 – 1700	15	23
1700 – 1850	21	44
1850 – 2000	8	52
	∑f= 52

Here, N = 52
⇒ \(\frac {N}{2} = \frac {56}{2}\) = 26
26 will lie in the class interval 1700 – 1850.
∴ Median class is 1700 – 1850.

Question 4.
The first three terms of A.P. are (3y -1), (3y + 5) and (5y + 1). Then find y. (2)
Answer:
The terms of an A.P. are
(3y – 1), (3y + 5) and (5y + 1)
Thus, d = (3y + 5) – (3y – 1) – (5y + 1) – (3y + 5)
6 = 2y – 4
2y = 10
y = 5.

Question 5.
If k, 2k – 1 and 2k + 1 are three consecutive terms of an A.P., then find the value of k. (2)
Answer:
The terms of an A.P. are
k, (2k – 1) and (2k + 1)
Thus, d = (2k – 1) – k = 2k + 1 – (2k – 1)
2k – 1 – k = 2k + 1 – 2k + 1
k – 1 = 2
k = 3.

Question 6.
The diameter of the Moon is approximately one-fourth of the diameter of the Earth. What is the ratio (approximate) of their volumes ? (2)
Answer:
The diameter of Moon is approximately one-fourth of the diameter of Earth.
Let, Radius of Moon = r,
Then, Radius of Earth = 4r,
Required ratio = \(\frac { Volume of Moon }{ Volume of Earth }\)
= \(\frac{\frac{4}{3} \pi r^{3}}{\frac{4}{3} \pi(4 r)^{3}}\)
= \(\frac{r^{3}}{64 r^{3}}\)
= \(\frac{1}{64}\)
= 1 : 64

Section – B

Question 7.
Amit, standing on a horizontal plane, finds a bird flying at a distance of 200 m from him at an elevation of 30°. Deepak standing on the roof of a 50 m high building, finds the angle of elevation of the same bird to be 45°. Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak. (3)
Answer:
Let Amit be at C point and bird is at A point, such that LACB 300. AB is the height of bird from point B on ground and Deepak is at D point,
DE is the building of height 50 m.

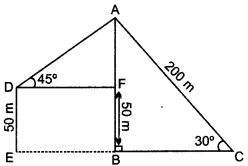
Now, in right iABC, we have
\(\sin 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{1}{2}=\frac{\mathrm{AB}}{200}\)
⇒ AB = 100 cm (AB = AF + BF, 100 = AF + 50, AF = 50)
In right ∆AFD, we have
\(\sin 45^{\circ}=\frac{A F}{A D}\)
⇒ \(\frac{1}{\sqrt{2}}=\frac{50}{\mathrm{AD}}\)
⇒ AD = \(50\sqrt{2}\)
Hence, the distance of bird from Deepak is \(50\sqrt{2}\) m.

Question 8.
The table below shows the distribution of marks obtained by students in an examination. Calculate the value of x, if the mean mark is 18.  (3)

Marks	5	10	15	20	25	30
No. of students	6	4	6	12	X	4

Given, Mean = 18

Marks (x)	No. of students (f)	f x x
5	6	30
10	4	40
15	6	90
20	12	240
25	x	25x
30	4	120
Total	32 + x	520 + 25x

Mean = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
or \(\Sigma f_{i} \times \text { Mean }=\Sigma f_{i} x_{i}\)
⇒ (32 + x)18 = 520 + 25x
or 520 + 25x = 576 + 18x
⇒ 25x – 18x = 576 – 520
⇒

Question 9.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm.  (3)
Answer:
Steps of construction:

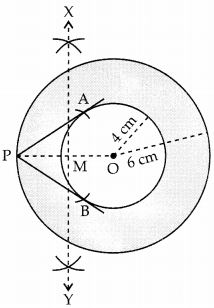
(1) Draw two concentric circles with centre O of radii 4 cm and 6 cm.
(2) Take a point P on the bigger circle of radius 6 an.
(3) Join OP with dotted line.
(4) Draw perpendicular bisector of OP which intersects OP at M.
(5) With P as centre and MP radius, mark two arcs on smaller circle of radius 4 cm at point A and B.
(6) Join PA and PB.
PA and PB are the required pair of tangents.

Question 10.
The following distribution shows the daily pocket allowance of children of a locality. If the mean pocket allowance is ? 18, find the missing frequency f.  (3)

Daily pocket allowance (in ₹)	11 – 13	13-15	15-17	17-19	19-21	21-23	23-25
Number of children	7	6	9	13	f	5	4

OR
To find out the concentration of S0² in the air (in parts per million i.e., ppm), the data was collected for 30 localities in a certain city and is presented below :

Concentration of S02 (in ppm)	0.00 – 0.04	0.04 – 0.08	0.08 – 0.12	0.12 – 0.16	0.16 – 0.20	0.20 – 0.24
Frequency	4	9	9	2	4	2

Find the mean concentration of S0² in the air.
Answer:
We have,

Daily pocket allowance (in ?)	Number of children (fi)	Mid-value of (xi)	(fi × xi)
11 – 13	7	12	84
13 – 15	6	14	84
15 – 17	9	16	144
17 – 19	13	18	234
19 – 21	f	20	20/
21 – 23	5	22	110
23 – 25	4	24	96
Total	∑fi = 44+f		\(\Sigma\left(f_{i} \times x_{i}\right)\) = 752 + 20/

Now,
Mean = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
⇒ 18 = \(\frac{752+20 f}{44+f}\)
⇒ 18(44 + f) = 752 + 20f
⇒ 18(44+ f) = 752 + 20f
⇒ 792 + 18f = 752 + 20f
⇒ 2f = 40
⇒ f = 20.
OR

Concentration of S02 (in ppm)	Frequency (f)	Class mark (xi)	di = (xi) – 0.14	fidi
0.00 – 0.04	4	0.02	– 0.12	– 0.48
0.04 – 0.08	9	0.06	– 0.08	– 0.72
0.08 – 0.12	9	0.10	– 0.04	– 0.36
0.12 – 0.16	2	0.14 = A	0	0
0.16 – 0.20	4	0.18	0.04	0.16
0.20 – 0.24	2	0.22	0.08	0.16

Here, we have ∑f = 30, ∑f_id = -1.24
and A = 0.14
\(\bar{x}=\mathrm{A}+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}=0.14+\frac{-1.24}{30}\)
= 0.14 – 0.041
= 0.99.

Section – C

Question 11.
The 16th term of an A.P. is five times its third term. If its 10th term is 41, then find the sum of its first fifteen terms. (4)
Answer:
Given that l6 term of an A.P. is five time its third term.
a + (16 – 1)d = 5[a + (3 – 1)d]
⇒ a + 15d = 5[a + 2d]
⇒ a + 15d = 5a + 10d
⇒ 4a – 5d = 0

Also given that,
T₁₀ = 41
⇒ a + (10 – 1)d = 41
⇒ a + 9d = 41
On multiplying equation (ii) by 4, we get
4a + 36d = 164
Subtracting equation (iii) from (j), we get

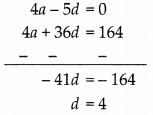
On substituting the value of d in (i), we get
4a – 5 x 4 = 0
⇒ 4a = 20
⇒ a = 5
Now
\(S_{15}=\frac{15}{2}[2 a+(15-1) d]\)
⇒ \(S_{15}=\frac{15}{2}(2 \times 5+14 \times 4)\)
\(\frac{15}{2} 2(5+14 \times 2)\)
= 15(5 + 28)
= 15 x 33
⇒ S₁₅ = 495

Question 12.
The shadow of a flagstaff is three times as long as the shadow of the flagstaff when the Sun rays meet the ground at an angle of 60°. Find the angle between the Sun rays and the ground at the time of longer shadow. (4)
OR
From an aeroplane vertically above a straight horizontal plane, the angles of depression of two consecutive kilometer stones on the opposite sides of the aeroplane are found to be a and . Show that the height of the aeroplane is \(\frac{\tan \alpha \cdot \tan \beta}{\tan \alpha+\tan \beta}\)
Answer:
Let AB be the flagstaff and BC be the length of its shadow when the Sun rays meet the ground at an angle of 600. Let O be the angle between the Sun rays and the ground when the length of the shadow of the flagstaff is BD. Let h be the height of the flagstaff.
Let BC = x
Then, BD = 3x and CD = 2x .
In ∆ACB, we have
\(\tan 60^{\circ}=\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ \(\sqrt{3}=\frac{h}{x}\)
⇒ \(h=\sqrt{3} x\)

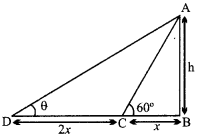
In ADB, we have
\(\tan \theta=\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ \(\tan \theta=\frac{h}{3 x}\)
⇒ \(\tan \theta=\frac{\sqrt{3} x}{3 x}\)
⇒ \(\tan \theta=\frac{1}{\sqrt{3}}\)
⇒ \(\tan \theta=\tan 30^{\circ}\)
⇒ tan θ = tan 30°
θ = 30°
OR
Let P be the position of plane, A and B be the positions of two stones one kilometer apart. Angles of depression of stones A and B are a and 3 respectively. Let PC = h km.
In right-angled ACP, we have,

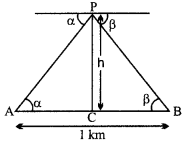
\(\tan \alpha=\frac{\mathrm{PC}}{\mathrm{AC}}=\frac{h}{\mathrm{AC}}\)
\(\mathrm{AC}=\frac{h}{\tan \alpha}\)
\(\tan \beta=\frac{P C}{C B}=\frac{h}{C B}\)
\(\mathrm{CB}=\frac{h}{\tan \beta}\)
Adding equations (j) and (ii), we get
\(\mathrm{AC}+\mathrm{CB}=\frac{h}{\tan \alpha}+\frac{h}{\tan \beta}\)
\(h\left(\frac{\tan \beta+\tan \alpha}{\tan \alpha \cdot \tan \beta}\right)\)
As it is given that
AC + CB = 1
\(1=h\left(\frac{\tan \beta+\tan \alpha}{\tan \alpha \cdot \tan \beta}\right)\)
\(h=\frac{\tan \alpha \cdot \tan \beta}{\tan \alpha+\tan \beta}\)

Question 13.
Read the following passage and answer the questions that follows :
There is a circular park of radius 24 m and a pole at a distance of 26 m from the centre of the park, as shown in the figure. From the pole, there are two paths PR and PQ, which are tangential to the park. (4)

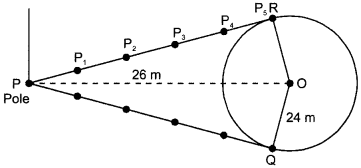
(i) Find the length of each path.
(ii) If five light poles are to be put along each tangential path at equal distances, find the distance between each consecutive light pole.
Answer:
(i) In right-angled triangle PRO
We have,
PR = .\(\sqrt{\mathrm{PO}^{2}-\mathrm{OR}^{2}}\)
= \(\sqrt{(26)^{2}-(24)^{2}}\)
= \(\sqrt{676-576}\)
= \(\sqrt{100}\)
= 10 m.

As PR and PQ are tangents from same external point so,
PR = PQ = 10 m.
(ii) Let the distance between consecutive poles be x.
Hence, 5x = 10
x = 2 m.
Each pole is at a distance of 2 m.

Question 14.
Vijay has rain water harvesting plant on his roof. After rain, all the water that is collected on the roof of 22 m x 20 m is drained into the cylindrical tank having diameter of base 2 m and height 3.5 m. It rained heavily last night and in the morning the tank is just full. (4)
(i) How much water is collected in the tank (in litres)?
(ii) Find the rainfall in cm.
Answer:
(i) We have,
Radius of cylindrical tank, r = \(\frac { 2 }{ 2 }\) = 1 m
Height of cylindrical tank, h = 3.5 m
Volume of cylindrical tank = r²h
= \(\frac{22}{7} \times(1)^{2} \times 3.5\)
=11 m³
Since, 1 m³ = 1000 lit
11 m³ = 11000 litres.
11000 litres of water is collected in tank.

(ii) Let the rainfall be x m,
∴  Volume of water = Volume of cuboid
=22 m × 20 m × x m.
= (22 × 20 × x) m³
= 440x m³
Since, the tank is just full of water that drains out of the roof into the tank.
∴  Volume of water = Volume of the cylindrical vessel
22 ³ 20 ³ x = 11
x = \(\frac { 11 }{ 440 }\)
\(\frac { 1 }{ 40 }\)
\(\frac { 100 }{ 40 }\)
= 2.5 cm.