CBSE Sample Papers for Class 10 Maths Standard Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Set 4 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 MCQs carrying 1 mark each
3. Section B has 5 questions carrying 02 marks each.
4. Section C has 6 questions carrying 03 marks each.
5. Section D has 4 questions carrying 05 marks each.
6. Section E has 3 case based integrated units of assessment (04 marks each) with sub parts of the values of 1, 1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2. Qs of 5 marks, 2.Qs of 3 marks and 2. Questions of 2. marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take n = 22/7 wherever required if not stated.

Section – A ( 20 Marks) 
Section A Consists of Multiple Choice Type questions of 1 mark each

Question 1.
The HCF of k and 93 is 31, where k is a number.
Which of these CAN be true for SOME VALUES of k?
(i) k is a multiple of 31
(ii) k is a multiple of 93
(iii) k is a an even number
(iv) k is a an odd number
(A) Only (ii) and (iii)
(B) Only (i), (i) and (iii)
(C) Only (i), (iii) and (iv)
(D) All (i), (ii), (iii) and (iv)
Solution:
(C) Only (i), (iii) and (iv)

Explanation: HCF of k and 93 = 31
It means Factor of 93 = 31 × 3
Factor of k = 31 × a
Thus, It is a multiple of 31, which can be even or odd.
Hence (i), (iii) and (iv) are correct.

Question 2.
If a semi-circle is rolled along its diameter, then the figure formed is [1]
(a) spherical
(b) conical
(c) cylindrical
(d) None of these
Answer:
(b) conical
When we roll a semi-circle along its diameter, a conical is formed.

Question 3.
What is the value of k such that the following pair of equations have infinitely many solutions?
x – 2y = 3 and -3x + ky = -9.
(A) -6
(B) -3
(C) 3
(D) 6
Solution:
(D) 6

Explanation: Given equations are:
x – 2y – 3 = 0
and -3x + ky + 9 = 0

⇒ 3k = 18 ⇒ k = 6
Hence, the value of k is 6.

Question 4.
The distance between two parallel tangents to a circle of radius 7 cm, is [1]
(a) 7 cm
(b) 0 cm
(c) 14 cm
(d) None of these
Answer:
(c) 14 cm

The distance between two parallel tangents to a circle of radius 7 cm is 2 × 7 = 14cm.

Question 5.
Which term of the progression 20, 19\(\frac{1}{4}\), 18\(\frac{1}{2}\), 17\(\frac{1}{3}\), is the first negative term:
(A) 27^th term
(B) 28^th term
(C) 26^th term
(D) 25^th term
Solution:
(B) 28^th term

Explanation: Here, d = \(\frac{-3}{4}\)
Let the n^th term be first negative term
∴ 20 + (n – 1)(\(\frac{-3}{4}\)) < 0
⇒ 3n = 83
⇒ n = 27\(\frac{2}{3}\)
Hence, 28^th term is first negative term.

Question 6.
HCF of two number is 23 and their LCM is 1449. If one of the number is 161, then the other number is [1]
(a) 207
(b) 307
(c) 1449
(d) None of these
Answer
(a) 207

Let the required number be x.
As, product of two numbers
= (HCF × LCM) of two numbers
∴ x × 161 = 23 × 1449
⇒ x = \(\frac{23 × 1449}{161}\) = 207

Question 7.
If the vertices of a parallelogram PQRS taken in order are P(3, 4), Q(-2, 3) and R(-3, -2), then the co-ordinates of its fourth vertex S are
(A) (-2, -1)
(B) (-2, -3)
(C) (2, -1)
(D) (1, 2)
Solution:
(C) (2, -1)

Explanation: Given PQRS is a parallelogram and diagonal PR and QS bisect each other at O.
Let fourth vertex be S(x, y), then

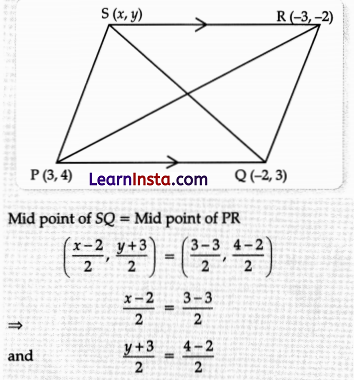
⇒ x – 2 = 0
⇒ x = 2
and y + 3 = 2
⇒ y = -1
Hence, co-ordinates of fourth vertex S are (2, -1).

Question 8.
If ∆ADE ~ ∆ACB, ∠DEC = 105° and ∠ECB = 65°, then the value of x is [1]
(a) 60°
(b) 90°
(c) 30°
(d) 40°
Answer:
(d) 40°

In ∆ADE and ∆ACB,
∵ ∆ADE ~ ∆ACB [given]
∴ ∠ACB = ∠ADE = 65°
Also, ∠AED = ∠ABC = 180° – 105° = 75°
In ∆ADE, ∠ADE + ∠AED + ∠DAE = 180°
⇒ 65° + 75° + ∠DAE =180°
⇒ ∠DAE = 180° – 140° = 40°

Question 9.
Ankit joins the centre of the two pulleys and observes line segments P₁S₁ and P₂S₂ when extended meet at a point X. Which line segment is equal to the length of P₁S₁?

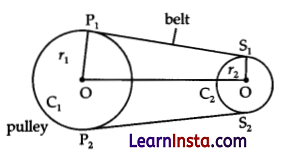
(A) OQ
(B) QX
(C) XS₂
(D) P₂S₂
Solution:
(D) P₂S₂

Explanation: The lengths of a tangent drawn from an external point to a circle are equal.
∴ P₂S₂ is equal to the length of P₁S₁.

Question 10.
Two numbers are in the ratio of 15 : 11. If their HCF is 13, then the numbers will be [1]
(a) 195 and 143
(b) 190 and 140
(c) 185 and 163
(d) 185 and 143
Answer:
(a) 195 and 143

Let the required numbers be 15x and 11x.
Then, their HCF is x, so x = 13
[∵ given HCF = 13]
∴ The numbers are 15 × 13 and 11 × 13 i.e. 195 and 143.

Question 11.
If x tan 60° cos 60° = sin 60° cot 60°, then x =
(A) cos 30°
(B) tan 30°
(C) sin 30°
(D) cot 30°
Solution:
(B) tan 30°

Explanation:
x tan 60° cos 60° = sin 60° cot 60°

Question 12.
If the point P(k, 0) divides the line segment joining the points A(2, – 2) and B(-7, 4) in the ratio 1:2, then the value of k is [1]
(a) 1
(b) 2
(c) – 2
(d) -1
Answer:
(d) -1

When a point P(x, y) divides (internally) the line segment joining the points A(x₁, y₁) and B(x₂, y₂) in the ratio m : n, then by section-formula

Question 13.
In the figure below, what is the length of AB?

(A) 45√3 m
(B) \(\frac{45}{\sqrt{3}}\)m
(C) 45(√3-1)m
(D) 45(√3 +1)m
Solution:
(C) 45(√3-1)m

Explanation: According to figure

Question 14.
Gayatri was making a mathematical model, in which she placed 4 cubes each of edge 20 cm one above the other. Then, the surface area of the resulting cuboid is
(a) 7000 cm²
(b) 7200 cm²
(c) 6000 cm²
(d) 7250 cm²
Answer:
(b) 7200 cm²

Given, edge of a cube is 20 cm.
The dimensions of the cuboid when 4 cubes each of edge 20 cm are placed one above another.
Length of the cuboid (l) = 20 cm
Breadth of the cuboid (b) = 20 cm
and Height of the cuboid (h) = 20 + 20 + 20 + 20
= 80 cm
∴ Surface area of the resulting cuboid formed = 2 (lb + bh + hl)
= 2(20 × 20 + 20 × 80 + 80 × 20)
= 2(400 + 1600 + 1600)
= (2 × 3600) = 7200 cm²

Question 15.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is:
(A) 31 cm
(B) 25 cm
(C) 62 cm
(D) 50 cm
Solution:
(D) 50 cm

Explanation: Let r₁ = 24 cm and r₂ = 7 cm
Area of first circle = πr₁² = π(24)² = 576π cm²
Area of second circle = πr₂² = π(7)² = 49π cm²
According to question,
Area of circle = area of first circle + area of second circle
πR² = 576π + 49π [where, R be radius of circle]
R² = 625 ⇒ R = 25 cm
Diameter of a circle = 2R = 2 × 25 = 50 cm.

Question 16.
Which of the following is a measure of central tendency?
(a) Frequency
(b) Cumulative frequency
(c) Mean
(d) Class-limit
Answer:
(c) Mean

Mean is a measure of central tendency.

Question 17.
This is a paper cup.

Jaya tossed this cup.
When the cup lands on the table, it can land in three possible positions, as shown below.

To calculate the probability of falling in each position, Jaya tosses the cup 60 times.
She records her observations in the table below.

Position of cup after toss	Frequency
Inverted	20
upright	5
Rolling side	35

Jaya tosses the cup one more time.
What would be the probability of the cup falling in the upright position?
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{11}\)
(C) \(\frac{1}{12}\)
(D) \(\frac{1}{60}\)
Solution:
(C) \(\frac{1}{12}\)

Explanation: Total number of outcomes = 60
Possible outcomes of upright position = 5
∴ Required probability = \(\frac{5}{60}\) = \(\frac{1}{12}\)

Question 18.
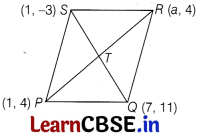
A parallelogram has vertices P(1, 4), Q(7, 11), R(a, 4) and S(1, -3). Then, the value of a is [1]
(a) 6
(b) 7
(c) 5
(d) 4
Answer:
(b) 7

Let P(1, 4), O(7, 11), R(a, 4) and S(1, -3) be the vertices of a parallelogram PQRS, respectively.
Join PR and OS.
Let PR and QS intersect at a point T.

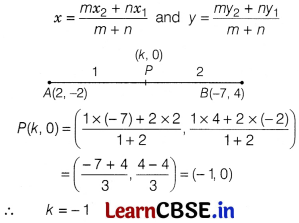
We know that the diagonals of a parallelogram bisect each other.
So, T is the mid-point of PR as well as that of QS.
∴ Mid-point of PR = Mid-point of QS
⇒ (\(\frac{1 + a}{2}\), \(\frac{4+4}{2}\)) = (\(\frac{7+1}{2}\), \(\frac{11-3}{2}\))
⇒ (\(\frac{1+a}{2}\), 4) = (4, 4)
On comparing the x-coordinate from both sides, we get
\(\frac{1+a}{2}\) = 4
⇒ 1 + a = 8 ⇒ a = 7
Hence, the value of a is 7.

DIRECTIONS: Two statements are given below – one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
(A) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A): If the height of the cone is 10 cm and the radius of the base is 7 cm, then the volume of the cone is 513.3 cm³.
Reason (R): According to assertion, if \(\sqrt{149}\) = 12.2, then curved surface area of a cone is 268.4 cm².
Solution:
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).

Explanation: For assertion:
Height (h) = 10 cm
and radius (r) = 7 cm

So, reason is also true.
Both A and R are true and R is not the correct
explanation of A.

Question 20.
Assertion (A): Mid-point of a line segment divides the line in the ratio 1:1.
Reason (R): If area of a triangle is zero that means points are collinear.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true but Reason (R) is false
(d) Assertion (A) is false but Reason (R) is true
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Both the Assertion (A) and Reason (R) are true but the Reason (R) is not the correct explanation of the Assertion (A).

Section – B (10 Marks)
Section B consists of 5 questions of 2 marks each.

Question 21.
Given that 3 is irrational, prove that 5 + 2√3 is irrational.
Solution:
Let us assume 5 + 2√3 is rational, then it must be in the form of \(\frac{p}{q}\) where p and q are co-prime integers and q ≠ 0
i.e.,  5 + 2√3 = \(\frac{p}{q}\)
So √3 = \(\frac{p-5 q}{2 q}\) … (i)
Since p, q, 5 and 2 are integers and q ≠ 0, RHS of equation (i) is rational. But LHS of (i) is √3 which is irrational. This is not possible.
This contradiction has arisen due to our wrong assumption that 5 + 2√3 is rational. So, 5 + 2√3 is irrational.

Question 22.
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80°, 40° at the centre are shown. Find the area (in cm2) of the shaded region. [2]

Solution:
Given, radius of circle, r = 7 cm
Now, area of shaded region = Area of three sectors

Question 23.

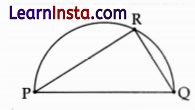
Shown below is a ΔPQR inscribed in a semicircle.
A circle is drawn such that QR is a tangent to it at the point R.
How many such circles can be drawn? Justify your answer.
Solution:
Infinite number of circles can be drawn.
Justification: ∠PRQ = 90° (Angle in semicircle)
Radius is perpendicular to the tangent at the point of contact.
∴ Infinite circles with radii lying on extended PR and R being a point on circumference of circle can be drawn.

Question 24.
In the given figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB = 125°, then find ∠APO. [2]

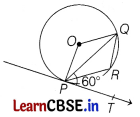
Solution:
∠OAP = 90°, AO ⊥ PA
Now, ∠AOP + ∠BOP = 180°
⇒ ∠AOP + 125° =180°
⇒ ∠AOP = 180° – 125° = 55°
Also, in ∆APO,
∠APO + ∠AOP + ∠PAO = 180°
⇒ ∠APO + 55° + 90° = 180°
⇒ ∠APO + 145° = 180°
∴ ∠APO = 180° – 145° = 35°

Question 25.

Jaya drew this rangoli design during a competition.
Circles C₁, C₂, C₃ and C₄ have common centre P.
The radius of circle C₁ is 6 cm.
The table given below shows the radii of circles in terms of the radius of circle C₁.

Radius of circle	Terms of the radius of C1
C2	2
C3	2.5
C4	3.5

(A) Jaya says,” Since the radius of circle C₄ is 3.5 times of the radius of circle C₁, the area occupied by circle C₄ is 3.5 times the area occupied by circle C₁.”
Is Jaya correct? Give reason.
Solution:
Here, radius of circle C₁ = 6 cm
Area of circle C₁ = πr₁²
= \(\frac{22}{7}\) × 6 × 6
= 113.14 cm
Also, radius of C₄ = 3.5 × radius of C₁
= 3.5 × 6 = 21 cm
∴ Area of circle C₄ = πr₄²
= \(\frac{22}{7}\) × 21 × 21
= 1386 cm²
No, Jaya is not correct as the area occupied by circle C₁ is 113.14 cm² whereas the area occupied by circle C₄ is 1386 cm² and 1386 is not 3.5 times 113.14.

OR

(B) If the area of a semi-circular field is 30800 sq.m, then find the perimeter of the field.
Solution:
Let the radius of the field be r.
We know that,
Area of semi-circle = \(\frac{1}{2}\)πr²
⇒ 30800 = \(\frac{1}{2}\)πr²
⇒ r² = 30800 × 2 × \(\frac{7}{22}\) [∵ π = \(\frac{22}{7}\)]
⇒ r² = 19600
⇒ r = 140 m [Taking positive square root]
How, perimeter of the field = πr + 2r
= \(\frac{22}{7}\) × 140 + 2 × 140
= 440 + 280
= 720 m

Section – C (18 Marks)
Section C Consists of 6 questions of 3 marks each

Question 26.
If the 3rd and 9th terms of an AP are 4 and – 8 respectively, then which term of this AP is zero?
Or
Find the common difference of an AP, whose first term is 1/2 and the 8th term is 17/6. Also, find the ratio of 4th term and 50th term. [3]
Solution:
Let a be the first term and d be the common difference of an AP.
∵ The nth term of an AP is a_n = a + (n – 1)d
∴ a₃ = a + 2d = 4 [∵ a₃ = 4, given]…(i)
and a₉ = a + 8d = -8 [∵ a₉ = -8, given]…(ii)
On subtracting Eq. (i) from Eq. (ii), we get
6d = -12
⇒ d = \(\frac{-12}{6}\) = -2
On putting the value of cf in Eq. (i), we get
a + 2 × (-2) = 4
⇒ a – 4 = 4
⇒ a = 4 + 4 = 8
Let the nth term of this AP be zero,
i.e. a_n = 0
⇒ a + (n – 1)d = 0
⇒ 8 + (n – 1) (-2) = 0
⇒ (n – 1)(-2) = -8
⇒ n – 1 = \(\frac{-8}{-2}\) = 4
∴ n = 4 + 1 = 5
Hence, 5th term of this AP is zero.

Or

Let a be the first term and d be the common difference of an AP.
Then, nth term, T_n = a + (n – 1) d
Given, 8th term,
T₈ = \(\frac{17}{6}\) ⇒ a + 7d = \(\frac{17}{6}\)
⇒ \(\frac{1}{2}\) + 7d = \(\frac{17}{6}\)
⇒ 7d = \(\frac{17}{6}\) – \(\frac{1}{2}\)
⇒ 7d = \(\frac{14}{6}\)
⇒ d = \(\frac{1}{3}\)

Now, 4th term, T₄ = a + 3d
= \(\frac{1}{2}\) +3(\(\frac{1}{3}\)) = \(\frac{1}{2}\) + 1 = \(\frac{3}{2}\)
and 50th term, 7₅₀ = a + 49d
= \(\frac{1}{2}\) + 49 × \(\frac{1}{3}\) = \(\frac{101}{3}\)
Required ratio = \(\frac{3/2}{101/6}\) = \(\frac{3}{2}\) × \(\frac{6}{101}\) = 9 : 101

Question 27.
The roots a and B of the quadratic equation x² – 5x + 3(k – 1) = 0 are such that α – β = 1. Find the value of k.
Solution:
We have,
α + β = 5 …(i)
α – β = 1 …(ii)
Solving (i) and (ii), we get
α = 3 and β = 2
also αβ = 5
or 3(k – 1) = 6
k – 1 = 2
k = 3

Question 28.
If a and 3 are zeroes of the polynomial x² – 2x – 15, then form a quadratic polynomial whose zeroes are 2α and 2ß.
Or
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers. [3]
Solution:
Let p(x) = x² – 2x -15
On comparing with ax² + bx + c, we get
a = 1, b = -2 and c = -15
Given, α and ß are the zeroes of p(x).
Sum of zeroes,
(α + β) = \(-\frac{b}{a}\)
⇒ α + β = \(-\frac{(-2)}{1}\)
⇒ α + β = 2 …………(i)
and product of zeroes, (αß) = \(\frac{c}{a}\)
⇒ αß = \(\frac{-15}{1}\)
⇒ αß = -15 …(ii)
We have to form a polynomial whose zeroes are 2α and 2β.
∴ Sum of zeroes = 2α + 2β = 2(a + β)
= 2 × 2 = 4 [usingEq. (i)]
and product of zeroes = 2α ⋅ 2 β
= 4 αβ
= 4 × (-15)
= – 60 [using Eq. (ii)]
∴ Required polynomial
= x² – (Sum of zeroes) x + (Product of zeroes)
= x² – 4x + (-60) = x² – 4x – 60

Or

Let the required numbers be x and y, where x > y.
Given, difference of squares of two numbers = 180
We have, x² – y² = 180 …(i)
and also it is given that the square of smaller number
= 8 × larger number
We have, y² = 8x …(ii)
From Eqs. (i) and (ii), we get
x² – 180 = 8x
⇒ x² – 8x – 180 = 0
⇒ x² – 18x + 10x – 180 = 0 [by factorisation]
⇒ x(x – 18) + 10(x – 18) = 0
⇒ (x – 18) (x + 10) = 0
⇒ x – 18 = 0 or x + 10 = 0
⇒ x = 18 or x = -10
Now, if x = 18, then square of smaller number
= 8 × 18 = 144 [from Eq. (ii)]
⇒ Smaller number = ± 12
⇒ Smaller number = 12 or -12
and if x = -10, then square of smaller number
= [8 × (-10)] = – 80, which is not possible as square of a number cannot be negative.
Hence, the required numbers are 18 and 12 or 18 and -12.

Question 29.
(A) ABDC is a quadrant of a circle of radius 28 cm and a semi-circle BEC is drawn with BC as diameter. Find the area of the shaded region. (use π = \(\frac{22}{7}\))

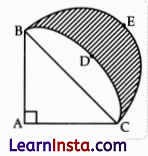
Solution:
As ABC is a quadrant of the drde, ∠BAC will be measured 90°.
In ΔABC, BC² = AC² + AB²
= (28)² + (28)²
= 2(28)²
∴ BC = 28√2 cm
Radius of semi-circle drawn on BC = \(\frac{28 \sqrt{2}}{2}\)
= 14 √2 cm
Area of semi-circle = \(\frac{1}{2}\) × \(\frac{22}{7}\) × (14√2)
= 616 cm²
Area of ΔABC = \(\frac{1}{2}\) × 28 × 28
= 392 cm²
Area of of quadrant = \(\frac{1}{2}\) × \(\frac{22}{7}\) × 28 × 28
= 616 cm²
Area of the shaded region = Area of semi-circle + Area of Δ – Area of quadrant
= 616 + 392 – 616
= 392 cm²

OR

(B) The area of a circular playground is 22176 cm². Find the cost of fencing this ground at the rate of ₹50 per metre.
Solution:
Area of a circular playground = 22176 cm²
i.e., πr² = 22176 cm²
[where r is the radius of the play ground]
⇒ r² = 22176 × \(\frac{7}{22}\) = 7056
⇒ r = 84 cm = 0.84 m
Cost of fencing this ground = ₹50 × 2πr
= ₹50 × 2 × \(\frac{22}{7}\) × 0.84
= ₹264

Question 30.
If(- 3, 2), (1, -2) and (5, 6) are the mid-point of the sides of a triangle, then find the coordinates of the vertices of the triangle. [3]
Solution:
Let A = (x₁, y₁), B = (x₂, y₂) and C = (x₃, y₃) be the coordinates of vertices of the triangle.
Let D (- 3, 2), E (1, -2) and F (5, 6) be the mid-points of the sides BC, CA and AB respectively.
Since, D(- 3,2) is the mid-point of BC
∴ \(\frac{x_2}{x_3}=-3\) and \(\frac{y_2}{y_1}=2\)

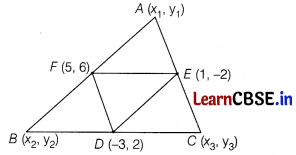
⇒ x₂ + x₃ = -6 ……..(i)
and y₂ + y₃ = 4 ……..(ii)
As, E(1, – 2) is the mid-point of AC
∴ \(\frac{x_1}{x_3}=1\) and \(\frac{y_1}{y_3}=-2\)
⇒ x₁ + x₂ = 2 …………(iii)
and y₁ + y₃ = -4 …………(iv)
Also, F(5, 6) is the mid-point of AB
∴ \(\frac{x_1}{x_2}=5\) and \(\frac{y_1}{y_2}=6\)
⇒ x₁ + x₂ = 10 ……….(v)
and y₁ + y₂ = 12 ……….(vi)
On adding Eqs. (i), (iii) and (v), we get
2(x₁ + x₂ + x₃) = 6
⇒ x₁ + x₂ + x₃ = 3 ……….(vii)
On subtracting Eqs. (i), (iii) and (v) from Eq. (vii) in turn, we get
x₁ = 9, x₂ = 1 and x₃ = -1
On adding Eqs. (ii), (iv) and (vi), we get
2(y₁ + y₂ + y₃) = -12
⇒ y₁ + y₂ + y₃ = -6 …(viii)
Subtracting Eqs. (ii), (iv) and (vi) from Eq. (viii) in turn, we get
y₁ = 2, y₂ = 10 and y₃ = – 6
Hence, the vertices of ∆ABC are A(9, 2), B(1, 10) and C(- 7, – 6).

Question 31.
The median of the following data is 16. Find the missing frequencies a and b, if the total of the frequencies is 70.

Solution:

Class	Frequency (f)	Cumulative frequency (c.f.)
0-5	12	12
5-10	a	12 + a
10-15	12	24 + a
15-20	15	39 + a
20-25	b	39 + a + b
25-30	6	45 + a + b
30-35	6	51 + a + b
35-40	4	55 + a + b
Total	70

According to question,
55 + a + 5 = 70
a + 5 = 15  … (i)

a = 8
Substituting the value of o in equation (i), we get
8 + b = 15
⇒ b = 15 – 8
⇒ b = 7

Section – D (20 Marks)
Section D consists of 4 questions of 5 marks each

Question 32.
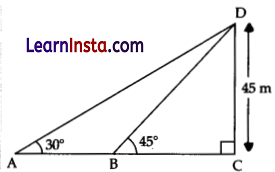
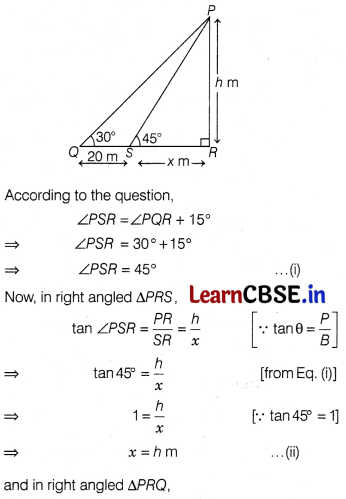
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 m towards the tower, the angle of elevation of the top increases by 15°, then find the height of the tower. [5]
Solution:
Let the height of the tower PR be h m, the angle of elevation at point 0 is 30° i.e. ∠PQR = 30° and S be the position of observer after moving 20 m towards the tower.

Question 33.

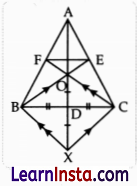
In ΔABC, AD is a median and O is any point on AD. BO and CO on producing meet AC and AB at E and F respectively. Now AD is produced to X such that OD = DX as shown in figure.
Prove that:
(i) EF || BC
(ii) AO : AX = AF : AB
Solution:
Since, BC and OX bisect each other.
So, BXCO is a parallelogram then BE || XC and BX || CF.

In ΔABX, by B.PT.,

or, OA : AX = AF : AB Hence Proved.

Question 34.
ABCD is a trapezium with AB || DC. E and F are two points on non-parallel sides AD and BC respectively, such that EF is parallel to AB. Show that \(\frac{A E}{E D}=\frac{B F}{F C}\) [5]

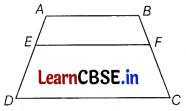
Solution:

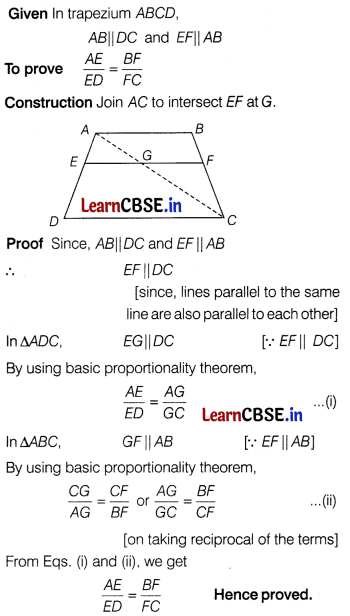
Question 35.
The first term of an A.P. is 3, the last term is 83 and the sum of all its terms is 903. Find the number of terms and the common difference of the A.P.
Solution:
Here a = 3, a_n = 83 and S_n = 903
Therefore 83 = 3 + (n – 1)d
⇒ (n – 1)d = 80 …(i)
Also 903 = \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{n}{2}\)[6 + 80]
= 43n [using (i)]

⇒ n = 21
and d = 4

Section – E (12 Marks)
Case study based questions are compulsory.

Question 36.
Traffic Light Signal
In our daily life we all see traffic lights. A traffic controller set the timmings of traffic lights in such a way that all light are not green at the same time or specially not in the rush hour. It may create problem in an hour because lights are for few minutes only. So, he take the timmings of nearby places in same area and calculate 1 cm of all traffic stops and he easily manage the traffic by increasing the duration or set at different times. There are two traffic lights on a particular highway which shows green light on time of 90 sec and 144 sec, respectively.

Based on above information, answer the following questions.
(i) Find the HCF of the time interval between two green lights. [2]
Or
Find the LCM of the time interval between two green lights.[2]
(ii) Factor tree is used for determining the ……. [1]
(iii) Identify whether the term HCF (a, b) × LCM (a, b) – ab is true or not. [1]
Solution:
(i) Using the factor tree for the prime factorisation of 90 and 144, we have
90 = 2 × 3² × 5and 144 = 2⁴ × 3²
To find the HCF, we list the common prime factors and their least exponents in 90 and 144 as under
Table
∴ HCF = 2¹ × 3² = 2 × 9 = 18

Or

To find the LCM, we list all prime factors of 90 and 144 and their greatest exponents as follows
Table
∴ LCM =24 × 32 × 51 =16 × 9 × 5 = 720
(ii) Factor tree is used for determining the prime factor.
(iii) The term is true,
HCF (a, b) × LCM (a, b) = ab
If a = 90, b = 144, then
LCM (a, b) = 720 and HCF (a, b) = 18
Now, LCM × HCF = 720 × 18 = 12960
and a × b = 90 × 144 = 12960
Thus, HCF (a, b) × LCM (a, b) = ab = 12960.

Question 37.
Read the following text and answer the questions given below:

A tiling or tessellation of a flat surface is the covering of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. Historically, tessellations were used in ancient Rome and in Islamic art. You may find tessellation patterns on floors, walls, paintings etc. Shown below is a tiled floor in the archaeological Museum of Seville, made using squares, triangles and hexagons.
A craftsman thought of making a floor pattern after being inspired by the above design. To ensure accuracy in his work, he made the pattern on the Cartesian plane. He used regular octagons, squares and triangles for his floor tessellation pattern.

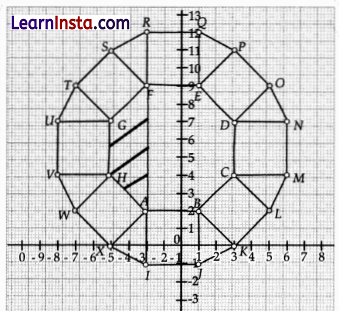
(i) What is the length of the line segment joining points B and F?
(ii) What are the co-ordinates of the point on y-axis equidistant from A and G?
Solition:
(i) B(1, 2), F(-2, 9)
BF2 = (-2 – 1)² + (9 – 2)²
= (-3)² + (7)²
= 9 + 49
= 58
So BF = √58 units

(ii) A(-2, 2), G(-4, 7)
Let the point on y-axis be Z(0, y)
AZ² = GZ²
(0 + 2)² + ( y – 2)² = ( 0 + 4)² + ( y – 7)²
(2)² + y² + 4 – 4y = (4)² + y² + 49 – 14y
8 – 4y = 65 – 14y
10y = 57
So, y = 5.7
i.e., The required point is (0, 5.7)

OR

What is the area of Trapezium AFGH?

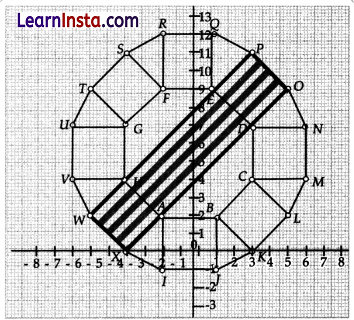
A(-2, 2), F(-2, 9), G(-4, 7), H(-4, 4)
Clearly GH = 7 – 4 = 3units
AF = 9 – 2 = 7 units
∴ So, height of the trapezium AFGH = 2 units
So, area of AFGH = \(\frac{1}{2}\)(AF + GH) × height
= \(\frac{1}{2}\)(7 + 3) × 2
= 10 sq. units

(iii) The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the co-ordinates of Z?
Solution:

W(~6, 2), X(-4, 0), O(5, 9), P(3, 11)
Clearly WXOP is a rectangle.
Point of intersection of diagonals of a rectangle is the mid point of the diagonals. So the required point is mid point of WO or XP.
= \(\left(\frac{-6+5}{2}, \frac{2+9}{2}\right)\)
= \(\left(\frac{-1}{2}, \frac{11}{2}\right)\)

Question 38.
Based on above information answer the following questions.
(i) Find the probability of getting a king of red colour. [1]
(ii) Find the probability of getting a face card. [1]
(iii) Find the probability of getting a jack of hearts. [2]
Or
Find the probability of getting a spade. [2]
Solution:
Total number of cards in one deck of cards is 52.
∴ Total number of outcomes =52
(i) Let E₁ = Event of getting a king of red colour
∴ Number of outcomes favourable to £-, = 2
[∴ there are four kings in a deck of playing cards out of which two are red and two are black]
Hence, the probability of getting a king of red colour.
P(E₁) = \(\frac{2}{52}\) = \(\frac{1}{26}\)

(ii) Let E₂ = Event of getting a face card
∴ Number of outcomes favourable to E₂ = 12
[∴ in a deck of cards, there are 12 face cards, namely 4 kings, 4 jacks, 4 queens]
Hence, the probability of getting a face card,
P(E₂) = \(\frac{12}{52}\) = \(\frac{3}{13}\)

(iii) Let E₃= Event of getting a jack of heart
∴ Number of outcomes favourable to E₃ = 1
[∵ there are four jack cards in a deck, namely 1 of heart, 1 of club, 1 of spade and 1 of diamond]
Hence, the probability of getting a jack of heart,
P(E₃) = \(\frac{1}{52}\)
Or
Let E₄ = Event of getting a spade
∴ Number of outcomes fourable to E₄ = 13
[∵ in a deck of cards, there are 13 spades, 13 clubs, 13 hearts and 13 diamonds]
Hence, the probability of getting a spade,
P(E₄) = \(\frac{13}{52}\) = \(\frac{1}{4}\)

Must Read:

SBIN Pivot Point Calculator