CBSE Sample Papers for Class 10 Maths Standard Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Set 2 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 MCQs carrying 1 mark each
3. Section B has 5 questions carrying 02 marks each.
4. Section C has 6 questions carrying 03 marks each.
5. Section D has 4 questions carrying 05 marks each.
6. Section E has 3 case based integrated units of assessment (04 marks each) with sub parts of the values of 1, 1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2. Qs of 5 marks, 2.Qs of 3 marks and 2. Questions of 2. marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take n =22/7 wherever required if not stated.

Section – A ( 20 Marks) 
Section A Consists of Multiple Choice Type questions of 1 mark each

Question 1.
Let p be a prime number and k be a positive integer
If p divides k², then which of these is DEFINITELY divisible by p?

\(\frac{k}{2}\)

k

7k

k3

(A) Only k
(B) Only k and 7k
(C) Only k, 7kand 7k³
(D) all \(\frac{k}{2}\), k, 7k and k³
Solution:
(C) Only k, 7kand 7k³

Explanation: k² is divisible by p
∴ k will be divisible by p.
From the given condition we can check the divisibility by k.
\(\frac{k}{2}\)√k = \(\frac{1}{2}\)
k + k = 1
7k + k = 7
k³ + k = k²
From above we can see that the conditions (ii), (iii) and (iv) are completely divisible by k, so these will also be divisible by p but the condition (i) is not completely divisible by k, so it will also not be divisible by p.

Question 2.
The distance between the points A(a + b, a – b) and B(a – b, – a – b) is
(a) 2\(\sqrt{b^2+a^2}\)
(b) \(\sqrt{b^2+a^2}\)
(c) 2\(\sqrt{b^2-a^2}\)
(d) \(\sqrt{b^2-a^2}\)
Answer:
(a) 2\(\sqrt{b^2+a^2}\)

The distance between the points A(a + b, a – b) and B(a – b, -a – b) is

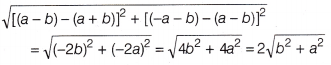
Question 3.
Which of these is a QUADRATIC equation having one of its roots as zero?
(i) x³ + x² = 0
(ii) x² – 2x = 0
(iii) x² – 9 = 0
(A) only (i)
(B) only (ii)
(C) only (i) and (ii)
(D) only (ii) and (iii)
Solution:
(B) only (ii)

Explanation: (i) x³ + x² = 0
It is cubic so it is not possible.
(ii) x² – 2x = 0
⇒ x(x – 2) = 0
⇒ x = 0 and x = 2
Thus, it has one of its roots as zero.
(iii) x² – 9 = 0
⇒ (x + 3)(x – 3) =0
⇒ x + 3 = 0 and x – 3 = 0
x = -3 and x = 3
It does not have any of its roots as zero.
Thus only (ii) has one of its roots as zero.

Question 4.
If sin(A -B) = sin A cos B – cos Asin B, then the value of sin 15° is
(a) \(\frac{\sqrt{3}-1}{\sqrt{2}}\)
(b) \(\frac{\sqrt{2}-1}{2 \sqrt{2}}\)
(c) \(\frac{1-\sqrt{3}}{2 \sqrt{2}}\)
(d) \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
Answer:
(d) \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

We have, sin(A – B) = sinAcosB – cosAsinB
Put A = 45° and B = 30°, we get
sin(45° – 30°) = sin45°cos30° – cos45°sin30°
= \(\frac{1}{\sqrt{2}}\) × \(\frac{\sqrt{3}}{2}\) – \(\frac{1}{\sqrt{2}}\) × \(\frac{1}{2}\)
\(=\frac{\sqrt{3}}{2 \sqrt{2}}\) – \(\frac{1}{2 \sqrt{2}}\) = \(\frac{1}{2 \sqrt{2}}\)

Question 5.

The cylindrical bumps on top of lego blocks are called studs. Pragun has built a solid inverted lego pyramid as shown below. The number of studs in successive floors forms an arithmetic progession. Pragun figures out that the sum of the number of studs used in the first p floors is given by (6p² – 2p). The number of studs are:
(Note: The figure is only visual representation.)
(A) 140
(B) 88
(C) 64
(D) 52
Solution:
(D) 52

Explanation:
S_p = 6p² – 2p
S₁ = 6 × 1² – 2 × 1
= 6 – 2
= 4
S₂ = 6 × 2² – 2 × 2
= 24 – 4
= 20
Now, S₂ = T₂ + T₁
20 = T₂ + 4 (AS, S₁ = T₁)
T₂ = 16
Common difference (d) = T₂ – T₁
= 16 – 4 = 12
Thus, a = 4, d = 12 and n = 5
∴ T_n = a + (n – 1)d
= 4 + (5 – 1)12
= 4 + 48 = 52

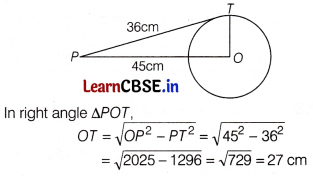
Question 6.
A point P is 45 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 36 cm. The radius of the circle is
(a) 27 cm
(b) 17 cm
(c) 37 cm
(d) 12 cm
Answer:
(a) 27 cm

We know that the radius drawn from centre O to the tangent line is perpendicular.

Question 7.
X-axis divides the join of (2, -3) and (5, 6) in the ratio:
(A) 1:2
(B) 2:1
(C) 2:5
(D) 5:2
Solution:
(A) 1:2

Explanation: Let P(x, 0) be a point on X-axis which divides the join of A(2, – 3) and B(5, 6) in the ratio m : n, then using section formula

⇒ 6m – 3n = 0
⇒ 2m – n = 0
⇒ 2m = n
\(\frac{m}{n}\) = \(\frac{1}{2}\)
i.e., m : n = 1 : 2

Question 8.
The 10th term from the end of the AP sequence 4, 9, 14, ……., 254 is
(a) 208
(b) 210
(c) 209
(d) None of these
Answer:
(c) 209

Given, the AP sequence is 4, 9, 14, ………, 254.
Here, a = 4, d = 9 – 4 = 5 and l = 254
∴ 1oth term from the end = l – (10 – 1)d
= 254 – (9) × 5
= 254 – 45 = 209

Question 9.

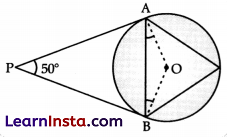
In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to:
(A) 25°
(B) 30°
(C) 40°
(D) 50°
Solution:
(A) 25°

Explanation: In ΔOAB, we have
OA = OB (Radii of same circle)
∴ ∠OAB = ∠OBA(Angles opposite to equal sides are equal)
As OA and PA are radius and tangent respectively at point of contact A.
So, ∠OAP = 90°
Similarly, ∠OBP = 90°
Now, in quadrilateral PAOB,
∠P + ∠A + ∠O + ∠B = 360°
⇒ 50° + 90° + ∠O + 90° = 360°
⇒ ∠O = 360° – 90° – 90° – 50°
⇒ ∠O = 130°
Again, in ΔOAB,
∠O + ∠OAB + ∠OBA = 180°
⇒ 130° + ∠OAB + ∠OAB = 180° (∵ ∠OBA = ∠OAB)
⇒ 2∠OAB = 180° – 130° = 50°
⇒ ∠OAB = 25°

Question 10.
The zeroes of the polynomial f(x) = 4x² + 8x are
(a) 2, 0
(b) -2, 2
(c) 0, 1
(d) 0, -2
Answer:
(d) 0, -2

Given, f(x) = 4x² + 8x
The zeroes of f(x) are given by f(x) = 0
∴ 4x² + 8x = 0 ⇒ x(4x + 8) = 0
⇒ x = 0 or 4x + 8 = 0 ⇒ x = 0 or x = -2
Hence, zeroes of f(x) are 0 and -2,

Question 11.
P and Q are acute angles such that P > Q.
Which of the following is DEFINITELY true?
(A) sin P < sin Q
(B) tan P > tan Q
(C) cos P > cos Q
(D) cos P > sin Q
Solution:
(B) tan P > tan Q

Explanation: P > Q (given)
Let P = 60° and Q = 0°
(i) sin P < sin Q = False   (As, sin P > sin Q)
(ii) tan P > tan Q = True
(iii) cos P > cos Q = false  (As, cos P < cos Q)
(iv) cos P > sin Q = false  (As cos P < sin Q)

Question 12.
The coordinate of the point, in which the diagonals of the parallelogram formed by joining the points (-2, -1), (1,0), (4, 3) and (1, 2) intersect are
(a) (0, 1)
(b) (1, 1)
(c) (1, 2)
(d) None of these
Answer:
(b) (1, 1)

Given, vertices of a parallelogram are A(-2, -1) B(1, 0), C(4, 3) and D(1, 2).
We know that diagonals of a parallelogram intersect at mid-point.
∴ The coordinate of the intersection point of the diagonal = mid-point of AC
= \(\left(\frac{-2+4}{2}, \frac{-1+3}{2}\right)\) = \(\left(\frac{2}{2}, \frac{2}{2}\right)\) = (1, 1)

Question 13.
If the height of a vertical pole is √3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is:
(A) 30°
(B) 60°
(C) 45°
(D) 75°
Solution:
(B) 60°

Explanation: Let the length of shadow is x,

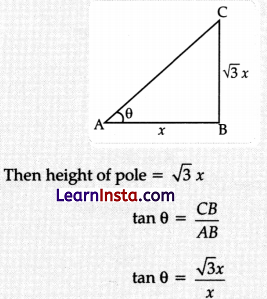
tan θ = √3
tan θ = tan 60°
θ = 60°

Question 14.
The probability that a number selected from the numbers 1, 2, 3, …, 15 is a multiple of 4 is
(a) 0
(b) 1
(c) \(\frac{1}{10}\)
(d) \(\frac{1}{5}\)
Answer:
(d) \(\frac{1}{5}\)

The possible outcomes = 15
The number of favourable multiple of 4 = {4, 8, 12}
∴ P(getting a multiple of 4) = \(\frac{3}{15}\) = \(\frac{1}{5}\)

Question 15.
The sum of the circumference and the radius of a circle is 102 cm. The radius of the circle is:
(A) 7 cm
(B) 14 cm
(C) 10 cm
(D) 18 cm
Solution:
(B) 14 cm

Explanation: Let radius of circle be r.
∴ Circumference of circle = 2πr
According to question,
2πr + r = 102
or, r (2 × \(\frac{22}{7}\) + 1) = 102
or, r = \(\frac{102 × 7}{51}\)
= 14 cm

Question 16.
The quadratic equation 9x² + 6kx + 4 = 0 has equal roots. Then, the value of k is
(a) 2, -2
(b) 2, 2
(c) 0, 2
(d) – 2, 0
Answer:
(a) 2, -2

Given, quadratic equation is 9x² + 6kx + 4 = 0.
On comparing with ax2 + bx + c = 0, we get
a = 9, b = 6k and c = 4
The condition for quadratic equation has equal roots i.e. b² – 4ac = 0
i.e., b² – 4ac = 0
∴ (6k)² – 4 × 9 × 4 = 0
⇒ 36k² – 144 = 0
⇒ k² = \(\frac{144}{36}\)
⇒ k² = 4
⇒ k = ±2 [taking square roots]

Question 17.
At a party, there is one last pizza slice and two people (Ananya and Pranit) who want it. To decide who gets the last slice, two fair six-sided dice are rolled, if the largest number in the roll is: 1,3 or 6, Ananya would get the last slice, and 2, 4 or 5, Pranit would get it.
In a random roll of dice, who has a higher chance of getting the last pizza slice?
(Note: If the number on both the dice is the same, then consider that number as the larger number)
(A) Ananya
(B) Pranit
(C) Both have an equal chance
(D) (cannot be answered without knowing the exact number in a roll)
Solution:
(B) Pranit

Explanation: Total outcomes = 6 × 6 = 36
Favourable outcomes for Ananya = (1, 2), (2, 1), (1, 5), (2, 4), (3, 3), (4, 2), (5, 1) = 7 outcomes
∴ P(Ananya getting last slice) = \(\frac{7}{36}\)  …(i)
Favourable outcome for Pranit = (1,1), (1, 3), (2, 2) (3, 1), (1, 4), (2, 3), (3, 2), (4, 1) = 8 outcomes
∴ P(Pranit getting last slice) = \(\frac{8}{36}\)  …(ii)
From (i) and (ii)
Pranit has a higher chance of getting the last Pizza slice.

Question 18.
A pair of dice is thrown once, then the probability of getting an even doublet is
(a) 0
(b) 1
(c) \(\frac{1}{12}\)
(d) None of these
Answer:
(c) \(\frac{1}{12}\)

When two dice are thrown, then the possible number of outcomes = 6 × 6 = 36
The number of favorable even doublets = {(2, 2), (4, 4), (6, 6)}
∴ P(getting a doublet) = \(\frac{3}{36}\) = \(\frac{1}{12}\)

DIRECTIONS: Two statements are given below – one labelled Assertion (A) and the other labelled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
(A) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).
(C) (A)is true but (R) is false.
(D) (A) is false but (R) is true.

Question 19.
Assertion (A): The volume of a right circular cylinder of base radius 7 cm and height 10 cm is 1540 cm.
Reason (R): According to the assertion, the curved surface area of cylinder is 440 cm².
Solution:
(A) Both (A) and (R) are true and (R) is the correct explanation of the (A).

Explanation; In case of assertion:
Here r = 7 cm, h = 10 cm,
Volume of cylinder = πr²h
= \(\frac{22}{7}\) × (7)² × 10
= 1540 cm³
∴ Assertion is true.
In case of reason:
Curved Surface area of cylinder = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 10
= 440 cm²
∴ Reason is true.
Both A and R are true and Ris the correct explanation of A.

Question 20.
Assertion (A) If in an ∆ABC, a line DE || BC, intersects AB at D and AC at E, then \(\frac{A B}{A D}\) = \(\frac{A C}{A E}\)
Reason (R) If a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

The reason is true,

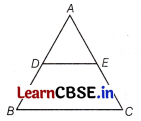
For Assertion (A),
Since, DE || BC
∴ By Thales Theorem

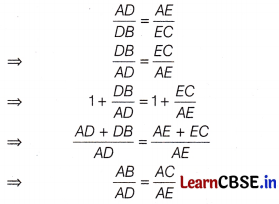
∴ Both Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).

Section – B (10 Marks)
Section B consists of 5 questions of 2 marks each.

Question 21.
Show that 5+2√7 is an irrational number, where √7 is given to be an A irrational number.
Solution:
Let, 5 + 2√7 be rational.
So 5 + 2√7 = \(\frac{p}{q}\),
where′a′and′b′are integers and q ≠ 0
2√7 = \(\frac{p}{q}\) – 5
√7 = \(\frac{p-5q}{2q}\)
Since ‘a’ and ‘b’ are integers p – 5q is also an integer \(\frac{p-5q}{2q}\) is rational. So RHS is rational.
LHS should be rational. but it is given that √7 is irrational.
Our assumption is wrong.
So 5 + 2√7 is an irrational number.

Question 22.
Without solving the following quadratic equation, find the value of m for which the given equation has real and equal roots.
x² + 2 (m -1 )x + (m + 5) = 0
Answer:
Given, quadratic equation is
x² + 2 (m – 1)x + (m + 5) = 0
On comparing it with ax² + bx + c = 0, we get
a = 1, b = 2(m – 1) and c = m + 5
Since the given equation has real and equal roots.
So, the discriminant will be zero
i.e. b² – 4ac = 0
⇒ [2(m – 1)]² – 4 × 1 × (m + 5) = 0
⇒ 4(m – 1)² – 4(m + 5) = 0
⇒ 4[m² + 1² – 2m – m – 5] = 0
[∵ (a – b)² = a² + b² – 2ab]
⇒ m² – 3m – 4 = 0 [dividing by 4]
⇒ m² – 4m + m – 4 = 0
[splitting the middle term]
⇒ m(m – 4) + 1(m – 4) = 0
⇒ (m + 1)(m -4) = 0
⇒ m + 1 = 0 or m – 4 = 0
m = -1 or m = 4
Hence, the values of m are -1 and 4.

Question 23.

In the figure below, a circle with centre O is inscribed inside ALMN. A and B are the points of tangency.
(Note: The figure is not to scale.)
Find ∠ANB. Show your steps.
Solution:
Reflex ∠AOB + minor ∠AOB = 360° (Complete Angle)
So, minor ∠AOB = 360° – 260°
= 100°
OA ⊥ LN (point of tangency)
Similarly, OB ⊥ NM
∴ ∠OAN = 90°
and ∠OBN = 90°
Now, in quadrilateral NAOB
∠NAO +  ∠AOB +  ∠OBN + ∠BNA = 360°
90° + 100° + 90° + ∠BNA = 360°
∠ANB = 360° – 280°
= 80°
Hence, ∠ANB = 80°

Question 24.
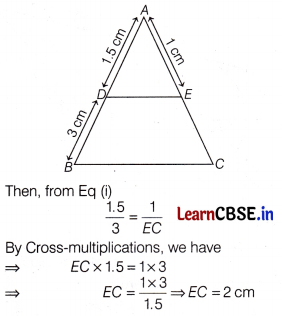
In the given figure DE || BC find EC.
Also given AD = 1.5 cm, DB = 3 cm and AE = 1 cm.

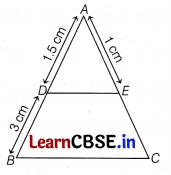
Answer:
Since, DE || BC [given]
∴ Using the Basic Proportionality theorem.
We have, \(\frac{A D}{D B}\) = \(\frac{A E}{E C}\)
Since, AD = 1.5 DB = 3 cm and AE = 1 cm

Question 25.

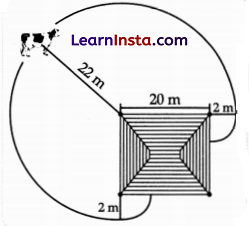
(A) A cow is tied at one of the corners of a square shed. The length of the rope is 22 m.
The cow can only eat the grass outside the shed as shown below.
What is the area that the cow can graze on? Show your steps.
Solution:
Total area cow can grazed = (3 quarters sector with radius 22 m) + (2 quarters sector with radius 2 m)
∴ Total area = \(\left[\frac{3}{4} \pi \times(22)^2+2 \times \frac{1}{4} \pi \times 4\right]\)
= \(\left(\frac{3}{4} \pi \times 484+\frac{1}{2} \pi \times 4\right)\)
= 363π + 27π
= 3657π m²

OR

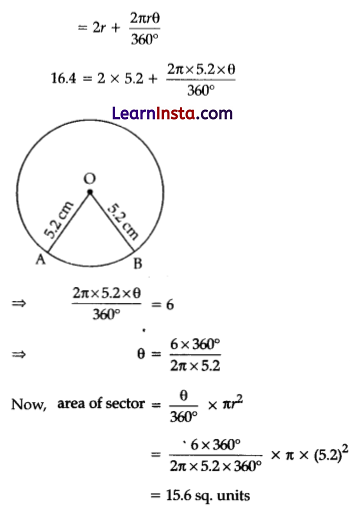
(B) The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
Solution:
Given, radius of circle (r) = 5.2 cm
i.e., OA = OB = r = 5.2 cm
and the perimeter of a sector = 16.4 cm
As we know the perimeter of the sector

Section – C (18 Marks)
Section C Consists of 6 questions of 3 marks each

Question 26.
Find a relation between x and y, such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).

Or

Find the ratio in which the point (-3, p) divides the line segment joining the points (-5, -4) and (-2, 3). Also, determine the value of p.
Answer:
Let the point A(x, y) be equidistant from the points B(3, 6) and C(-3, 4).

Or

Suppose the point P(-3, p) divides the line segment joining the points A(-5, -4)and B(-2, 3) in the ratio k : 1.
Then, the coordinates of P are \(\left(\frac{-2 k-5}{k+1}, \frac{3 k-4}{k+1}\right)\)
But, the coordinates of P are given as (-3, p).
∴ \(\frac{-2 k-5}{k+1}\) = -3 and \(\frac{3 k-4}{k+1}\) = p
⇒ -2k – 5 = -3k – 3
⇒ k = 2
Hence, point P divides the line segment joining points A and B in the ratio 2 : 1.
Now, consider p = \(\frac{3 k-4}{k+1}\)
p = \(\frac{3 \times 2-4}{2+1}\)
= \(\frac{6-4}{3}\) = \(\frac{2}{3}\)

Question 27.

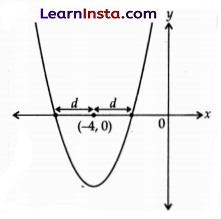
Shown below is the graph of a quadratic equation y = (x² + kx + 12).
Without finding the value of k, find the two roots of the given quadratic equation.
Show your steps.
Solution:
Let the point of intersection at x-axis be α and β
∴ α = (-4 + d) and β = (-4 – d)
Now, in quadratic equation y = (x² + kx + 12).
αβ = \(\frac{c}{a}\) = 12
∴ (-4 + d)(-4 – d) = 12
16 + 4d – 4d – d² = 12
– d² = 12 – 16
d² = 4
d = 2 and -2
By substituting value of d in α and p,
We can get roots of the given equation
α = -4 + 2 = -2
P = -4 – 2 = -6

Question 28.
Prove that 7 – 2\(\sqrt{5}\) is irrational.
Answer:
Let us assume to the contrary that 7 – 2\(\sqrt{5}\) is a rational number.
Then, it can be expressed in the form \(\frac{a}{b}\), where a and b are coprime integers and b ≠ 0.
Now, 7 – 2\(\sqrt{5}\) = \(\frac{a}{b}\), where a and b are integers and b ≠ 0.
⇒ 2\(\sqrt{5}\) = 7 – \(\frac{a}{b}\) ⇒ \(\sqrt{5}\) = \(\frac{7}{2}\) – \(\frac{a}{2b}\)
Since a and b are integers b ≠ 0, therefore \(\frac{a}{2b}\) is rational number and so \(\frac{7}{2}\) – \(\frac{a}{2b}\) is a rational number as difference of two rational number is also a rational number,
⇒ \(\sqrt{5}\) is a rational number.
But this contradicts the fact that \(\sqrt{5}\) is an irrational number.
This shows that our assumption is incorrect.
So, 7 – 2\(\sqrt{5}\) is irrational. Hence proved.

Question 29.
(A) Shown below is a circle whose centre is unknown.

State true or false for the statements below and give valid reasons.
(i) The centre of the circle can be found using any 2 tangents.
(ii) The centre of the circle can be found using any 2 chords.
Solution:
(i) True
Explanation: If we draw 90° angles at the point of contact of the two tangents and extend perpendicular lines to meet at a point they will give the centre of the circle.
(ii) True
Explanation: Drawing the perpendicular bisectors of the two chords and extending them to meet at a point gives the centre of the circle.

(B) ABCD is a square. CD is a tangent to the circle with centre O as shown in the figure below.

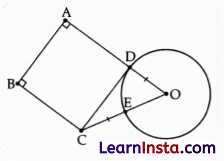
(Note: The figure is not to scale.)
If OD = CE, what is the ratio of the area of the circle and the area of the square? Show your steps and give valid reasons.
Solution:
OD = OE (equal radii) …(i)
And, OD = CE (Given) …(ii)
OC = OE + EC
= OD + OD
(From (i) and (ii))
∴ OC = 2OD …(iii)
CD is tangent (Given)
∴ OD ⊥ CD
Now, In right ΔODC
OC² = OD² + CD²
(2OD)² = OD² + CD² (∴ OC = OD)
4OD² – OD² = CD²
3OD² = CD² …(iv)
Now, Area of circle = πr² = π × OD²
Area of square = (side)² = (CD)²
= 3OD2  (From (iv))
\(\frac{Area of Circle}{Area of Square}\) = \(\frac{\pi \mathrm{OD}^2}{3 \mathrm{OD}^2}\) = \(\frac{\pi}{3}\)
Hence, ratio of the area of circle and area of the square = π : 3

Question 30.
From an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
Answer:
Given P is an external point and two tangents PA and PB are drawn.
To prove OP is the perpendicular bisector of AB.

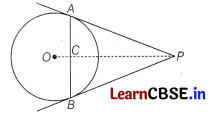
Proof Suppose OP intersects AB at C. In triangles ∆PAC and ∆PBC, we have PA = PB
[tangents drawn from an external point are equal]
∠APC = ∠BPC
[tangents PA and PB are equally inclined to OP]
and PC = PC [common side]
∴ ∆PAC\(\cong\) ∆PBC [by SAS congruency criterion]
⇒ AC = BC
and ∠ACP = ∠BCP [byCPCT]
But ∠ACP + ∠BCP = 180°
⇒ ∠ACP = ∠BCP = 90°
Hence, OP ⊥ AB
Hence proved.

Question 31.
The frequency distribution of daily rainfall in a town during a certain period is shown below.

Rainfall (in mm)	Number of days
0-20	7
20-40	x
40-60	10
60-80	4

Unfortunately, due to manual errors, the information on the 20-40 mm range got deleted from the data.
If the mean daily rainfall for the period was 35 mm, find the number of days when the rainfall ranged between 20-40 mm. Show your work.
Solution:

Rainfall (mm)	Number of days Frequency (fi)	Class- mark (xi)	(fixi)
0-20	7	10	70
20-40	x	30	30x
40-60	10	50	500
60-80	4	70	280
Total	21 + x		850 + 30x

Mean = 35 mm (Given)
And, Mean = \(\frac{850+30 x}{21+x}\)
35 = \(\frac{850+30 x}{21+x}\)
735 + 35x = 850 + 30x
5x = 115
x = 23
Hence, number of days are 23.

Section – D (20 Marks)
Section D consists of 4 questions of 5 marks each

Question 32.
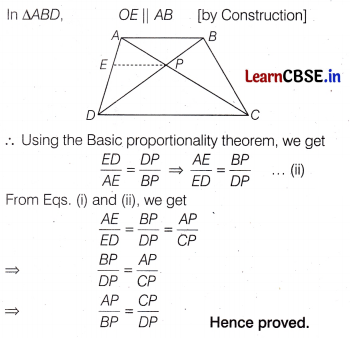
ABCD is a trapezium in which AB||DC and its diagonal intersect each other at the point P. Show that \(\frac{A P}{B P}\) = \(\frac{C P}{D P}\).
Answer:
We have a trapezium ABCD such that AB || DC. The diagonals AC and BD intersect each other at P.
Let us draw PE parallel to either AB or DC.
In ∆ADC PE || DC [by Construction]
∴ Using the Basic proportionality theorem, we get
\(\frac{A E}{E D}\) = \(\frac{A P}{C P}\)

Question 33.

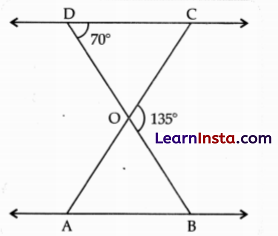
In the given figure, ΔODC ~ ΔOBA, ∠BOC = 135° and ∠CDO = 70°
find the angles ∠DOC, ∠DCO and ∠OAB.
(Note: The figure is not scale.)
Solution:
From the figure given in question, it is clear the DOB is a straight line
∴ ∠DOC + ∠COB = 180° [by linear pair axiom]
⇒ ∠DOC + 135 = 180°
⇒ ∠DOC = 180° – 135° = 45°
In ΔDOC,
∠DCO + ∠CDO + ∠DOC = 180° [by angle sum property of a triangle]
⇒ ∠DCO + 70° + 45° = 180°
⇒ ∠DCO = 180° – 115° = 65° [∴ ∠CDO = 70° and ∠DOC = 45°]
Given, ΔODC ~ ΔOBA
⇒ ΔOAB = ∠OCD = ∠DCO
∠OAB = 65°
Here, ∠DOC = 45°, ∠DCO = 65° and ∠OAB = 65°

Question 34.
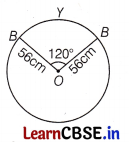
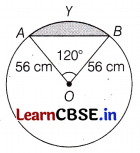
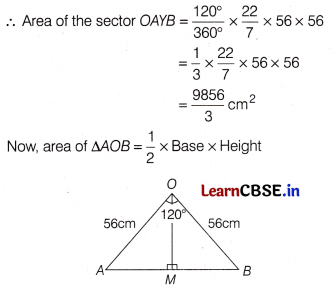
Find the area of sector OAYB and area of triangle AOB shown in figure, if radius of the circle is 56 cm and ∠AOB = 120°.
[Take, π = \(\frac{22}{7}\)]

Answer:
Given, r = 56cm and ∠AOB =120°




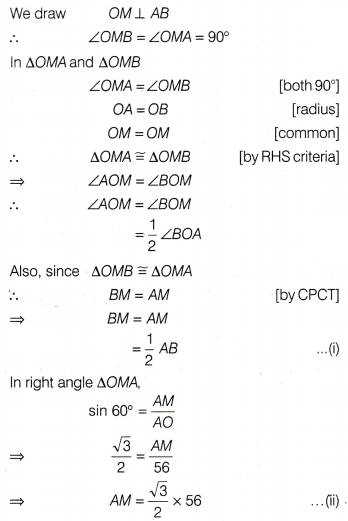
From Eq. (i),
AM = \(\frac{1}{2}\)AB
⇒ 2AM = AB
⇒ AB = 2AM ……….(iii)
From Eqs. (ii) and (iii), we get
AB = 2 × \(\frac{\sqrt{3}}{2}\) × 56
⇒ AB = 56\(\sqrt{3}\)
Now, area (∆MOB) = \(\frac{1}{2}\) × AB × OM
= \(\frac{1}{2}\) × 56\(\sqrt{3}\) × \(\frac{56}{2}\)
= 784\(\sqrt{3}\) cm².

Question 35.
If the median of the following frequency distribution is 32.5. Find the values of f1 and f2.

Solution:

Class	Frequency (f)	Cumulative Frequency (c.f.)
0-10	f1	f1
10-20	5	f1 + 5
20-30	9	f1 + 14
30-40	12	f1 + 26
40-50	f2	f1 + f2 + 26
50-60	3	f1 + f2 + 29
60-70	2	f1 + f2 + 31
	N = ∑f = 40

Now f₁ + f₂ + 31 = 40
f₁ + f₂ = 9
f₂ = 9 – f₁
Given that median is 32.5, which lies in 30 – 40
Hence, median class = 30 – 40.
Here; l = 30, \(\frac{N}{2}\) = \(\frac{40}{2}\) = 20, f = 12 and c.f. = 14 + f₁
Now, median = 32.5

⇒ 60 – 10f₁ = 30
⇒ 10f₁ = 30
⇒ f₁ = 3
From eq (i), we get f₂ = 9 – 3 = 6
Hence, f₁ = 3 and f₂ = 6

Section – E (12 Marks)
Case study based questions are compulsory.

Question 36.
Applications of Parabolas-Highway Overpasses/Underpasses

A highway underpass is parabolic in shape.

A parabola is the graph that result from p(x) = ax² + bx + c. Parabolas are symmetric about a vertical line known as the Axis of Symmetry.

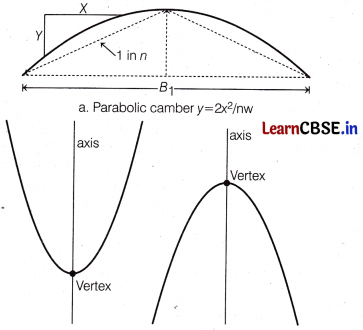
The axis of symmetry runs through the maximum or minimum point of the parabola which is called the vertex.

Based on the above information, answer the following questions.
(i) If the highway overpass is represented by x² – 2x – 8. Then, find its zeroes. (2)

Or

What is the representation of a Highway Underpass whose one zero is 6 and the sum of the zeroes is 0? (2)
(ii) Graph of a quadratic polynomial is a ……….. (1)
(iii) Find the number of zeroes of the polynomial f(x) = (x – 2)² +2. (1)
Answer:
(i) Let p(x) = x² – 2x – 8
= x² – (4 – 2)x – 8
[splitting middle term]
= x² – 4x + 2x – 8
= x(x – 4) + 2(x – 4)
= (x + 2)(x – 4)
To find the zeroes, put p(x) = 0
⇒ (x + 2)(x – 4) = 0
⇒ x + 2 = 0 or x – 4 = 0
⇒ x = -2 or x = 4

Or

Given, one of the zeroes of a polynomial is α = 6
and sum of zeroes, α + β = 0
⇒ 6 + β = 0
⇒ β = -6
Now product of zeroes,
αβ = 6 × (-6) = -36
Now, polynomial is
x² – (sum of zeroes)x + product of zeroes
∴ x² – (0)x + (-36) or x² – 36
Hence, the representation of highway underpass is x² – 36.

(ii) The graph of a quadratic polynomial is the shape of parabola.

(iii) We have, f(x) = (x – 2)² + 2
⇒ f(x) = x² + 4 – 4x + 2
⇒ f(x) = x² – 4x + 6
On comparing ax² + bx + c = 0, we get
a =1, b = -4 and c = 6
Now, b² – 4ac = (-4)² – 4 × 1 × 6
= 16 – 24
= -8 < 0
Hence, number of zeroes of given polynomial is zero.

Question 37.
Read the following text and answer the questions that follows:
Ronit is the captain of his school football team. He has decided to use a 4-4-2-1 formation in the next match. The figure below shows the positions of the players in a 4-4-2-1 formation on a coordinate grid.

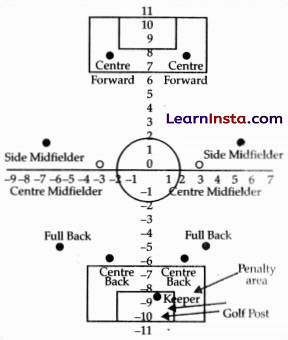
(i) What is the distance between the two centre forward positions in Ronit’s plan?
Solution:
Since centre forward belongs to 1st and find quadrants whose coordinatesare (3, 8) and (-3, 8) therefore the distance between of them.

(ii) Mention two positions which are not equidistant from any axis.
Solution:
From the given graph,
The distance between side midfielder (7, 2) and full back (5, -5)

So, both distances are not equal. Hence, the positions of side midfielder and full back are not equidistant from any axis, similarly the positions of side midfielder and centre midfielder are not equidistant from any axis.

OR

A ball hit from the left full back position travels uninterrupted to the right centre forward position. What can be the minimum distance travelled by the ball?
Solution:
Position of the left full back = (-6, -5) and the position of the right centre forward = (3, 8)
Distance between the position of left full back and right centre forward

(iii) Find the position of the goal keepar in the above graph.
Solution:
The position of the goal keeper is (0, -9).

Question 38.
A satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka, them being Nanda Devi (height 7,816 m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite to the top of Nanda Devi and Mullayanagiri are 30° and 60° respectively. If the distance between the peaks of two mountains is 1937 km and the satellite is vertically above the midpoint of the distance between the two mountains.

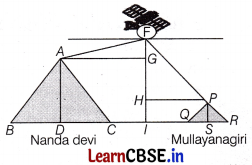
(i) Find the distance of the satellite from the top of Nanda Devi.
(ii) Find the distance of the satellite from the top of Mullayanagiri.
(iii) Find the distance of the satellite from the ground.

Or

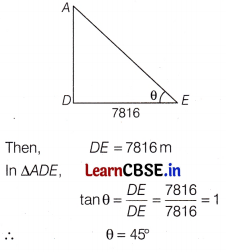
What is the angle of elevation if a man is standing at a distance of 7816 m from Nanda Devi?
Answer:

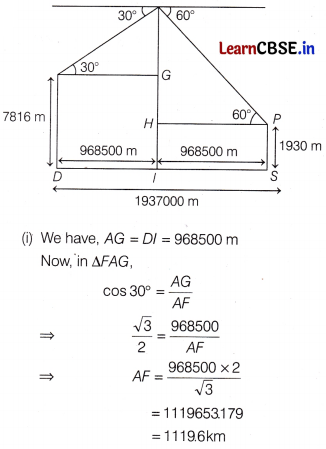
(ii) We have, HP = 1S = 968500 m
Now, in ∆FHP,
cos 60° = \(\frac{H P}{F P}\)
\(\frac{1}{2}\) = \(\frac{968500}{F P}\)
FP = 968500 × 2 = 1937000m
= 1937 km

(iii) In ∆FAG, tan 30° = \(\frac{F G}{A G}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{F G}{968500}\)
FG = \(\frac{968500}{\sqrt{3}}\)
= 559180.138 m
= 559.18 km
Height of satellite from ground
= FI = FG + GI
= 559.18 + 7.816 [∵ GH = AD = 7816 m]
= 566.996 km

Or

Let E be the position of man.