CBSE Sample Papers for Class 10 Maths Basic Set 6 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 6 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 6 with Solutions

Maximum Marks: 80
Time Allowed: 3 hours

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answers-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answers-IT (SA-II) type questions carrying 3 marks each
5. Section D has 4 Long Answers (LA) type questions carrying 5 marks each.
6. Section E has 3 source based/case based/passage based integrated units of assessment (4 marks each) with sub¬ parts of the values of 1,1 and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Qs of 5 marks has been given provided. An internal choice has been provided in 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7, wherever required if not stated.

Section – A(20 Marks)

Question 1.
HCE of 92 and 152 is
(A) 4
(B) 19
(C) 23
(D) 57
Solution:
(A) 4

Explanation: Prime factorisation of 92
= 2 × 2 × 23
Prime factorisation of 152 = 2 × 2 × 2 × 19
To find HCF, we multiply all the prime factors common to both numbers:
Therefore, HCF = 2 × 2 = 4

Question 2.
The product of a non-zero rational and an irrational number is
(A) always irrational
(B) always rational
(C) rational or irrational
(D) one
Solution:
(A) always irrational

Explanation: The product of a non-zero rational and an irrational number is always an irrational number.

Question 3.
The mode of the numbers 2, 3, 3, 4, 5, 4, 4, 5, 3, 4, 2, 6, 7 is: 1
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(c) 4
Explanation: Given data 2, 3, 3, 4, 5, 4, 4, 5, 3, 4, 2, 6, 7.
In the given data; 2 is 2 times, 3 is 3 times, 4 is 4 times, 5 is 2 times, 6 is 1 time, and 7 is 1 time.
So, mode of the data is 4.

Question 4.
The solution of the pair of linear equations x = -5 and y = 6 is
(A) (-5, 6)
(B) (-5, 0)
(C) (0, 6)
(D) (0, 0)
Solution:
(A) (-5, 6)

Explanation: Given that x = –5 and y = 6
The lines drawn for the given equations meet at (–5, 6) and Thus (–5, 6) is the solution of the given equations.

Question 5.
Which of the following equations has the sum of its roots as 3?
(A) 2x² – 3x + 6 = 0
(B) -x² + 3x – 3 = 0
(C) √2x² – \(\frac{3}{\sqrt{2}}\)x + 1 = 0
(D) 3x² – 3x + 3 = 0
Solution:
(B) -x² + 3x – 3 = 0

Explanation: –x² + 3x – 3 = 0
On comparing with ax² + bx + c = 0
a = –1, b = 3, c = –3
∴ Sum of the roots = -b/a = -3/-1 = 3

Question 6.
If in ∆ABC and ∆DEF, \(\frac{A B}{D E}=\frac{B C}{F D}\), then they will be similar, when
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Answer:
(c) ∠B = ∠D

Given, in ∆ABC and ∆DEF, \(\frac{A B}{D E}=\frac{B C}{F D}\)

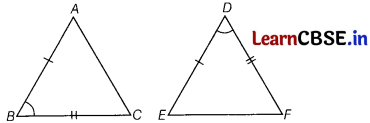
∆ABC and ∆EDF will be similar, if
∠B = ∠D [by SAS similarity criterion]

Question 7.
If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true?
(A) BC × EF = AC × FD
(B) AB × EF = AC × DE
(C) BC × DE = AB × EF
(D) BC × DE = AB × FD
Solution:
(C) BC × DE = AB × EF

Explanation: Since, ΔABC ~ ΔEDF, then we get
\(\frac{A B}{E D}=\frac{A C}{E F}=\frac{B C}{D F}\)
From first two, AB × EF = AC × DE. Option (B) is correct.
From last two, BC × EF = AC × FD. Option (A) is correct.
From first and last, BC × DE = AB × FD. Option (D) is correct

Question 8.
In the figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, the x =

(A) 10
(B) 9
(C) 8
(D) 7
Solution:
(B) 9

Explanation:
AS = AP = 5 cm, CQ = CR = 3 cm
BP = BQ, BQ + CQ = BC = 7 cm
BQ = 7 – 3 = 4 cm ⇒ BP = 4 cm
AB = x,  AP + BP = x
⇒ 5 + 4 = x
⇒ x = 9.

Question 9.
The length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle is: 1
(a) \(\frac{44}{3}\) cm
(b) \(\frac{88}{3}\) cm
(c) \(\frac{308{3}\) cm
(d) \(\frac{616}{3}\) cm
Answer:
(a) \(\frac{44}{3}\) cm
Explanation: Since, length of the arc of centre angle θ = \(\frac{\theta}{360}\) × 2πr
Length of the arc = \(\frac{60}{360}\) × \(\frac{2 \times 22}{7}\) × 14
\(\frac{44}{3}\) cm

Question 10.
If sin A + cos B = 1, A = 30° and B is an acute angle, then find the value of B.
(A) 45°
(B) 30°
(C) 90°
(D) 60°
Solution:
(D) 60°

Explanation: sin 30° + cos B = 1
\(\frac{1}{2}\) + cos B = 1
∴ cos B = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
i.e., cos B = cos 60° [∴ cos 60° = \(\frac{1}{2}\)]
Hence, ∠B = 60°.

Question 11.
If the height of a vertical pole is √3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
Solution:
(B) 60°

Explanation: Let the length of shadow is x,
The height of pole = √3 x
Now,

Question 12.
The area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm, is
(a) 16.5 cm²
(b) 17.5 cm²
(c) 19.62 cm²
(d) 8.75 cm²
Answer:
(d) 8.75 cm²

We know that area of sector A of radius r and length of arc l is given by
A = \(\frac{1}{2}\) lr
A = \(\frac{1}{2}\) × 3.5 × 5
= 8.75 cm²

Question 13.
In a right circular cone, the cross-section made by a plane parallel to the base is a
(A) circle
(B) frustum of a cone
(C) sphere
(D) hemisphere
Solution:
(A) circle

Explanation: In a right circular cone, if any cut is made parallel to its base, we get a circle.

Question 14.
If the circumference of a circle and the perimeter of a square are equal, then
(A) Area of the circle = Area of the square
(B) Area of the circle > Area of the square
(C) Area of the circle < Area of the square
(D) Nothing definite can be said about the relation between the areas of the circle and square.
Solution:
(B) Area of the circle > Area of the square

Explanation: According to question,
Circumference of a circle = Perimeter of square
Let ‘r’ and ‘a’ be the radius of circle and side of square.
2πr = 4a

A₁ > A₂
Area of circle is greater than the area of square.

Question 15.
If the pair of linear equations x – y = 1, x + ky = 5 has a unique solution x = 2, y = 1, then the value of k is: 1
(a) -2
(b) -3
(c) 3
(d) 4
Answer:
(c) 3
Explanation: Given equations are x – y = 1 and x + ky = 5.
Given solutions are x = 2, y = 1, these solutions must satisfy given equations.
So, putting x = 2, y = 1 in x + ky = 5,
we get;
2 + k = 5
⇒ k = 3
Also, equations have unique solutions, then:
\(\frac{1}{1} \neq \frac{-1}{k}\)
⇒ k ≠ -1, so k = 3

Question 16.
If x_i‘s are the mid-points of the class intervals of grouped data, f_i’s are the corresponding frequencies and x̄ is the mean, then (f_ix_i – x) is equal to
(A) 0
(B) -1
(C) 1
(D) 2
Solution:
(A) 0

Question 17.
Slant height of a cone if the radius is 7 cm and the height is 24 cm _______.
(A) 26 cm
(B) 25 cm
(C) 52 cm
(D) 62 cm
Solution:
(B) 25 cm

Explanation: Slant height of cone,
l = \(\sqrt{r^2+h^2}\)
Hence, r = 7 cm and h = 24 cm
∴ l = \(\sqrt{(7)^2+(24)^2}\)
= √625 = 25 cm

Question 18.
If radius of circle is 8 cm and tangent is drawn from an external point to the circle is 15 cm, then the distance from centre of circle to the external point is
(a) \(\sqrt{241}\) cm
(b) 17 cm
(c) 10 cm
(d) None of these
Answer:
(b) 17 cm

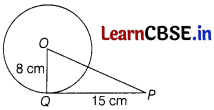
In right angled ∆OPQ,
using Pythagoras theorem
OP = \(\sqrt{O Q^2+Q P^2}\)
= \(\sqrt{8^2+15^2}\)
= \(\sqrt{64+225}\)
= \(\sqrt{289}\)
= 17 cm

Directions: A Statement of Assertion (A) is followed by a statement of Reason (R) in the following questions.
Mark the correct choice as.

Question 19.
Assertion (A): Co prime numbers are those numbers that have only one common factor, which is 1.
Reason (R): 0 is a rational number.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).

Explanation: Here, Both Assertion and Reason are true.
But Reason is not the correct explanation of assertion.

Question 20.
Assertion (A): The point A is on the y-axis at a distance of 4 units above from the origin. If the coordinates of the point B are (-3, 0). Then length of AB is 5 units.
Reason (R): Distance between points A(x₁, y₁) and B(x₂, y₂) is \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\).
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).

Explanation: If the point A is above the origin then is coordinates are (0, 4)
To find the distance AB we need to apply formula

Therefore, Both A and R are true and R is the correct explanation for A.

Section – B(10 Marks)

Question 21.
Find the discriminant of the quadratic equation 3x² – 2x + \(\frac{1}{3}\) = 0 and hence find the nature of its roots.
OR
Find the root of the quadratic equation x² – x – 2 = 0. 2
Answer:
Given equation:
3x² – 2x + \(\frac{1}{3}\) = 0
Discriminant D = b² – 4ac
= (-2)² – 4 × 3 × \(\frac{1}{3}\)
= 4 – 4
= 0
So, roots are real and equal.
OR
Given equation:
x² – x – 2 = 0
⇒ x² – 2x + x- 2= 0
⇒ x(x – 2)x + 1(x – 2) = 0
⇒ (x – 2) (x + 1) = 0
⇒ x = 2, -1
So, the roots of the equation x² – x – 2 = 0 are 2 and -1.

Question 22.
In the given figure, two tangents TP and TQ are drawn to a circle with center O from an external point T. Prove that ∠PTQ = 2∠OPQ.

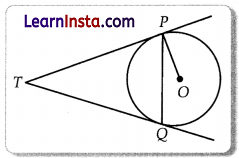
Solution:
Let ∠OPQ be θ, then
∠TPQ = 90° – θ
Since, TP = TQ
∠TQP = 90° – θ [opposite angles of equal sides]

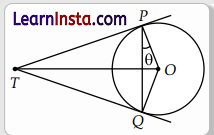
Now, ∠TPQ + ∠TQP + ∠PTQ = 180° [Angle sum property of a triangle]
⇒ 90° – θ + 90° – θ + ∠PTQ = 180°
⇒ ∠PTQ = 180° – 180° + 2θ
⇒ ∠PTQ = 2θ
Hence, ∠PTQ = 2 ∠OPQ
Hence Proved.

OR

In given figure, AB is the diameter of a circle with center O and AT is a tangent. If ∠AOQ = 58°, ∠ATQ.

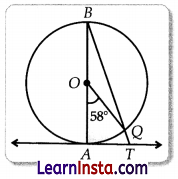
Solution:
∠AOQ = 58° (Given)
∠ABQ = \(\frac{1}{2}\)∠AOQ
[Angle on the circumference of the circle by the same arc]
= \(\frac{1}{2}\) × 58°
= 29°
∠BAT = 90° [∵ OA ⊥ AT]
∠ATQ = 90° – 29°
= 61°

Question 23.
In ABC, if X and Y are points on AB and AC respectively such that \(\frac{A X}{X B}\) = \(\frac{3}{4}\), AY = 5 and YC = 9, then state whether XY and BC parallel or not.
Solution:

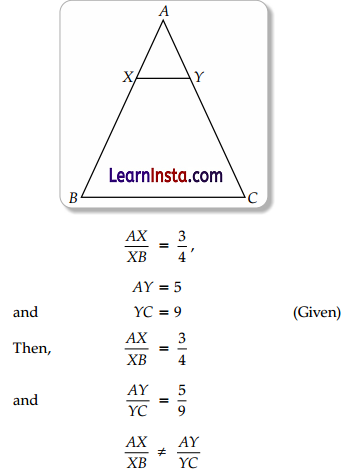
Hence, XY is not parallel to BC.

Question 24.
If one root of the quadratic equation 2x² + kx – 6 = 0 is 2, then find the value of k. Also, find the other root.
Answer:
Since, x = 2 is a root of the equation of 2x² + kx – 6 = 0
∴ 2×2² + 2k – 6 = 0
⇒ 8 + 2k – 6 = 0
⇒ 2k + 2 = 0
⇒ k = – 1
On putting k = – 1 in the equation 2x² + kx – 6 = 0, we get
2x² – x – 6 = 0
⇒ 2x² – 4x + 3x – 6 = 0
⇒ 2x (x – 2) + 3 (x – 2) = 0
⇒ (x – 2) (2x + 3) = 0
⇒ x – 2 = 0 or 2x + 3 = 0
⇒ x = 2 or – \(\frac{3}{2}\)
Hence, the other root is – \(\frac{3}{2}\).

Question 25.
What is the volume of a right circular cylinder of base radius 7 cm and height 10 cm? [Use π = 22/7]
Solution:
Here, r = 7 cm, h = 10 cm
Volume of cylinder = πr²h
= \(\frac{22}{7}\) × (7)² × 10
= 1540 cm³

OR

The rain water from 22 m × 20 m roof drains into cylindrical vessel of diameter 2 m and height 3.5 m. If the rain water collected from the roof fills (\(\frac{4}{5}\)) of cylindrical vessel then find the rainfall in cm.
Solution:
Volume of water collected in cylindrical vessel

Section – C(18 Marks)

Question 26.
144 cartons of Coke cans and 90 cartons of Pepsi cans are to be stacked in a canteen. If each stack is of the same height and if it contain equal cartons of the same drink, what would be the greatest number of cartons each stock would have ?
Solution:
Since, the greatest number of cartons is the HCF of 144 and 9o.
144 = 2⁴ × 3²
90 = 2 × 3² × 5
Therefore, HCF = 2 × 3² = 18
Thus the greatest number of cartons = 18.

Question 27.
If α, β are zeroes of the quadratic polynomial x² – 5x + 6, form another quadratic polynomial whose zeroes are \(\frac{1}{\alpha}, \frac{1}{\beta}\). 3
Answer:
Given that α and β are zeroes of x² – 5x + 6 = 0
x² – 5x + 6 = 0
⇒ x² – 3x – 2x + 6 = 0
⇒ x(x – 3) – 2(x – 3) = 0
⇒ (x – 3)(x – 2) = 0
⇒ x = 3, 2
Now, α = 3 and β = 2 then \(\frac{1}{\alpha}=\frac{1}{3}\) and \(\frac{1}{\beta}=\frac{1}{2}\)
Required equation: x² – (\(\frac{1}{3}\) + \(\frac{1}{2}\))x + \(\frac{1}{2}\) × \(\frac{1}{2}\) = 0
⇒ x² – \(\frac{5}{6}\)x + \(\frac{1}{6}\) = 0
⇒ 6x² – 5x + 1 = 0

Question 28.
In an A.E if sum of its first n terms is 3n² + 5n and its k^th term is 164, find the value of k.
Solution:
Here, Sn = 3n² + 5n
⇒ S₁ = 3.1² + 5.1 = 8 = a1
S₂ = 3.2² + 5.2
= 22 = a₁ + a₂
a₂ = 22 – 8 = 14
⇒ d = 6
a_k = 164
⇒ 8 + (k – 1)6 = 164
⇒ k = 27

OR

The sum of ages (in years) of a son and his father is 35 years and product of their ages is 150 years, find their ages.
Solution:
Let the age of father be x years and age of son be y years.
∴ x + y = 35 and xy = 150
Or y = 35 – x
Putting the value of y in xy = 150
x(35 – x) = 150
⇒ x² – 35x + 150 = 0
⇒ (x – 30)(x – 5) = 0
⇒ x = 30 or x = 5 (rejected)
⇒ y = 5
Hence, the age of father = 30 years and the age of son = 5 years.

Question 29.
In the figure, PQ is a tangent to a circle with centre O. If ∠OAB = 30°, find ∠ABP and ∠AOB.

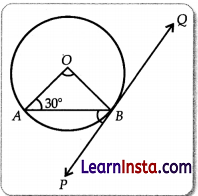
Solution:
In ΔOAB, OB = OA (radius of a circle)
Then, ∠OAB = ∠OBA
∠OBA = 30°
∴ ∠AOB = 180° – (30° + 30°)
∴ ∠AOB = 120°
∠ABP = ∠OBP – ∠OBA
= 90° – 30° = 60°

Question 30.
Find the roots of the following equation \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\), x ≠ – 4, 7.
Answer:
Given equation is \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\), x ≠ – 4, 7
⇒ \(\frac{(x-7)-(x+4)}{(x+4)(x-7)}=\frac{11}{30}\)
⇒ \(\frac{x-7-x-4}{x^2-7 x+4 x-28}=\frac{11}{30}\)
⇒ \(\frac{-11}{x^2-3 x-28}=\frac{11}{30}\)
⇒ \(\frac{-1}{x^2-3 x-28}=\frac{1}{30}\)
⇒ – 30 = x² – 3x – 28
⇒ x² – 3x + 2 = 0
On comparing with the standard quadratic equation
ax² + bx + c = 0, we get
a = 1, b = – 3 and c = 2
By using quadratic formula, we get
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{-(-3) \pm \sqrt{(-3)^2-4(1)(2)}}{2 \times 1}\)
= \(\frac{3 \pm \sqrt{9-8}}{2}\)
= \(\frac{3 \pm 1}{2}\)
x = \(\frac{3+1}{2}\) or x = \(\frac{3-1}{2}\)
⇒ x = \(\frac{4}{2}\) or x = \(\frac{2}{2}\)
∴ x = 2 or x = 1

Or

Solve for x, \(2\left(\frac{2 x+3}{x-3}\right)-25\left(\frac{x-3}{2 x+3}\right)\) = 5.
Answer:
Let \(\frac{2 x+3}{x-3}\) = y
Then, \(\frac{x-3}{2 x+3}=\frac{1}{y}\)
Therefore, the given equation reduces to
2y – 25 \(\frac{1}{y}\) = 5
⇒ 2y² – 25 = 5y
⇒ 2y² – 5y – 25 = 0
⇒ 2y² – 10y + 5y – 25 = 0 [byfactorisation method]
⇒ 2y (y – 5) + 5 (y – 5) = 0
⇒ (y – 5) (2y + 5) = 0
⇒ y = 5 or y = – \(\frac{5}{2}\)
Now, on putting y = 5 in Eq. (j), we get
\(\frac{2 x+3}{x-3}=\frac{5}{1}\)
⇒ 5 x -15 = 2x +3
⇒ 3x = 18
⇒ x = 6
Again, on putting y = – \(\frac{5}{2}\) in Eq. (i), we get
\(\frac{2 x+3}{x-3}=-\frac{5}{2}\)
⇒ – 5x + 15 = 4x + 6
⇒ 9x = 9
⇒ x = 1
Hence, the values of x are 1 and 6.

Question 31.
A box consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Ramesh, a shopkeeper will buy only those shirts which are good but ‘Kewal’ another shopkeeper will not buy shirts with major defects. A shirt is taken out of the box at random. What is the probability that:
(i) Ramesh will buy the selected shirt?
(ii) ‘Kewal’ will buy the selected shirt?
Solution:
(i) Number of good shirts = 88
P (Ramesh buys a shirt) = \(\frac{88}{100}\) or \(\frac{22}{25}\)

(ii) Number of shirts without major defect = 96
P (Kewal buys a shirt) = \(\frac{96}{100}\) or \(\frac{24}{25}\)

Section – D(20 Marks)

Question 32.
Two water taps together can fill a tank in 1\(\frac{7}{8}\) hours. The tap with longer diameter takes 2 hours less than the tap with smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
Solution:
Let the smaller tap fills the tank in x hours.
Therefore, the larger tap fills the tank in x – 2 hours.

Therefore, x = 5
Smaller and larger taps can fill the tank separately in 5 hours and 3 hours respectively.

OR

Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream.
Solution:
Let the speed of stream be x km/hr.
∴ Speed of boat upstream = (15 – x) km/hr
Speed of boat downstream = (15 + x) km/hr

⇒ 200 = 225 – x²
x = 5 (Rejecting – 5)
⇒ Speed of stream = 5 km/hr

Question 33.
The distribution below gives the weights of 30 students of a class. Find the median weight of the students: 5

Weight in kg	Number of Students
40 – 45	2
45 – 50	3
50 – 55	8
55 – 60	6
60 – 65	6
65 – 70	3
70 – 75	2

Answer:

Weight (in kg) (Cl.)	Number of students (fi)	Cumulative frequency (cf)
40 – 45	2	2
45 – 50	3	5 (= 2 + 3)
50 – 55	8	13 (= 5 + 8)
55 – 60	6	19 (= 13 + 6)
60 – 65	6	25 (= 19 + 6)
65 – 70	3	28 (= 25 + 3)
70 – 75	2	30 (= 28 + 2)

Here, Median number: \(\frac{N}{2}=\frac{30}{2}\) = 15
cf. just > median number (15) = 19
⇒ Median class = The class interval corresponding to c.f. of 19
⇒ Median class = 55 – 60
Lower limit of the median class, l = 55
Frequency of the median class, f_m = 6
Size of the median class, h = 5 (= 60 – 55)
Cumulative frequency of the pre-median class, C = 13
We know that,
Median = l + \(\frac{h}{f_m}\)(\(\frac{N}{2}\) – C)
Median = 55 + \(\frac{5}{6}\) × (15 – 13)
= 55 + \(\frac{5}{6}\) × 2
= 55 + \(\frac{5}{3}\)
= 50 + 1.67 = 51.67
Thus, the required median weight of students is 51.67 kg.

Question 34.
Isha is 10 years old girl. On the result day, Isha and her father Suresh were very happy as she got first position in the class. While coming back to their home, Isha asked for a treat from her father as a reward for her success.
They went to a juice shop and asked for two glasses of juice.
Aisha, a juice seller, was serving juice to her customers in two type of glasses. Both the glasses had inner radius 3 cm. The height of both the glasses was 10 cm.
First type: A Glass with hemispherical raised bottom.

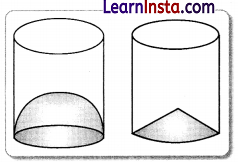
Second type: A glass with conical raised bottom of height 1.5 cm.
Isha insisted to have the juice in first type of glass and her father decided to have the juice in second type of glass. Out of the two, Isha or her father Suresh, who got more quantity of juice to drink and by how much?
Solution:
Capacity of first glass = πr²H – \(\frac{2}{3}\)πr³
= π × 9(10 – 2)
= 72π cm³
Capacity of second glass = πr²H – \(\frac{1}{3}\)πr³
= π × 3 × 3(10 – 0.5)
= 85.5π cm³
∵ Suresh got 42.43 cm³ more quantity of juice.

Detailed Solution:
In case of first type glass, we have
radius (r) = 3 cm
Height (H) = 10 cm
Capacity of Juice in cylindrical part = πr²H
= π × (3)² × 10

= 226.28 cm³ (Approx.)
In case of second glass, we have
radius of base (r) = 3 cm
height of bottom part (h) = 1.5 cm

= 268.71 cm³ (Approx.)
Since, Suresh used second glass for drinking juice,
so he got more quantity of juice.
i.e., Suresh got 268.71 – 226.28 = 42.43 cm³ more juice than Isha.

OR

From a solid cylinder of height 5.6 cm and diameter 2.8 cm, a conical cavity of same height and same diameter is hollowed out. Find the volume of the remaining solid.
Solution:

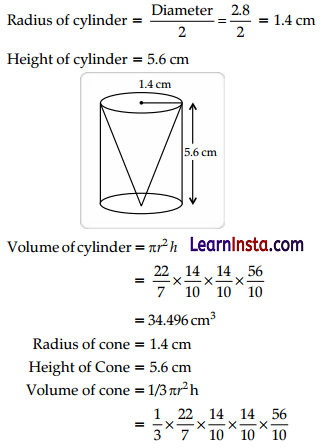
= 11.498 cm³
Volume of remaining solid = Volume of cylinder – Volume of cone
= 34.496 – 11.498
= 22.998 = 23 cm³ (approx.)

Question 35.
On annual day of a school, 400 students participated in the function. Frequency distribution showing their ages is as shown in the following table:

Find mean and median of the above data.
Solution:

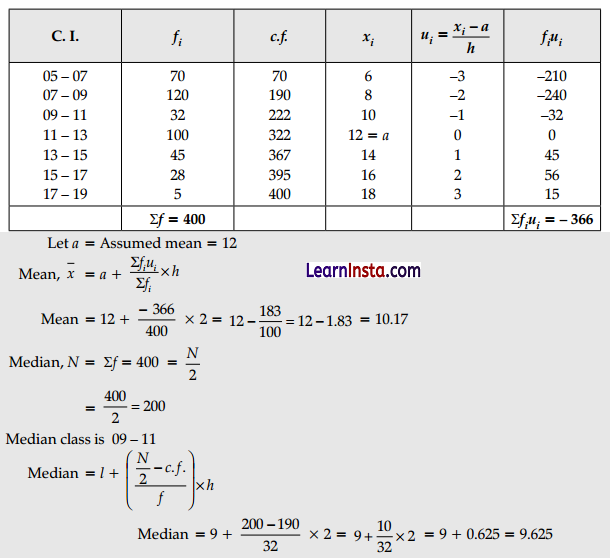
Section – E(12 Marks)

Question 36.
Roller Coaster Polynomials

Polynomials are everywhere. They play a key role in the study of algebra in analysis and on the whole many mathematical problems involving them.
Since polynomials are used to describe curves of various types engineers use polynomials to graph the curves on roller coasters.

Based on the above information, answer the following questions.
(i) If the roller coaster is represented by the following graph y = p (x), then name the type of the polynomial it traces.

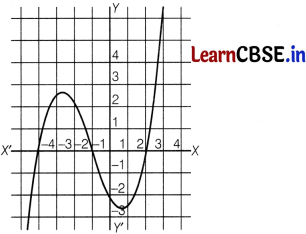
Answer:
Since, graph of given polynomial intersect X-axis at 3 points.
So, it has three zeroes.
Hence, it is a cubic polynomial.

(ii) If p(x) = 2x³ – 5x² – 14x + 8, then find the sum and product of zeroes.
Answer:
On comparing given polynomial 2x³ – 5x² – 14x + B with ax³ + bx² + cx + d, we get
a = 2, b = – 5, c = – 14 and d = 8
Sum of roots, α + β + γ = \(\frac{-b}{a}\)
= \( \frac{-(-5)}{2}\)
= \( \frac{5}{2}\)

Product of roots, αβγ = \(\frac{-d}{a}\)
= \( \frac{-8}{2}\)
= – 4

Or

Find a quadratic polynomial, the sum and product of whose roots are – 3 and 2, respectively.
Answer:
Sum of roots, α + β = – 3
= \(\frac{-b}{a}\)
and product of roots. αβ = 2
= \(\frac{c}{a}\)
∴ Quadratic polynomial is x² + 3x +2.

(iii) In the graph shown above, find the zeroes of y = p (x).
Answer:
The graph of given polynomial intersect X-axis at points – 4, – 1 and 2.
So, zeroes of given polynomial are – 4, – 1 and 2.

Question 37.
Shreya purchased a new table from market with her mother. The top of the table is hexagonal in shape as shown in the given figure.

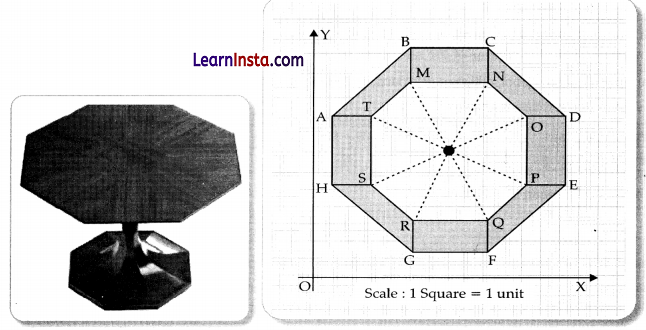
(i) Find the coordinates of points H and G.
(ii) Write one pair of points which have same ordinate.
(iii) Find the distance between the points A and B.
OR
Find the coordinates of the line joining points M and Q.
Solution:
(i) Coordinates of point H = (1, 5)
Coordinates of point G = (5, 1)
(ii) Points T and O has same ordinates i.e., T = (3, 9)
and O = T = (11, 9)
(iii) Coordinates of points A = (1, 9)
Coordinates of point B = (5, 13)
Distance, d = \(\sqrt{(1-5)^2+(9-13)^2}\)
= \(\sqrt{16+16}\)
= √32
= 4√2 units.

OR

Coordinates of point M = (5, 11)
Coordinates of point Q = (9, 3)
Mid-point = \(\left(\frac{5+9}{2}, \frac{11+3}{2}\right)\)
= (7, 7)

Question 38.
Read the following text and answer the following questions on the basis of the same:
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle are also equiangular; that is, all three internal angles area also congruent to each other and are each 60°. Here we have an equilateral triangle which is inscribed in a circle of radius 6 cm.

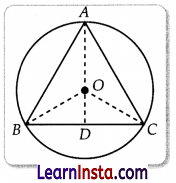
(i) What is the length of BD?
Solution:
ABC be an equilateral triangle.
∴ OA = OB = OC = 6 cm (given)
D is the mid-point of BC and BO & CO are bisectors of ∠B and ∠C.

Hence, the length of BD is 3√3 cm.

(ii) Find the side of this equilateral triangle.
Solution:
We have proved that
BD = 3√3 cm
Then, BC = 2 × BD
= 2√3 × 3
= 6√3 cm.

(iii) Find the length of OD.
OR
Find the length of AD.
Solution:
Here, OB = 6 cm and BD = 3√3 cm

⇒ 2AD = 18
⇒ AD = 9 cm.