CBSE Sample Papers for Class 10 Maths Basic Set 5 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 5 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 5 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:
1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answers-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answers-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answers (LA) type questions carrying 5 marks each.
6. Section E has 3 source-based/case-based/passage-based integrated units of assessment (4 marks each) with sub-parts of the values of 1, 1, and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks, and 2 Qs of 5 marks has been given provided. An internal choice has been provided in 2-mark questions of Section E.
8. Draw neat figures wherever required, Take. x = 2, wherever required if not stated.

Section-A(20 Marks)

Question 1.
If a and b are co-prime numbers, then find the HCF (a, b).
(A) 2
(B) 1
(C) 0
(D) None of these
Solution:
(B) 1
Explanation: Since, 1 is the only common factor of co-prime numbers.
Thus, HCF (a, b) = 1

Question 2.
What will be the simplest form of \(\frac{\sqrt{45}+\sqrt{20}}{\sqrt{5}}\) ?
(A) 5√5
(B) 5
(C) 25
(D) √5
Solution:
(B) 5
Explanation: \(\frac{3 \sqrt{5}+2 \sqrt{5}}{\sqrt{5}}=\frac{5 \sqrt{5}}{\sqrt{5}}\) = 5

Question 3.
The value of k, for which the pair of linear equations x + y – 4 = 0, 2x + ky – 3 = 0 have no solution, is: 1
(a) 0
(b) 2
(c) 6
(d) 8
Answer:
(b) 2
Explanation: For no solution, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Here,
a₁ = 1, b₁ = 1, c₁ = -4 and a₂ = 2, b₂ = k,
c₂ = -3
Now, \(\frac{1}{2}=\frac{1}{k} \neq \frac{-4}{-3}\)
⇒ k = 2

Question 4.
What about the number of solutions if the given system of equations represents coincident lines?
(A) One solution
(B) Infinite or many solutions
(C) No solution
(D) None of these
Solution:
(B) Infinite or many solutions
Explanation: As we know, Each point on the Coincident line will be a solution for a given pair of linear equations, So, infinite or many solutions exists.

Question 5.
Aruna has only ₹ 1 and ₹ 2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ₹ 75, then the number of ₹ 1 and ₹ 2 coins are, respectively :
(A) 35 and 15
(B) 35 and 20
(C) 15 and 35
(D) 25 and 25
Solution:
(D) 25 and 25
Explanation: Let the number of ₹ 1 coins = x and the number of ₹ 2 coins = y
So, according to the question,
x + y = 50 ….(i)
x + 2y = 75 ….(ii)
Subtracting equation (i) from (ii) y = 25
Substituting value of y in (i) x = 25
So, y = 25 and x = 25.

Question 6.
If the length of the shadow of a building is decreasing, then the angle of elevation is
(a) decreasing
(b) increasing
(c) remains same
(d) None of these
Answer:
(b) increasing

Here, AB is the building and BE is the initial length of the shadow.

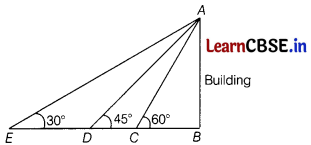
As the shadow reaches from E to C the angle of elevation increases from 30° to 60°.

Question 7.
In the following figure, ST || QR, point S divides PQ in the ratio 4: 5. If ST = 1.6 cm, what is the length of QR?

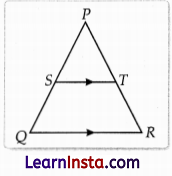
(Note: The figure is not to scale.)
(A) 0.71 cm
(B) 2 cm
(C) 36 cm
(D) (cannot be calculated from the given data.)
Solution:
(C) 36 cm
Explanation:

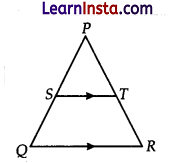
As given, ST is parallel to QR then in triangle PST and ΔPQR, ∠S = ∠Q and ∠T = ∠R (corresponding angle)
Therefore, ΔPST and ΔPQR are similar by (AA)
Now, \(\frac{P S}{P Q}=\frac{S T}{Q R}\) = (As we know ratio of corresponding sides of similar triangles are always equal)

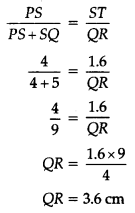
Question 8.
In the given figure, if ∠A = 90°, ∠B = 90°, OB = 45cm, OA = 6 cm and AP = 4 cm, then find QB.

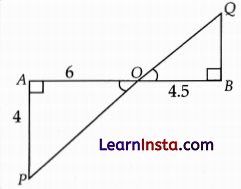
(A) 1 cm
(B) 2 cm
(C) 3 cm
(D) 4 cm
Solution:
(C) 3 cm
Solution:
(C) 3 cm

Question 9.
If P(E) = 0.65, then the value of P(not E) is: 1
(a) 1.65
(b) 0.25
(c) 0.65
(d) 0.35
Answer:
(d) 0.35
Explanation: Given, P(E) = 0.65,
then P(notE) = 1 – 0.65 = 0.35 [∵ P(E) + P(not E) = 1]

Question 10.
If sec θ + tan θ = p, then tan θ is
(A) \(\frac{p^2+1}{2 p}\)
(B) \(\frac{p^2-1}{2 p}\)
(C) \(\frac{p^2-1}{p^2+1}\)
(D) \(\frac{p^2+1}{p^2-1}\)
Solution:
(B) \(\frac{p^2-1}{2 p}\)
Explanation: sec θ + tan θ = p is the given equation.
Since, 1 + tan² θ = sec² θ
Or, sec θ = \(\sqrt{1+\tan ^2 \theta}\)
Put this value of sec θ in equation (i), we get
\(\sqrt{1+\tan ^2 \theta}\) + tan θ = p
Or, \(\sqrt{1+\tan ^2 \theta}\) = p – tan θ
On squaring both sides, we get
1 + tan² θ = p² + tan² θ – 2p tan θ
Or, 1 = p² – 2p(tan θ)
Or, 1 – p² = -2p(tan θ)
Or, tan θ = \(\frac{p^2-1}{2 p}\)

Question 11.
The value of 9 sec² A – 9 tan² A is
(A) 1
(B) 9
(C) 8
(D) 0
Solution:
(B) 9
Explanation:
9sec² A – 9tan² A =  9(sec² A – tan² A)
= 9(1) = 9

Question 12.
If the system of equations 5x + 2 y = k and 10x + 4y = 3 has infinitely many solutions, then the value of k is
(a) \(\frac{3}{2}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{3}\)
(d) 2
Answer:
(a) \(\frac{3}{2}\)

Given, a system of equations is
5x + 2y = k
and 10x + 4y =3
Here a₁ =5, b₁ = 2, c₁ = – k
and a₂ = 10, b₂ = 4, c₂ = – 3
For infinitely many solutions, we must have
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
⇒ \(\frac{5}{10}=\frac{2}{4}=\frac{-k}{-3}\)
⇒ \(\frac{1}{2}=\frac{1}{2}=\frac{k}{3}\)
⇒ \(\frac{1}{2}=\frac{k}{3}\)
⇒ k = \(\frac{3}{2}\)

Question 13.
If the volume of a cube is 8 cm³, then the total surface area is
(A) 24 cm²
(B) 384 cm²
(C) 48 cm²
(D) 40 cm²
Solution:
(A) 24 cm²
Explanation: Volume of cube = 8 cm³
a³ = 8
a³ = 2³
a = 2 cm
total surface area of cube = 6a²
= 6(2)²
= 6(4)
= 24 cm²

Question 14.
The area of a sector for a circle of radius 1.4 cm and central angle 90° is:
(A) 154 cm²
(B) 154 cm²
(C) 3.08 cm²
(D) 308 cm²
Solution:
(A) 154 cm²
Explanation: The area of the sector
\(\begin{aligned}
& =\frac{\theta}{360^{\circ}} \times \pi r^2 \\
& =\frac{90^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 1.4 \times 1.4
\end{aligned}\) = 1.54 cm²

Question 15.
The vertices of a triangle OAB are 0(0, 0), A(4, 0) and B(0, 6). The median AD is drawn on OB. The length of AD is:

(a) \(\sqrt{52}\) units
(b) 5 units
(c) 25 units
(d) 10 units
Answer:
(b) 5 units
Explanation:

Given that AD, is median.
So, D is the mid-point of OB.
Coordinates of D = (\(\frac{0+0}{2}\), \(\frac{0+6}{2}\)) = (0, 3)
Using distance formula:
Length of AD = \(\sqrt{(4-0)^2+(0-3)^2}\)
= \(\sqrt{4^2+3^2}\)
= \(\sqrt{16+9}\)
= \(\sqrt{25}\)
= 5 units

Question 16.
The mode of the numbers 2, 3, 3, 4, 5, 4, 4, 5, 3, 4, 2, 6, and 7 is:
(A) 2
(B) 3
(C) 4
(D) 5
Solution:
(C) 4
Explanation: Mode = 4 (occurring most number of times)

Question 17.
A cylinder, a cone, and a hemisphere have same base and same height. The ratio of their volumes is ……
(A) 1:3:3
(B) 3:3:1
(C) 3:1:2
(D) 2:1:3
Solution:
(C) 3:1:2
Explanation: Ratio of volumes = Volume of cylinder
∴ Volume of cone: Volume of the hemisphere
\(\begin{aligned}
& =\pi r^2 r: \frac{1}{3} \pi r^2 r: \frac{2}{3} \pi r^3 \quad[r=h] \\
& =1: \frac{1}{3}: \frac{2}{3}
\end{aligned}\)  (each term is divide by πr³
= 3:1:2

Question 18.
A month is selected at random in a year, the probability that it is March or October is
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{6}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{1}{6}\)

There are 12 months in a year.
∴ Required probability = \(\frac{2}{12}=\frac{1}{6}\)

Directions: A Statement of Assertion (A) is followed by a statement of Reason (R) in the following questions. Mark the correct choice as.

Question 19.
Assertion (A): If the distance between the point (4, p) and (1, 0) is 5, then the value of p is 4.
Reason (R): The point which divides the line segment joining the points (7, -6) and (3, 4) in ratio 1: 2 internally lies in the fourth quadrant.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) gives the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
(C) Assertion (A) is true but Reason (R) is false.
(D) Assertion (A) is false but Reason (R) is true.
Solution:
(B) Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Explanation: In case of assertion: Distance between two points (x_1, y₁) and (x₁, y₂) is given as d = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
where, (x_1, y₁) = (4, p)
(x₁, y₂) = (1, 0)
And d = 5
Put the values, we have
5³ =(1 – 4)³ + (0 – p)³
25 = (-3)³ + (-p)³
25 – 9 = p³
16 = p³
p = ± 4, As given p = 4 is correct.
∴ The assertion is true.
In case of reason: Let (x, y) be the point

So, the required point (x, y) = (\(\frac{17}{3},-\frac{8}{3}\) lies in IVth quadrant.
∴ Reason is correct.
Hence, Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).

Question 20.
Assertion (A): LCM of 200 and 240 is 1200.
Reason (R): HCF of two co-prime numbers is 1.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) gives the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
(C) Assertion (A) is true but Reason (R) is false.
(D) Assertion (A) is false but Reason (R) is true.
Solution:
(B) Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Explanation: Prime factorisation of 200 = 2³ × 5² and 240 = 24 × 3 × 5¹
LCM (200, 240) = 2⁴ × 3 × 5² = 1200
So, the assertion is true.
HCF of co-prime numbers indeed is 1.
Therefore, Both A and R are true but R is not the correct explanation of A.

Section-B(10 Marks)

Question 21.
The probability of happening of an event is 0.02. The probability of not happening of the event is:
(a) 0.02
(b) 0.80
(c) 0.98
(d) \(\frac{49}{100}\)
Answer:
(c) 0.98
Explanation: Given the probability of happening an event = 0.02
Then, the Probability of not happening of the event = 1 – 0.02 = 0.98 [∵ P(E) + P(not E) = 1]

Question 22.
In the given figure, PQ and PR are tangents to the circle with centre O such that ∠QPR = 60°, then find ∠OQR.

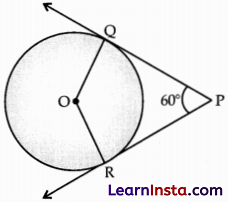
Solution:
∠QPR = ∠60°(Given)
∠QOR + ∠QPR = 180° (supplementary angles)
∴ ∠QOR = 180° – 60° = 120°

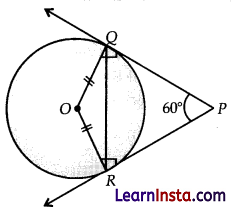
From ΔOQR,
∠OQR + ∠ORQ + ∠QOR = 180
(Angle sum property of triangle)
∠OQR + ∠OQR + 120 = 180
(∠OQR = ∠ORQ, Opposite angles of equal sides )
∠OQR + ∠OQR = 180 – 120 2∠OQR = 60, ∠OQR = \(\frac{60}{2}\) = 30°

OR

Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ
Solution:

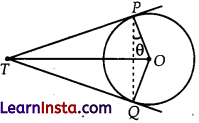
Let ∠OPQ be θ.
∴ ∠TPQ =∠OPT – ∠OPQ
∴ ∠TPQ = (90°- 0)
(∠OPT = 90 , The radius of the circle and tangent are perpendicular to each other at the point of contact)
Since TP = TQ (Tangents)
∴ ∠TQP = (90° – θ) (Opposite angles of equal sides)
Now, ∠TPQ + ∠TQP + ∠PTQ = 180°
⇒ 90° – θ + 90°- θ + ∠PTQ = 180°
⇒ ∠PTQ = 180° -180° + 2θ
⇒ ∠PTQ = 2θ
⇒ ∠PTQ = 2∠OPQ. Hence proved.

Question 23.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{A O}{B O}=\frac{C O}{D O}\)
Solution:

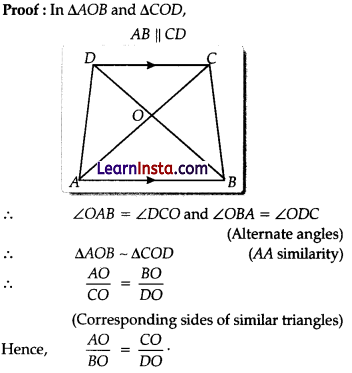
Question 24.
If the mean of x and \(\frac{1}{x}\) is M, then what is the value of mean of x³ and \(\frac{1}{x^3}\)?
Answer:
Given, mean of x and \(\frac{1}{x}\) is M.

Question 25.
Find the perimeter of a quadrant of a circle of radius 14 cm.
Solution:
Perimeter of a quadrant = 2(Radius) + Pad\(\frac{\theta}{360}\) × 2πr
= 2(14) + = \(\frac{90}{360}\) x2x \(\frac{22}{7}\) x14 [For quadrant, 0 = 90°]
= 28 + \(\frac{90}{360}\) × 88
= 28 + 22
= 50 cm

OR

Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
Solution:
Let radius of first circle = R = 24 cm and radius of second circle = r = 7 cm
And let radius of third circle = A cm
Area of first circle = πR² = π(24)² = 576 π cm²
Area of second circle = πr” = π(7)² = 49 π cm²
Area of third circle = Area of first circle + Area of second circle
πA² = 576 π + 49 π
Or, A = 625
Or, A=25cm
Therefore, radius of third circle = 25 cm.

Section -C(18 Marks)

Question 26.
Prove that √2 is an irrational number.
Solution:
Let us assume √2 be a rational number and its simplest form be a/b, a and b are co-prime positive integers and b ≠ 0.
So, √2 = a/b
⇒ a² = 2b²
Thus a² is a multiple of 2
⇒ a is a multiple of 2
Let a = 2 m for some integer m
b² = 2m²
Thus, b² is a multiple of 2
⇒ b is a multiple of 2
Hence, 2 is a common factor of a and b.
This contradicts the fact that a and b are co-primes
Hence, √2 is an irrational number.

Question 27.
The solution of the pair of linear equations x = -5 and y = 6 is: 1
(a) (-5, 6)
(b) (-5, 0)
(c) (0, 6)
(d) (0, 0)
Answer:
(a) (-5, 6)
Explanation: x = -5 represents a line parallel to the y-axis and y = 6 represents a line parallel to the x-axis
So, point of intersection must have x = -5 and y = 6, and both the lines intersect at (-5, 6).

Question 28.
Find the quadratic polynomial, the sum and product of zeroes are -3 and 2 respectively. Hence find the zeroes.
Solution:
Sum of zeroes = -3 and Product of zeroes = 2
The quadratic polynomial will be x² – (Sum of zeroes)
x + Product of zeroes
x² – (-3z) + 2 = 0
x² + 3x + 2 = 0
x² + 2x + x + 2 = 0
x(x + 2) +1 (x + 2) = 0
(x + 2)(x + 1) = 0
x = -2 and -1

OR

Find the zeroes of the quadratic polynomial x² – 2√2x and verify the relationship between the zeroes and the coefficients.
Solution:
We know that, p(x) = x² – 2√2x
⇒ x(x – 2√2) = 0
⇒ x = 0 & 2√2
Sum of zeroes = 0 + 2√2 = 2√2
Product of zeroes = (0) × ( 2√2, ) = 0
Sum of zeroes = -b/a = 2√2
Product of zeroes = c/a = 0

Question 29.
In given fig., two circles touch each other at the point C. Prove that the common tangent to the circles at C, bisects the common tangent at P and Q.

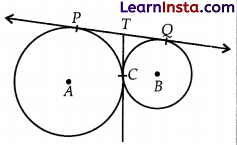
Solution:
Since PT = TC  ….(i)
and QT = TC   ….(ii) [tangents of circle from external point]
So, PT = QT [from eq (i) and eq (ii)]
Now, PQ = PT + TQ
⇒ PQ = PT + PT
⇒ PQ = 2PT
⇒ 1/2 PQ = PT = TQ

Question 30.
A circle is touching the side BC of ∆ABC at P and touching AB and AC produced at Q and R, respectively. Prove that AQ = \(\frac{1}{2}\) (Perimeter of ∆ABC).
Answer:
Since tangents from an exterior point to a circle are equal in length.
∴ BP = BQ [from B] ……………(i)
CP = CR [from C] ……………..(ii)
and AQ = AR [from A] ………….(iii)
From Eq. (ii), we have
AQ = AR

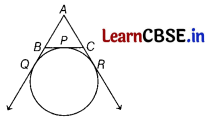
⇒ AB + BQ = AC + CR
⇒ AB + BP = AC + CP [using Eqs. (i) and (ii)] ………………… (iv)
Now, Perimeter of ∆ABC= AB + BC + AC
⇒ Perimeter of ∆ABC = AB + (BP + PC) + AC
⇒ Perimeter of ∆ABC = (AB + BP) + (AC + PC)
⇒ Perimeterof ∆ABC = 2 (AB + BP) [using Eq. (iv)]
⇒ Perimeter of ∆ABC = 2 (AB + BQ) [using Eq. (i)]
⇒ Perimeter of ∆ABC = 2AQ
∴ AQ = \(\frac{1}{2}\) (Perimeter of ∆ABC)
Hence proved.

Or

The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
Answer:
Let the line BD intersects the bigger circle at E.
Now, Join AE.
Let O be the centre of the bigger circle, then O is the mid-point of AB.
[∵ AB is a diameter of the bigger circle]

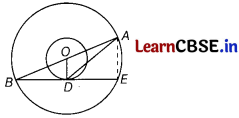
BD is a tangent to the smaller circle andOD s a radius through the point of contact D.
Then,
OD ⊥ BD
⇒ OD ⊥ BE
Since, OD is perpendicular to a chord BE of bigger circle.
∴ BD = DE
[∵ perpendicular drawn from the centre to a chord bisects the chord]
D is the mid-point of BE.
∴ In ∆BAE, O is the mid-point of AB
and D is the mid-point of BE.
∴ OD = AE
[∵ line segment joining the mid-points of any two sides of a triangle is half of the third side]
⇒ AE = 2 (OD)
= 2 × 8
= 16 cm
In right angled ∆OBD. use Pythagoras theorem,
OD² + BD² = OB²
BD = \(\sqrt{O B^2-O D^2}\)
= \(\sqrt{(13)^2-(8)^2}\)
= \(\sqrt{169-64}\)
= \(\sqrt{105}\)
∴ DE = BD = \(\sqrt{105}\) cm
In right angled ∆AED, using Pythagoras theorem, we have
AD = \(\sqrt{A E^2+D E^2}\)
= \(\sqrt{(16)^2+(\sqrt{105})^2}\)
= \(\sqrt{256+105}\)
= \(\sqrt{361}\)
= 19 cm

Question 31.
From all the two digit numbers a number is chosen at random. Find the probability that the chosen number is a multiple of 7.
Solution:
All possible outcomes are 10, 11, 12 ….. 98, 99.
No. of all possible outcomes = 90.
All favourable outcomes are 14, 21, 28 …. 98
No. of favourable outcomes = 13
∴ P(getting a number multiple of 7) = 13/90

Section -D(20 Marks)

Question 32.
For what values of a and b does the following pair of linear equations have infinite number of solutions?
2x + 3y = Z and a(x + y)—b(x-y) = 3a + b – 2.
Solution:
For equation
2x + 3y – 7 =0
a₁ = 2, b₁ = 3 and c₁ = -7
and a(x + y)-b (x – y) = 3a + b – 2
ax + ay – bx + by = 3a + b – 2
(a – b) x + (a + b) y- (3a + b – 2) = 0
a₂ = a – b, b₂ = a + b and c₂ = -(3a + b – 2)
For infinitely many solutions

OR

(a) Solve for x:\(\frac{x}{x-1}+\frac{x-1}{x}\) whole \(\frac{1}{4}\), x ≠ 0,1.
(b) Is 1 a root for the quadratic equation, \(\frac{1}{x-1}=\frac{2}{x-2}\) +4?
Solution:

\(\frac{2 x^2-2 x+1}{x^2-x}=\frac{17}{4}\)
4(2x² – 2x + 1) = 17(x² – x)
8x² – 8x + 4 = 17x² – 17x
9x² – 9x – 4 =0
9x² – (12-3)x – 4 = 0
9x² – 12x + 3x – 4 = 0
3x(3x – 4) + 1(3x – 4) = 0
(3x – 4)(3x + 1) = 0
3x – 4 = 0,  3x + 1 = 0
3x = 4,    3x = -1
x = 4/3   x = -1/3
(b) No. because \(\frac{1}{x-1}\) is not defined for x = 1

Question 33.
From an external point P, a tangent PT and a line segment PAB is drawn to a circle with centre O. ON perpendicular on the chord AB. Prove that:
(A) PA.PB = PN² – AN²
(B) PN² – AN² = OP² – OT²
(C) PA. PB = PT²

OR
In the given figure, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.

Answer:

(A) L.H.S = PA-PB
= (PN – AN) (PN + BN)
= (PN – AN) (PN + AN) [∵ ON ⊥ AB .-. N is the mid-point of AB]
= PN² – AN² = R.H.S

(B) In right triangle PNO,
OP² = ON² + PN² [By Pythagoras theorem ]
⇒ PN² = OP² – ON²
Now, LH.S = PN² – AN²
= (OP² – ON²) – AN²
= OP² – (ON² + AN²)
= OP² – OA² [Using Pythagoras theorem in ΔONA]
= OP² – OT² = R.H.S [Radii of the same circle]

(C) From (i) and (ii), we have
PA.PB = PN² – AN² and
PN² – AN² = OP² – OT²
∴ PA.PB = OP² – OT² …….. (i)
In right angle ΔOTP,
OP² = OT² + PT² [By Pythagoras theorem]
⇒ OP² – OT² = PT²
∴ PA.PB = PT² …….. (ii)
∴ PA.PB = PT² [Using (i) and (ii)]
OR
Let, BL = x
⇒ BN = x
[∵ Tangents drawn from an external point to the circle are equal in length]
∴ CL = CM = 8 – x [∵ BC = 8 cm]
and AN = AM = 10 = x [∵ AB = 10 cm]
Now, AC = 12 cm
∴ AM + MC = 12
⇒ 10 – x + 8 – x = 12
⇒ 18 – 2x = 12
⇒ 6 = 2x
⇒ x = 3
∴ Length of BL = 3 cm
Length of CM = 8 – 3 = 5 cm
Length of AN = 10 – 3 = 7 cm

Question 34.
A solid is in the shape of a hemisphere surmounted by a cone. If the radius of hemisphere and base radius of cone is 7 cm and height of cone is 3.5 cm, find the volume of the solid. (Use π = \(\frac{22}{7}\))
Solution:

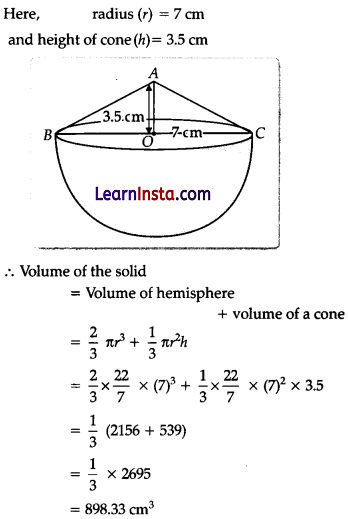
OR

Water is flowing at the rate of 15 km/h through a cylindrical pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time the level of water in pond rise by 21 cm?
Solution:

Question 35.
The following table gives the monthly consumption of electricity of 100 families:

Find the median of the above data.
Solution:

Monthly Consumption	Number of families(f)	Cumulative frequency (C.f)
130-140	5	5
140-150	9	14
150-160	17	31
160-170	28	59
170-180	24	83
180-190	10	93
190-200	7	100

Section – E(12 Marks)

Question 36.
Sonu is studying in X standard. He is making a brooch and understanding areas related to circles. A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors.

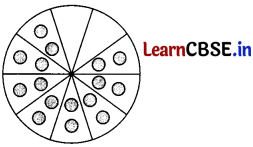
Few questions came in his mind while making the brooch. Give answers to his questions.

(i) Find the area of circle.
Answer:
∴ Area of circle = πr²
= π \(\)
= \(\)
= 11 × 5 × \(\frac{35}{2}\)
= \(\frac{1925}{2}\)
= 962.5 mm²

(ii) Find the measure of angle of each sector.
Answer:
Since total circle is divided into 10 sectors
∴ Angle of each sector = \(\frac{360^{\circ}}{10}\) = 36°

(iii) Find the area of each sector of the brooch.
Answer:
(iii) Area of each sector of the brooch = \(\frac{\theta}{360^{\circ}}\) × πr²
= \(\frac{36^{\circ}}{360^{\circ}} \times \frac{22}{7}\left(\frac{35}{2}\right)^2\)
[∵ r = \(\frac{d}{2}\)
= \(\frac{35}{2}\) mm]
= \(\frac{1}{10} \times \frac{22}{1} \times \frac{5}{2} \times \frac{35}{2}\)
= \(\frac{11 \times 35}{2 \times 2}\)
= \(\frac{385}{4}\) mm²

Or

Find the total length of the silver wire.
Answer:
Circumference of circle = πd
= \(\frac{22}{7}\) × 35
= 110 mm
Total length of the silver wire = πd + 5d
= 110 + 5 × 35
= 285 mm

Question 37.
An electrician has to repair an electric fault on the pole of height 5 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work (see figure).

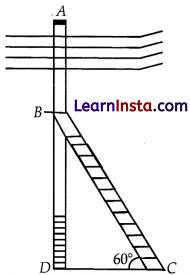
(i) What is the length of BD?
(ii) What should be the length of ladder, when inclined at an angle of 60° to the horizontal?
(iii) How far from the foot of the pole should he place the foot of the ladder?
Solution:
(i) From figure, the electrician is required to reach at the point B on the pole AD.

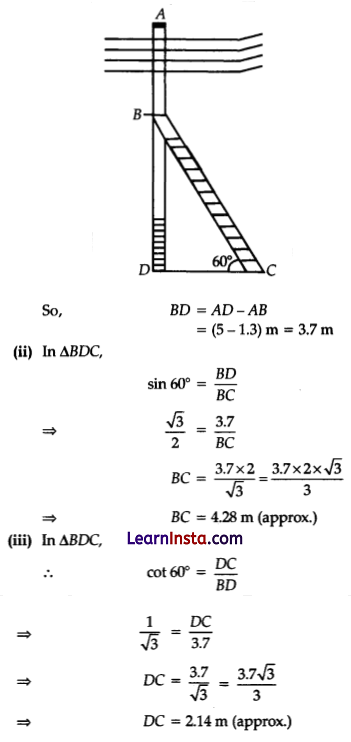
OR

If the horizontal angle is changed to 30°, then what should be the length of the ladder?
Solution:
In ΔBDC,
∴ sin 30° = \(\frac{B D}{B C}\)
⇒ \(\frac{1}{2}\) = \(\frac{3.7}{B C}[latex]
⇒ BC = 3.7 × 2 = 7.4 m

Question 38.
In order to conduct Sports Day activities in your School, lines have been drawn with chalk powder at a distance of 1 m each, in a rectangular shaped ground ABCD, 100 flowerpots have been placed at a distance of 1 m from each other along AD, as shown in given figure below. Niharika runs [latex]1 / 4^{\text {th }}\) the distance AD on the 2^th line and posts a green (G) flag. Preet runs \(1 / 5^{\text {th }}\) distance AD on the eighth line and posts a red (R) flag.

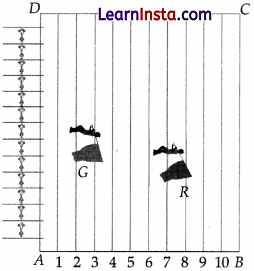
Answer the following questions:
(i) Find the position of green flag.
(ii) Find the position of red flag.
(iii) What is the distance between both the flags?
Solution:
(i) From the given figure, abscissa = 2 and ordinate = \(\frac{1}{4}^{\text {th }}\) of 100
= \(\frac{1}{4}\) × 100 = 25
So, required point = G(2, 25)
(ii) From the given figure, abscissa = 8 and ordinate = \(\frac{1}{5}^{\text {th }}\) of 100
= \(\frac{1}{5}\) × 100 = 20
So, required point = R (8, 20)
(iii) Position of Green flag = (2, 25)
Position of Red flag = (8, 20)
Distance between both the flags
\(\begin{aligned}
\left|\sqrt{(8-2)^2+(20-25)^2}\right| & =\left|\sqrt{6^2+(-5)^2}\right| \\
& =\sqrt{36+25} \\
& =\sqrt{61} \text { units }
\end{aligned}\)

OR

If Rashmi has to post a blue flag exactly half way between the line segment joining the flags, where should she post her flag?
Solution:
Position of blue flag
Mid-point of line segment joining the green and red flags
= \(\left(\frac{2+8}{2}, \frac{25+20}{2}\right)\) = (5, 22.5)