CBSE Sample Papers for Class 10 Maths Basic Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 3 with Solutions

Maximum Marks: 80
Time Allowed: 3 hours

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answers-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answers-IT (SA-II) type questions carrying 3 marks each
5. Section D has 4 Long Answers (LA) type questions carrying 5 marks each.
6. Section E has 3 source based/case based/passage based integrated units of assessment (4 marks each) with sub¬ parts of the values of 1,1 and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Qs of 5 marks has been given provided. An internal choice has been provided in 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7, wherever required if not stated.

Section – A (20 Marks)

Question 1.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is:
(A) 10
(B) 100
(B) 504
(D) 2520
Solution:
(D) 2520
Explanation: Required number
= LCM (1, 2, 3, 4, 5, 6, 8, 9, 10)
= 1 × 2 × 2 × 2 × 3 × 3 × 5 × 7 = 2,520

Question 2.
1245 is a factor of the numbers p and q.
Which of the following will always have 1245 as a factor?
(i) p + q (ii) p × q (iii) p ÷ 4
(A) only (ii)
(B) only (i) and (ii)
(C) only (ii) and (iii)
(D) all – (i), (ii) and (iii)
Solution:
(B) only (i) and (ii)
Explanation: Given, 1245 is a factor of two numbers
p and q.
∴ p = 1245 A and q = 1245 B
Now, p + q = 1245 A + 1245 B = 1245 (A + B)
Hence, p + q have a factor 1245 always.
Now, p × q = 1245 A ×1245 B = (1245)² AB
Hence, p × q have a factor 1245 always.

Question 3.
In which quadrant does the point (-1, -2) lie? 1
(a) I
(b) II
(c) III
(d) IV
Answer:
(c) III
Explanation: Third quadrant since, both ‘x’ and ‘y’ are negative.

Question 4.
What about the number of solutions if the given system of equations is inconsistent?
(A) One solution
(B) Infinite or many solutions
(C) No solution
(D) None of these
Solution:
(C) No solution
Explanation: As we know that,
An inconsistent system of equations, represent a pair of parallel lines that never intersects each other. So, It has No solution.

Question 5.
Which of the following is not a quadratic equation?
(A) 2(x- 1)² = 4x² – 2x + 1
(B) 2x – x² = x² + 5
(C) (√2x + √3 )² + x² = 3x² – 5x
(D) (x² + 2x)² = x⁴ + 3 + 4x³
Solution:
(C) (√2x + √3 )² + x² = 3x² – 5x
Explanation:
(√2x)² + (√3)² + 2 × √2x × √3 + x² = 3x² – 5x
2x² + 3 + 2√6x + x² = 3x² – 5x
3x² + 2√6x + 3 = 3x² – 5x
x(5 + 2√6) + 3 = 0

Question 6.
If the pair of lines are coincident, then we say that pair of lines is consistent and it has a
(a) unique solution
(b) no solution
(c) infinite solutions
(d) None of the above
Answer:
(c) infinite solutions

If the pair of lines are coincident, then it has an infinite number of solutions and hence, is consistent.

Question 7.

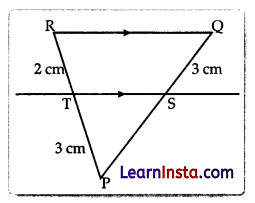
In the above figure, ST is parallel to QR. What is the length of SP?
(A) 2cm
(B) 3cm
(C) 4cm
(D) 45cm
Solution:
(D) 45cm
Explanation: As it is given that ST || QR,
According to BPT, If a line is drawn parallel to one side of the triangle intersecting other two sides at two distinct points. Then, other two sides are divided in the same ratio.
\(\begin{aligned}
\frac{R T}{T P} & =\frac{Q S}{S P} \\
\frac{2}{3} & =\frac{3}{S P} \\
S P & =\frac{3 \times 3}{2}=\frac{9}{2}=4.5 \mathrm{~cm}
\end{aligned}\)

Question 8.

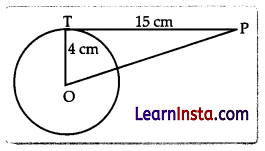
In the above diagram, OT = 4 cm, is the radius of the circle with centre O and a tangent PT is drawn from a point P such that PT = 15 cm.
The length of OP to correct two decimal places is :
(A) 11.00cm
(B) 10.44cm
(C) 15.52cm
(D) 19.00cm
Solution:
(C) 15.52cm
Explanation:

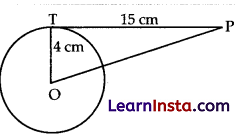
OT is the radius of the circle and TP is the tangent.
According to the property, Radius is perpendicular to the tangent.
AOTP is a right angled triangle.
According to the Pythagoras theorem, OP² = FT² + OT²
= 152 + 42
= 225 + 16
= 241
OP = √241
= 15.52 cm

Question 9.
tan² θ sin² θ is: 1
(a) tan² θ – sin² θ
(b) tan² θ + sin² θ
(c) \(\frac{\tan ^2 \theta}{\sin ^2 \theta}\)
(d) sin² θ cot² θ
Answer:
(a) tan² θ – sin² θ
Explanation:
tan² θ – sin² θ = \(\frac{\sin ^2 \theta \sin ^2 \theta}{\cos ^2 \theta}\)
sin² θ(\(\frac{1-\cos ^2 \theta}{\cos ^2 \theta}\))
= \(\frac{\sin ^2 \theta}{\cos ^2 \theta}\) – sin² θ
= tan² θ – sin² θ

Question 10.
Given that sin α = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\), then the value of (α + β) is
(A) 0°
(B) 30°
(C) 60°
(D) 90°
Solution:
(D) 90°

Question 11.
The value of 6, for which sin 2θ = 1/2; 0° < 6 < 90° is
(A) 15°
(B) 30°
(C) 45°
(D) 60°
Solution:
(A) 15°
Explanation: sin 2θ = 1/2   …(i)
Also, sin 30° = 1/2   …(ii)
On comparing both (i) and (ii), we get
2θ = 30°
θ = 15°

Question 12.
The centroid of an ∆ABC, whose vertices are A (1, 2), B (- 1, 3) and C (3, – 1) are
(a) (\(\frac{3}{2}\), 2)
(b) (3, 4)
(c) (1, \(\frac{4}{3}\))
(d) None of these
Answer:
(c) (1, \(\frac{4}{3}\))

The centroid of an ∆ABC having vertices A (1, 2), B (- 1, 3) and C (3, – 1) is
G\(\left(\frac{1-1+3}{3}, \frac{2+3-1}{3}\right)\) or G(1, \(\frac{4}{3}\))

Question 13.
The minute hand of a clock is 84 cm long. The distance covered by the tip of minute hand from 10:10 am to 10:25 am is
(A) 44cm
(B) 88cm
(C) 132cm
(D) 176cm
Solution:
(C) 132cm
Explanation: Length of minute hand = Radius of the quadrant/sector so formed = 84 cm. In 1 minute, minute hand makes an angle of 6°.
Therefore, in 15 minutes it makes an angle of 15 × 6° = 90°
Distance covered by the tip of the minute hand = Length of arc
\(\begin{aligned}
& =\frac{\theta}{360^{\circ}} \times 2 \pi r \\
& =\frac{90^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7} \times 84
\end{aligned}\) = 132 cm.

Question 14.
If the perimeter of a circle is equal to that of a square, then the ratio of their areas
(A) 22:7
(B) 14:11
(C) 7:22
(D) 11:14
Solution:
(B) 14:11
Explanation: Let the radius of circle be ‘r’ and side of square be ‘a’.
According to given question,
Perimeter of circle = Perimeter of square 2πr = 4a
∴ a = \(\frac{\pi r}{2}\)   …(i)
So, \(\frac{\text { Area of circle }}{\text { Area of square }}=\frac{\pi r^2}{\left(\frac{\pi r}{2}\right)^2}\)  [from equation (i)]
Solving equation (i), we get result as 14/11.

Question 15.
The roots of the quadratic equation 2x² – 3x – 5 = 0 are: 1
(a) both equal
(b) opposite integers
(c) rational and unequal
(d) not real
Answer:
(c) rational and unequal
Explanation: We have,
2x² – 3x – 5 =0
Here, a = 2, b = – 3 and c = – 5.
∴ D = b² – 4ac
= (- 3)² – 4(2)(- 5)
= 9 + 40
= 49 > 0
and 49 is a perfect square also.
Thus, the given equation has rational and unequal roots.

Question 16.
Look at the numbers shown below.
(i) 0.5
(ii) 0.00001
(iii) 1/2
(iv) 1
(v) 1.00001
(vi) 99%
Which of the above numbers represent probabilities of events?
(A) only (i) and (iii)
(B) only (i), (ii), (iii) and (iv)
(C) only (ii), (iii), (iv) and (v)
(D) only (ii), (iii), (iv) and (vi)
Solution:
(D) only (ii), (iii), (iv) and (vi)
Explanation: Since, we know that the probability can neither be negative and nor be greater than one.
So, -0.5 and 1.00001 can not represent probabilities of events.
Hence, only (ii), (iii), (iv) and (vi) represent probabilities of events.

Question 17.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that 1/8 space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is
(A) 142296
(B) 142396
(C) 142496
(D) 142596
Solution:
(A) 142296
Explanation: Let the spherical marble has radius r.
Diameter of the marble= 0.5 cm
⇒ r = 0.5/2 cm = 0.25 cm
Length of side of cube / = 22 cm
Let n marbles can fill the cube.
∴ Volume of n marbles = (1 – 1/8) part of volume of cube

Question 18.
The pair of equations 3x + 2y + 7 = 0 and 6x + 4y + 14 = 0 has
(a) unique solution
(b) exactly two solutions
(c) infinitely many solutions
(d) no solution
Answer:
(c) infinitely many solutions

Given, 3x + 2y + 7 = 0
and 6x + 4y +14 = 0
Here, \(\frac{a_1}{a_2}=\frac{3}{6}=\frac{1}{2}\)
\(\frac{b_1}{b_2}=\frac{2}{4}=\frac{1}{2}\)
and \(\frac{c_1}{c_2}=\frac{7}{14}=\frac{1}{2}\)
Hence, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}=\frac{1}{2}\)
So, the lines representing the given pair of linear equations will coincide, therefore there are infinitely many solutions.

Question 19.
Assertion (A): AABC with vertices A(-2, 0), B(2, 0) and C(0, 2) is similar to ΔDEF with vertices D(-4, 0), E(4, 0) and F(0, 4).
Reason (R): A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) Jies outside the circle.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A)is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).

Here, we see that sides of AABC and AFDE are proportional.
Therefore, by SSS similarity rule, both the triangles are similar.
∴ Assertion is correct.
In case of reason:
Point Q (6, 8) will lie outside the circle if its distance from the centre of circle is greater than the radius of the circle.
Distance between centre O (0, 0) and P (5, 0)

Here, OQ > OP (radius of circle) therefore, the point Q(6, 8) lies outside the circle.

Question 20.
Assertion (A): If HCF (336, 54) = 9, then LCM (336, 54) = 2016.
Reason (R): The sum of exponents of prime factors in the prime factorisation of 196 is 4.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
Explanation: Let us consider the assertion,
∴ HCF × LCM = Product of numbers
∴ 9 × LCM = 336 × 54
⇒ LCM = \(\frac{336 \times 54}{9}\) = 2016
Thus, the assertion is correct.
Now, let us consider the reason:
Prime factors of 196 = 2² × 7²
∴ The sum of exponents of prime factors = 2 + 2 = 4
So, the reason is correct. Thus, assertion is correct and reason is also correct.

Section – B(10 Marks)

Question 21.
Show that 3 + √5 is an irrational number, assume that √5 is an irrational number. 2
Answer:
If possible, let us assume that 3 + √5 is a rational number. So, there exist positive integers a and b such that, 3 + √5 = \(\frac{a}{b}\), where a and b are integers having no common factor other than 1 and b ≠ 0.
⇒ √5 = \(\frac{a}{b}\) – 3
√5 = \(\frac{a-3 b}{b}\)
Since, \(\frac{a-3 b}{b}\) is a rational number, √5 is a rational number which is a contradiction to the fact that “ √5 is irrational”.
Hence, 3 + √5 is irrational.

Question 22.
In given figure, O is the centre of the circle and LN is a diameter. If PQ is a tangent to the circle at K and ∠KLN = 30°, find ∠PKL.

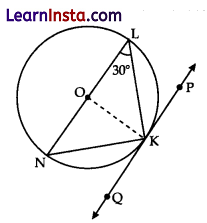
Solution:

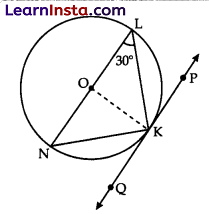
Here, OK = OL
∠OKL = ∠OLK = 30°
[Opposite angles of equal sides]
Since ∠OKP = 90° [Tangents]
∠PKL =90° – 30° = 60°

OR

In the given figure, OA × OB = OC × OD, show that ∠A = ∠C and ∠B = ∠D.

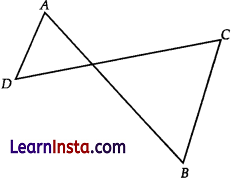
Solution:

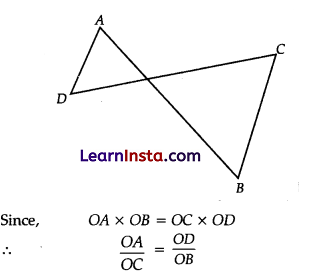
Also, ∠AOD = ∠COB (vertically opposite angles)
ΔAOD ∼ ΔCOB (SAS similarity)
∠A = ∠C and ∠B = ∠D. (Corresponding angles of similar triangles)

Question 23.
In figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°, find ∠TRQ.

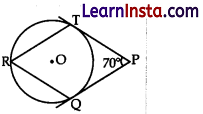
Solution:

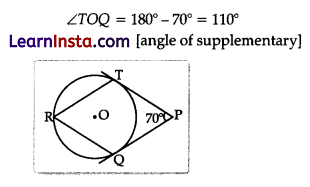
Then ∠TRQ = 1/2 ∠TOQ [angle at the circumference of the circle by same arc]
= 1/2 ×110° = 55°

Question 24.
If α and β are the zeroes of quadratic polynomial p(y) = 3y² + 5y + 2, then find the value of α + αβ + β.
Answer:
Given, polynomial is p(y) = 3y² + 5y + 2
Now, sum of zeroes, α + β = – \(\frac{\text { Coefficient of } y}{\text { Coefficient of } y^2}\)
= – \(\frac{5}{3}\)
and product of zeroes, = Constant term / Coefficient of $y^2$
= \(\frac{2}{3}\)
Now, α + αβ + β = (α + β) + αβ
= \(-\frac{5}{3}+\frac{2}{3}\)
= \(-\frac{3}{3}\) = -1

Question 25.
A piece of wire 22 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle. [use π = \(\frac{22}{7}\)]
Solution:

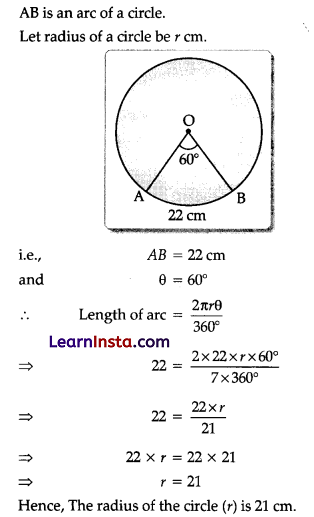
OR

The volume of a right circular cylinder with its height equal to the radius is 25 1/7 cm³, Find the height of the cylinder. [use π = \(\frac{22}{7}\)]
Solution:

Section – C(18 Marks)

Question 26.
Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of the two given numbers.
Solution:
Let a = 404 and b = 96
Expressing the number as a product of prime number
404 = 2 × 2 × 101
96 = 2 × 2 × 2 × 2 × 2 × 3
LCM of 404 and 96 is 2 × 2 × 2 × 2 × 2 × 101 × 3 = 9696
HCF 404 and 96 is 2 × 2 = 4
Now, HCF * LCM = 4 × 9696 = 38784
product of two given numbers 404 × 96 = 38784
Hence HCM × LCM = product of two given numbers.

Question 27.
The figure drawn on the graph paper shows a ΔABC with vertices A (-4, 1), B (-4, 6), and C (8, 1).

(A) Show that the Length of BC is 13.
(B) Find AB. 3
Answer:

Question 28.
Solve for x and y:
\(\frac{6}{x-1}-\frac{3}{y-2}=1 and \frac{5}{x-1}+\frac{1}{y-2}=2, where x \neq 1 and y \neq 2\)
Solution:

y = 5
Hence, x = 4 and y = 5

OR

Which term of the AP 20, 19 \(\frac{1}{4}\), 18 \(\frac{1}{2}\), 17 \(\frac{3}{4}\) sen is the first negative term?
Solution:

Question 29.
In the given figure, if AABC ~ DEF and their sides of the given figure lengths (in cm) are marked along them, then find the lengths of sides of each triangle.

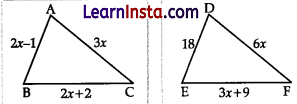
Solution:
Given, ΔABC ∼ ΔDEF
Then according to question, \(\frac{A B}{D E}=\frac{B C}{E F}\)
[Ratio of corresponding sides of two similar triangles are equal]
⇒ \(\frac{2 x-1}{18}=\frac{2 x+2}{3 x+9}\)
⇒ (2x – 1)(3x + 9) = 18(2x + 2)
⇒ (2x – 1)(x + 3) = 6(2x + 2)
⇒ 2x² – x + 6x – 3 = 12x + 12
⇒ 2x² + 5x – 12x – 15 =0
⇒ 2x² – 7x – 15 = 0
⇒ 2x² – 10x + 3x – 15 =0
⇒ 2x(x – 5) + 3(x – 5) = 0
⇒ (x – 5)(2x + 3) =0
Either x = 5 or x = -3/2 , which is not possible
So, x = 5
Then in ΔABC, we have
AB = 2x – 1 = 2 × 5 – 1 = 9
BC = 2x + 2 = 2 × 5 + 2 = 12
AC = 3x = 3 × 5 = 15
and in ADEF, we have
DE = 18
EF = 3x + 9 = 3 × 5 + 9 = 24
DE = 6x = 6 × 5 = 30

Question 30.
If tan θ = \(\frac{12}{5}\), then find the value of \(\frac{1+\sin \theta}{1-\sin \theta}\).
Answer:
We have tan θ = \(\frac{12}{5}\)
∴ sec θ = \(\)
[∵ sec² A = 1 + tan² A]
= \(\sqrt{1+\tan ^2 \theta}\)
= \(\sqrt{1+\left(\frac{12}{5}\right)^2}\)
= \(\sqrt{\frac{169}{25}}=\frac{13}{5}\)
∴ \(\frac{1+\sin \theta}{1-\sin \theta}=\frac{\sec \theta+\tan \theta}{\sec \theta-\tan \theta}\)
[divide numerator and denominator by cos θ]
= \(\frac{\frac{13}{5}+\frac{12}{5}}{\frac{13}{5}-\frac{12}{5}}\)
= 25

Or

If sin (A + B) = 1 and cos (A – B) = \(\frac{\sqrt{3}}{2}\), 0° < A + B ≤ 90°, A > B, then find the values of A and B.
Answer:
We have, sin (A + B) = 1
sin (A + B) = sin 90°
⇒ A + B = 90° …………(i)
and cos (A – B) = \(\frac{\sqrt{3}}{2}\)
cos (A – B) = cos 30°
⇒ A – B = 30° …………(ii)
On adding Eqs. (i) and (ii), we get
(A + B) + (A – B) = 90° + 30°
⇒ 2A = 120°
⇒ A = 60°
On putting A = 60° in Eq. (i), we get
60° + B = 90°
⇒ B = 30°
Hence. A = 60° and B = 30°.

Question 31.
A box contains cards, number 1 to 90. A card is drawn at random from the box. Find the probability that the selected card bears a :
(i) Two digit number
(ii) Perfect square number
Solution:
No. of all possible outcomes = 90
(i) No. of cards having 2 digit number = 90 – 9 = 81
∴ No. of favourable outcomes = 81
P(selected card bears two digit number) = \(\frac{\text { No. of favourable outcomes }}{\text { No. of all possible outcomes }}=\frac{81}{90}=\frac{9}{10}\)
(ii) Perfect square numbers from 1 to 90 are 1, 4, 9, 16, 25, 36, 49, 64, 81
∴ No. of favourable outcomes = 9
P(Selected card bears perfect square numbers) = \(\frac{9}{90}=\frac{1}{10}\)

Section – D(20 Marks)

Question 32.
Ina painting competition of a school a child made Indian national flag whose perimeter was 50 cm. Its area will be decreased by 6 square cm, if its length is decreased by 3 cm and breadth is increased by 2 cm. Find the dimensions of the flag.
Also find the correct area of the flag.
Solution:
Let length of flag = x cm
Let breadth of flag = y cm ’
Perimeter of rectangular flag = 2 (L + B)
50 = 2(x + y)
Or, x + y = 25  …(i)
Area of rectangular flag = Length x Breadth = (x)(y) = (xy)
According to the question, (x – 3)(y + 2) = (xy – 6)
⇒ xy + 2x – 3y – 6 = xy – 6
⇒ 2x – 3y = 0  …(ii)
Take (i), x + y = 25
Or, y = 25 – x
Put value of y in (ii),
2x – 3 (25 – x) =0
Or, 2x – 75 + 3x =0
Or, x = 15
So, y = 25 – x = 25 – 15 = 10
Therefore, Length of flag = 15 cm & Breadth of flag = 10 cm
Area of the flag = length x breadth = 15 × 10 = 150 sq. Units

OR

(a) A two digit number is obtained by either multiplying the sum of digits by 8 and then subtracting 5 or by multiplying the difference of digits by 16 and adding 3. Find the number.
(b) Solve: 4x + 5y = 0 and 2x – 3y = 0
Solution:
Let the number be xy
x is at tenth’s place and y is at one’s place
Therefore, the number is 10x + y
Ist case
(x + y) × 8 – 5 = 10x + y
Or, 8x + 8y – 5 = 10x + y
Or, 2x – 7y = -5   …(i)
IInd case,
(x- y) × 16 + 3 = 10x + y
Or, 16x – 16y + 3 = 10x + y
Or, 6x – 17y = -3
Multiply equation (i) by 3 and subtract (ii) from (i),
4y – 12 = 0
Or, y = 12/4 = 3
Put y = 3 in (i).
⇒ 2(x) – 7 × 3 = -5
⇒ 2x – 21 = -5
⇒ 2x = -5 + 21
⇒ x = 16/3 = 8
Therefore, the number is 83.
(b) 4x + 5y = 0  …(i)
2x – 3y =0 …(ii)
Multiply equation (i) by 3 and equation (ii) by 5 and then add
12x + 15y = 0
10x – 15y = 0
Add, we get 22x = 0
x = 0
Put value of x in (i), we get y = 0.

Question 33.
A vessel contains mixture of 24 l milk and 6 l water and a second vessel contains a mixture of 15 l milk and 10 l water. How much mixture of milk and water should be taken from the first and the second vessel separately and kept in a third vessel so that the third vessel may contain a mixture of 25 l milk and 10 l water?
OR
Solve algebraically: 4x + 3y = 14 and 3x – 4y = 23. 5
Answer:
Let x L of mixture be taken from 1^st vessel and y l of the mixture be taken from 2^nd vessel and kept in 3^rd vessel so that (x + y) l of the mixture in third vessel may contains 25 l of milk and of 10 l of water.
A mixture of x l from 1^st vessel contains \(\frac{24}{30}\) x l = \(\frac{4}{5}\) x l of milk and \(\frac{x}{5}\) l of water. And a mixture of y l from 2^nd vessel contains \(\frac{3 y}{5}\) of milk and \(\frac{2 y}{5}\) l of water.
∴ \(\frac{4}{5}\)x + \(\frac{3}{5}\)y = 25
⇒ 4x + 3y = 125 ………. (i)
and \(\frac{x}{5}\) + \(\frac{2}{5}\)y = 10
⇒ x + 2y = 50 ………… (ii)
Multiplying (ii) by 4 and then subtracting (i) from it, we get
4x + 8y – 4x – 3y = 200 – 125
⇒ 5y = 75
⇒ y = 15
From (ii),
x + 2 × 15 = 50
⇒ x = 50 – 30
⇒ x = 20
OR
Given, 4x + 3y = 14 ……….. (i)
and 3x – 4y = 23 …………. (ii)
Adding (i) and (ii), we get
7x – y = 37
∴ y = 7x – 37 ………… (iii)
Substituting the value of y in equation (i), we get
4x + 3 (7x – 37) = 14
⇒ 4x + 21x – 111 = 14
⇒ 25x = 125
⇒ x = 5
Putting x = 5 in eq. (iii), we get
y = 7 (5) – 37
= 35 – 37 = – 2
∴ The solution is x = 5 and y = – 2.

Question 34.
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm³ of iron has approximately 8 gm mass. (Use π = 3.14)
Solution:

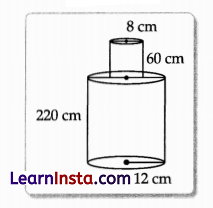
To find mass of pole, we need to find volume of pole.
Volume of pole = Volume of small cylinder + Volume of large cylinder.
Now, for small cylinder,
Radius, r = 8 cm
Height,h₁ = 60 cm
Volume of small cylinder
= π r²h₁
= 3.14 x (8)² x 60
= 3.14 x 64 x 60
= 12057.6 cm3
Volume of large cylinder,
Height = h₂ = 220 cm³
Radius = R = \(\frac{\text { diameter }}{2}\)
= \(\frac{24}{2}\) = 12
Volume of large cylinder = πR²h₂
= 3.14 × (12)² × 220
= 3.14 × 144 × 220
= 99475.2 cm³
Now, Volume of pole = Volume of small cylinder + Volume of large cylinder
= 12057.6 + 99475.2
= 111532.8 cm³
Since,1 cm³ of iron has 8 gm mass
So, given volume of iron has mass
= 111532.8 x 8 gm
= 892262.4 gm
= \(=\frac{892262.4}{1000} \mathrm{~kg}\)
= 892.2624 kg
= 892.262 kg

OR

Two circular beads of different sizes are joined together such that the distance between their centres is 14 cm. The ‘sum of their areas is 130 π cm². Find the radius of each bead.
Solution:

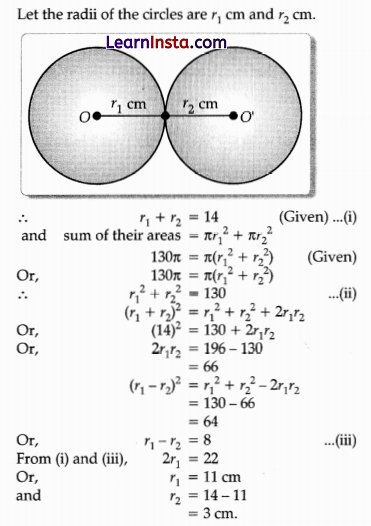
Question 35.
If the median of the following frequency distribution is 32.5. Find the values of f1 and f2.

Solution:

Class	Frequency(f)	Cumulative frequency (c.f)
0-10	f1	f1
10-20	5	f1 + 5
20-30	9	f1 + 14
30-40	12	f1 + 26
40-50	f2	f1 + f2 +  26
50-60	3	f1 + f2 + 29
60-70	2	f1+ f2 + 31
	N = Σf = 40

 

Section – E(12 Marks)

Question 36.
People of village Road want to construct a road nearest to a circular village Rampur. The road cannot pass through the village. But the people want the road should be at the shortest distance from the centre of the village. Suppose, the road start from point O, which is outside the circular village and touch the boundary of the circular village at point A such that OA = 20 cm and also, the straight distance of the point O from the centre C of the village is 25 cm.

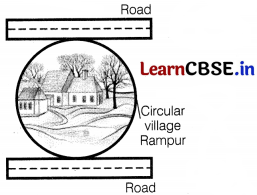
Based on above information, answer the following questions.
(i) If a point is inside the circle, how many tangents can be drawn from that point?
(ii) If two circles are externally and they do not touch, then find the number of common tangents.
(iii) Find the shortest distance of the road from the centre of the village.
Answer:
(i) If a point is inside the circle, then no tangent can be drawn.

(ii)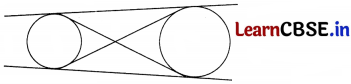

Four common tangents can be drawn, when the two circles does not touch externally.

(iii) Given, OA =20 cm and OC =25 cm

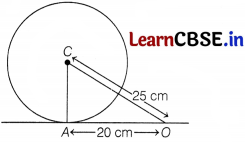
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ In ∆OAC,
AC ⊥ OA
In right-angled ∆OAC,
OC² = OA² + AC²
[by Pythagoras theorem]
⇒ (25)² = (20)² + AC²
625 = 400 + AC²
⇒ AC² = 225
⇒ AC = 15 cm

Or

If DE and DF are tangents from the external point D to the circular village. If DE ⊥ DF, then find the length of DE.
Answer:
∵ DE ⊥ DF,
∠EDF = 90°
and we know CE ⊥ ED and CF ⊥ FD
[∵ tangent is perpendicular to the radius through the point of contact]
Also, CF = CE

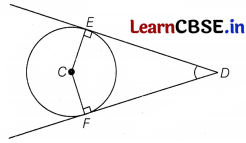
∴ FCED is a square.
⇒ CE = CF = FD = DE
∴ DE = 15 cm
[∵ radius = 15 cm]

Question 37.
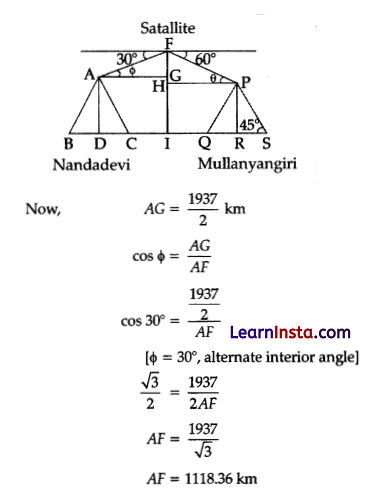
A satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka, them being Nanda Devi (height 7,816 m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite, to the top of Nanda Devi and Mullayanagiri are 30° and 60° respectively. If the distance between the peaks of two mountains is 1937 km and the satellite is vertically above the midpoint of the distance between the two mountains.

What is the distance of the satellite from the top of Nanda Devi.
Solution:

OR

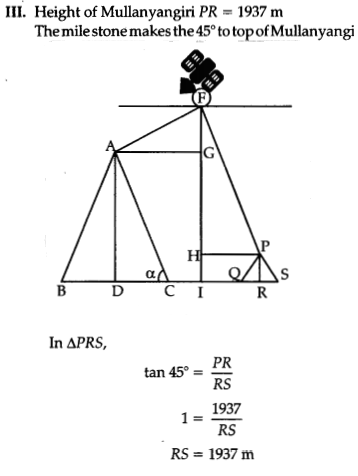
I. What is the distance of the satellite from the top of Mullayanagiri.
II. Whatis the angle of elevation if a man is standing at a distance of 7816 m from Nanda Devi?
III. If a mile stone very far away from, makes 45° to the top of Mullanyangiri mountain. So, find the distance of this mile stone from the mountain.

Question 38.
A small scale industry produces a certain boxes of candles in a day. Number of boxes prepared by each worked on a particular day was 2 more than thrice the number of workers working in the industry. The number of boxes produced in a particular day was 85.

I. If the number of workers working in the industry is x. What was the number of boxes of candles prepared by each worker on that particular day?
II. Write the quadratic equation for the given case.
Ill. Find the number of workers working in the industry.
Solution:
I. Let the workers are x, Number of boxes prepared by the each workers = 2 + 3x
II. x(2 + 3x) = 85
⇒ 2x + 3x² = 85
⇒ 3x² + 2x – 85 = 0
III. x(2 + 3x) = 85
2x + 3x² = 85
3x² + 2x – 85 =0
3x² + 17x – 15x – 85 =0
x(3x + 17) – 5 (3x + 17) =0
(3x +17) (x – 5) =0
x = -17/3 or x = 5
Number of workers cannot be negative; therefore x = 5

OR

How many boxes will be prepared when number of workers are increased by 2.
Solution:
Number of workers = x
Number of workers when increased by 2 = x + 2
∴ Number of boxes prepared by the workers
(x + 2) = (x + 2) [2 + 3 (x + 2)]
= 7 [2 + 3 × 7] (∴ x = 5)
= 7 × 23
= 161