Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 10 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Basic Set 10 with Solutions
Time: 3 Hours
Maximum Marks: 80
General Instructions:
1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answers-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answers-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answers (LA) type questions carrying 5 marks each.
6. Section E has 3 source-based/case-based/passage-based integrated units of assessment (4 marks each) with sub-parts of the values of 1, 1, and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks, and 2 Qs of 5 marks has been given provided. An internal choice has been provided in 2-mark questions of Section E.
8. Draw neat figures wherever required, Take. x = 2, wherever required if not stated.
Section-A(20 Marks)
Question 1.
√5 + √2 is
(A) rational number
(B) prime number
(C) irrational number
(D) composite number
Solution:
(C) irrational number
Explanation: √5 is an irrational number and 2 is also an irrational number and addition of two irrational number is also irrational.
∴ (√5 + √2) is irrational.
Question 2.
(HCF × LCM) for the numbers 70 and 40 is
(A) 10
(B) 280
(C) 2800
(D) 70
Solution:
(C) 2800
Explanation: Given numbers are 70 and 40
We know that, HCF × LCM = Product of numbers
So, HCF × LCM = 70 × 40 = 2800
Question 3.
Which term of the A.P., 21, 42, 63, 84,… is 210?
(A) 9th
(B) 10th
(C) 11th
(D) 12th
Solution:
(B) 10th
Explanation : In the given A.P., a = 21, d = 42 – 21 = 21, and tn = 210
Thus, tn = a + (n – 1)d
⇒ 210 = 21 + (n – 1)21
⇒ 189 = (n – 1)21
⇒ n = 10
Question 4.
What is the value of q if p/2 + 3q = 6 and 2p – 2q = 10?
(A) 1
(B) 4
(C) 6
(D) 16
Solution:
(A) 1
Explanation: On solving the pair of linear equations p/2 + 3q = 6 and 2p − 2q = 10
On simplifying we have, p + 6q = 12 and p – q = 5
p + 6q = 12
p – q = 5
– + –
7q = 7 q = 1 and p = 6
![]()
Question 5.
Which of the following is a quadratic equation?
(A) x2 + 2x + 1 = (4 – x)2
(B) – 2x2 = (5 – x)(2x – 2)
(C) 7x2 + 3 = 7x2 + 3x
(D) x3 – x2 = (x – 1)3
Solution:
(D) x3 – x2 = (x – 1)3
Explanation: Consider option (D),
x3 – x2 = (x – 1)3
x3 – x2 = x3 – 1 – 3x(x – 1)
x3 – x2 = x3 – 1 – 3x2 + 3x
2x2 – 3x + 1 = 0
It is of the form ax2 + bx + c.
Question 6.
Distance of the point (6, 5) from the y-axis is
(A) 6 units
(B) 5 units
(C) √61 units
(D) 0 unit
Solution:
(A) 6 units
Explanation: Distance of the point (6, 5) from the y-axis = 6 units
Question 7.
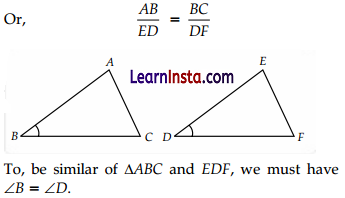
If in triangles ΔABC and ΔDEF, \(\frac{A B}{D E}=\frac{B C}{F D}\), then they will be similar, when
(A) ∠B = ∠E
(B) ∠A =∠D
(C) ∠B = ∠D
(D) ∠A = ∠F
Solution:
(C) ∠B = ∠D
In ΔABC and ΔDEF, \(\frac{A B}{D E}=\frac{B C}{F D}\)
Question 8.
In the figure given below, two line segments AC and BD intersect each other at the point P such that PA = 6cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB =50° and ∠CDP = 30°. Then, ∠PBA is equal to
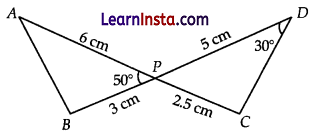
(A) 50°
(B) 30°
(C) 60°
(D) 100°
Solution:
(D) 100°
Explanation: In the given figure, \(\frac{P A}{P B}=\frac{6}{3}\) = 2
and \(\frac{P D}{P C}=\frac{5}{2.5}\) = 2
Thus, \(\frac{P A}{P B}=\frac{P D}{P C}\) and ∠APB = ∠DPC
By SAS similarity, we get ∠APB ~ ∠DPC. Hence, ∠PBA = 100°
Question 9.
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 115°, then ∠PTQ is equal to
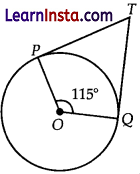
(A) 65°
(B) 75°
(C) 85°
(D) 95°
Solution:
(A) 65°
Explanation:
∠PTQ + ∠PQO = 180°
∠PTQ + 115° = 180°
∠PTQ = 180° – 115° = 65°
Question 10.
If ΔABC is right-angled at C, then the value of cos (A+B) is :
(A) 0
(B) 1
(C) 1/2
(D) √3/2
Solution:
(A) 0
Explanation: In ΔABC,
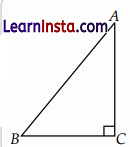
sum of three angles = 180°
i.e., ∠A + ∠B+ ∠C = 180°
∠C = °90 [Given]
∠A + ∠B + ∠C = 180°
⇒ A + B = 90°
∴ cos (A + B) = cos 90° = 0
Question 11.
In figure, a tower AB is 20 m high and BC, its shadow on the ground, is 20 √3 m long. Find the Sun’s altitude.
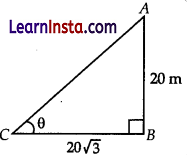
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Solution:
(A) 30°

Question 12.
The value of cos 1° cos 2° cos 3° cos 4° ___________ cos 90° is
(a) 1
(B) 0
(C) -1
(D) 2
Solution:
Option (B) is correct.
Explanation : (cos 1°) × (cos 2°) × (cos 3°) × (cos 4°) × … × (cos 90°)
= (cos 1°) × (cos 2°) × (cos 3°) × (cos 4°) × … × (0)
[∴ cos 90° = 0] = 0
![]()
Question 13.
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then :
(A) R1 + R2 = R
(B) R1 + R2 >R
(C) R1 + R2 <R
(D) Nothing definite can be said about the relation among R1, R2 and R
Solution:
(A) R1 + R2 = R
Explanation: According to question, Circumference of circle = Circumference of first circle + Circumference of second circle
2πR = 2πR1 + 2πR2
R1 + R2 = R
Question 14.
The Hour hand of a clock is 21 cm long. The distance covered by the tip of Hour hand in one day?
(A) 264 cm
(B) 88 cm
(C) 132 cm
(D) 176 cm
Solution:
(A) 264 cm
Explanation: Length of hour hand = Radius of the circle so formed = 21 cm.
In 1 Day, hour hand makes two round of the clock then hour hand makes an angle of 720°.
Distance covered by the tip of the hour hand
\(\begin{aligned}
& =\frac{\theta}{360^{\circ}} \times 2 \pi r \\
& =\frac{720^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7} \times 21 \\
& =264 \mathrm{~cm}
\end{aligned}\)
Question 15.
A card is selected at random from a well shuffled deck of 52 cards. The probability of its being a red face card is
(A) \(\frac{3}{26}\)
(B) \(\frac{3}{13}\)
(C) \(\frac{2}{13}\)
(D) \(\frac{1}{2}\)
Solution:
Option (A) is correct
Explanation: Total outcomes,
n(S) = 52
Number of red face cards = 6
i.e., Favourable outcomes, n(A) = 6
∴ P(a red face card) = \(\begin{aligned}
& \frac{n(A)}{n(S)} \\
& =\frac{6}{52}=\frac{3}{26}
\end{aligned}\)
Question 16.
For the following distribution :

The upper limit of the modal class is
(A) 10
(B) 15
(C) 20
(D) 25
Solution:
(C) 20
Explanation: Class interval of given highest frequency is 15–20.
Hence, the upper limit of the modal class is 20.
Question 17.
During conversion of a solid from one shape to another, the volume of new shape will
(A) increase
(B) decrease
(C) remains unaltered
(D) be doubled
Solution:
(C) remains unaltered
Explanation: During reshaping a solid, the volume of new solid will be equal to old one or remains unaltered.
Question 18.
Find the class marks of the classes 20-50 and 35 – 60.
(A) 35, 47.5
(B) 35,45
(C) 30475
(D) 30,45
Solution:
(A) 35, 47.5
Explanation: Class mark of 20 – 50 = \(\begin{aligned}
& \frac{20+50}{2} \\
& =\frac{70}{2}=35
\end{aligned}\)
and Class mark of 35 – 60 = \(\begin{aligned}
& \frac{35+60}{2} \\
& =\frac{95}{2}=47.5 .
\end{aligned}\)
Directions: In the following questions, A Statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
Question 19.
Assertion (A): √a is an irrational number, when a is a prime number.
Reason (R): Square root of any prime number is an irrational number.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A)is true but (R) is false.
(D) (A)is false but (R) is true.
Solution:
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
Explanation: √2, √3, √11 are irrational, also 2, 3 and 11 are prime.
But √4 =2 which is rational number but 4 is composite
Question 20.
Assertion (A): The point A is on the y-axis at a distance of 4 units below the origin. If the coordinates of point B are (3, 0). Then Length of AB is 5 units.
Reason (R) : Distance between the point A(x1, y1) and B(x2, y2) is \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).

Section -B(10 Marks)
Question 21.
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Shristi paid ₹ 27 for a book kept for seven days, while Rekha paid ₹ 21 for the book she kept for five days. Find the fixed charge and the additional charge paid by them.
Solution:
Let fixed charges for reading book = ₹ x
Let additional charges per day = ₹ y
then
x + 4y = 27 …(i)
x + 2y = 21 …(ii)
On solving both the equations
x = ₹ 15 and y = ₹ 3
Hence, Shristi paid additional charges = ₹ 12
Rekha paid additional charges = ₹ 6
![]()
Question 22.
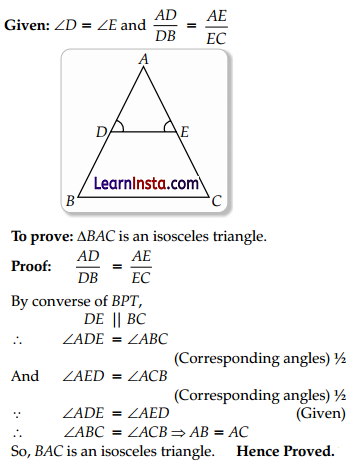
In the adjoining figure, ∠D= ∠E and \(\frac{A D}{D B}=\frac{A E}{E C}\)
Prove that ΔBAC is an isosceles triangle.
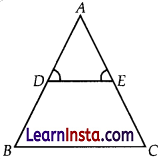
Solution:
OR
D and E are points on the sides AB and AC respectively of a ΔABC such that DE || BC.
Find the value of x, if AD = 7x – 4 cm, AE = 5x – 2.cm, DB = 3x + 4cm & EC = 3x cm.
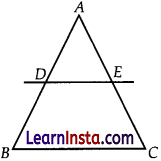
Solution:
In ∆ABC, DE || BC,
According to basic proportionality theorem,
\( \begin{aligned}
\frac{A D}{D B} & =\frac{A E}{E C} \\
\frac{(7 x-4)}{(3 x+4)} & =\frac{(5 x-2)}{3 x}
\end{aligned}\)
⇒ (7x – 4)(3x) =(5x – 2)(3x + 4)
⇒ 21x2 – 12x =15x2 + 20x – 6x – 8
⇒ 21x2 – 12x – 15x2 – 20x + 6x + 8 = 0
⇒ 6x2 – 26x+8 = 0
⇒ 3x2 – 13x+4 = 0
⇒ 3x2 – 12x – 1x + 4 =0
⇒ 3x(x – 4) –1(x – 4) =0
⇒ (3x – 1)(x – 4) =0
⇒ x = 4, 1/3
Question 23.
Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
Solution:
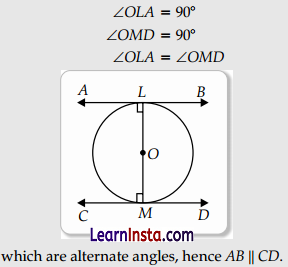
Question 24.
The tops of two towers of height x and y, standing on the ground, subtend the angles of 30° and 60° respectively at the centre of the line joining their feet, then find x: y.
Solution:

Question 25.
Shown below are two overlapping sectors of a circle. The radii of the sectors are 6 cm and 8 cm. The figure is divided into three regions-I, II, and III
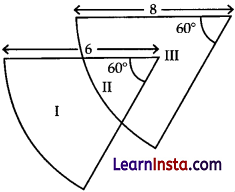
(Note: The figure is not to scale).
Find the difference in the areas of regions I and III. Show your work.
(Note: Take π = \(\frac{22}{7}\))
Solution:

OR
A sector of a circle has a central angle of 120 degrees and a radius of 10 cm. Calculate the area of the sector, the length of its arc and the perimeter of the sector’s arc.
Solution:

Therefore, the perimeter of the sector’s arc is \(\left(\frac{60+20 \pi}{3}\right)\) cm
Section -C(18 Marks)
Question 26.
Three sets of English, Hindi and Sociology books dealing with cleanliness have to be stacked in such a way that all the books are stored topic wise and the height of each stack is the same. The number of English books is 96, the number of Hindi books is 240 and the number of sociology books is 336.
(i) Assuming that the books are of the same thickness, determine the number of stacks of English, Hindi and Sociology books.
(ii) Which mathematical concept is used in the problem?
Solution:
(i) In order to arrange the books as required, we have to find the largest number that divides 96, 240 and 336 exactly, clearly, such a number is their HCF.
We have, by prime factorisation
96 = 25 × 3
240 = 24 × 3 × 5
and 336 = 24 × 3× 7
∴ HCF of 96, 240, and 336 is 24 × 3 = 48
So, there must be 48 books in each stack.
Number of stacks of English books
= \( \frac{96}{48}\)
= 2
Number of stacks of Hindi books
= \( \frac{240}{48}\)
= 5
Number of stacks of Sociology books
= \( \frac{336}{48}\)
= 7
(ii) HCF of numbers.
![]()
Question 27.
If the sum of zeroes of a quadratic polynomial ky2 + 2y – 3 is equal to twice their product, find the value of k.
Solution:

Question 28.
If the pth term of an A.P is \(\frac{1}{q}\) and qth term is \(\frac{1}{p}\) Prove that the sum of first pq term of the A.P. is \(\left[\frac{p q+1}{2}\right]\)
Solution:

OR
If the sum of first 14 terms of an A.P is 1050 and its first term is 10, find the 20th term.
Solution:
Given,
In A.P., S14 = 1050
a = 10
a20 = ?
∴ Sn = \(\frac{n}{2}\)[2a + (n – 1)d]
⇒ S14 = \(\frac{14}{2}\)[2 × 10 + (14 – 1)d]
⇒ 1050 = 7(20 + 13d)
⇒ 150 = 20 + 13d
⇒ 130 = 13d ⇒ d = 10
∴ an = a + (n – 1)d
∴ a20 = 10 + (20 – 1) × 10
= 10 + 19 × 10
= 200
Question 29.
(A) In figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.
Solution:
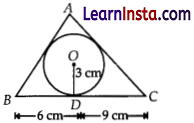
(B) Also find the perimeter of the triangle ABC.
Solution:
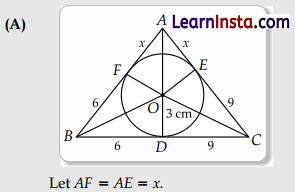
∴ AB = 6 + x, AC = 9 + x and BC = 15
ar ΔABC = \(\frac{1}{2}\)[15 + 6 + x + 9 + x].3 = 54
45 + 3x = 54
Or, x = 3
∴ AB = 9 cm, AC = 12 cm and BC = 15 cm.
(B) Perimeter of ∆ABC = AB + BC + CA = 9 + 12 + 15 = 36 cm
Question 30.
Prove that: = \(\frac{\sin \theta-\cos \theta}{\sin \theta+\cos \theta}+\frac{\sin \theta+\cos \theta}{\sin \theta-\cos \theta}=\frac{2}{2 \sin ^2 \theta-1}\)
Solution:

OR
Prove that: \(\frac{\cos A}{1+\tan A}-\frac{\sin A}{1+\cot A}\) = cos A – Sin A.
Solution:

Question 31.
Two different dice are thrown together. Find the probability that the number obtained.
(i) have a sum less than 7.
(ii) have a product less than 16.
(iii) is a doublet of odd numbers.
Solution:
Total number of all possible outcomes = 62 = 36
(i) The sum less than 7 = (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (5, 1)
No. of favourable outcomes = 15
P(have sum less than 7) = \(\frac{15}{36}=\frac{5}{12}\)
(ii) Product less than 16 = (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 2), (4, 3), (5, 1), (5, 2), (5, 3), (6, 1), (6, 2)
No. of favourable out outcomes = 25
∴ P(have a product less than 16) = \(\frac{25}{36}\)
(iii) Doublet of odd numbers = (1, 1), (3, 3), (5, 5)
No. of favourable outcomes = 3
∴ P(a doublet of odd number) = \(\frac{3}{36}=\frac{1}{12}\)
![]()
Section-D(20 Marks)
Question 32.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.
Solution:
Let the average speed of passenger train = x km/h. and the average speed of express train = (x + 11) km/h
As per given data, time taken by the express train to cover 132 km is 1 hour less than the passenger train to cover the same distance. Therefore,
\(\begin{aligned}
\frac{132}{x}-\frac{132}{x+11} & =1 \\
\frac{132(x+11-x)}{x(x+11)} & =1 \\
\frac{132 \times 11}{x(x+11)} & =1
\end{aligned}\)
⇒ 132 × 11 = x(x + 11)
⇒ x² + 11x – 1452 = 0
⇒ x² + 44x – 33x – 1452 = 0
⇒ x (x + 44) – 33(x + 44) = 0
⇒ (x + 44)(x – 33) = 0
⇒ x = – 44, 33
As the speed cannot be negative, the speed of the passenger train will be 33 km/h and the speed of the express train will be 33 + 11 = 44 km/h
OR
A motor boat whose speed is 18 km/h in still water takes 1 hour more to go 24 km upstream than to return down-stream to the same spot. Find the speed of the stream.
Solution:
Let the speed of the stream be x km/h.
So, the speed of the boat in upstream = (18 – x) km/h and the speed of the boat in downstream = (18 + x) km/h

Question 33.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and XY’ at B. Prove that ∠AOB = 90°.
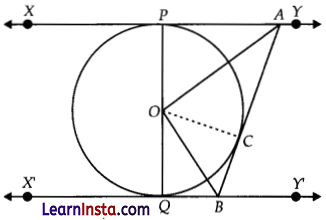
Solution:
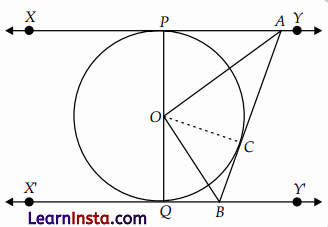
Given: A circle with centre O, XY || X’Y’
To prove: ∠AOB = 90°
Construction: Join OC
Proof: In ∆AOP & ∆AOC
OP = OC (Radius)
OA = OA (Common)
∠APO =∠ACO (each 90°)
By RHS Rule, ∆AOP ≅ ∆AOC
∠POA =∠COA (By CPCT) ..(i)
Similarly, ∆BOQ ≅ ∆BOC
Also, ∠BOC =∠BOQ (By CPCT) …(ii)
As, PQ is a diameter,
∠POA + ∠COA + ∠BOC + ∠BOQ = 180°
Or, 2∠COA+2∠BOA =180°
Or, 2∠AOB = 180°
Or, ∠AOB = 90°
Question 34.
Find the area of the shaded region in figure, \(\widehat{A P D}, \widehat{A Q B}, \overparen{B R C} \text { and } \widehat{C S D}\), are semi-circles of diameter 14cm, 3.5 cm, 7 cm and 3.5 cm respectively. (use π = \(\frac{22}{7}\)) :
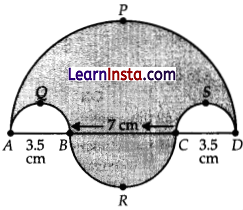
Solution:

OR
The internal and external diameters of a hollow hemispherical vessel are 16 cm and 12 cm respectively. If the cost of painting 1 cm’ of the surface area is ₹ 5.00, find the total cost of painting the vessel all over. (Use p = 3.14)
Solution:

Total Surface area = 2πR2 + 2πr2 + π(R2 – r2)
= p[82 × 2 + 62 × 2 + (82 – 62)]
= p[64 × 2 + 36 × 2 + (64 – 36)]
= p[128 + 72 + 28]
= 228 π cm2
= 228 × 3.14
= 715.92 cm2
Total cost of painting = ₹ 715.92 × 5 = ₹ 3579.60
![]()
Question 35.
The mean of the following distribution is 132 and the sum of the frequencies is 50. Find the missing frequency.
| Class | Frequency |
| 0-40 | 4 |
| 40-80 | 7 |
| 80-120 | x |
| 120-160 | 12 |
| 160-200 | y |
| 200-240 | 9 |
| Total | 50 |
Solution:
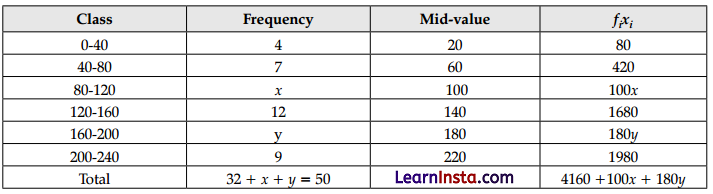
Sum of all frequencies = 32 + x + y = 50
Or, x + y = 18 …(i)
Mean = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)
132 = \(\frac{(4160+100 x+180 y)}{50}\)
6600 = 4160 + 100x + 180y
100x+180y = 6600 – 4160
100x + 180y = 2440
Or, 5x + 9y = 122 …(ii)
Multiply equation (i) with 5 and subtract from (ii), we get
4y = 32
Or, y = 8
Put in (i), we get
x =10
Section -E(12 Marks)
Question 36.
Amit is buying house and its layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq.m.
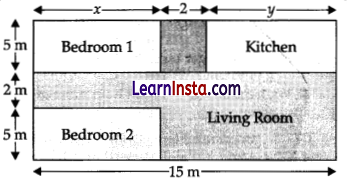
Based on the above situation answer the following questions.
(i) Frame the equations based on above layout.
(ii) Find the area of each bedroom and kitchen in the ground.
Solution:
(i) Area of two bedrooms = 2 × area of 1 bedroom = 10 x sq.m
Area of kitchen = 5 y sq.m
According to the figure, 10x + 5y = 95 (given)
Or, 2x + y = 19
Also, x + 2 + y = 15
(opposite sides of the rectangle)
Or, x + y = 13
(ii) 2x + y = 19 and x + y = 13
Subtracting both equations,
2x + y = 19
x + y = 13
– – –
x = 6m
Put in second equation, we get we get y = 7m
area of bedroom = 5 × 6 = 30 m²
Area of Kitchen = 5 × 7 = 35 m².
OR
Find the area of living room in layout.
(iii) Find the cost of laying tiles in the kitchen at the rate of ₹ 50 per square metre.
Solution:
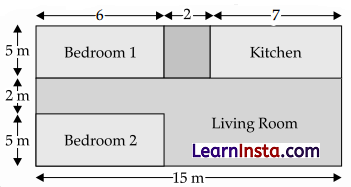
Area of kitchen = length x Breadth = 5 × 7 = 35 m²
Area of two bedroom = 2 × Area of 1 bedroom = 2 (5 × 6) = 60 m²
Area of Extra space between first Bedroom and kitchen = 5 × 2 = 10 m²
Area of layout = 15 × 12 = 180 m²
Area of living room in layout = 180 – 35 – 60 – 10 = 180 – 105 = 75 m²
(iii) Area of kitchen = 35 m².
Cost of laying tiles = Area of kitchen × Cost of laying tiles in 1 m² = 35 × 50 = ₹ 1750
Question 37.
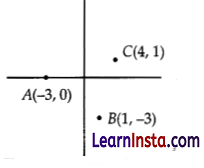
Based on above graph, answer the following questions :
(i) Find the length of side AB.
(ii) Find the midpoint of AC
(iii) Find the length of median from A to BC:
Solution:
(i) Coordinates of Vertices of triangle ABC are A(–3, 0), B(1, –3) and C(4, 1)

OR
Find the type of triangle formed by joining all three points.
Solution:

Also, it verifies Pythagoras theorem, AC² = AB² + BC² therefore, the triangle in the graph is isosceles right angled triangle.
![]()
Question 38
A fast jet-powered military aircraft designed for attacking other aircraft. Domination of the airspace above a battle filed permits bombers and attack aircraft to engage in tactical and strategic bombing of enemy targets. The united States Air Force is composed of 5217 active aircraft making it the largest, the most technologically advanced, and the most powerful air fleet in the world. The angle of elevation of a jet fighter from point A on ground is 60°. After flying 10 seconds, the angle changes to 30°. If the jet is flying at a speed of 648 km/h.

Based on the above situation, answer the following questions :
(i) Which mathematical concept used in this case?
(ii) Find the distance in meter travelled by Jet in 10 seconds.
Solution:
(i) Applications of Trigonometry or Height and Distance.
(ii) ∴ 1 hour = 60 × 60 = 3600 seconds. and 1 km = 1000 m
∴ Distance travelled by a jet in 3600 sec = 648000 m
Distance travelled by a jet in 10 sec \(=\frac{648000}{3600} \times 10\) = 1800 m
OR
According to case, the figure is:
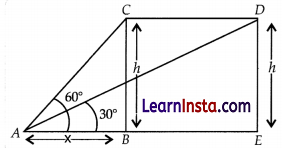
Then find the value of x.
(iii) From the figure of question 2, find the constant height at which the Jet is flying.
Solution:
