By going through these CBSE Class 11 Maths Notes Chapter 8 Binomial Theorem Class 11 Notes, students can recall all the concepts quickly.
Binomial Theorem Notes Class 11 Maths Chapter 8
Binomial theorem for any positive integer
1. (a + b)n = nC0an + nC1an-1 + nC2an-2 + ………………..nCran-rbr + ………..+ nCnbn
2. Tr+1 = general term = nCran-rbr … (1)
(a + b)n = \(\sum_{r=0}^{n}\)nCran-rbr
3. Some observations : (i) Number of terms in binomial expansion = Index of the binomial + 1 = n + 1.
(ii) In the successive terms of the expansion, the index of the first term is n and it goes on decreasing by unity. Thus, the indices of first term and n, n – 1, n – 2, …, 1, 0 while the index of second term starts from 0 and goes on increasing by 1. Therefore, the indices of second term are 0, 1, 2, … , n.
(iii) In any term of the expansion, the sum of indices of first term and second term is constant and it is equal to n.
(iv) Coefficients of these terms in the expansion are nC0, nC1, nCr. ……, nC2….., nCn
Note : These coefficients may also be denoted as
C (n, 0), C(n, 1), C (n, 2),…, C (n, r), …, C (n,n).
To find their values, we apply the formula
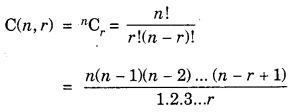
Whenever r > \(\frac{n}{2}\) , apply the formula
nCr = nCn-r
These coefficients may also be obtained with the help of Pascal’s triangles.
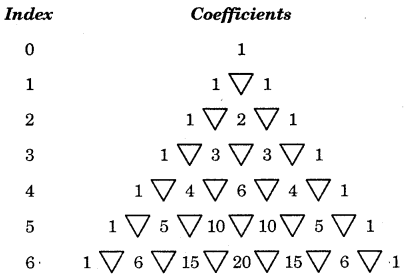
Now look at this pattern :
(a) First row; index 0; coefficient = 1.
(b) Second row; index 1; coefficients are 1, 1. A triangle is inserted between 1 and 1 as shown above.
(c) Third row; index 2; coefficients are 1, 2, 1.
Method : Two triangles, are drawn below each number of 1 of the second row. Adding 1 and 1 of second row we get 2 which is put below the third vertex of triangle. Write 1 each at the beginning arid end.
(d) Fourth row, index 3; coefficients are 1, 3, 3, 1. Method : Insert three triangles below 1, 2 and 1. 1 + 2 = 3 is written below the third vertex of first triangle, 2 + 1 = 3 is written below the second triangle.
Further, we proceed in the same manner.
(v) Coefficients nC0, nC1, nC2…, nCr, nCn in Binomial Theorem are known as Binomial Coefficients.
(vi) Replacing b by – b, in (1), we obtain
(a-b)n = nC0an – nC1an-1b + nC2an-2b2 + ……….(-1)ⁿⁿCran-rbr + ……….nCn(-b)n
(vii) Putting a = 1, b = x in (1), we obtain
(1+x)n = nC0 + nC1x + nC2x2 + ……nCrxr + …….. + nCnxn
(viii) Putting a = 1, b = – x in (1), we obtain
(1-x)n = nC0 – nC1x + nC2x2 – ….+nCr(-x)r + …… + nCn(-x)n
(ix) Putting a = 1, b = 1 in (1), we obtain
(1+1)n = 2n = nC0 + nC1 + nC2 + ………..+nCn
(x) Putting a = 1, b = – 1, we obtain
0 = nC0 – nC1 + nC2 – nC3 + …..
or nC0 + nC2 + nC4 + ….. = nC1 + nC3 + …………+ nCr + ………
4. Middle Term : The expansion (a + b)n has n + 1 terms.
(i) If n + 1 is odd, the middle term is th = \(\frac{(n+1)+1}{2}\) th \(\frac{(n+2)}{2}\)th term.
(ii) If n + 1 is even, then
1st middle term = \(\frac{n+1}{2}\)th term
2nd middle term = \(\left(\frac{n+1}{2}+1\right)\)th term