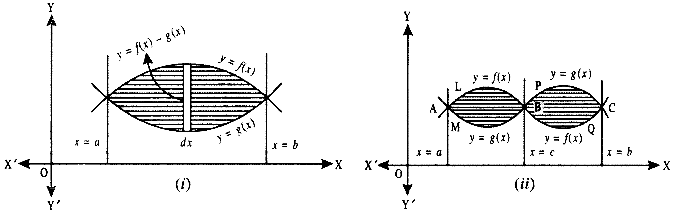By going through these CBSE Class 12 Maths Notes Chapter 8 Application of Integrals, students can recall all the concepts quickly.
Application of Integrals Notes Class 12 Maths Chapter 8
Area under Simple curves:
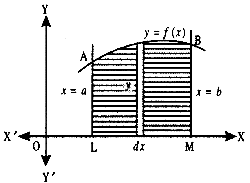
1. Let us find the area bounded by the curve y = f(x), x-axis, and the ordinates x = a and x – b. Consider the area under the curve as composed of a large number of thin vertical stripes.
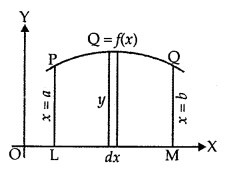
Let there be an arbitrary strip of height y and width dx.
Area of elementary strip dA = y dx, where y = f(x).
Total area A of the region between x-axis, ordinates x – a, x = b and the curve y = f(x)
= sum of areas of elementary thin strips across the region PQML.
A = ∫ab dA = ∫ab ydx = ∫ab f(x) dx.
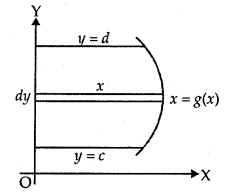
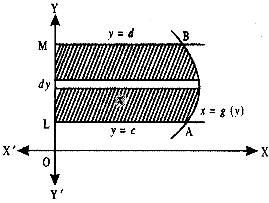
2. The area A of the region bounded by the curve x = g(y), y-axis, and the lines
y = c and y = d is given by
A = ∫cd x dy
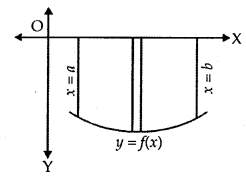
3. If the curve under consideration lies below x-axis, then f(x) < 0 from x = a to x = b. So, the area bounded by the curve y = f(x) and the ordinates x = a, x = b and x-axis is negative. But the numerical value of the area is to be taken into consideration.
Then, area = |∫ab f(x)dx|.
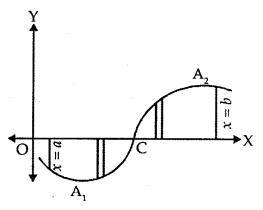
4. It may also happen that some portion of the curve is above the x-axis and some portion is below the x-axis as shown in the figure. Let A1 be the area below the x-axis and A2 be the area above the x-axis. Therefore, area A bounded by the curve y = f(x), x-axis and the ordinates x = a and x = b is given by
A = |A1| + A2.
Area between two curves:
1. Let the two curves by y = f(x) and y = g(x), as shown in the figure. Suppose these curve intersect at x = a and x = b.
Consider the elementary strip of height y where y = f(x) – g(x), with width dx.
∴ dA = y dx.
⇒ A = ∫ab (f(x) – g(x))dx
= ∫ab f(x) dx – ∫ab g(x) dx.
= Area bounded by the curve y = f(x) – Area bounded by the curve y = g(x), where f(x) > g(x).
2. If the two curves y = f(x) and y = g(x) intersect at x-a,x – c and x = b such that a < c < b, then:
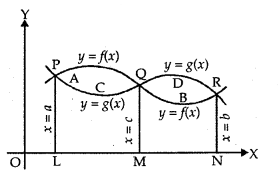
If f(x) > g(x) in [a, c] and f(x) < g(x) in [c, b], then the area of the regions bounded curve
= Area of the region PAQCP + Area of the region QDRBQ
= ∫ac f(x) – g(x)) dx + ∫cb (g(x) – f(x)) dx.
1. Area Under Simple Curves
(i) Area of the region bounded by the curve y = f (x), x-axis and the linesx = a and x = b(b > a) is given by the formula:
Area = \(\int_{a}^{b}\) ydy = \(\int_{a}^{b}\) f(x) dy.
2. Area of the region bounded by the curve x = g(x), y-axis and the lines y = c,y = d is given by the formula:
Area = \(\int_{c}^{d}\) xdy = \(\int_{c}^{d}\) g(y) dy.
2. Area Between two Curves
(i) Area of the region enclosed between two curves y = f (x), y = g (x) and the lines x = a, x = b is
\(\int_{a}^{b}\) [f(x) -g(x)] dx, where f(x) ≥ g (x) in [a, b],
(ii) Iff (x) ≥ g (x) in [a, c] and f(x) ≤ g (x) in [c, b], a < c < b, then we write the area as:
Area = \(\int_{a}^{c}\) [f(x) – g(x)] dx + \(\int_{c}^{b}\) [g(x) – f(x)] dx.