Wave Particle Duality of Matter

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Wave Particle Duality of Matter

Albert Einstein proposed that light has dual nature. i.e. light photons behave both like a particle and as a wave. Louis de Broglie extended this concept and proposed that all forms of matter showed dual character. To quantify this relation, he derived an equation for the wavelength of a matter wave. He combined the following two equations of energy of which one represents wave character (hυ) and the other represents the particle nature (mc²).

(i) Planck’s quantum hypothesis:
E = hυ ……………. (2.6)

(ii) Einstein’s mass-energy relationship
E = mc² …………….. (2.7)

From (2.6) and (2.7)

hν = mc²
hc/λ = mc²
λ = h/mc …………….. (2.8)

The equation 2.8 represents the wavelength of photons whose momentum is given by mc (Photons have zero rest mass)

For a particle of matter with mass m and moving with a velocity v, the equation 2.8 can be written as
λ = h/mv ………………. (2.9)

This is valid only when the particle travels at speeds much less than the speed of Light.

This equation implies that a moving particle can be considered as a wave and a wave can exhibit the properties (i.e momentum) of a particle. For a particle with high linear momentum (mv) the wavelength will be so small and cannot be observed. For a microscopic particle such as an electron, the mass is of the order of 10^-31 kg, hence the wavelength is much larger than the size of atom and it becomes significant.

Let us understand this by calculating de Broglie wavelength in the following two cases:

• A 6.626 kg iron ball moving at 10 ms^-1
• An electron moving at 72.73 ms^-1

λ_ironball= h/mv

λ_electron= h/mv

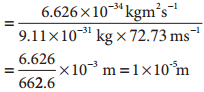
For the electron, the de Broglie wavelength is significant and measurable while for the iron ball it is too small to measure, hence it becomes insignificant.

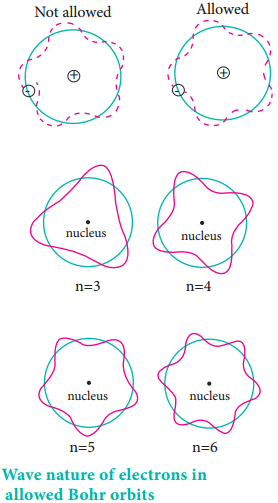
According to the de Broglie concept, the electron that revolves around the nucleus exhibits both particle and wave character. In order for the electron wave to exist in phase, the circumference of the orbit should be an integral multiple of the wavelength of the electron wave. Otherwise, the electron wave is out of phase.

Circumference of the orbit = nλ

2πr = nλ ……………… (2.10)
2πr = nh/mv

Rearranging,
mvr = nh/2π …………… (2.11)

Angular momentum = nh/2π

The above equation was already predicted by Bohr. Hence, De Broglie and Bohr’s concepts are in agreement with each other.

Davison and Germer Experiment:

The wave nature of electron was experimentally confirmed by Davisson and Germer. They allowed the accelerated beam of electrons to fall on a nickel crystal and recorded the diffraction pattern. The resultant diffraction pattern is similar to the x-ray diffraction pattern. The finding of wave nature of electron leads to the development of various experimental techniques such as electron microscope, low energy electron diffraction etc.