Here we are providing Surface Areas and Volumes Class 9 Extra Questions Maths Chapter 13 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers.
Extra Questions for Class 9 Maths Surface Areas and Volumes with Answers Solutions
Extra Questions for Class 9 Maths Chapter 13 Surface Areas and Volumes with Solutions Answers
Surface Areas and Volumes Class 9 Extra Questions Very Short Answer Type
Question 1.
How much ice-cream can be put into a cone with base radius 3.5 cm and height 12 cm?
Solution:
Here, radius (r) = 3.5 cm and height (h) = 12 cm
∴ Amount of ice-cream = \(\frac{1}{3}\) πr2
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3.5 × 3.5 × 12
= 154 cm3
Question 2.
Calculate the edge of the cube if its volume is 1331 cm3.
Solution:
Volume of cube = 1331 cm3
(Side)3 = 1331
Side = (11 × 11 × 11)\(\frac{1}{3}\) = 11 cm
Question 3.
The curved surface area of a cone is 12320 sq. cm, if the radius of its base is 56 cm, find its
height.
Solution:
Here, radius of base of a cone (r) = 56 cm
And, curved surface area = 12320 cm2
πrl = 12320
l = \(\frac{12320}{\pi r}\)
= \(\frac{12320 \times 7}{22 \times 56}\) = 70 cm
Again, we have
r2 + h2 = l2
h2 = l2 – r2 = 702 – 562
= 4900 – 3136 = 1764
h = √1764 = 42 cm
Hence, the height of the cone is 42 cm.
Question 4.
Two cubes of edge 6 cm are joined to form a cuboid. Find the total surface area of the cuboid.
Solution:
When two cubes are joined end to end, then
Length of the cuboid = 6 + 6 = 12 cm
Breadth of the cuboid = 6 cm
Height of the cuboid = 6 cm
Total surface area of the cuboid = 2 (lb + bh + hl)
= 2(12 × 6 + 6 × 6 + 6 × 12)
= 2(72 + 36 + 72) = 2(180)
= 360 cm2
Question 5.
A metallic sphere is of radius 4.9 cm. If the density of the metal is 7.8 g/cm2, find the mass of the sphere (π = \(\frac{22}{7}\)).
Solution:
Here, radius of metallic sphere (r) = 4.9 cm
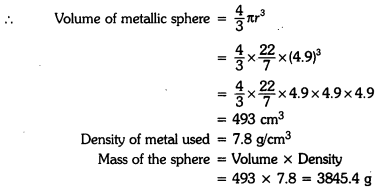
Question 6.
The volume of a solid hemisphere is 1152 π cm3. Find its curved surface area.
Solution:
Here, volume of hemisphere = 1152 π cm3
∴ \(\frac{2}{3}\)πr3 = 1152
⇒ r3 = (12)3 π
⇒ r\(\frac{1152 \times 3}{2}\) = 1728
⇒ r3 = (12)3
Now, curved surface area = 2πr2
= 2 × π × (12)2 = 288π cm2
Question 7.
Find the diameter of a cylinder whose height is 5 cm and numerical value of volume is equal to
numerical value of curved surface area.
Solution:
Here, height of cylinder (h) = 5 cm
According to the statement of the question, we have
πr2h = 2πrh
r = 2 cm
Thus, diameter of the base of the cylinder is 2 × 2 i.e., 4 cm.
Question 8.
In a cylinder, if radius is halved and height is doubled, then find the volume with respect to original volume.
Solution:
Here, r = \(\frac{r}{2}\), h = 2h
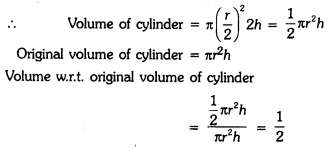
Surface Areas and Volumes Class 9 Extra Questions Short Answer Type 1
Question 1.
A spherical ball is divided into two equal halves. If the curved surface area of each half is 56.57 cm, find the volume of the spherical ball. [use π = 3.14]
Solution:
Since curved surface of half of the spherical ball = 56.57 cm2
2πr2 = 56.57

= 113.04 cm3
Question 2.
Find the capacity in litres of a conical vessel having height 8 cm and slant height 10 cm.
Solution:
Height of conical vessel (h) = 8 cm
Slant height of conical vessel (l) = 10 cm
∴ r2 + h2 = l2
⇒ r2 + 82 = 102
⇒ r2 = 100 – 64 = 36
⇒ r = 6 cm
Now, volume of conical vessel = \(\frac{1}{3}\)πr2h = \(\frac{1}{3}\) × \(\frac{22}{7}\) × 6 × 8 = 301.71 cm3 = 0.30171 litre
Question 3.
Calculate the surface area of a hemispherical dome of a temple with radius 14 m to be whitewashed from outside.
Solution:
Here, radius of hemispherical dome (r) = 14 m
Surface area of dome = 2πr2
= 2 × \(\frac{22}{7}\) × 14 × 14 = 1232 m2
Hence, total surface area to be whitewashed from outside is 1232 m2.
Question 4.
A rectangular piece of paper is 22 cm long and 10 cm wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.
Solution:
Since rectangular piece of paper is rolled along its length.
∴ 2πr = 22
r = \(\frac{22 \times 7}{2 \times 22}\) = 3.5 cm
Height of cylinder (h) = 10 cm
∴ Volume of cylinder = πr2h
= \(\frac{22}{7}\) × 3.5 × 3.5 × 10 = 385 cm3
Question 5.
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find it volume. If 1m3 wheat cost is ₹10, then find total cost.
Solution:
Diameter of cone = 10.5 m
Radius of cone (r) = 5.25 m
Height of cone (h) = 3 m
Volume of cone = \(\frac{1}{3}\)πr2h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 5.25 × 5.25 × 3
= 86.625 m3
Cost of 1m3 of wheat = ₹10
Cost of 86.625 m3 of wheat = ₹10 × 86.625
= ₹866.25
Question 6.
A cylindrical vessel can hold 154 g of water. If the radius of its base is 3.5 cm, and1cm3 of water weighs 1 g, find the depth of water.
Solution:
Since 1 cm3 of water weighs 1 g.
∴ Volume of cylindrical vessel = 154 cm3
πr2h = 154
\(\frac{22}{7}\) × 3.5 × 3.5 × h = 154
h = \(\frac{154 \times 7}{22 \times 3.5 \times 3.5}\)
h = 4
cm Hence, the depth of water is 4 cm.
Surface Areas and Volumes Class 9 Extra Questions Short Answer Type 2
Question 1.
A wall of length 10 m is to be built across an open ground. The height of the wall is 5 m and thickness of the wall is 42 cm. If this wall is to be built with brick of dimensions 42 cm × 12 cm × 10 cm, then how many bricks would be required?
Solution:
Here, length of the wall (L) = 10 m = 1000 cm
Breadth of the wall (B) = 42 cm
Height of the wall (H) = 5 m = 500 cm
∴ Volume of the wall = L × B × H
= 1000 × 42 × 500 cm3
Volume of each brick = 42 × 12 × 10 cm3
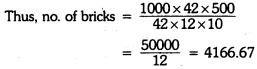
= 4167
Hence, the required number of bricks is 4167.
Question 2.
The volume of cylindrical pipe is 748 cm. Its length is 0.14 m and its internal radius is 0.09 m. Find thickness of pipe.
Solution:
Internal radius (r) of cylindrical pipe = 0.09 m = 9 cm
Length (height) of cylindrical pipe (h) = 0.14 m = 14 cm
Let external radius of the cylindrical pipe be R cm.
Volume of cylindrical pipe = 748 cm3
⇒ π(R2 – r2)h = 748
⇒ \(\frac{22}{7}\) (R2 – 92)14 = 748
⇒ R2 – 81 = \(\frac{748 \times 7}{22 \times 14}\) = 17
⇒ R2 = 81 + 17 = 98
⇒ R = √98 = 7√2 cm = 9.9 cm
Thus, thickness of the pipe = 9.9 -9 = 0.9 cm
Question 3.
The curved surface area of a cylinder is 154 cm. The total surface area of the cylinder is three times its curved surface area. Find the volume of the cylinder.
Solution:
Since curved surface area of cylinder = 154 cm2 (given]
Total surface area of cylinder = 3 × curved surface area
2πrh + 2πr2 = 3 × 154 3 154 + 2πr2 = 462
2πr2 = 462 – 154 = 308
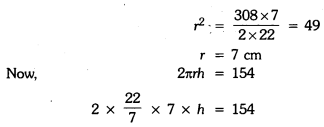

= 539 cm3
Question 4.
A right-angled ∆ABC with sides 3 cm, 4 cm and 5 cm is revolved about the fixed side of 4 cm. Find the volume of the solid generated. Also, find the total surface area of the solid.
Solution:
When rt. ∠ed ∆ABC is revolved about AB = 4 cm, it forms a right circular cone of radius 3 cm and height 4 cm. Slant height of the cone is 5 cm.
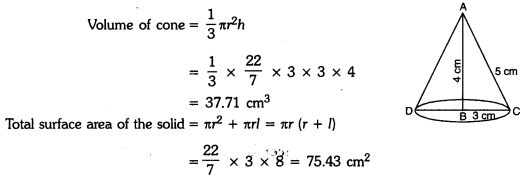
Question 5.
A semicircular sheet of metal of radius 14 cm is bent to form an open conical cup. Find the capacity of the cup.
Solution:
Radius of semicircular sheet (r) = 14 cm
∴ Slant height (1) = 14 cm
Circumference of base = Circumference of semicircular sheet
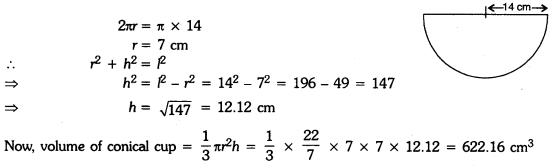
Surface Areas and Volumes Class 9 Extra Questions Long Answer Type
Question 1.
It costs ₹3300 to paint the inner curved surface of a 10 m deep well. If the rate cost of
painting is of ₹30 per m2, find :
(a) inner curved surface area
(b) diameter of the well
(c) capacity of the well.
Solution:
Depth of well (h) = 10 m
Cost of painting inner curved surface is ₹30 per m2 and total cost is ₹3300

Hence, inner curved surface area is 110 m2, diameter of the well is 2 × 1.75 i.e., 3.5 m and capacity of the well is 96.25 m3.
Question 2.
Using clay, Anant made a right circular cone of height 48 cm and base radius 12 cm. Versha reshapes it in the form of a sphere. Find the radius and curved surface area of the sphere so formed.
Solution:
Height of cone (h) = 48 cm
Radius of the base of cone = 12 cm
Let R be the radius of sphere so formed
∴ Volume of sphere = Volume of cone
\(\frac{4}{3}\)πR3 = \(\frac{1}{3}\)πr2h
4R3 = 12 × 12 × 48
R3 = 12 × 12 × 12
R = 12 cm
Now, curved surface area of sphere = 4πR2
= 4 × \(\frac{22}{7}\) × 12 × 12
= 1810.29 cm
Question 3.
A dome of a building is in the form of a hemisphere. From inside, it was whitewashed at the cost of ₹498.96. If the rate of whitewashing is ₹4 per square metre, find the :
(i) Inside surface area of the dome
(ii) Volume of the air inside the dome.
Solution:
Here, dome of building is a hemisphere.
Total cost of whitewashing inside the dome = ₹498.96
Rate of whitewashing = ₹4 per m2

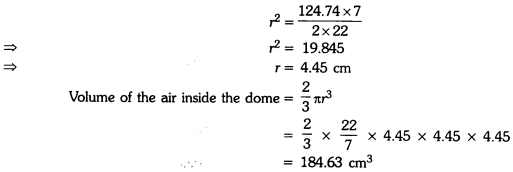
Question 4.
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 5 cm. Find the volume of the solid so obtained. If it is now revolved about the side 12 cm, then what would be the ratio of the volumes of the two solids obtained in two cases ?
Solution:
Here, right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 5 cm.
∴ Radius of the base of cone = 12 cm
Height of the cone = 5 cm
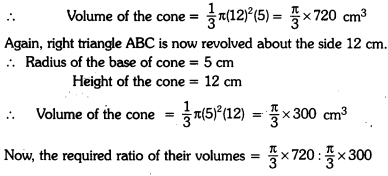
= 12 : 5
Question 5.
A right triangle of hypotenuse 13 cm and one of its sides 12 cm is made to revolve taking side 12 cm as its axis. Find the volume and curved surface area of the solid so formed.
Solution:
Here, hypotenuse and one side of a right triangle are 13 cm and 12 cm respectively.
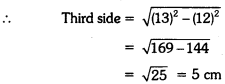
Now, given triangle is revolved, taking 12 cm as its axis
∴ Radius of the cone (r) = 5 cm
Height of the cone (h) = 12 cm
Slant height of the cone (1) = 13 cm
∴ Curved surface area = πrl = π(5)(13) = 65π cm2
Volume of the cone = \(\frac{1}{2}\)πr2h = \(\frac{1}{2}\)π × 5 × 5 × 12 = 100π cm3
Hence, the volume and curved surface area of the solid so formed are 100 π cm3 and 65 π cm2 respectively.
Surface Areas and Volumes Class 9 Extra Questions HOTS
Question 1.
Each edge of a cube is increased by 50%. Find the percentage increase in the surface area of the cube.
Solution:
Let each edge of the cube be a cm.

Question 2.
A rectangular tank is 225 m × 162 m at base. With what speed should water flow into it through an aperture 60 cm × 45 cm so that the level of water is raised by 20 cm in 2.5 hours?
Solution:
Volume of water to be flown in 2.5 hour
= 225 m × 162 m × 20 cm
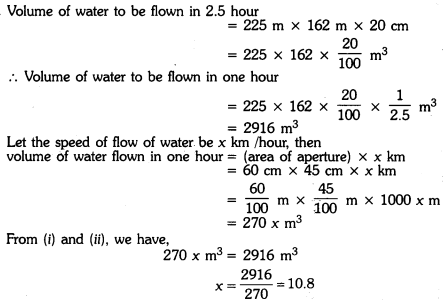
Hence, the speed of flow of water = 10.8 km/hour
Surface Areas and Volumes Class 9 Extra Questions Value Based (VBQs)
Question 1.
To maintain beauty of a monument, the students of the school cleaned and painted the dome of the monument. The monument is in the form of a hemisphere. From inside, it was white washed by the students whose area is 249.48 m2.
(a) Find the volume of the air inside the dome. If white washing costs ₹2 per m2, how much does it costs ?
(b) Which value is depicted by the students? (π = \(\frac{22}{7}\))
Solution:
(a) Here, dome of the monument is hemispherical in shape, which was whitewashed by the students.
Now, total area to be white washed = 249.48 m2
Cost of white washing = ₹2 per m2
∴ Total cost of white washing = ₹2 × 249.48
= ₹498.96
Also, 2πr2 = 249.48
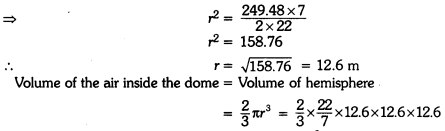
= 4191.264 m3
(b) Value: Cleanliness, beautification as well as preserving the heritage along with social values.
Question 2.
Salim provides water to a village, having a population of 4000 which requires 150 litres of water per head per day. He has storage tank measuring 20 m × 15 m × 6 m. For how many days will the water of his tank last? He increased the rate for providing water as the dependence of villagers increased on him. Which value is depicted by Salim?
Solution:
(i) Here, the population of the village = 4000
Requirement of water per head per day = 150 litres
∴ Total requirement of water per day = 4000 × 150 litres
= 600000 litres
Volume of water tank = 20 × 15 × 6
= 1800 m3
= 1800 × 1000 litres
Now, number of days for which water of the tank will last = \(\frac{1800 \times 1000}{600000}\) = 3 days
Hence, water tank can serve for 3 days.
(ii) Helping the needy.