Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22C
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22C
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22C
Question 1.
Find AD.
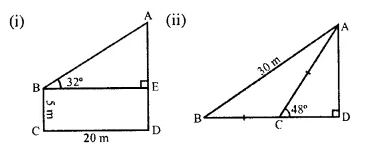
Solution:

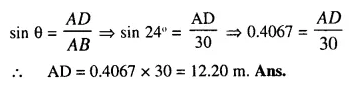
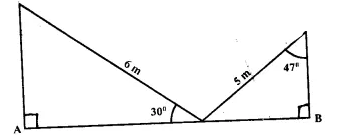
Question 2.
In the following diagram.
AB is a floor-board. PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
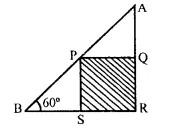
Solution:
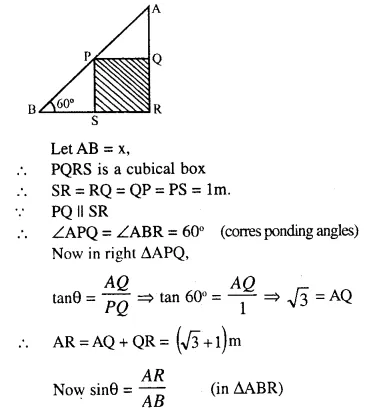
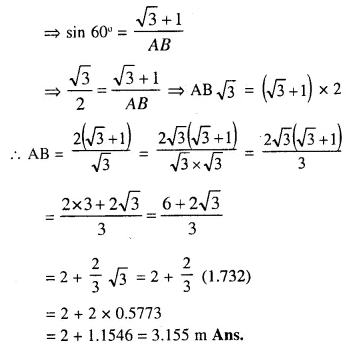
Question 3.
Calculate BC.
Solution:

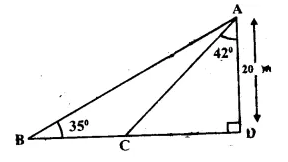
Question 4.
Calculate AB .
Solution:

Question 5.
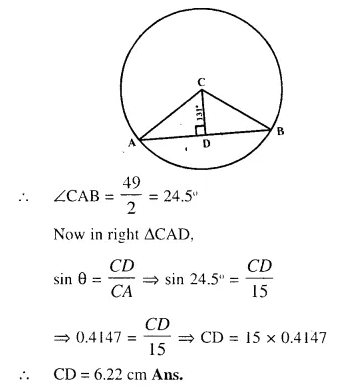
The radius of a circle is given as 15cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, Calculate :
(i) the length of AB;
(ii) the distance of AB from the centre C.
Solution:
Chord AD substends an angle of 131° at the centre. Join CA, CB and draw CD ⊥ AB which bisects AB at D.
(In ∆CAB)
∵ CA = CB (radii of the same circle)
∴ ∠CAB = ∠CBA
But ∠CAB + ∠CBA = 180°- 131° = 49°

Question 6.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is \(\frac { 5 }{ 12 }\). On walking 192 metres towards the tower; the tangent of the angle is found to be \(\frac { 3 }{ 4 }\). Find the height of the tower.
Solution:
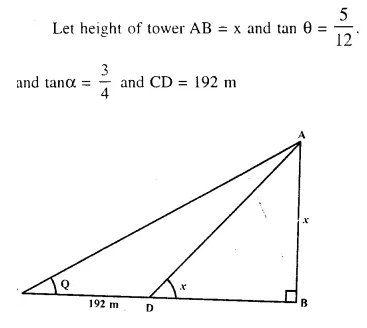
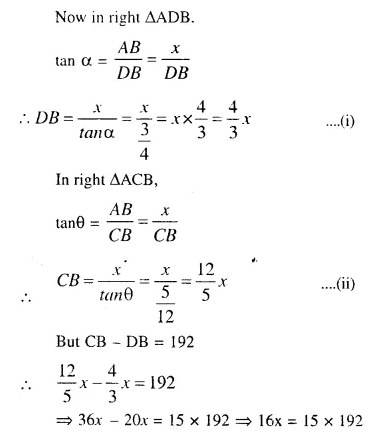
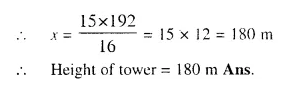
Question 7.
A vertical tower stands on horizontal plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is a and that of the top of flagstaff is β. Prove that the height of the tower is :
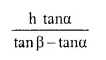
Solution:
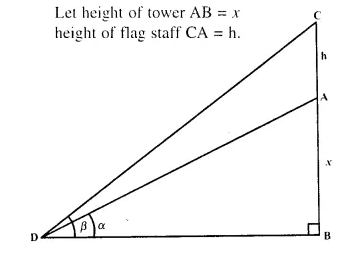
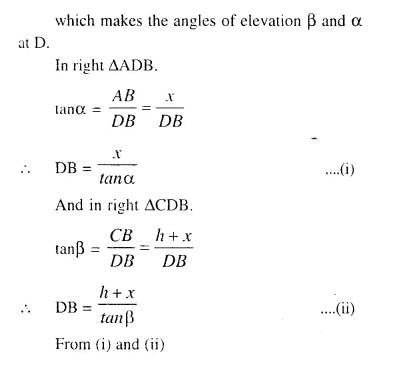
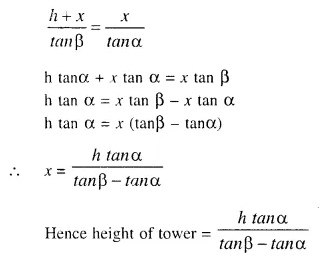
Question 8.
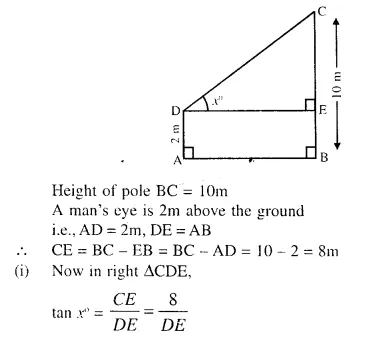
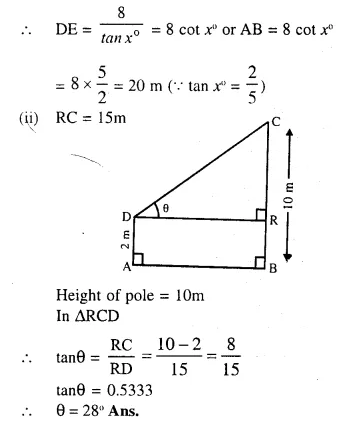
With reference to the given figure, a man stands on the ground at point A, which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m.
The man’s eye is 2 m above the ground. He observes the angle of elevation of C. The top of the pole, as x°, where tan x° = \(\frac { 2 }{ 5 }\) . calculate:
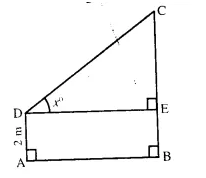
(i) the distance AB in m;
(ii) the angle of elevation of the top of the pole
when he is standing 15 m from the pole. Give your answer to the nearest degree. [1999]
Solution:
Question 9.
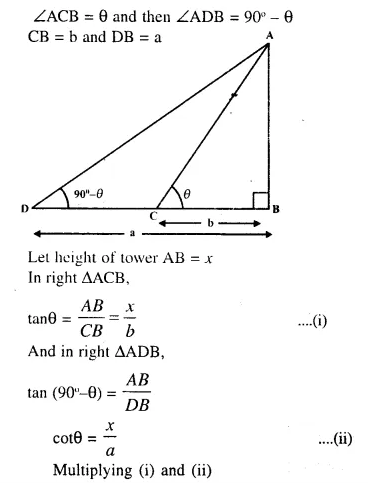
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same striaght line with it are complementary.Prove that height of the tower is \( \sqrt{ab} \) metre.
Solution:
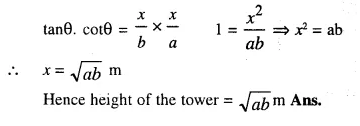
Question 10.
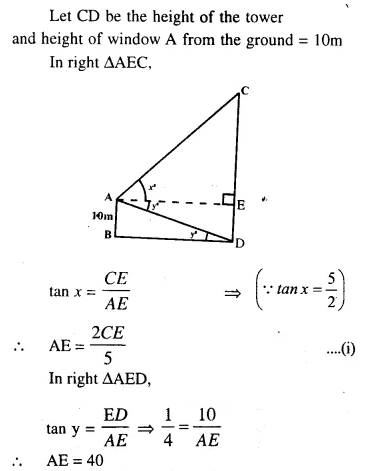
From a window A. 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan x = \(\frac { 5 }{ 2 }\) and the angle of depression of the foot D of the tower is y°, where tany° = \(\frac { 1 }{ 4 }\).(See the figure given below). Calculate the height CD of the tower in metres. [2000]
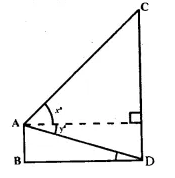
Solution:
Let CD be the height of the tower and height of window A from the ground = 10m
In right ∆AEC,
Question 11.
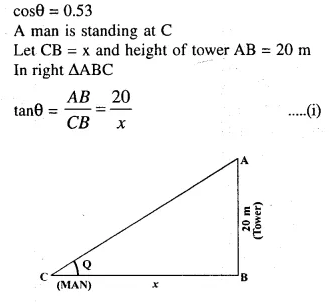
A vertical tower is 20 m high, A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower ? [2001]
Solution:

Question 12.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°. Calculate :
(i) the width of the river and
(ii) the height of the tree.
Solution:
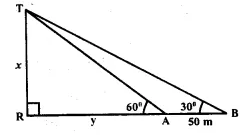
Let TR be the tree of height x m and y be the width AR of the river,
then ∠B = 30° and A = ∠60° , AB = 50 m.
Now in right ∆ATR,
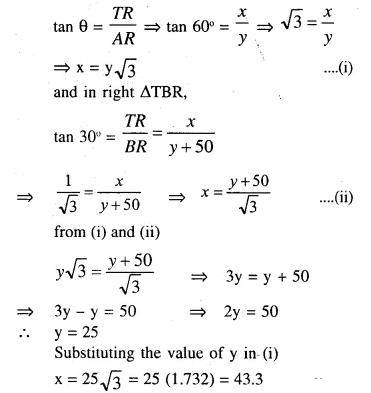
Question 13.
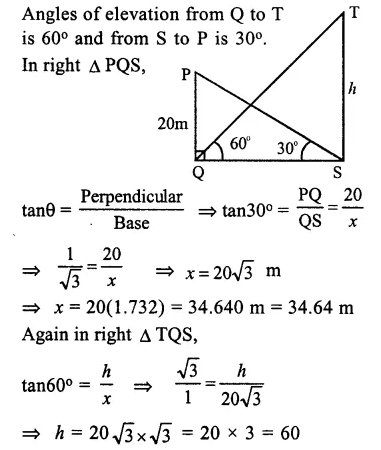
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is 60° and the angle of elevation of the top of the pole as seen from the foot of the tower is 30°. Find
(i) the height of the tower.
(ii) the horizontal distance between the pole and the tower.
Solution:
Let PQ is the pole and TS is the tower. PQ = 20 m.
Let TS = h and QS = x Angles of elevation from Q to T A T is 60° and from S to P is 30°.
In the ∆PQS
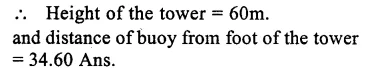
Question 14.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°.
Find : (i) the height of the tower, if the height of the pole is 20m;
(ii) the height of the pole, if the height of the tower is 75 m.
Solution:
Let PQ is the pole and TW is the tower
Angle of elevation from T to P is 60° and angle of depression from P to W is 30°
∴ ∠PWQ = 30° = ∠RPW ( ∠ Altanate angles)
(i) In first case when height of pole OQ = 20m, Then in right ∆ PQW

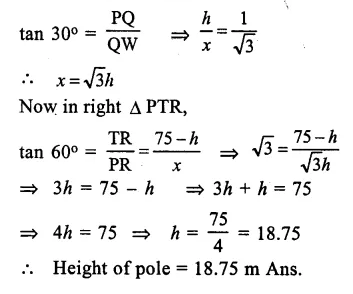
Question 15.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
Solution:
Let AQ is the sea-level
P is a point 36 m above sea-level
∴ PQ = 36
Let B be the bird and R is its reflection in the water and angle of elevation of the bird B at P is 30° and angle of depression of the reflection of the bird at R is 60°

![]()
Question 16.

Solution:

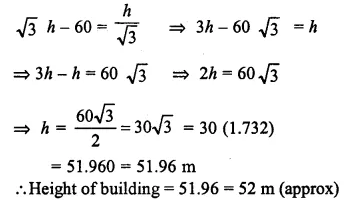
Question 17.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of the light house in horizontal line with its base , are 30° and 40° respectively . Find the distance between the two ships.Give your answer correct to the nearest meter. [2012]
Solution:
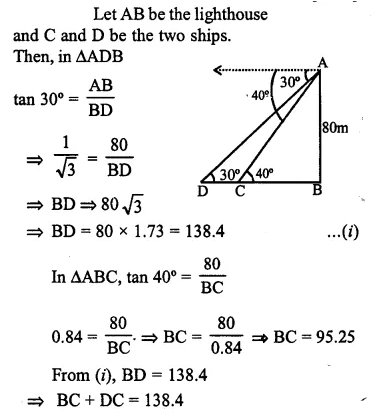

Question 18.
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find :
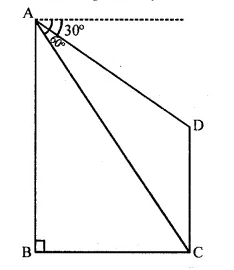
(i) the horizontal distance between AB and CD.
(it) the height of the lamp post.
Solution:
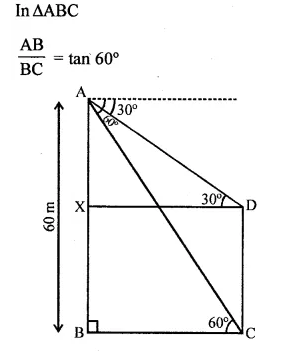

![]()
Question 19.
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number. (2014)
Solution:
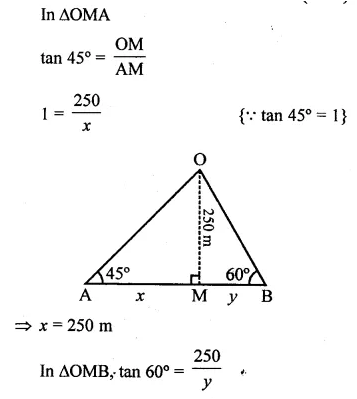
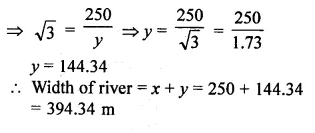
Question 20.
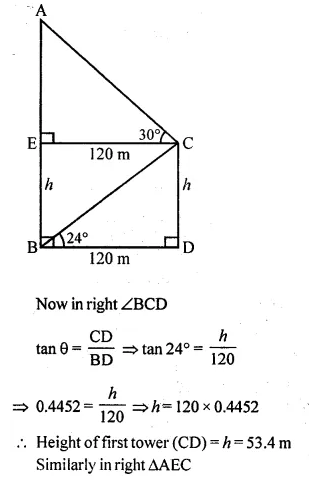
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second tower is 30° and 24° respectively. Find the height of the two towers. Give your answer correct to 3 significant figures. (2015)
Solution:
AB and CD are two towers which are 120 m apart
i.e. BD= 120m
Angles of elevation of the top and angle of depression of bottom of the first tower observed from the top of second tower is 30° and 24°

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.