RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.1
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.2
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.3
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles Ex 13.4
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS
- RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles MCQS
Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
Solution:
Diameter of a circle and side of an equilateral triangle are same
Let the diameter of the circle = a
Then radius (r) = \(\frac { a }{ 2 }\)
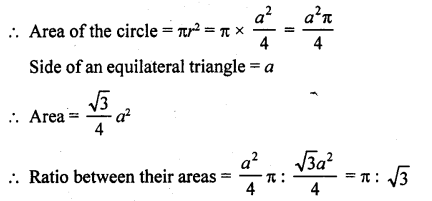
Question 2.
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas ?
Solution:
Let R and r be the radii of two circles, then the ratio between their circumferences = 2πR : 2πr
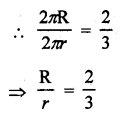
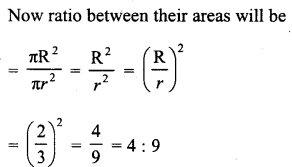
Question 3.
Write the area of the sector of a circle whose radius is r and length of the arc is l.
Solution:
Let arc l subtends angle 9 at the centre of the circle
Now radius of a circle = r
and length of arc =l
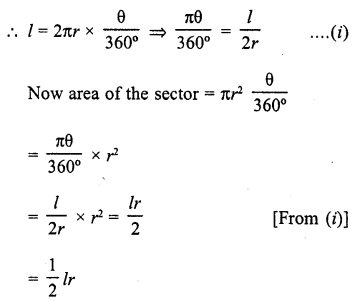
Question 4.
What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
Solution:
Radius of the circle = 5 cm
Angle at the center = 36°
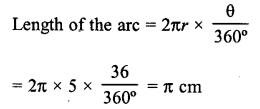
Question 5.
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3π cm ?
Solution:
Let the arc subtends angle θ at the centre of a circle
Radius of circle (r) = 6 cm
Length of arc = 3π cm
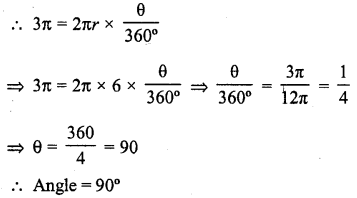
Question 6.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm ?
Solution:
Radius of the circle (r) = 5 cm
Length of arc (l) = 3.5 cm
Let angle 9 be subtended by the arc at the centre
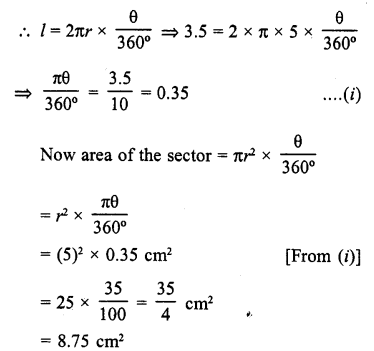
Question 7.
In a circle of radius 10 cm, an arc subtends an angle of 108° at the centre. What is the area of the sector in terms of π ?
Solution:
Radius of the circle = 10 cm
Angle at the centre = 108°

Question 8.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square ?
Solution:
A square ABCD is inscribed in a circle with centre O
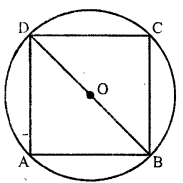
Let the radius of the circle = r
Then its area = πr²
Now diagonal of the square = diameter of the circle = 2r
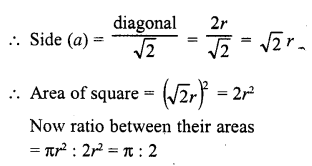
Question 9.
Write the formula for the area of a sector of angle θ (in degrees) of a circle of radius r.
Solution:
Area of a sector of a circle whose radius = r
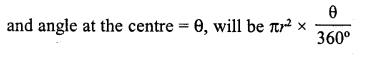
Question 10.
Write the formula for the area of a segment in a circle of radius r given that the sector angle is 0 (in degrees).
Solution:
Radius of the circle = r
and angle subtended by the sector at the centre = θ
Area of the segment
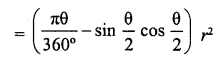
Question 11.
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector ? (Take π= 22/7)
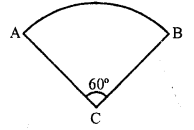
Solution:
Radius of the circle = 10.5 cm
Angle at the centre of the circle = 60°

Question 12.
If the diameter of a semi-circular protractor is 14 cm then find its perimeter. (C.B.S.E. 2009)
Solution:
Diameter of semicircular protractor = 14 cm
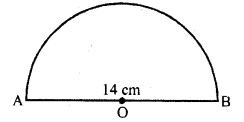
∴ Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm
Now perimeter of protractor
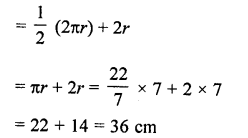
Question 13.
An arc subtends an angle of 90° at the centre of the circle of radius 14 cm. Write the area of minor sector thus formed in terms of π.
Solution:
AB is an arc of the circle with centre O and radius 14 cm and subtends an angle of 90° at the centre O.
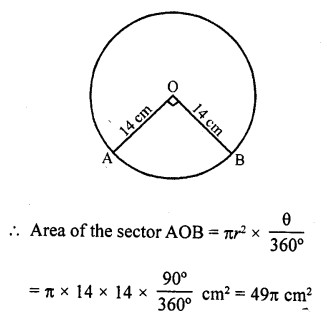
Question 14.
Find the area of the largest triangle that can be inscribed in a semi-circle of radius r units. [CBSE 2015]
Solution:
Radius of semicircle = r
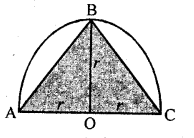
In semicircle ΔABC is the largest triangle whose base is AC = 2 x r = 2r units
and height OB = r units
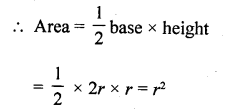
Question 15.
Find the area of a sector of circle of radius 21 cm and central angle 120°.
Solution:
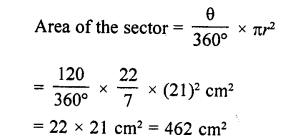
Question 16.
What is the area of a square inscribed in a circle of diameter p cm?
Solution:
Diameter AC of the circle is p.
Also AC is diagonal of square ABCD.
Each angle of square is of 90°
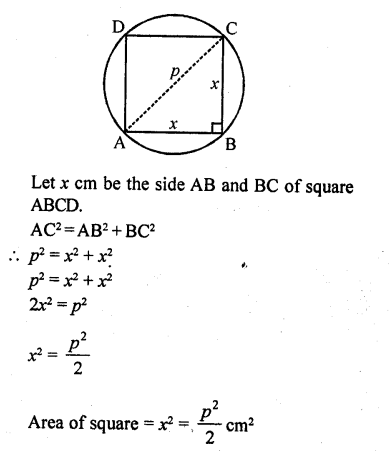
Question 17.
Is it true to say that area of a segment of a circle is less than the area of its corresponding sector? Why?
Solution:
False.
It is true only in the case of minor segment. But in case of major segment, area is always greater than the area of sector.
Question 18.
If the numerical value of the area of a circle is equal to the numerical value of its circumference, find its radius.
Solution:
∵ Numerical value of area of circle = Numerical value of circumference
∴ πr² = 2πr
or r = 2 units
Question 19.
How many revolutions a circular wheel of radius r metres makes in covering a distance of s metres?
Solution:
Radius of circular of wheel (r) = r m
Circumference of a circular wheel = 2πr
Distance to be covered = Sm
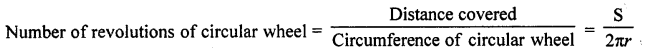
Question 20.
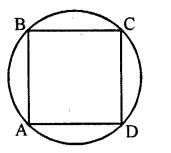
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square.
Solution:
Let each side of of square = x
∴ Diameter of inner circle = x
Radius r = \(\frac { x }{ 2 }\)
Diameter of outer circle = AD
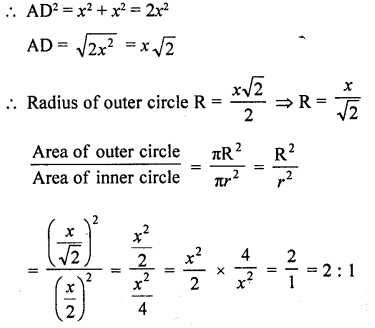
Hope given RD Sharma Class 10 Solutions Chapter 13 Areas Related to Circles VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.