RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
Other Exercises
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
- RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS
Question 1.
Find the L.C.M. and H.C.F. of the following pairs of integers and verify that L.C.M. x H.C.F. = Product of the integers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
(i) 26 and 91
26 = 2 x 13
91 = 7 x 13
H.C.F. = 13
and L.C.M. = 2 x 7 x 13 = 182
Now, L.C.M. x H.C.F. = 182 x 13 = 2366
and 26 x 91 = 2366
L.C.M. x H.C.F. = Product of integers
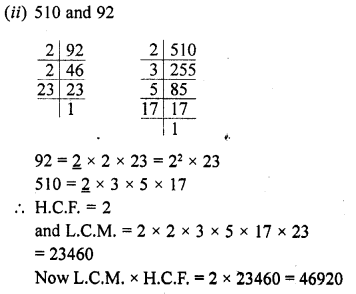

Question 2.
Find the L.C.M. and H.C.F. of the following integers by applying the prime factorisation method :
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
(iv) 40, 36 and 126
(v) 84, 90 and 120
(vi) 24,15 and 36
Solution:



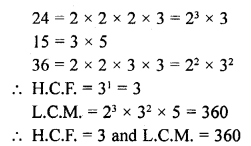
Question 3.
Given that HCF (306, 657) = 9, Find LCM (306, 657). [NCERT]
Solution:
HCF of 306, 657 = 9

Question 4.
Can two numbers have 16 as their H.C.F. and 380 as their L.C.M. ? Give reason.
Solution:
H.C.F. of two numbers = 16
and their L.C.M. = 380
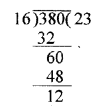
We know the H.C.F. of two numbers is a factor of their L.C.M. but 16 is not a factor of 380 or 380 is not divisible by 16
It can not be possible.
Question 5.
The H.C.F. of two numbers is 145 and their L.C.M. is 2175. If one number is 725, find the other.
Solution:
First number = 725
Let second number = x
Their H.C.F. = 145
and L.C.M. = 2175

Second number = 435
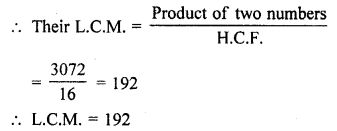
Question 6.
The H.C.F. of two numbers is 16 and their product is 3072. Find their L.C.M.
Solution:
H.C.F. of two numbers = 16
and product of two numbers = 3072
Question 7.
The L.C.M. and H.C.F. of two numbers are 180 and 6 respectively. If one of the number is 30, find the other number.
Solution:
First number = 30
Let x be the second number
Their L.C.M. = 180 and H.C.F. = 6
We know that
first number x second number = L.C.M. x H.C.F.
30 x x = 180 x 6
⇒ x = \(\frac { 180\times 6 }{ 30 }\) = 36
Second number = 36
Question 8.
Find the smallest number which when increased by 17 is exactly divisible by both 520 and 468.
Solution:
L.C.M. of 520 and 468

= 2 x 2 x 9 x 10 x 13 = 4680
The number which is increased = 17
Required number 4680 – 17 = 4663
Question 9.
Find the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
Solution:
Dividing by 28 and 32, the remainders are 8 and 12 respectively
28 – 8 = 20
32 – 12 = 20
Common difference = 20
Now, L.C.M. of 28 and 32
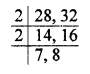
= 2 x 2 x 7 x 8 = 224
Required smallest number = 224 – 20 = 204
Question 10.
What is the smallest number that, when divided by 35, 56 and 91 leaves remainders of 7 in each case ?
Solution:
L.C.M. of 35, 56, 91
![]()
= 5 x 7 x 8 x 13 = 3640
Remainder in each case = 7
The required smallest number = 3640 + 7 = 3647
Question 11.
A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. It is to be paved with square tiles of same size. Find the least possible number of such tiles.
Solution:
Length of rectangle = 18 m 72 cm = 1872 cm
and breadth = 13 m 20 cm = 1320 cm
Side of the greatest size of square tile = H.C.F. of 1872 and 1320
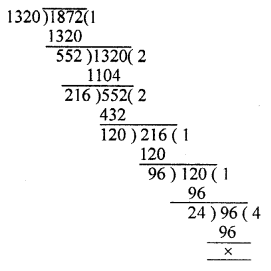

Question 12.
Find the greatest number of 6 digits exactly divisible by 24, 15 and 36.
Solution:
Greatest number of 6 digits = 999999
Now L.C.M. of 24, 15 and 36

We get quotient = 2777
and remainder = 279
Required number = 999999 – 279 = 999720
Question 13.
Determine the number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
Solution:

Required number will be = 110000 – 800 =109200
Question 14.
Find the least number that is divisible by ail the numbers between 1 to 10 (both inclusive).
Solution:
The required least number which is divisible by 1 to 10 will be the L.C.M. of 1 to 10
L.C.M. of 1 to 10

Question 15.
A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48, 60 and 72 km a day, round the field. When will they meet again ?
Solution:
Circumference of a circular field = 360 km
Three cyclist start together who can cycle 48, 60 and 72 km per day round the field
L.C.M. of 48, 60, 72
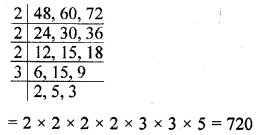
They will meet again after 720 km distance
Question 16.
In a morning walk, three persons step off together, their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that they can cover the distance in complete steps ?
Solution:
Measures of steps of three persons = 80 cm, 85 cm and 90 cm
Minimum required distance covered by them = L.C.M. of 80 cm, 85 cm, 90 cm

= 2 x 5 x 8 x 9 x 17
= 12240 cm
= 122.40 m
= 122 m 40 cm
Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.