Here we are providing Probability Class 9 Extra Questions Maths Chapter 15 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers.
Extra Questions for Class 9 Maths Probability with Answers Solutions
Extra Questions for Class 9 Maths Chapter 15 Probability with Solutions Answers
Probability Class 9 Extra Questions Very Short Answer Type
Question 1.
The blood groups of some students of Class IX were surveyed and recorded as below :
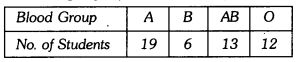
If a student is chosen at random, find the probability that he/she has blood group A or AB.
Solution:
Here,
total number of students = 19 + 6 + 13 + 12 = 50
Number of students has blood group A or AB = 19 + 13 = 32
Required probability = \(\frac{38}{50}\) = \(\frac{16}{25}\)
Question 2.
A group of 80 students of Class X are selected and asked for their choice of subject to be
taken in Class XI, which is recorded as below :

If a student is chosen at random, find the probability that he/she is a student of either commerce or humanities stream.
Solution:
Here, total number of students = 80
Total number of students of Commerce or Humanities stream = 33
Required probability = \(\frac{33}{80}\)
Question 3.
A box contains 50 bolts and 150 nuts. On checking the box, it was found that half of the bolts and half of the nuts are rusted. If one item is chosen at random, find the probability that it is rusted.
Solution:
Total number of nuts and bolts in the box = 150 + 50
= 200
Number of nuts and bolts rusted = \(\frac{1}{2}\) × 200 = 100
P(a rusted nut or bolt) = \(\frac{100}{200}\) = \(\frac{1}{2}\)
Question 4.
A dice is rolled number of times and its outcomes are recorded as below:

Find the probability of getting an odd number.
Solution:
Total number of outcomes = 250
Total number of outcomes of getting odd numbers = 35 + 50 + 53 = 138
∴ P(getting an odd number) = \(\frac{138}{250}\) = \(\frac{69}{125}\)
Question 5.
The probability of guessing the correct answer to a certain question is \(\frac{x}{2}\) If probability of
not guessing the correct answer is \(\frac{2}{3}\), then find x.
Solution:
Here, probability of guessing the correct answer = \(\frac{x}{2}\)
And probability of not guessing the correct answer = \(\frac{x}{2}\)
Now, \(\frac{x}{2}\) + \(\frac{2}{3}\) = 1
⇒ 3x + 4 = 6
⇒ 3x = 2
⇒ x = \(\frac{2}{3}\)
Question 6.
A bag contains x white, y red and z blue balls. A ball is drawn at the random, then what is the probability of drawing a blue ball.
Solution:
Number of blue balls = Z
Total balls = x + y + Z
∴ P(a blue ball) = \(\frac{z}{x+y+z}\)
Probability Class 9 Extra Questions Short Answer Type 1
Question 1.
750 families with 3 children were selected randomly and the following data recorded:

If a family member is chosen at random, compute the probability that it has :
(i) no boy child
(ii) no girl child
Solution:
(i) P(no boy child) = \(\frac{100}{750}\) = \(\frac{2}{15}\)
and P (no girl child) = \(\frac{120}{750}\) = \(\frac{4}{25}\)
Question 2.
If the probability of winning a race of an athlete is \(\frac{1}{6}\) less than the twice the probability of losing the race. Find the probability of winning the race.
Solution:
Let probability of winning the race be p
∴ Probability of losing the race = 1 – p
According to the statement of question, we have
p = 2 (1 – p) – \(\frac{1}{6}\)
⇒ 6p = 12 – 12p – 1
⇒ 18p = 11
⇒ p = \(\frac{11}{18}\) .
Hence, probability of winning the race is \(\frac{11}{18}\).
Question 3.
Three coins are tossed simultaneously 150 times with the following frequencies of different outcomes :

Compute the probability of getting :
(i) At least 2 tails
(ii) Exactly one tail
Solution:
Here, total number of chances = 150
(i) Total number of chances having at least 2 tails = 32 + 63 = 95
∴ Required probability = \(\frac{95}{150}\) = \(\frac{19}{30}\)
(ii) Total number of chances having exactly one tail = 30
∴ Required probability = \(\frac{30}{150}\) = \(\frac{1}{5}\)
Probability Class 9 Extra Questions Short Answer Type 2
Question 1.
The table shows the marks obtained by a student in unit tests out of 50 :

Find the probability that the student get 70% or more in the next unit test. Also, the probability that student get less than 70%.
Solution:
Here, the marks are out of 50, so we first find its percentage (i.e., out of 100)

Total number of outcomes = 5
Probability of getting 70% or more marks = \(\frac{3}{5}\)
Probability of getting less than 70% = \(\frac{2}{5}\)
Question 2.
Books are packed in piles each containing 20 books. Thirty five piles were examined for defective books and the results are given in the following table :

One pile was selected at random. What is the probability that it has :
(i) no defective books ?
(ii) more than 0 but less than 4 defective books ?
(iii) more than 4 defective books ?
Solution:
Total number of books = 700
(i) P(no defective books) = \(\frac{400}{700}\) = \(\frac{4}{7}\)
(ii) P(more than 0 but less than 4 defective books) = \(\frac{269}{700}\)
13 (iii) P(more than 4 defective books) = \(\frac{13}{700}\)
Probability Class 9 Extra Questions Short Answer Type 1 and 2
Question 1.
Two coins are tossed simultaneously for 360 times. The number of times ‘2 Tails’ appeared was three times ‘No Tail’ appeared and number of times ‘1 Tail’ appeared is double the number of times ‘No Tail’ appeared. Find the probability of getting ‘Two tails’.
Solution:
Total number of outcomes = 360
Let the number of times ‘No Tail’ appeared be x
Then, number of times 2 Tails’ appeared = 3x
Number of times ‘1 Tail’ appeared = 2x
Now, x + 2x + 3x = 360
⇒ 6x = 360
⇒ x = 60
P(of getting two tails) = \(\frac{3 \times 60}{360}\) = \(\frac{1}{2}\)
Question 2.
A die was rolled 100 times and the number of times, 6 came up was noted. If the experimental probability calculated from this information is \(\frac{2}{5}\), then how many times 6 came up ? Justify your answer.
Solution:
Here, total number of trials = 100
Let x be the number of times occuring 6.
We know, probability of an event
= \(\frac { Frequency\quad of\quad the\quad event\quad occuring }{ Total\quad number\quad of\quad trails }\)
⇒ \(\frac{x}{100}\) = \(\frac{2}{5}\) [∵ Probability is given)
⇒ x = 40
Probability Class 9 Extra Questions Long Answer Type
Question 1.
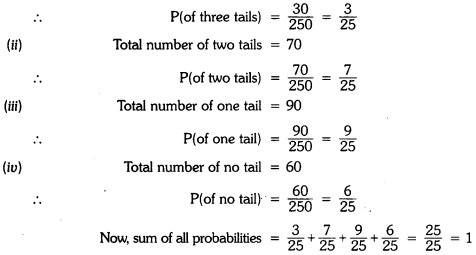
Three coins are tossed simultaneously 250 times. The distribution of various outcomes is listed below :
(i) Three tails : 30,
(ii) Two tails : 70,
(iii) One tail : 90,
(iv) No tail : 60
Find the respective probability of each event and check that the sum of all probabilities is 1.
Solution:
Here, the total number of chances = 250
Total number of three tails = 30
Question 2.
A travel company has 100 drivers for driving buses to various tourist destination. Given
below is a table showing the resting time of the drivers after covering a certain distance (in km).

What is the probability that the driver was chosen at random :
(a) takes a halt after covering 80 km?
(b) takes a halt after covering 115 km?
(c) takes a halt after covering 155 km?
(d) takes a halt after crossing 200 km?
Solution:
Total number of drivers = 100
(a) P (takes a halt after covering 80 km) = \(\frac{13}{100}\)
(b) P (takes a halt after covering 115 km) = \(\frac{60}{100}\) = \(\frac{3}{5}\)
(c) P (takes a halt after covering 155 km) = \(\frac{90}{100}\) = \(\frac{9}{10}\)
(d) P (takes a halt after crossing 200 km) = \(\frac{10}{100}\) = \(\frac{1}{10}\)
Question 3.
A company selected 2300 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a home. The information gathered is listed in the table below :
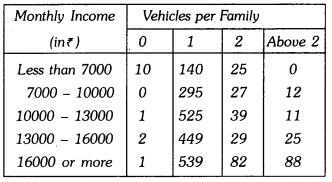
If a family is chosen at random, find the probability that the family is :
(i) earning ₹7000 – ₹13000 per month and owning exactly 1 vehicle.
(ii) owning not more than one vehicle. (iii) earning more than ₹13000 and owning 2 or more than 2 vehicles. (iv) owning no vehicle
Solution:
Here, we have a total number of families = 2300
(i) Number of families earning ₹7000 to ₹13000 per month and owning exactly 1 vehicle = 295 + 525 = 820

Question 4.
A survey of 2000 people of different age groups was conducted to find out their preference
in watching different types of movies :
Type I + Family Type II → Comedy and Family
Type III → Romantic, Comedy, and Family 242.
Type IV → Action, Romantic, Comedy and Family

Find the probability that a person chosen at random is :
(a) in 18-29 years of age and likes type II movies
(b) above 50 years of age and likes all types of movies
(c) in 30-50 years and likes type I movies. :
Solution:
(a) Let E1 be the event, between the age group (18 – 29) years and liking type II movies
Favourable outcomes to event E1 = 160
∴ P(E1) = \(\frac{160}{2000}\) = \(\frac{160}{2000}\)
(b) Let E2 be the event, of age group above 50 years and like all types of movies
Favourable outcomes to event E2 = 9
∴ P(E2) = \(\frac{9}{2000}\)
(c) Let E3 be the event, between age group (30 – 50) years and liking type I movies
Favourable outcomes to event E3 = 505
∴ P(E3) = \(\frac{505}{2000}\) = \(\frac{101}{400}\)
Probability Class 9 Extra Questions HOTS
Question 1.
In a kitchen, there are 108 utensils, consisting of bowls, plates, and glasses. The ratio of bowls, plates the glasses is 4:2:3. A utensil is picked at random. Find the probability that :
(i) it is a plate.
(ii) it is not a bowl.
Solution:
Total utensils in the kitchen = 108
Let number of bowls be 4x, number of plates be 2x and number of glasses be 3x
∴ 4x + 2x + 3x = 108
9x = 108
x = \(\frac{108}{9}\) = 12
Thus, number of bowls = 4 × 12 = 48
Number of plates = 2 × 12 = 24
Number of glasses = 3 × 12 =
(i)P (a plate) = \(\frac{24}{108}\) = \(\frac{2}{9}\)
(ii) P (not a bowl) = \(\frac{24+36}{108}\) = \(\frac{60}{108}\) = \(\frac{5}{9}\)
Question 2.
A bag contains 20 balls out of which x are white.
(a) If one ball is drawn at random, find the probability that it is white.
(b) If 10 more white balls are put in the bag, the probability of drawing a white ball will be double that in part (a), find x.
Solution:
Here, total no. of balls = 20
No. of white balls = x
∴ P(white ball) = \(\frac{x}{20}\)
Now, 10 more white balls are added
∴ Total no. of balls = 20 + 10 = 30
Total no. of white balls = x + 10
According to statement of question, we have
\(\frac{x+10}{30}\) = 2 × \(\frac{x}{20}\)
⇒ \(\frac{x+10}{3}\) = x
⇒ x + 10 = 3x
⇒ 2x = 10
⇒ x = 5
Question 3.
Here is an extract from a mortality table.
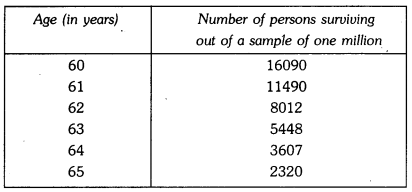
(i) Based on this information, what is the probability of a person aged 60′ of dying within a year ?
(ii) What is the probability that a person aged 61′ will live for 4 years ?
Solution:
(i) Clearly 16090 persons aged 60, (16090 – 11490), i.e., 4600 died before reaching their 61st birthday.
Therefore, P (a person aged 60 die within a year) = \(\frac{4600}{16090}\) = \(\frac{460}{1609}\)
(ii) Number of persons aged 61 years = 11490
Number of persons surviving for 4 years = 2320
P (a person aged 61 will live for 4 years) = \(\frac{2320}{11490}\) = \(\frac{232}{1149}\)
Probability Class 9 Extra Questions Value Based (VBQs)
Question 1.
An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained are given in the following table :
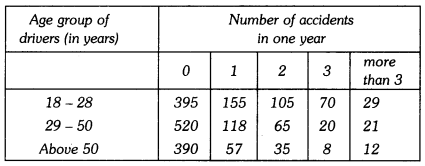
Find the probability of the following events for a driver-selected at random from the city :
(i) being 18 – 29 years of age and having exactly 3 accidents in one year.
(ii) being 30 – 50 years of age and having one or more accidents in a year.
(iii) having no accident in one year.
(iv) Which value would you like to remember from this data?
Solution:
Here, total number of drivers = 2000
(i) The number of drivers in the age group 18 – 29 having exactly 3 accidents = 70
So, P (driver in age group 18 – 29 having exactly 3 accidents in one year) = \(\frac{70}{2000}\) = 0.035
(ii). The number of drivers in the age group 30 – 50 and having one or more than one accidents in one year = 118 + 65 + 20 + 21 = 224
P (driver in age group 30 – 50 having one or more accidents in one year) = \(\frac{224}{2000}\) = 0.112
(iii) The number of drivers having no accident in one year = 395 + 520 + 390 = 1305
So, P (driver having no accident) = \(\frac{1305}{2000}\) = 0.6525
(iv) Most people in India died or injured due to accidents as compared to any other country. So, we should obey the traffic rules as life is very precious.
Question 2.
100 plants were sown in six different colonies A, B, C, D, E, and F. After 31 days, the number of plants survived as follows :

What is the probability of :
(i) more than 80 plants survived in a colony?
(ii) less than 82 plants survived in a colony?
(iii) which values are depicted from the above data?
Solution:
Here, we have total number of colonies = 6
(i) Number of colonies in which more than 80 plants survived = 4 (i.e., B, C, E and F)
∴ P(more than 80 plants survived in a colony) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
(ii) Number of colonies in which less than 82 plants survived = 2 (i.e., A and D)
∴ P (less than 82 plants survived in a colony) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
(iii) In order to keep environment safe, clean and green, we should grow more and more plants.