Students rely on Class 6 Maths Extra Questions Chapter 5 Prime Time Class 6 Extra Questions and Answers to improve their grades.
Class 6 Maths Chapter 5 Extra Questions Prime Time
Class 6 Maths Prime Time Extra Questions
NCERT Class 6 Maths Chapter 5 Prime Time Extra Questions and Answers
Very Short Answer Type Questions
Question 1.
Write the first three multiples of each of the following
(i) 11
(ii) 12
Answer:
(i) First three multiples of 11 = 11, 22, 33
(ii) First three multiples of 12 = 12, 24, 36
Question 2.
Write the greatest and the smallest prime number between 10 and 20.
Answer:
Greatest prime number = 19
Smallest prime number =11
Question 3.
Write all the prime numbers between
(i) 10 and 15
(ii) 20 and 35
Answer:
(i) Prime numbers between 10 and 15 = 11, 13
(ii) Prime numbers between 20 and 35 = 23, 29, 31
Question 4.
Which of the following are composite numbers?
7, 13, 16
Answer:
Given numbers are 7,13,16.
Factors of 7 = 1,7
Factors of 13 = 1,13 Factors of 16 = 1, 2, 4, 8, 16
∴ 16 is a composite number.
Question 5.
Write the common factors of 6 and 10.
Answer:
Factors of 6 = 1, 2, 3, 6
Factors of 10 = 1, 2, 5, 10
Common factors of 6 and 10 = 1 and 2
Question 6.
Write the highest common factor of 6 and 15.
Answer:
Factors of 6 = 1, 2, 3, 6
Factors of 15 = 1, 3, 5, 15
Common factors = 1 and 3
Highest common factor = 3
Question 7.
Write the first two common multiples of 5 and 15.
Answer:
Multiples of 5 = 5, 10, 15, 20, 25, 30,…
Multiples of 15 = 15, 30,…
First two common multiples = 15 and 30
![]()
Question 8.
Find the prime factorisation of 40.
Answer:
Here, we have 40

40 = 2 × 2 × 2 × 5
Short Answer Type Questions
Question 1.
Give the factorisation of the following numbers.
(i) 136
(ii) 252
Answer:
(i) We have, 136

∴ 136 = 2 × 2 × 2 × 17
(ii) We have, 252

∴ 252 = 2 × 2 × 3 × 3 × 7
Question 2.
Is 12 and 25 are coprime?
Answer:
Yes, they are coprime because they have no common factors other than 1.
Question 3.
Find the common factors of 12 and 18.
Answer:
The common factors of 12 and 18 are 1, 2, 3 and 6.
Question 4.
Is 51 a composite number?
Answer:
Yes, 51 is a composite number because it has factors other than 1 and itself.
Specifically, 51 can be divided by 1, 3, 17 and 51.
Question 5.
Find the prime factorisation of 1600.
Answer:
Prime factorisation of 1600.
1600 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5
Question 6.
What is the test of divisibility for 2?
Answer:
A number is divisible by 2 if its last digit is 0, 2,4, 6 or 8.
Question 7.
Is 72 divisible by 4?
Answer:
Yes, because the last two digits (72) form a number divisible by 4.
Question 8.
Use prime factorisation to check if 2520 and 3003 are
Answer:
Prime factorisation of 2520 and 3003.
2520 = 2 × 2 × 2 × 3 × 3 × 5 × 7
3003 = 3 × 7 × 11 × 13
The common prime factors of 2520 and 3003 are 3 and 7.
Since, they have common prime factors (3 and 7), therefore 2520 and 3003 are not coprime.
Long Answer Type Questions
Question 1.
Find a 4-digit odd number using each of digits 1,2,4 and 5 only once such that when the first and last digits are interchanged, it is divisible by 4.
Answer:
The 4-digit number will be an odd number, if the unit place digit is an odd number (i.e. 1 or 5).
Total such odd numbers are
4125, 4215, 1245, 1425, 2145, 2415, 4251, 4521, 5241, 5421,2451,2541.
Also, we know that any 4-digit number is divisible by 4, if the last two-digit number is divisible by 4.
Consider a number 4521, if we interchage the first and the last digit, the new number will be 1524.
Here, we see that the last two digits (i.e. 24) is divisible by 4.
So, the number 1524 is divisible by 4.
Similarly, other numbers when we interchange the first and the last digit, divisible by 4 are 4125, 2415, 2451.
Hence, the required 4-digit numbers are 4521, 4125, 2415 and 2451.
Question 2.
Find the common prime factors of 120 and 84 and determine if they have any common factors other than 1.
Answer:
Prime factorisation of 120 and 84.
120 = 2 × 2 × 2 × 3 × 5
84 = 2 × 2 × 3 × 7
The common prime factors are 2 and 3.
The common factors other than 1 are 2, 3, 4, 6 and 12.
![]()
Question 3.
Identify whether the following numbers are prime or composite : 29, 56, 101 and 77.
For each number provide a brief explanation of why it is classified as prime or composite.
Answer:
For 29, the only divisors are 1 and 29.
Thus, 29 is a prime number.
For 56, the divisors are 1, 2, 4, 7, 8, 14, 28 and 56.
Therefore, 56 is a composite number.
For 101, Since it is not divisible by 2, 3, 5 or 7, it has no divisors other than 1.
Thus, 101 is a prime number.
For 77, it can be divided by 1, 7, 11 and 77.
So, it has other divisors other than 1 and itself.
Therefore, 77 is composite numbers.
Question 4.
Check if the following numbers are divisible by 2, 4 and 5 :144, 250 and 341. For each number, explain how you determine its divisibility by these numbers.
Answer:
For 144
The last digit is 4, therefore 144 is divisible by 2.
The number formed by last two digits (44) is divisible by 4, therefore 144 is divisible by 4.
The last digit is not 0 or 5 , .. therefore 144 is not divisible by 5.
For 250
The last digit is 0, therefore it is divisible by 2.
The number formed by last two digits (50) is not divisible by 4, therefore 144 is not divisible by 4.
The last digit is 0, therefore 144 is divisible by 5.
For 341
The last digit is 1, therefore it is not divisible by 2.
The number formed by last two digits (41) is not divisible by 4, therefore 341 is not divisible by 4.
The last digit is not 0 or 5, therefore 341 is not divisible by 5.
Case-Based Questions
Question 1.
A photographer is hired to take group photographs of students in each class in a school. He arranges the students along with teachers in rows for the photograph. His arrangement has
- atmost 50 people.
- an equal number of people in each row.
A row consists of a minimum of 3 people and a maximum of 8 people.
(i) There are 35 people (students and teachers) in a class for a group photograph. What are the possible arrangements for them?
Answer:
Total number of people (students and teachers) = 35
Factors of 35 are 1, 5, 7 and 35.
Hence, possible arrangements
= 7 rows and 5 students/teachers per row or 5 rows and 7 students/teachers per row
(ii) The photographer arranged some of the students in 6 rows. What can be the maximum number of students in the photograph?
(a) 18
(b) 36
(c) 48
(d) 60
Answer:
(c) The photographer arranged students in 6 rows. Given, maximum number of people in a row = 8
.’. Maximum number of students = 6 x 8 = 48
(iii) How did the students of Class 7 which are 30 in number want to take a photograph along with 2 teachers. Which of the following is the possible arrangement for them?
(a) 2 rows with 16 students in each.
(b) 4 rows with 8 students/teachers in each.
(c) 5 rows with 6 students in each and 1 row for teachers.
Answer:
(b) There are 30 students and 2 teachers in class 7. Thus, in total 32 people.
Let us consider maximum people in a row i.e. 8.
So, divide 32 by 8 to know the number of rows.
32 ÷ 8 = 4
Hence, 4 rows with 8 students/teachers in each.
![]()
Question 2.
Ananya is exploring divisibility rules using prime factorisation. She needs to check which numbers are divisible by 12 and 15.
To do this, she first needs to find the prime factorisation of 12 and 15.
Based on the above information, answer the following questions.
(i) What are the prime factors of 12 and 15?
Answer:
Prime factorisation of 12 and 15. s
12 = 2 × 2 × 3
15 = 3 × 5
(ii) Determine of 60 and 90 are divisible by both 12 and 15 using prime factorisation.
Answer:
Prime factorisation of 60 and 90.
60 = 2 × 2 × 3 × 5
90 = 2 × 3 × 3 × 5
So, 60 = 12 × 5 and 60 = 4 × 15
Thus, 60 is divisible by both 12 and 15.
And 90 = 6 × 15
Thus, 90 is divisible by 15 but not 12.
![]()
Skill Based Questions
Question 1.
A Prime Puzzle
The figure on the left shows the puzzle. The figure on the right shows the solution of the puzzle. Think what rules can be to solve the puzzle.
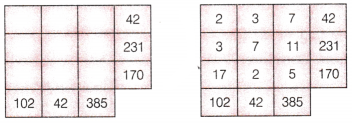
Answer:
The rule to solve the puzzle is as follow :
Grid is filled with prime number only so that the product of each row is the number to the right of the row and the product of each column is the number is mentioned below the column.
Question 2.
Solve the following crossword puzzle.

Across
1. Every number is a factor of ………
4. Number which have more than two factors is called ……… numbers.
7. Numbers which have exactly two factors, 1 and the number itself is called …….. numbers.
Down
2. An exact divisor of a number is called …….
3. By multiplying a number by a natural number, we get a ……… of that number.
5. ………. is neither prime nor composite.
6. The smallest natural number is …………
Answer:
2. Across
1. Itself
2. Composite
7. Prime
Down
2. Factor
3. Multiple
5. One
6. One
Class 6 Maths Chapter 5 Extra Questions in Hindi अभाज्य समय
Prime Time Class 6 Extra Questions in Hindi
उदाहरण 1.
प्रथम तीन सार्व गुणज ज्ञात कीजिए।
(a) 6 और 8
(b) 12 और 18
हल:
(a) दी गई संख्याएँ 6 और 8 हैं।
6 के पहले कुछ गुणज हैं – 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78….
इस प्रकार, 8 के गुणज हैं- 8, 16, 24, 32, 40, 48, 56, 64, 72, 80…
अतः 6 और 8 के प्रथम तीन सार्व गुणज 24, 48 और 72 हैं।
(b) दी गई संख्याएँ 12 और 18 हैं। 12 के पहले कुछ गुणज हैं 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …..
इसी प्रकार 18 के गुणज हैं 18, 36, 54, 72, 90, 108, 126, ……
अतः 12 और 18 के प्रथम तीन सार्व गुणज 36, 72 और 108 हैं।
उदाहरण 2.
निम्नलिखित के सार्व गुणनखंड ज्ञांत कीजिए।
(a) 20 और 28
(b) 15 और 25
(d) 56 और 120
(c) 35 और 50
हल:
(a) 20 के गुणनखंड 1, 2, 4, 5, 10, 20 हैं।
28 के गुणनखंड 1, 2, 4, 7, 28 हैं। इसलिए 20 और 28 के सार्व गुणनखंड 1, 2 और 4 हैं।
(b) 15 के गुणनखंड 1, 3, 5, 15 हैं।
25 के गुणनखंड 1, 5, 25 हैं। इसलिए 15 और 25 के सार्व गुणनखंड 1 और 5 हैं।
(c) 35 के गुणनखंड 1, 5, 7, 35 हैं। 50 के गुणनखंड 1, 2, 5, 10, 50 है। इसलिए, 35 और 50 के सार्व गुणनखंड 1 और 5 हैं।
(d) 56 के गुणनखंड 1, 2, 4, 7, 8, 14, 28, 56 हैं। 120 के गुणनखंड 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120 हैं। इसलिए 56 और 120 के सार्व गुणनखंड 1, 2, 4 और 8 हैं।
उदाहरण 3.
निम्नलिखित में से कौन-सी भाज्य संख्या है?
(a) 81
(b) 37
(c ) 17
(d) 19
हल:
यहाँ
(a) 81 = 1 × 81 = 3 × 27 = 9 × 9
(b) 37 = 1 × 37
(c ) 17 = 1 × 17
(d) 19 = 1 × 19
चूँकि 81 के दो से अधिक गुणनखंड अर्थात् 1, 3, 9, 27, 81 हैं। इसलिए 81 एक भाज्य संख्या है, जबकि 37, 17 और 19 अभाज्य संख्याएँ हैं।
अत: विकल्प (a) सही है।
उदाहरण 4.
ज्ञात कीजिए कि क्या संख्या 53 एक अभाज्य संख्या है या नहीं
हलः
53 के गुणनखंड 1 और 53 हैं।
संख्या 53 केवल दो संख्याओं 1 और स्वयं से विभाजित होती है। इसलिए, 53 एक अभाज्य संख्या है।
![]()
उदाहरण 3.
अभाज्य संख्याओं के तीन युग्म लिखिए जिनका अंतर 2 हो, अर्थात अभाज्य युग्म हो।
हलः
तीन युग्म ( 3, 5), (5, 7) और (11, 13) हैं
उदाहरण 4.
निम्नलिखित में से कौन-सी संख्या सह-अभाग्य हैं?
(a) 8, 10
(b) 9, 10
(c) 6, 8
(d) 15, 18
हल:
(a) 8 = 1 × 2 × 2 × 2
10 = 1 × 2 × 5
2, 1 के अलावा एक सार्व गुणनखंड है।
(b) 9 = 1 × 3 × 3
10 = 1 × 2 × 5
1 के अलावा कोई सार्व गुणनखंड नहीं है।
(c) 6 = 1 × 2 × 3
8 = 1 × 2 × 2 × 2
2, 1 के अलावा एक सार्व गुणनखंड है।
(d) 15 = 1 × 3 × 5
18 = 1 × 3 × 3 × 2
3, 1 के अलावा सार्व गुणनखंड है।
अत: (9, 10) सहअभाज्य हैं क्योंकि 1 के अलावा कोई सार्व गुणनखंड नहीं हैं। इसलिए, विकल्प (b) सही है।
उदाहरण 5.
चार अंकों की सबसे बड़ी संख्या लिखें और इसका अभाज्य गुणनखंडन करें।
हल:
चार अंकों की सबसे बड़ी संख्या 9999
हम जानते हैं

चार अंकों की सबसे बड़ी संख्या 9999 है और इसे 3 × 3 × 11 × 101 रूप में व्यक्त किया जा सकता है।
उदाहरण 6.
जाँच कीजिए क्या 195, 4 से विभाज्य है या नहीं?
हल:
यहाँ 195 का अंतिम अंक 5 है जो 4 से विभाज्य नहीं है।
अतः 195, 4 से विभाज्य नहीं है।
उदाहरण 7.
निम्नलिखित में से कौन-से कथन सत्य हैं?
(i) यदि कोई संख्या 3 से विभाज्य है तब वह 9 से भी विभाज्य होती है।
(ii) यदि कोई संख्या 9 से विभाज्य है तब वह 3 से भी विभाज्य होती है।
(iii) यदि कोई संख्या 4 से विभाज्य है तब वह 8 से भी विभाज्य होती है।
(iv) यदि कोई संख्या 8 से विभाज्य है तब वह 4 से विभाज्य होती है।
(v) यदि कोई संख्या 18 से विभाज्य है तब वह 3 और 6 दोनों से विभाज्य होती है।
(vi) यदि कोई संख्या 9 और 10 दोनों से विभाज्य है तब वह 90 से भी विभाज्य होती है।
(vii) यदि कोई संख्या दो संख्याओं के योग को पूर्णत: विभाजित करती है तो वह संख्या उन दोनों संख्याओं को अलग-अलग भी विभाजित करती है।
(viii) यदि कोई संख्या तीन संख्याओं को विभाजित करती है तो उसे उनकी योग को ठीक से विभाजित करना चाहिए।
(ix) यदि दो संख्याएँ सह अभाज्य है तो उनमें से कम से कम एक अभाज्य संख्या होती है।
(x) दो क्रमागत विषम संख्याओं का योग हमेशा 4 से विभाज्य होता है।
हल:
(i) असत्य संख्या 15, 3 से विभाज्य है लेकिन 9 से विभाज्य नहीं है।
(ii) सत्य संख्या 18, 9 और 3 दोनों से विभाज्य है।
(iii) असत्य संख्या 12, 4 से विभाज्य है परन्तु 8 से विभाज्य नहीं है।
(iv) सत्य संख्या 16 8 और 4 दोनों से विभाज्य है।
(v) असत्य संख्या 24, 3 और 6 दोनों से विभाज्य है परन्तु 18 से विभाज्य नहीं है।
(vi) सत्य 90, 9 और 10 दोनों से विभाज्य है।
(vii) असत्य 18 और 2 का योग संख्या 10 से विभाज्य है परन्तु 10 न तो 18 को नहीं 2 को विभाजित करती है।
(viii) सत्य संख्याएँ 4, 6 और 8 और इनका योग 18 से विभाज्य है।
(ix) असत्य संख्याएँ 4 और 9 सहअभाज्य है जो भाज्य संख्याएँ है।
(x) सत्य योग 3 + 5 = 8, 4 से विभाज्य है।
उदाहरण 8.
लुप्त संख्या ज्ञात कीजिए।
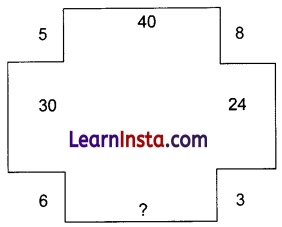
हल:
दी गई पहेली में
5 × 8 = 40
5 × 6 = 30
8 × 3 = 24
? = 6 × 3 = 18
![]()
परीक्षापयोगी प्रश्न
प्रश्न 1.
गुणनखंड और गुणज में क्या अंतर है?
हल:
गुणनखंड और गुणज के बीच प्रमुख अंतर नीचे दिए गए हैं-
| गुणनखंड | गुणज |
| किसी संख्या के गुणनखंड को दी गई संख्या के सटीक भाजक के रूप में परिभाषित किया जाता है। | किसी संख्या के गुणज को उस संख्या के रूप में परिभाषित किया जाता है जो उसे किसी प्राकृतिक संख्या से गुणा करके प्राप्त की जाती है। |
| उदाहरण के लिए 20 के गुणनखंड 1, 2, 3, 4, 5, 10 और 20 हैं। | उदाहरण के लिए 20 के गुणज 20, 40, 60, 80, 100 आदि हैं। |
प्रश्न 2.
निम्नलिखित में से प्रत्येक के प्रथम 5 गुप्त लिखिए।
(a) 23
(b) 40
हल:
(a) 23 के प्रथम पाँच गुणज
23, 46, 69, 92, 115 है।
(b) 40 के प्रथम पाँच गुणज
40, 80, 120, 160, 200 है।
प्रश्न 3.
25 के गुणनखंड और गुणज लिखिए।
हल:
25 के गुणनखंड 1, 5 और 25 हैं।
25 के गुणज 25, 50, 75, 100, 125, 150 इत्यादि हैं।
प्रश्न 4.
क्या 4 के गुणज सम संख्याएँ हैं?
हल:
4 के गुणज 4, 8, 12, 16, 20 हैं।
हाँ, 4 के गुणज सम संख्याएँ हैं। चूँकि 4 एक सम संख्या है, इसलिए 4 के गुणज भी सम संख्याएँ हैं।
प्रश्न 5.
क्या 3 के गुणज हमेशा 6 के गुणज होते हैं?
हल:
3 के गुणज 3, 6, 9, 12, 15, 18, 21, … हैं। अतः 3 के गुणा हमेशा 6 के गुणज नहीं होते हैं। क्योंकि 9, 15, 21, 6 के गुणज नहीं हैं।
प्रश्न 6.
निम्न के सार्व गुणनखंड ज्ञात कीजिए ।
(a) 4, 8 और 12
(b) 5, 15 और 25
हल:
(a) दी गई संख्याएँ हैं – 4, 8 और 12
4 के गुणनखंड 1, 2, 4 हैं। 8 के गुणनखंड 1, 2, 4, 8 हैं। 12 के गुणनखंड 1, 2, 3, 4, 6, 12 हैं।
इसलिए 4, 8 और 12 के सार्व गुणनखंड 1, 2 और 4 हैं।
(b) दी गई संख्याएँ 5, 15 और 25 है।
5 के गुणनखंड 1, 5 हैं।
15 के गुणनखंड 1, 3, 5, 15 हैं।
25 के गुणनखंड 1, 5, 25 है।
इसलिए 5, 15 और 25 के सार्व गुणनखंड 1 और 5 हैं।
![]()
प्रश्न 7.
स्तंभ A को स्तंभ B से सुमेलित करें।
| स्तंभ 1 | स्तंभ 2 |
| (i) 35 | (a) 8 का गुणज |
| (ii) 15 | (b) 7 का गुणज |
| (iii) 16 | (c) 70 का गुणज |
| (iv) 20 | (d) 30 का गुणनखंड |
| (v) 25 | (e) 50 का गुणनखंड |
| (f) 20 का गुणनखंड |
हल:
| स्तंभ 1 | स्तंभ 2 |
| (i) 35 | (b) 7 का गुणज |
| (ii) 15 | (d) 30 का गुणनखंड |
| (iii) 16 | (a) 8 का गुणज |
| (iv) 20 | (f) 20 का गुणनखंड |
| (v) 25 | (e) 50 का गुणनखंड |
प्रश्न 8.
3 और 15 का उभयनिष्ठ गुणनखंड क्या है?
हल:
3 के गुणनखंड 1 और 3 हैं।
15 के गुणनखंड 1, 3, 5 और 15 हैं।
इसलिए 3 और 15 का उभयनिष्ठ गुणनखंड 3 है।
प्रश्न 9.
20 और 6 का उभयनिष्ठ गुणनखंड ज्ञात कीजिए।
हल:
20 के गुणनखंड 1, 2, 4, 5, 10 और 20 हैं। 6 के गुणनखंड 1, 2, 3 और 6 हैं इस प्रकार 6 और 20 का उभयनिष्ठ गुणनखंड 2 है।
प्रश्न 10.
3 और 5 के सार्व गुणज ज्ञात कीजिए।
हल:
3 के गुणज 3, 6, 9, 12, 15, 18, 21, 24, 27, 30….. हैं।
5 के गुणज 5, 10, 15, 20, 25, 30, 35, 40… हैं। इसलिए 3 और 5 के सार्व गुणज 15, 30, 45, 60, इत्यादि हैं।
प्रश्न 11.
क्या 6 एक अभाज्य संख्या या भाज्य संख्या है?
हल:
6 एक भाज्य संख्या है क्योंकि इसे 3 से अधिक संख्याओं
1, 2, 3 और 6 में विभाजित किया जा सकता है।
प्रश्न 12.
1 को अभाज्य संख्या नहीं माना जाता है, क्यों?
हल:
क्योंकि इसके दो अलग-अलग गुणनखंड नहीं हैं। (यानी 1 और संख्या स्वयं समान हैं)
प्रश्न 13.
निम्नलिखित में से कौन सी अभाज्य संख्या है?
(a) 23
(b) 18
(c) 25
(d) 15
हल:
(a) 23 = 1 × 23
अतः 23 एक अभाज्य संख्या है।
(b) चूँकि 18 = 1 × 18 या 6 × 3
अतः 18 एक अभाज्य संख्या नहीं है।
(c) चूँकि 25 = 1 × 25 या 5 × 5
अतः 25 एक अभाज्य संख्या नहीं है।
(d) चूँकि 15 = 1 × 15 या 3 × 5
अतः 15 एक अभाज्य संख्या नहीं है।
अतः विकल्प (a) सही है।
![]()
प्रश्न 14.
संख्याएँ 13 और 31 अभाज्य संख्याएँ हैं। इन दोनों संख्याओं के अंक 1 और 3 समान हैं। 100 तक अभाज्य संख्याओं के ऐसे युग्म ज्ञात कीजिए।
हल:
100 तक अभाज्य संख्याओं के अभीष्ट युग्म 17 और 71, 37 और 73, 79 और 97 हैं।
प्रश्न 15.
रिक्त स्थान भरें।
(i) …………………….. न तो अभाज्य संख्या है और न ही भाज्य संख्या है।
हल:
1
(ii) ………………….. सबसे छोटी अभाज्य संख्या है।
हल:
2
(iii) ………………….. एकमात्र सम अभाज्य संख्या है।
हल:
2
(iv) 1 न तो ……………….. है और न ही ……………….. ।
हल:
भाज्य, अभाज्य
(v) वह संख्या जिसके 2 से अधिक गुणनखंड हों, …………………….. संख्या कहलाती है।
हल:
भाज्य होगी
(vi) ………………. सबसे छोटी भाज्य संख्या है।
हल:
4
(vii) एक अभाज्य संख्या के केवल ……………………………… गुणनखंड होते हैं।
हल:
2
(viii) सबसे छोटी विषम अभाज्य संख्या …………………………… है।
हल:
3
(ix) प्रथम तीन अभाज्य संख्याओं को गुणा करने पर प्राप्त संख्या …………………………
हल:
30
प्रश्न 16.
निम्नलिखित के बीच सभी भाज्य संख्याएँ सूचीबद्ध करें-
(i) 10 और 18
(ii) 61 और 69
(iii) 91 और 96
हल:
(i) 10 और 18 के बीच भाज्य संख्याएँ 12, 14, 15 और 16 हैं।
(ii) 61 और 69 के बीच भाज्य संख्याएँ 62, 63, 64, 65, 66 और 68 हैं।
(iii) 91 और 96 के बीच भाज्य संख्याएँ 92, 93, 94 और 95 हैं।
प्रश्न 17.
सत्य (T) या असत्य (F) लिखिए-
(i) 1, एक अभाज्य संख्या है।
(ii) 1-20 के बीच 8 अभाज्य संख्याएँ हैं।
(iii) 12 एक अभाज्य संख्या है।
(iv) 21 के 4 गुणनखंड हैं- 1, 3, 7 और 21
(v) 4, 6, 7, 8 और 9 भाज्य संख्याएँ हैं
(vi) क्रमागत संख्याएँ हमेशा सहअभाज्य होती हैं, (जिनका HCF 1 होता है)
हल:
(i) असत्य
(ii) सत्य
(iii) असत्य
(iv) सत्य
(v) असत्य (7 अभाज्य संख्या है)
(vi) सत्य
प्रश्न 18.
सभी अभाज्य संख्याएँ चुनें-

हल:
19, 7, 11, 13, 23, 37
प्रश्न 19.
30 से छोटी सभी भाज्य संख्याएँ लिखिए।
हल:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28
प्रश्न 20.
20 से छोटी सभी अभाज्य संख्याएँ लिखिए।
हल:
2, 3, 5, 7, 11, 13, 17, 19
![]()
प्रश्न 21.
1 से 40 के बीच की सभी भाज्य संख्याएँ लिखिए।
हल:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40..
प्रश्न 22.
जाँच कीजिए कि निम्नलिखित भाज्य संख्याएँ हैं या नहीं
(i) 98
(ii) 47
(iii) 35
(iv) 69
(v) 108
(vi) 19
(vii) 21
(viii) 103
हल:
(i) 98 के गुणनखंड 1, 2, 7, 14, 49 और 98 हैं। इसलिए 98 एक भाज्य संख्या है।
(ii) 47 के गुणनखंड 1 और 47 हैं।
इसलिए 47 एक भाज्य संख्या नहीं है। यह एक अभाज्य संख्या है।
(iii) 35 के गुणनखंड 1, 5, 7, 35 हैं।
अतः 35 एक भाज्य संख्या है।
(iv) 69 के गुणनखंड 1, 3, 23, 69 हैं।
अतः 69 एक भाज्य संख्या है।
(v) 108 के गुणनखंड 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54 और 108 हैं।
इसलिए 108 एक भाज्य संख्या है।
(vi) 19 के गुणनखंड 1 और 19 हैं इसलिए 19 एक भाज्य संख्या नहीं है।
(vii) 21 के गुणनखंड 1, 3, 7, 21 हैं।
अतः 21 एक भाज्य संख्या है।
(viii) 103 के गुणनखंड 1 और 103 हैं
इसलिए 103 एक भाज्य संख्या नहीं है।
प्रश्न 23.
निम्नलिखित में से कौन-सा संख्या युग्म सह-अभाज्य है-
(i) 15 और 38
(ii) 25 और 26
(iii) 12 और 18
हल:
(i) यहाँ 15 के गुणनखंड 1, 3, 5, 15 हैं और 38 के गुणनखंड 1, 2, 19, 38 हैं
15 और 38 का HCF = 15 और 38 के सार्व गुणनखंड = 1
चूँकि 15 और 38 का HCF 1 है। अतः 15 और 38 सह – अभाज्य संख्याएँ हैं।
(ii) यहाँ 25 के गुणनखंड 1, 5, 25 हैं और 26 के गुणनखंड 1, 2, 13, 26 हैं। 25 और 26 का HCF = 25 और 26 के सार्व गुणनखंड = 1 चूँकि 25 और 26 का HCF 1 है।
अतः 25 और 26 सह – अभाज्य संख्याएँ हैं।
(iii) यहाँ 12 के गुणनखंड हैं- 1, 2, 3, 4, 6, 12 और 18 के गुणनखंड हैं- 1, 2, 3, 6, 9, 18, 12 और 18 का HCF = 12 और 18 के सार्व गुणनखंड = 1, 2 और 3
चूँकि 1, 2 और 3, 12 और 18 के गुणनखंड हैं।
इसलिए ये सह-अभाज्य नहीं हैं।
प्रश्न 24.
सह – अभाज्य संख्याओं के पाँच युग्म ज्ञात कीजिए।
हल:
(3, 5); (4, 9); (7, 10); (20, 29); (31, 65).
प्रश्न 25.
क्या 40 और 78 सह – अभाज्य हैं?
हल:
चूँकि दो सम संख्याओं के हमेशा दो सार्व गुणनखंड 1 और 2 होते हैं, इसलिए वे कभी भी सह अभाज्य संख्याएँ नहीं हो सकतीं। इस प्रकार 40 और 78 सह – अभाज्य संख्याएँ नहीं हैं।
प्रश्न 26.
सत्य (T) या असत्य (F) बताएँ-
(i) अभाज्य संख्याओं का योग अभाज्य नहीं हो सकता।
(ii) अभाज्य संख्याओं का गुणनफल अभाज्य नहीं हो सकता।
(iii) सम संख्या भाज्य होती है।
(iv) दो क्रमागत संख्याएँ दोनों अभाज्य नहीं हो सकतीं।
(v) विषम संख्याएँ भाज्य नहीं हो सकतीं।
(vi) विषम संख्याओं को अभाज्य संख्याओं के योग के रूप में नहीं लिखा जा सकता।
(vii) एक संख्या और उसका परवर्ती सदैव सह – अभाज्य संख्याएँ होती हैं।
हल:
(i) असत्य। 2 + 3 = 5 एक अभाज्य संख्या है।
(ii) सत्य। अभाज्य संख्याओं का गुणनफल एक भाज्य संख्या होती है।
(iii) असत्य। सम संख्या 2 भाज्य नहीं है।
(iv) असत्य। संख्याएँ 2 और 3 क्रमागत और अभाज्य संख्याएँ हैं।
(v) असत्य। 9 एक विषम संख्या है तथा इसके खंड 1, 3 तथा 9 हैं।
(vi) असत्य। 9 एक विषम संख्या है तथा अभाज्य संख्या 7 + 2 = 9 का योग है।
(vii) सत्य। एक संख्या और उसके परवर्ती का केवल एक ही उभयनिष्ठ गुणनखंड होता है।
![]()
प्रश्न 27.
126000 का अभाज्य गुणनखंडन ज्ञात कीजिए।
हल:
यहाँ,

अतः 126000 का अभाज्य गुणनखंडन 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5 × 7. है ।
प्रश्न 28.
सत्य / असत्य बताइए – 5 × 33, 165 का अभाज्य गुणनखंडन है।
हल:
असत्य।
प्रश्न 29.
256 और 156 के सार्व अभाज्य गुणनखंडों की सूची बनाइए।
हल:
256 का अभाज्य गुणनखंडन = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
156 का अभाज्य गुणनखंडन = 2 × 2 × 3 × 13
256 और 156 के सार्व अभाज्य गुणनखंड 2 है।
प्रश्न 30.
152 और 76 के सार्व गुणनखंडों की सूची बनाइए ।
हलः
152 का अभाज्य गुणनखंडन = 2 × 2 × 2 × 19
76 का अभाज्य गुणनखंडन = 2 × 2 × 19
152 और 76 के सार्व अभाज्य गुणनखंड 2 और 19 हैं।
प्रश्न 31.
सही विकल्प पर (✓) का निशान लगाएँ।
(i) 54 का अभाज्य गुणनखंडन है।
(a) 2 × 27
(b) 2 × 3 × 9
(c) 54 × 1
(d) 2 × 3 × 3 × 3
हल:
(d) 2 × 3 × 3 × 3
(ii) 2 × 3 × 7 इसका अभाज्य गुणनखंडन है
(a) 21
(b) 1237
(c) 237
(d) 42
हल:
(d) 42
प्रश्न 32.
निम्नलिखित संख्याओं के अभाज्य गुणनखंडन ज्ञात कीजिए-
(i) 18
(ii) 39
(iii) 385
(iv) 45
(v) 52
(vi) 64
(vii) 390
(viii) 2520
(ix) 1210
(x) 1260
(xi) 1024
(xii) 2520
हल:
(i) 18 = 1 × 2 × 3 × 3
(ii) 39 = 1 × 3 × 13
(iii) 385 = 1 × 5 × 7 × 11
(iv) 45 = 1 × 3 × 3 × 5
(v) 52 = 1 × 2 × 2 × 13
(vi) 64 = 2 × 2 × 2 × 2 × 2 × 2
(vii) 390 = 2 × 3 × 5 × 13
(viii) 2520 = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 7
(ix) 1210 = 2 × 5 × 11 × 11
(x) 1260 = 1 × 2 × 2 × 3 × 3 × 5 × 7
(xi) 1024 = 1 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
(xii) 2520 = 1 × 2 × 2 × 2 × 3 × 3 × 5 × 7 × 2
![]()
प्रश्न 33.
9 का विभाज्यता नियम लिखिए।
हल:
दी गई संख्या के अंकों का योग 9 से विभाज्य होना चाहिए। उदाहरण के लिए 2979, 9 से विभाज्य है।
(अर्थात्) 2 + 9 + 7 + 9 = 27, जो कि 9 से विभाज्य है।
प्रश्न 34.
निम्नलिखित में से कौन-सी संख्याएँ 2, 5 और 10 से विभाज्य हैं?
(i) 149
(ii) 19400
(iii) 720345
(iv) 125370
(v) 3000000
हल:
(ii) 19400,
(iv) 125370,
(v) 3000000
प्रश्न 35.
जाँच करें कि संख्याएँ 4 से विभाज्य हैं या नहीं।
(i) 23408
(ii) 100246
हल:
(i) दी गई संख्या 23408 है।
यहाँ 23408 के अंतिम 2 अंक 08 हैं।
यह 4 से विभाज्य है। (∵ \(\frac{1}{2}\) = 2)
अतः 23408, 4 से विभाज्य है।
(ii) दी गई संख्या 100246 है।
अब 100246 के अंतिम 2 अंक 46 हैं जो 4 से विभाज्य नहीं है। अतः 100246, 4 से विभाज्य नहीं है।
प्रश्न 36.
निम्नलिखित प्रत्येक संख्या में वास्तविक विभाजन न करते हुए, ज्ञात करें कि पहली संख्या दूसरी संख्या से विभाज्य है या नहीं।
(i) 3409122; 6
(ii) 11309634; 8
(iv) 3501804; 4
हल:
(i) आइए ज्ञात करें कि क्या 3409122, 6 से विभाज्य है।
6 का विभाज्यता नियम 2 और 3 के नियमों को जोड़ता है।
यहाँ 3409122 सम संख्या है क्योंकि इसका अंतिम अंक 2 है। अतः दी गई संख्या 2 से विभाज्य है। इसके अंकों का योग है।
3 + 4 + 0 + 9 + 1 + 2 + 2 = 21
जो 3 से विभाज्य है।
इस प्रकार दी गई संख्या 3 से भी विभाज्य है।
अतः 3409122, 6 से भी विभाज्य है।
(ii) दी गई संख्या 11309634 है यहाँ 11309634 के अंतिम 3 अंक 634 है।
अब
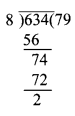
जो 8 से विभाज्य नहीं है।
अतः 11309634, 8 से विभाज्य नहीं है।
(iii) दी गई संख्या 3501804 है और 3501804 के अंतिम 2 अंक 04 हैं।
यह 4 से विभाज्य है।
अतः 3501804 4 से विभाज्य है।
प्रश्न 37.
संख्या को विभाज्य बनाने के लिए सबसे छोटा अंक भरें-
(i) 5 से : 7164_, 32197_
(ii) 7 से : 1_43, 47_05, _316
(iii) 6 से _428, 9_52, 721_
(iv) 4 से : 2462_, 91_ _, 670_
(v) 8 से : 1232__, 59_16, 4642_
हल:
(i) 0,0
(ii) 1, 2, 2
(iii) 1, 2, 2
(iv) 0, 00, 0
(1) 0, 0, 4
प्रश्न 38.
19506 के निकटतम दो संख्याओं में से कौन-सी 97 से विभाज्य है?
हल:
19503, 19512
प्रश्न 39.
सही उत्तर चुनें-
(i) इकाई अंक 0 या 5 वाली संख्या किससे विभाज्य है?
(a) 2
(b) 3
(c) 4
(d) 5
हल:
(d) 5
(ii) इकाई अंक 0, 2, 4, 6 या 8 वाली संख्या किससे विभाज्य है?
(a) 2
(b) 3
(c) 4
(d) 5
हल:
(a) 2
(iii) इकाई अंक 0 वाली संख्या किससे विभाज्य है?
(a) 5
(b) 10
(c) 15
(d) 2
हल:
(b) 10
(iv) 1170 किससे विभाज्य नहीं है?
(a) 10
(b) 9
(c) 5
(d) 4
हल:
(d) 4
![]()
प्रश्न 40.
सत्य या असत्य बताइए-
(i) यदि दो संख्याएँ किसी संख्या से विभाज्य हैं, तो उनका योग, अंतर और गुणनफल भी उस संख्या से विभाज्य होंगे।
(ii) 11 से विभाज्य सबसे बड़ी 4- अंकीय संख्या 9999 है।
(iii) जो संख्याएँ 2 से विभाज्य नहीं होती उन्हें सम संख्याएँ कहते हैं।
हल:
(i) सत्य
(ii) सत्य
(iii) असत्य
प्रश्न 41.
स्तंभों का मिलान करें-
| स्तंभ A | स्तंभ B |
| (i) 2023 | (a) 3 से विभाज्य |
| (ii) 24804 | (b) 11 से विभाज्य |
| (iii) 12892 | (c) 8 से विभाज्य |
| (iv) 6016 | (d) 7 से विभाज्य |
हल:
(i) → (d)
(ii) → (a)
(iii) → (b)
(iv) → (c)
| स्तंभ A | स्तंभ B |
| (i) 2023 | (d) 7 से विभाज्य |
| (ii) 24804 | (a) 3 से विभाज्य |
| (iii) 12892 | (b) 11 से विभाज्य |
| (iv) 6016 | (c) 8 से विभाज्य |