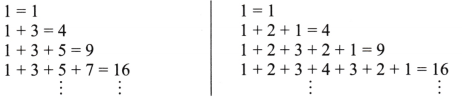Class 6 Maths Chapter 1 Patterns in Mathematics Notes
Class 6 Maths Chapter 1 Notes – Class 6 Patterns in Mathematics Notes
Number Patterns
A list of numbers that follow a certain sequence is known as a number pattern.
For example, patterns of whole numbers 0, 1, 2, 3, 4, 5,…
The study of these number patterns of whole numbers is called number theory.
Number Sequences Number sequences are the most basic and among the most fascinating types of patterns that mathematicians study.
Examples of Number Sequence
- All l’s – 1, 1, 1, 1, 1,…..
- Natural Numbers – 1, 2, 3, 4, 5,…..
- Even Number – 2, 4, 6, 8, 10,…..
- Odd Numbers – 1, 3, 5, 7, 9,…..
- Triangular Numbers – 1, 3, 6, 10, 15, 21, 28,…..
- Squares – 1, 4, 9, 16, 25,…..
- Cubes – 1, 8, 27, 64, 125, 216,…..
- Virahanka Numbers – 1, 2, 3, 5, 8, 13, 21,…..
- Powers of 2 – 1, 2, 4, 8, 16, 32,……
- Powers of 3 – 1, 3, 9, 27, 81, 243,…..
- All the above sequences have a specific pattern or rule that determines the next number.
- In the sequence of even numbers, you add 2 to get the next number (2 + 2 = 4, 4 + 2 = 6, and so on).
Example 1.
Can you identify the pattern in the sequence 1, 4, 7, 10, 13, 16,……?
Solution:
Yes, We have, 1, 4, 7, 10, 13, 16,…..
Here, the difference between the two consecutive numbers is 3.
Example 2.
Write the next two terms in the following sequence, 15, 30, 60, 120,…….
Solution:
We have, 15, 30, 60, 120,…..
Here, the next term is twice of the previous term.
∴ The next two terms are 240 and 480.
Visualizing Number Sequences
Visualizing number sequences is a great way to understand patterns and relationships in numbers. Sequences often form visual patterns that can be represented with shapes. A pictorial representation of some number sequences is given below.
All 1’s The all 1’s sequence is an infinite sequence where each term is 1.
e.g. 1, 1, 1, 1,….

![]()
Natural Numbers:
Natural numbers include all the whole numbers excluding the number 0.
The sequence of natural numbers is counting starting from the number 1 until infinity.
e.g. 1, 2, 3, 4,……….

Odd Numbers:
The sequence of odd numbers is given as 1, 3, 5, 7, ……..(2n – 1).
The sequence follows each other by the difference of 2.

Even Numbers:
Even the number is divisible by 2 and leaves the remainder 0.
To get the sequence of even numbers add 2 in the previous even number.
e.g. 2, (2 + 2), (2 + 2 + 2), (2 + 2 + 2 + 2),
i.e. 2, 4, 6, 8,……..

Triangular Numbers:
Triangular numbers are numbers that make up the sequence 1, 3, 6, 10,…….
The next triangular number in the sequence is the number of dots it would take to make an equilateral triangle with dots on each side.

Squares:
When we multiply a number times itself the resulting product is called a square number.
The square numbers can form a sequence as 1, 4, 9, 16, 25,………

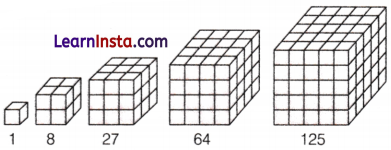
Cubes:
The sequence of numbers that results from cubing each integer in turn.
e.g. 1, 8, 27, 64, 125,……..
![]()
Example 3.
Draw the sequence of all 2’s.
Solution:

Relations Among Number Sequences
Sometimes, different number sequences are surprisingly related to each other.
e.g. What do we get if we add up odd numbers?
1 = 1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
1 + 3 + 5 + 7 + 9 + 11 = 36 and so on.
Here, we get always a square number.
The above pattern happens every time. We can explain it by picture visualization.

By this method, we can easily find the sum of the first 10 and 100 odd numbers is 10 × 10 and 100 × 100, respectively.
Hence, the sum of the first n odd numbers is n2.
Example 4.
Find the sum of the first 50 and add numbers.
Solution:
We know that the sum of the first n odd numbers = n2
∴ The sum of the first 50 odd numbers = (50)2
= 50 × 50
= 2500
Example 5.
What do we get if we add up and down the natural numbers?
Solution:
1 = 1
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
1+ 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36
Here, also we get square numbers.
Patterns in Shapes
Studying patterns in shapes helps to develop important mathematical skills. It teaches you to recognize and create sequences, understand symmetry, and see how shapes can transform.
Shapes can be one, two, or three-dimensional (1D, 2D or 3D) and can be even more dimensional.
Geometry:
The branch of Mathematics that studies patterns in shapes is called geometry.
Shape Sequences:
The shapes which are repeated over and over following the same order are called shape sequences.
Number sequences can be related to each other in many ways.
e.g. If we add consecutive odd numbers, then we get square numbers.
![]()
Example 6.
Can you identify the next shape sequence?
![]()
Solution:
The next shape will be a circle ![]() , as the sequence is an alternating triangle and circle.
, as the sequence is an alternating triangle and circle.
Relations to Number Sequences
Shape sequences and Number sequences are related to each other in many ways.
Regular Polygons:
A polygon has all its sides equal and so all angles are equal.
In the shape sequence of regular polygons, the number of sides is given by 3, 4, 5, 6, 7, 8,…..
Polygons are named according to their number of sides.
| Number of Sides | Polygon |
| 3 | Triangle |
| 4 | Quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| 9 | Nonagon |
| 10 | Decagon |
→ there are indeed patterns everywhere we look—in nature, in our houses and schools, and the movements of the earth, moon, and stars in our solar system. Also, they are present in everything we do and observe, including buying, cooking, playing games, comprehending weather patterns, and utilizing technology.
→ A significant portion of mathematics is looking for patterns and finding the reasons behind them.
→ Mathematics is not just for what patterns exist but also for the explanations for why those patterns exist. Among the most basic patterns that occur in mathematics are patterns of numbers, particularly patterns of whole numbers: 0, 1, 2, 3, 4, 5,…
→ Some number patterns are: Counting numbers, sequences of even and odd numbers, triangular numbers, square numbers, etc. We can also visualize these number patterns.
→ One of the important patterns that occur in Mathematics is patterns of shapes. These shapes may be in one, two, or three dimensions (1D, 2D, or 3D) — or even more dimensions.
→ Sequences of shapes frequently have unexpected relationships with sequences of numbers.
![]()
→ Number sequences are the most basic and among the most fascinating types of patterns. For example,
- 1, 3, 5, 7, 9, … (Odd numbers)
- 2, 4, 6, 8, 10, … (Even numbers)
- 1, 4, 9, 16, 25, … (Square numbers)
- 1, 3, 6, 10, 15, 21, 28, … (Triangular numbers), etc.
→ Many number sequences can be visualized using pictures. A few of them are shown below:

→ Power is an expression that shows repeated multiplication of the same number or factor.
→ Powers of 2 are numbers that are obtained when 2 is raised to a power of any whole number.
→ For example, 2 to the power of 1 means 2, 2 to the power of 2 means 2 × 2 = 4, 2 to the power of 3 means 2 × 2 × 2 = 8, etc.
→ Powers of 3 are numbers that are obtained when 3 is raised to a power of any whole number. For example, 3 to the power of 1 means 3, 3 to the power of 2 means 3 × 3 = 9, 3 to the power of 3 means 3 × 3 × 3 = 27, 3 to the power of 4 means 3 × 3 × 3 × 3 = 81, etc.
![]()
→ Any counting (natural) number raised to the 0 power means always 1.
→ For example, 2 to the power of 0 means 1, 5 to the power of 0 means 1, etc. (Note: You will study about the powers in the next classes).
→ Number sequences can be related to each other in surprising ways. For example,