Here we are providing Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.
Extra Questions for Class 10 Maths Pair of Linear Equations in Two Variables with Answers Solutions
Extra Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables with Solutions Answers
Pair of Linear Equations in Two Variables Class 10 Extra Questions Very Short Answer Type
Question 1.
If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find value of k.
Solution:
Since the given lines are parallel
![]()
Question 2.
Find the value of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 will have infinitely many solutions.
Solution:
The given system of equations will have infinitely many solutions if \(\frac{c}{6}=\frac{-1}{-2}=\frac{2}{3}\) which is not possible
∴ For no value of c, the given system of equations have infinitely many solutions.
Question 3.
Do the equations 4x + 3y – 1 = 5 and 12x + 9y = 15 represent a pair of coincident lines?
Solution:
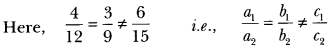
Given equations do not represent a pair of coincident lines.
Question 4.
Find the co-ordinate where the line x – y = 8 will intersect y-axis.
Solution:
The given line will intersect y-axis when x = 0.
∴0 – y = 8 ⇒ y = -8
Required coordinate is (0, -8).
Question 5.
Write the number of solutions of the following pair of linear equations:
x + 2y – 8 = 0, 2x + 4y = 16
Solution:
![]()
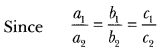
∴The given pair of linear equations has infinitely many solutions.
Pair of Linear Equations in Two Variables Class 10 Extra Questions Short Answer Type 1
Question 1.
Is the following pair of linear equations consistent? Justify your answer.
2ax + by = a, 4ax + 2by – 2a = 0; a, b≠ 0
Solution:
Yes,
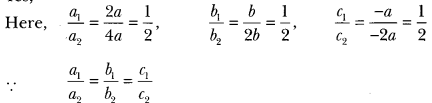
∴ The given system of equations is consistent.
Question 2.
For all real values of c, the pair of equations
x – 2y = 8, 5x + 10y = c
have a unique solution. Justify whether it is true or false.
Solution:
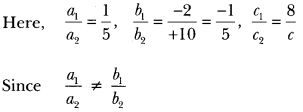
So, for all real values of c, the given pair of equations have a unique solution.
∴ The given statement is true.
Question 3.
Does the following pair of equations represent a pair of coincident lines? Justify your answer.
\(\frac{x}{2}\) + y + \(\frac{2}{5}\) = 0, 4x+ 8y + \(\frac{5}{16}\) = 0.
Solution:
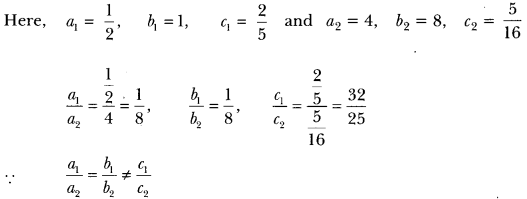
∴ The given system does not represent a pair of coincident lines.
Question 4.
If x = a, y = b is the solution of the pair of equation x – y = 2 and x + y = 4, then find the value of a and b.
Solution:
x – y = 2 … (i)
x + y = 4 … (ii)
On adding (i) and (ii), we get 2x = 6 or x = 3
From (i), 3 – y ⇒ 2 = y = 1
a = 3, b = 1.
On comparing the ratios \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) , and, \(\frac{c_{1}}{c_{2}}\) find out whether the following pair of linear equations consistent or inconsistent. is consistent or inconsistent. (Q. 5 to 6)
Question 5.
\(\frac{3}{2}\) x + \(\frac{5}{3}\) y = 7
9x – 10y = 14
Solution:
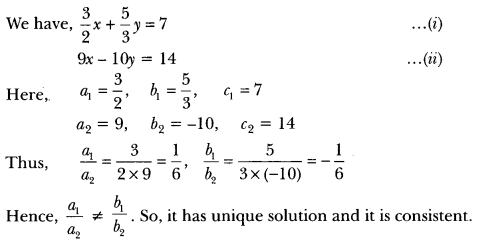
Question 6.
\(\frac{4}{3}\) x + 2y = 8;
2x + 3y = 12
Solution:
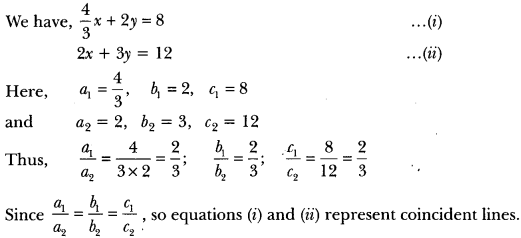
Hence, the pair of linear equations is consistent with infinitely many solutions.
On comparing the ratios \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\), and \(\frac{c_{1}}{c_{2}}\), find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident: (Q. 7 to 9).
Question 7.
5x – 4y + 8 = 0
7x + 6y – 9 = 0
Solution:
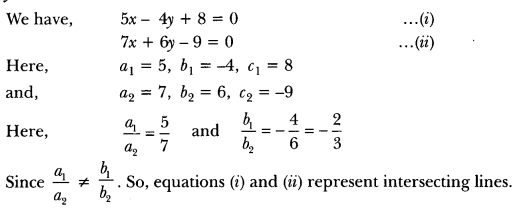
Question 8.
9x + 3y + 12 = 0
18x + 6y + 24 = 0
Solution:
We have,
9x + 3y + 12 = 0
18x + 6y + 24 = 0
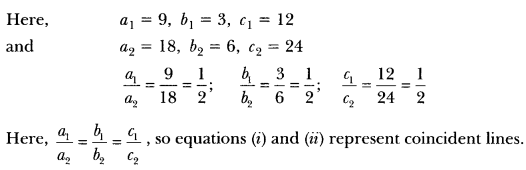
Question 9.
6x – 3y + 10 = 0 .
2x – y + 9 = 0
Solution:

Pair of Linear Equations in Two Variables Class 10 Extra Questions Short Answer Type 2
Question 1.
Solve: ax + by = a – b and bx – ay = a + b
Solution:
The given system of equations may be written as
ax + by – (a – b) = 0
bx – ay – (a + b) = 0
By cross-multiplication, we have
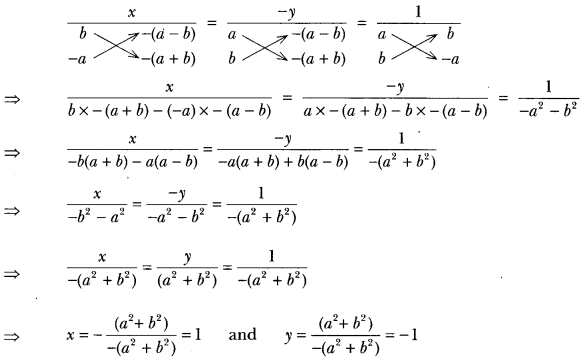
Hence, the solution of the given system of equations is x = 1, y = -1
Question 2.
Solve the following linear equations:
152x – 378y = -74 and -378x + 152y = -604
Solution:
We have, 152x – 378y = -74 …(i)
-378x + 152y = -604 ……(ii)

Putting the value of x in (iii), we get
2 + y = 3 ⇒ y = 1
Hence, the solution of given system of equations is x = 2, y = 1.
Question 3.
Solve for x and y
![]()
Solution:
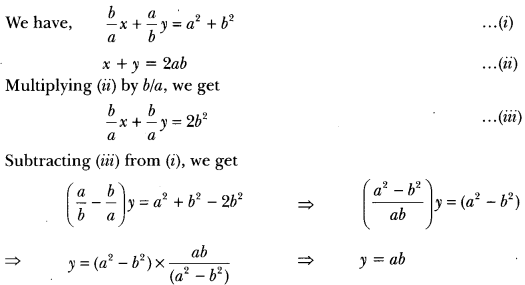
Putting the value of y in (ii), we get
x + ab = 2ab ⇒ x = 2ab – ab ⇒ x = ab
∴ x = ab, y = ab
Question 4.
(i) For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7
(a – b)x + (a + b)y = 3a + b – 2
(ii) for which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
Solution:
(i) We have, 2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2 … (ii)
Here, a1 = 2, b1 = 3, c1 = 7 and
a2 = a – b, b2 = a + b, c2 = 3a + b – 2
For infinite number of solutions, we have
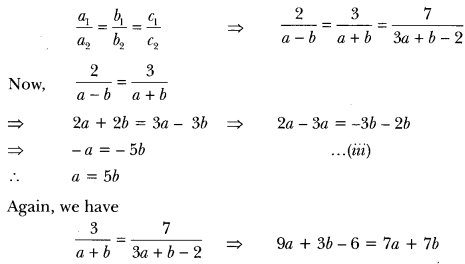
⇒ 9a – 7a + 3b – 75 -6 = 0 ⇒ 2a – 45 – 6 = 0 => 2a – 4b = 6
⇒ a – 2b = 3 …(iv)
Putting a = 5b in equation (iv), we get
56 – 2b = 3 or 3b = 3 i.e., b = \(\frac{3}{3}\) =1
Putting the value of b in equation (ii), we get a = 5(1) = 5
Hence, the given system of equations will have an infinite number of solutions for a = 5 and b = 1.
(ii) We have, 3x + y = 1, 3x + y − 1 = 0 …(i)
(2k – 1) x + (k – 1) y = 2k + 1
⇒ (2k – 1) x + (k – 1) y – (2k + 1) = 0 ……(ii)
Here, a1 = 3, b1 = 1, C1 = -1
a2 = 2k – 1, b2 = k – 1, C2 = -(2k + 1)
For no solution, we must have
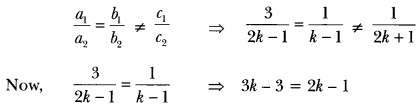
⇒ 3k – 2k = 3 – 1 ⇒ k = 2
Hence, the given system of equations will have no solutions for k = 2.
Question 5.
Find whether the following pair of linear equations has a unique solution. If yes, find the
7x – 4y = 49 and 5x – y = 57
Solution:
We have, 7x – 4y = 49 ……..(i)
and 5x – 6y = 57 ……..(ii)
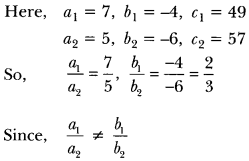
So, system has a unique solution.
Multiply equation (i) by 5 and equation (ii) by 7 and subtract
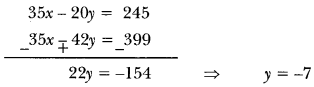
Put y = -7 in equation (ii)
5x – 6(-7)57 ⇒ 5x = 57 – 42 ⇒ x = 3
hence, x = 3 and y = -7.
Question 6.
Solve for x and y.
![]()
Solution:
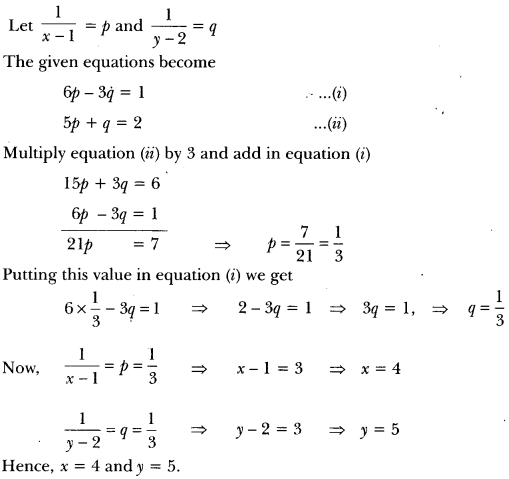
Question 7.
Solve the following pair of equations for x and y.
![]()
Solution:

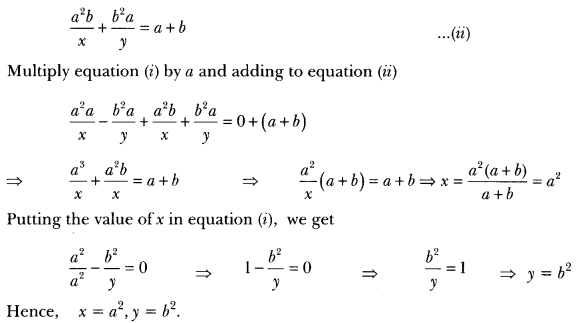
Question 8.
In ∆ABC, LA = x, ∠B = 3x, and ∠C = y if 3y – 5x = 30°, show that triangle is right angled.
Solution:
∠A + 2B + ∠C = 180°
(Sum of interior angles of A ABC) x + 3x + y = 180°
4x + y = 180° …(i)
3y – 5x = 30° (Given) …(ii) Multiply equation (i) by 3 and subtracting from eq. (ii), we get
-17x = – 510 = x = 910 = 30°
17 then _A = x = 30° and 2B = 3x = 3 X 30o = 90°
∠C = y = 180° – (∠A + ∠B) = 180° – 120° = 60°
∠A = 30°, ∠B = 90°, ∠C = 60° Hence ∆ABC is right triangle right angled at B.
Question 9.
In Fig. 3.1, ABCDE is a pentagon with BE|CD and BC||DE. BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm. Find the value of x and y.
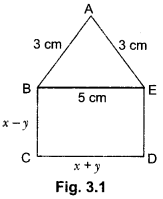
Solution:
Since BC||DE and BE||CD with BC||CD.
BCDE is a rectangle.
Opposite sides are equal BE = CD
∴ x + y = 5 …… (i)
DE = BC = x – y
Since perimeter of ABCDE is 21 cm.
AB + BC + CD + DE + EA = 21
3 + x – y + x + y + x – y + 3 = 21 ⇒ 6 + 3x – y = 21
3x – y = 15 ….. (iii)
Adding (i) and (ii), we get
4x = 20 ⇒ x = 5
On putting the value of x in (i), we get y = 0
Hence, x = 5 and y = 0.
Question 10.
Five years ago, A was thrice as old as B and ten years later, A shall be twice as old as B. What are the present ages of A and B?
Solution:
Let the present ages of B and A be x years and y years respectively. Then
B’s age 5 years ago = (x – 5) years
and A’s age 5 years ago = (- 5) years
(-5) = 3 (x – 5) = 3x – y = 10 …….(i)
B’s age 10 years hence = (x + 10) years
A’s age 10 years hence = (y + 10) years
y + 10 = 2 (x + 10) = 2x – y = -10 …….. (ii)
On subtracting (ii) from (i) we get x = 20
Putting x = 20 in (i) we get
(3 × 20) – y = 10 ⇒ y = 50
∴ x = 20 and y = 50
Hence, B’s present age = 20 years and A’s present age = 50 years.
Question 11.
A fraction becomes when \(\frac{1}{3}\) is subtracted from the numerator and it becomes \(\frac{1}{4}\) when 8 is added to its denominator. Find the fraction.
Solution:
Let the numerator be x and denominator be y.
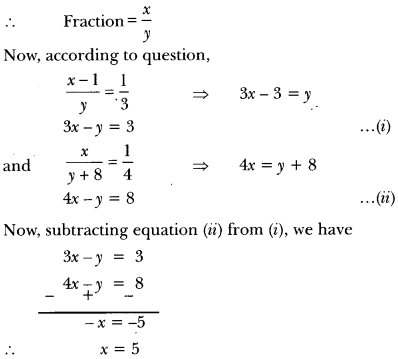
Putting the value of x in equation (i), we have
3 × 5 – y = 3 ⇒ 5 – y = 3 ⇒ 15 – 3 = y
∴ y = 12
Hence, the required fraction is \(\frac{5}{12}\)
Question 12.
Solve the following pairs of equations by reducing them to a pair of linear equations:

Solution:
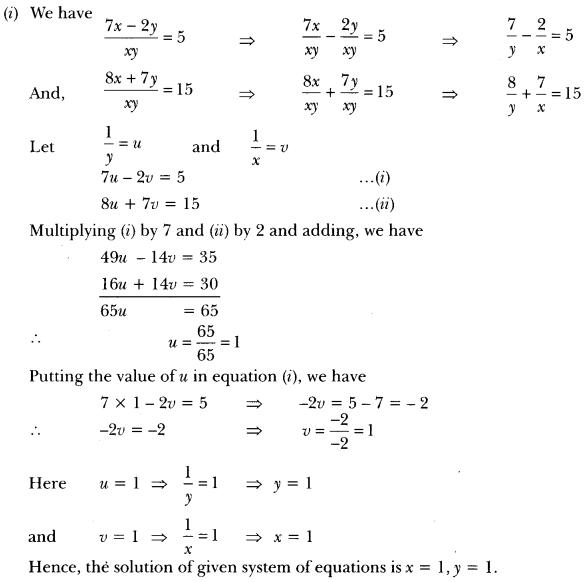
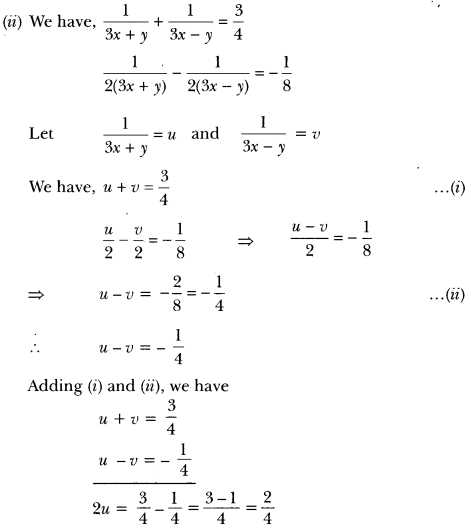
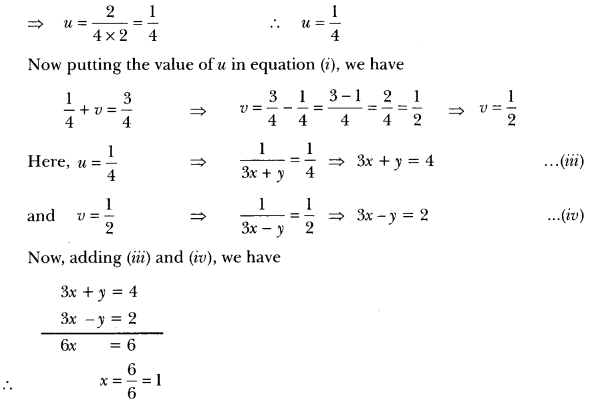
Putting the value of x in equation (iii), we have
3 x 1 + y = 4
⇒ y = 4 – 3 = 1
Hence, the solution of given system of equations is x = 1, y = 1.
Pair of Linear Equations in Two Variables Class 10 Extra Questions Long Answers
Question 1.
Form the pair of linear equations in this problem, and find its solution graphically: 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Solution:
Let x be the number of girls and y be the number of boys.
According to question, we have
x = y + 4
⇒ x – y = 4 ……(i)
Again, total number of students = 10
Therefore, x + y = 10 …(ii)
Hence, we have following system of equations
x – y = 4
and x + y = 10
From equation (i), we have the following table:
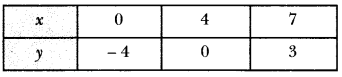
From equation (ii), we have the following table:

Plotting this, we have
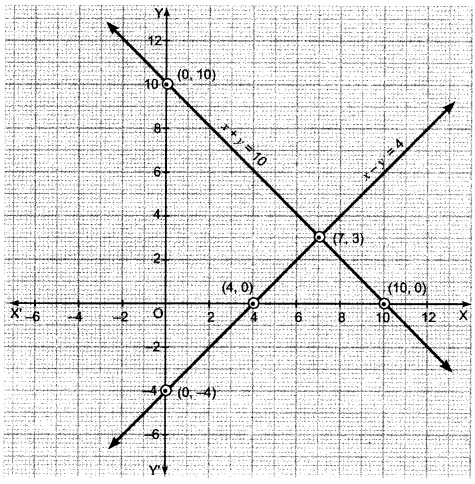
Here, the two lines intersect at point (7,3) i.e., x = 7, y = 3.
So, the number of girls = 7
and number of boys = 3.
Question 2.
Show graphically the given system of equations
2x + 4y = 10 and 3x + 6y = 12 has no solution.
Solution:
We have, 2x + 4y = 10
⇒ 4y = 10 – 2x ⇒ y = \(\frac{5-x}{2}\)
Thus, we have the following table:

Plot the points A (1, 2), B (3, 1) and C (5,0) on the graph paper. Join A, B and C and extend it on both sides to obtain the graph of the equation 2x + 4y = 10.
We have, 3x + 6y = 12
⇒ 6y = 12 – 3x ⇒ y = \(\frac{4-x}{2}\)
Thus, we have the following table :

Plot the points D (2, 1), E (0, 2) and F (4,0) on the same graph paper. Join D, E and F and extend it on both sides to obtain the graph of the equation 3x + 6y = 12.
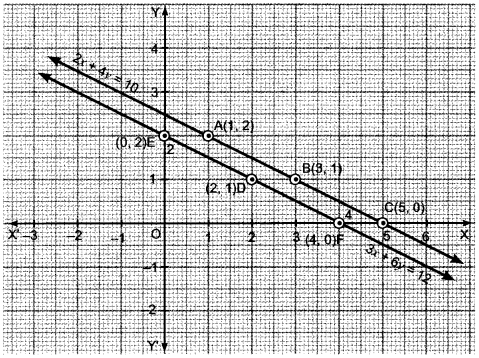
We find that the lines represented by equations 2x + 4y = 10 and 3x + y = 12 are parallel. So, the two lines have no common point. Hence, the given system.of equations has no solution.
Question 3.
Solve the following pairs of linear equations by the elimination method and the substitution method:
(i) 3x – 5y – 4 = 0 and 9x = 2y + 7
(ii) \(\frac{x}{2}+\frac{2 y}{3}\) = -1 and x – \(\frac{y}{3}\) = 3
Solution:
(i) We have, 3x – 5y – 4 = 0
⇒ 3x – 5y = 4 …….(i)
Again, 9x = 2y + 7
9x – 2y = 7 …(ii)
By Elimination Method:
Multiplying equation (i) by 3, we get
9x – 15y = 12 … (iii)
Subtracting (ii) from (iii), we get
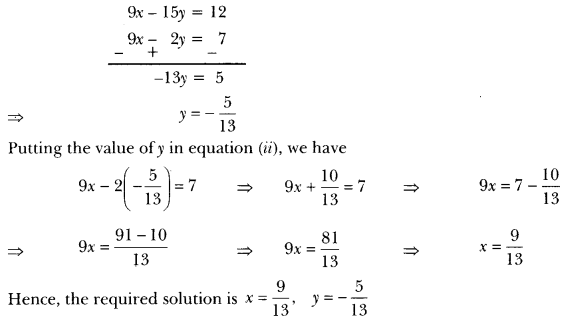
By Substitution Method:
Expressing x in terms of y from equation (i), we have
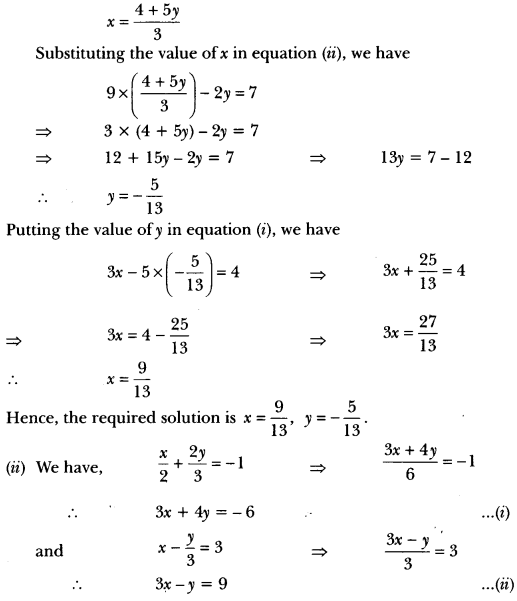
By Elimination Method:
Subtracting (ii) from (i), we have
5y = – 15 or y = – \(\frac{5}{5}\) = -3
Putting the value of y in equation (i), we have
3x + 4 × (-3) = -6 ⇒ 3x = – 6 + 12
∴ 3x – 12 = -6 ⇒ 3x = 6
∴ x = \(\frac{6}{3}\) = 2
Hence, solution is x = 2, y = -3.
By Substitution Method:
Expressing x in terms of y from equation (i), we have
3 × \(\left(\frac{-6-4 y}{3}\right)\) – y = 9 ⇒ -6 – 4y – y = 9 ⇒ -6 – 5y = 9
Substituting the value of x in equation (ii), we have
∴ -5y = 9 + 6 = 15
y = – \(\frac{15}{5}\) = – 3
Putting the value of y in equation (i), we have
3x + 4 × (-3) = -6 ⇒ 3x – 12 = -6
∴ 3x = 12 – 6 = 6
∴ x = \(\frac{6}{3}\) = 2
Hence, the required solution is x = 2, y = – 3.
Question 4.
Draw the graph of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Solution:
We have,’ x – y + 1 = 0 and 3x + 2y – 12 = 0
Thus, x – y = -1 => x = y – 1 …(i)
3x + 2y = 12 => x = \(\frac{12-2 y}{3}\) … (ii)
From equation (i), we have

From equation (ii), we have
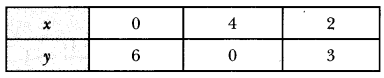
Plotting this, we have
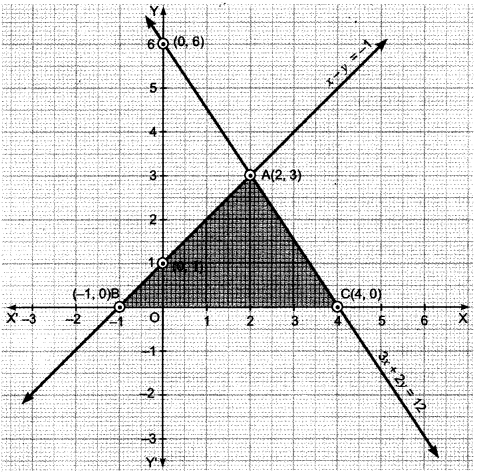
ABC is the required (shaded) region and point of intersection is (2, 3).
∴ The vertices of the triangle are (-1, 0), (4, 0), (2, 3).
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method (Q. 5 to 8):
Question 5.
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days, she has to pay 31000 as hostel charges whereas a student B, who takes food for 26 days, pays 1180 as hostel charges. Find the fixed charges and the cost of food per day.
Solution:
Let the fixed charge be *x and the cost of food per day be by.
Therefore, according to question,
x + 20y = 1000 …(i)
x + 26y = 1180 …(ii)
Now, subtracting equation (ii) from (i), we have
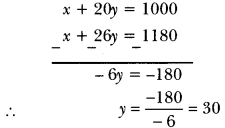
Putting the value of y in equation (i), we have
x + 20 x 30 = 1000 ⇒ x + 600 = 1000 ⇒ x = 1000 – 600 = 400
Hence, fixed charge is ₹400 and cost of food per day is ₹30.
Question 6.
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deduced for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solution:
Let x be the number of questions of right answer and y be the number of questions of wrong answer.
According to question,
3x – y = 40 … (i)
and 4x – 2y = 50
or 2x – y = 25 …(ii)
Subtracting (ii) from (i), we have
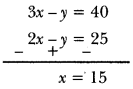
Putting the value of x in equation (i), we have
3 x 15 – y = 40 ⇒45 – y = 40
∴ y = 45 – 40 = 5
Hence, total number of questions is x + yi.e., 5 + 15 = 20.
Question 7.
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
Solution:
Let the speed of two cars be x km/h and y km/h respectively.
Case I: When two cars move in the same direction, they will meet each other at P after 5 hours.
![]()
The distance covered by car from A = 5x (Distance = Speed × Time)
and distance covered by the car from B = 5y
∴ 5x – 5y = AB = 100 ⇒ x – y = \(\frac{100}{5}\)
∴ x – y = 20 ….(i)
Case II: When two cars move in opposite direction, they will meet each other at Q after one hour.
![]()
The distance covered by the car from A = x
The distance covered by the car from B = y
∴ x + y = AB = 100 ⇒ x + y = 100 …..(ii)
Now, adding equations (i) and (ii), we have
2x = 120 ⇒ x = \(\frac{120}{2}\) = 60
Putting the value of x in equation (i), we get
60 – y = 20 ⇒ – y = -40
∴ y = 40
Hence, the speeds of two cars are 60 km/h and 40 km/h respectively.
Question 8.
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solution:
Let the length and breadth of a rectangle be x and y respectively.
Then area of the rectangle = xy
According to question, we have
(x – 5) 6 + 3) = xy – 9 ⇒ xy + 3x – 5y – 15 = xy – 9
⇒ 3x – 5y = 15 – 9 = 6 ⇒ 3x – 5y = 6 …(i)
Again, we have
(x + 3) 6 + 2) = xy + 67 ⇒ xy + 2x + 3y + 6 = xy + 67
⇒ 2x + 3y = 67 – 6 = 61 ⇒ 2x + 3y = 61…. (ii)
Now, from equation (i), we express the value of x in terms of y as
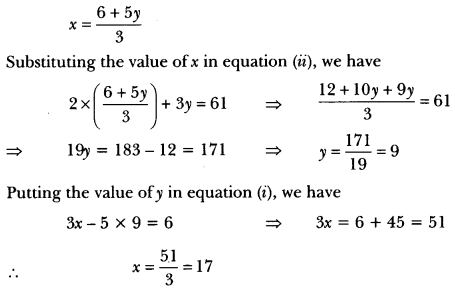
Putting the value of y in equation (i), we have
3x – 5 x 9 = 6 ⇒ 3x = 6 + 45 = 51
∴ x = \(\frac{51}{3}\) = 17
Hence, the length of rectangle = 17 units and breadth of rectangle = 9 units.
Question 9.
Formulate the following problems as a pair of equations, and hence find their solutions:
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) Roobi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by bus and the remaining by train. If she travels 100 km by bus and the remaining by train, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
(i) Let her speed of rowing in still water be x km/h and the speed of the current be y km/h.
Case I: When Ritu rows downstream
Her speed (downstream) = (x + y) km/h

Putting the value of x in equation (i), we have
6 + y = 10 ⇒ y = 10 – 6 = 4
Hence, speed of Ritu in still water = 6 km/h.
and speed of current = 4 km/h.
(ii) Let the speed of the bus be x km/h and speed of the train be y km/h.
According to question, we have

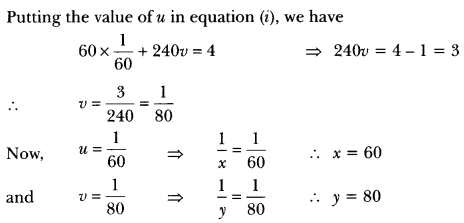
Question 10.
The sum of a two digit number and the number formed by interchanging its digits is 110. If 10 is subtracted from the first number, the new number is 4 more than 5 times the sum of the digits in the first number. Find the first number.
Solution:
Let the digits at unit and tens places be x and y respectively.
Then, number = 10y + x …(i)
Number formed by interchanging the digits = 10x + y
According to the given condition, we have
(10y + x) + (10x + y) = 110
⇒ 11x + 11y = 110
⇒ x + y – 10 = 0
Again, according to question, we have
(10y + x) – 10 = 5 (x + y) + 4
⇒ 10y + x – 10 = 5x + 5y + 4
⇒ 10y + x – 5x – 5y = 4 + 10
5y – 4x = 14 or 4x – 5y + 14 = 0
By using cross-multiplication, we have .
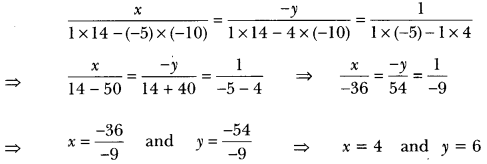
Putting the values of x and y in equation (i), we get
Number 10 × 6 + 4 = 64.
Question 11.
Jamila sold a table and a chair for 1050, thereby making a profit of 10% on the table and 25% on the chair. If she had taken a profit of 25% on the table and 10% on the chair she would have got 1065. Find cost price of each.
Solution:
Let cost price of table be ₹x and the cost price of the chair be ₹y.
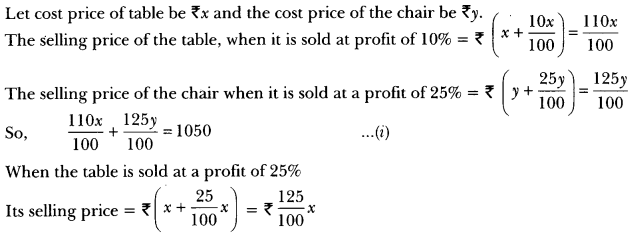 ”
”
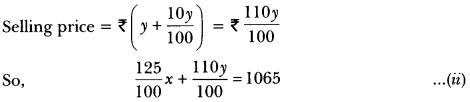
From equation (i) and (ii) we get
110x + 125y = 105000
and 125x + 110y = 106500
On adding and subtracting these equations, we get
235x + 235y = 211500
and 15x – 15y = 1500
i.e., x + y = 900 …(iii)
x – y = 100 …… (iv)
Solving equation (iii) and (iv) we get
x = 500, y = 400
So, the cost price of the table is ₹500 and the cost price of the chair is ₹400.
Pair of Linear Equations in Two Variables Class 10 Extra Questions HOTS
Question 1.
8 men and 12 boys can finish a piece of work in 10 days while 6 men and 8 boys can finish it in 14 days. Find the time taken by one man alone and that by one boy alone to finish the work.
Solution:
Let one man alone can finish the work in x days and one boy alone can finish the work in y days
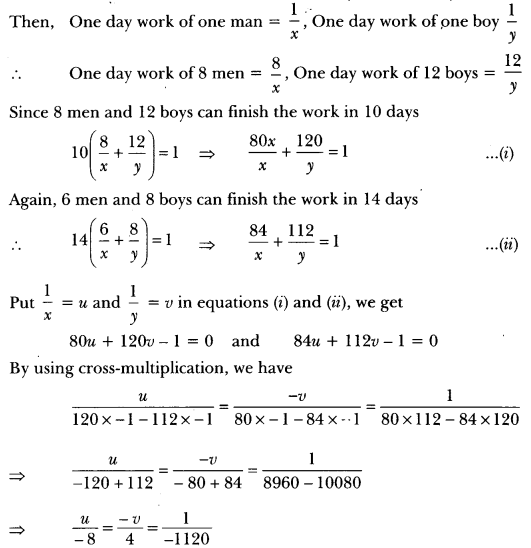
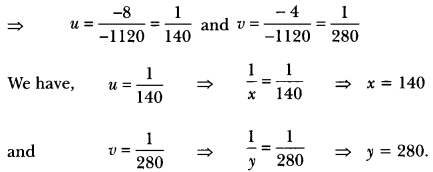
Hence, one man alone can finish the work in 140 days and one boy alone can finish the work in 280 days.
Question 2.
A boat covers 25 km upstream and 44 km downstream in 9 hours. Also, it covers 15 km upstream and 22 km downstream in 5 hours. Find the speed of the boat in still water and that of the stream.
Solution:
Let the speed of the boat in still water be x km/h and that of the stream be y km/h. Then,
Speed upstream (x – y) km/h
Speed downstream (x + y) km/h
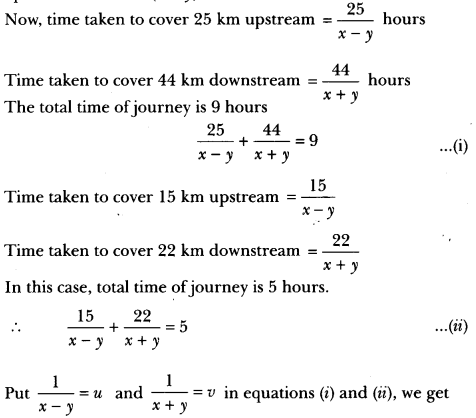
25u + 44v = 9 ⇒ 25u + 44v – 9 = 0 …(iii)
15u + 22v = 5 ⇒ 15u + 22v – 5 = 0 …(iv)
By cross-multiplication, we have
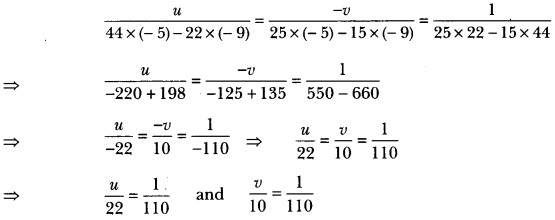
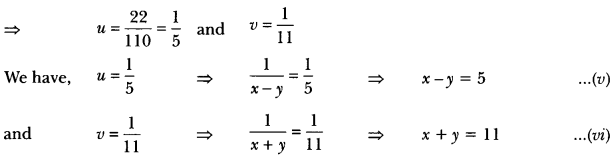
Solving equations (v) and (vi), we get x = 8 and y = 3.
Hence, speed of the boat in still water is 8 km/h and speed of the stream is 3 km/h.
Question 3.
Students of a class are made to stand in rows. If one student is extra in each row, there would be 2 rows less. If one student is less in each row, there would be 3 rows more. Find the number of students in the class.
Solution:
Let total number of rows be y
and total number of students in each row be x – Total number of students = xy
Case I: If one student is extra in each row, there would be two rows less. Now, number of rows = (y-2) Number of students in each row = (x + 1)
Total number of students = Number of rows x Number of students in each row
xy = 6 – 2)(x + 1) ⇒ xy = xy + y – 2x – 2
xy – xy – y + 2x = -2 ⇒ 2x – y = -2 …(i)
Case II: If one student is less in each row, there would be 3 rows more.
Now, number of rows = (y + 3)
and number of students in each row = (x – 1)
Total number of students = Number of rows x Number of students in each row
∴ xy = 6 + 3)(x – 1) ⇒ xy = xy – y + 3x – 3
xy – xy + y – 3x = -3 ⇒ – 3x + y = -3 … (ii)
On adding equations (i) and (ii), we have
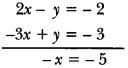
or
Putting the value of x in equation (i), we get
2(5) – y = -2
⇒ 10- y = -2
– y = -2 – 10
⇒ – y = -12
or y = 12
∴ Total number of students in the class = 5 × 12 = 60.
Question 4.
Draw the graph of 2x + y = 6 and 2x – y + 2 = 0. Shade the region bounded by these lines and x-axis. Find the area of the shaded region.
Solution:
We have, 2x + y = 6, ⇒ y = 6 – 2x
When x = 0, we have y = 6 – 2 × 0 = 6
When x = 3, we have y = 6 – 2 × 3 = 0
When x = 2, we have y = 6 – 2 × 2 = 2
Thus, we get the following table:

Now, we plot the points A(0,6), B(3,0) and C(2, 2) on the graph paper. We join A, B and C and extend it on both sides to obtain the graph of the equation 2x + y = 6.
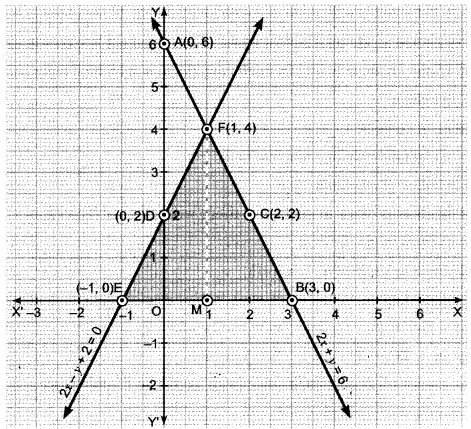
We have, 2x – y + 2 = 1 = y = 2x + 2
When x = 0, we have y = 2 × 0 + 2 = 2
When x = -1, we have y = 2 × (-1) + 2 = 0
When x = 1, we have y = 2 × 1 + 2 = 4
Thus, we have the following table:

Now, we plot the points D(0, 2), E(-1,0) and F(1,4) on the same graph paper. We join D, E and F and extend it on both sides to obtain the graph of the equation 2x – y + 2 = 0. It is evident from the graph that the two lines intersect at point F(1,4). The area enclosed by the given lines and x-axis is shown in Fig. 3.7.
Thus, x = 1, y = 4 is the solution of the given system of equations. Draw FM perpendicular from Fon x-axis.
Clearly, we have
FM = y-coordinate of point F(1, 4) = 4 and BE = 4
∴ Area of the shaded region = Area of AFBE
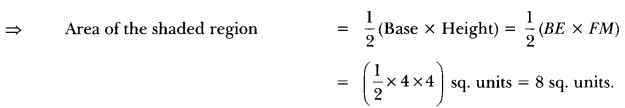
Question 5.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Solution:
Let the ages of Ani and Biju be x and y years respectively. Then x – y = 13
Age of Dharam = 2x years
Age of Cathy = \(\frac{y}{2}\) years
Clearly, Dharam is older than Cathy
IMMM
Thus, we have following two systems of linear equations
x – y = 3 ….. (i)
4x – y = 60 … (ii)
and x – y = -3 … (iii)
4x – y = 60 … (iv)
Subtracting equation (i) from (ii), we get
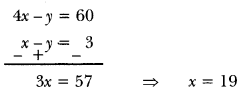
Putting x = 19 in equation (i), we get
19 – y = 3 ⇒ y = 16
Now, subtracting equation (iii) from (iv)
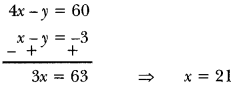
Putting x = 21 in equation (iii), we get
21 – y = -3 ⇒ y = 24
Hence, age of Ani = 19 years and age of Biju = 16 years
or age of Ani = 21 years and age of Biju = 24 years
Question 6.
A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h it would have taken 3 hours more than the scheduled time. Find distance covered by the train.
Solution:
Let actual speed of the train be x km/h and actual time taken be y hours.
Then, distance covered = speed × time = xy km … (i)
Case I: When speed is (x + 10) km/h, then time taken is (y – 2) hours
∴ Distance covered = (x + 10)(y – 2)
⇒ xy = (x + 10)(y – 2) [From (i)]
= xy = xy – 2x + 10y – 20 ⇒ 2x – 10y = -20 ….(ii)
⇒ x – 5y = -10
Case II: When speed is (x – 10) km/h, then time taken is (y + 3) hours.
∴Distance covered = (x – 10)(y + 3)
xy = (x – 10)(y + 3) [From (i)]
xy = xy + 3x – 10y – 30 …..(iii)
= 3x – 10y = 30
Multiplying equation (ii) by 2 and subtracting it from (iii), we get
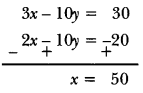
Putting x = 50 in equation (ii), we get
50 – 5y = -10
⇒ 50 + 10 = 5y ⇒ y = 12
∴ Distance covered by the train = xy km = 50 × 12 km = 600 km