Class 6 Maths Chapter 3 Extra Questions Number Play
Class 6 Maths Number Play Extra Questions
NCERT Class 6 Maths Chapter 3 Number Play Extra Questions and Answers
Very Short Answer Type
Question 1.
Mark the supercells in the table given below.
Answer:
Question 2.
Fill in the table below with only 3-digit numbers such that the supercells are exactly the circled cell.
Answer:
Question 3.
Mark the supercells in the table given below.
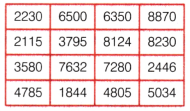
Answer:
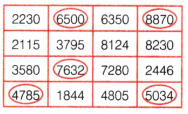
Question 4.
Which one is the greatest number?
(i) 47645, 48740
(ii) 15896, 26760
Answer:
(i) Here, ten thousands digit is 4 in both numbers.
But thousands digit in 47645 is 7 and thousands digit in 48740 is 8. So, 8 > 7.
Hence, 48740 > 47645
(ii) In 15896, ten thousands digit is 1 and ten thousands digit in 26760 is 2. So, 2 > 1.
Hence, 26760 > 15896.
Question 5.
Write the greatest and smallest of the following numbers, 29706, 28706, 39406, 87604.
Answer:
In the given numbers, we see that 28706 is the smallest and 87604 is the greatest.
Question 6.
Using the digits 3, 5, 4, 6 without repetition, write the smallest four digit number.
Answer:
Here, given digits are 3, 5, 4, 6. For the smallest number, we write the digits in ascending order. So, the smallest four digit number is 3456.
Question 7.
Make the greatest five digit number using the digits 1, 2, 7, 9,4, without repetition.
Answer:
Given, digits are 1, 2, 7, 9, 4.
For greatest number, we write the digits in descending order.
So, the greatest five-digit number is 97421.
Question 8.
What is the first step of the Collatz conjecture for an even number.
Answer:
The first step of the Collatz conjecture for an even number is to divide the number by 2.
Question 9.
What is the smallest four digit palindrome number?
Answer:
Smallest four-digit palindrome number is 1001.
Question 10.
What is the result when you repeately apply the Kaprekar routine to the number 3524?
Answer:
The result is 6174.
Question 11.
What is the sum of the digits in the number 909 and 666?
Answer:
The sum is 9 + 0 + 9 =18, 6 + 6 + 6 = 18
Question 12.
Is 78987 a palindromic number?
Answer:
Yes, 78987 is a palindromic number.
Question 13.
How many numbers are there between 10 and 20 in the pattern increasing by 2? Competency Based Question
Answer:
We have the pattern as 10, 12, 14, 16, 18, 20
Thus, there are four numbers between 10 and 20.
Short Answer Type Questions
Question 1.
Identify the numbers marked on the number lines below, and label the remaining positions.
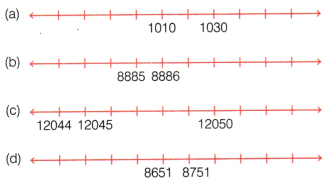
Answer:
Question 2.
Put a circle around the smallest number and a box around the largest number in each of the above sequences in question 1.
Answer:
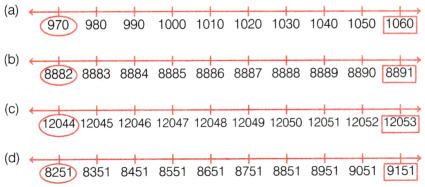
Question 3.
What is the next number in the Collatz sequence after 8?
Answer:
Since, 8 is an even number, the next number in the Collatz sequence will be half of 8 i.e. 4.
Question 4.
If you start with 7, then what is the result of the Collatz Sequence?
Answer:
If we start with 7, the result of the Collatz sequence is
7 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1.
Question 5.
Use the numbers, 50000, 800, 500, 300 and 1200 to form the number 49800.
Answer:
50000 -1200 – 300 + 800 + 500 = 49800
Question 6.
What is the largest five digit palindrome number?
Answer:
The largest five digit nalindrome number is 99999.
Question 7.
What happens to the number 11 in the Collatz conjecture?
Answer:
Since, 11 is an odd number, we multiply 11 by 3 and then add 1 to it.
i.e. 11 x 3 + 1 = 34
Question 8.
Identify the supercells in the given table.
Answer:
Question 9.
Complete the number line given below.
Answer:
Question 10.
Write two 3-digit numbers whose digits sum is 20.
Answer:
3-digits numbers whose digit’s sum 20 are 992(9 + 9 + 2 = 20) and 965(9 + 6 + 5 = 20).
Question 11.
What is the next number in the Collatz sequence after 15?
Answer:
Since, 15 is an odd number.
We multiply 15 by 3 and then add 1 to it. i.e. 15 × 3 + 1 =46
Question 12.
What is the difference largest and smallest four digit number made by using digits 4, 6, 8, 1.
Answer:
Largest Number = 8641
Smallest Number = 1468
Difference = 8641 – 1468 = 7173
Long Answer Type Questions
Question 1.
Mark the supercells in the given table and write the reason behind it.
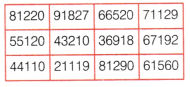
Answer:
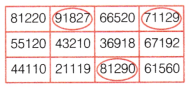
Since, the numbers adjacent to 91827, 71129 and 81290 are smaller, therefore these numbers are supercells.
Question 2.
Choose four digits to make Competency Based Question
(a) the difference between the largest and smallest numbers greater than 4045.
(b) the difference between the largest and smallest number less than 5085.
(c) the sum of the largest and smallest numbers greater than 6556.
(d) the sum of the largest and smallest numbers less than 6556.
Answer:
(a) Largest number = 9999 and smallest number = 4046
Difference = 5953
(b) Largest number = 5084 and smallest number = 1000
Difference = 4084
(c) Largest number = 9999 and smallest number = 6557
Sum = 16556
(d) Largest number = 6555 and smallest = 1000
Sum =7555
Question 3.
Write an example for each of the following scenarios.
(i) 5-digit + 5-digit to give a 5-digit sum more than 50550.
(ii) 5-digit + 5-digit to give 28500.
(iii) 4-digit + 4-digit to give a 5-digit sum.
(iv) 5-digit – 5-digit to give 61600.
(v) 5-digit + 3-digit to give a 6-digit sum.
(vi) 5-digit -4-digit to give 4-digit difference.
(vii) 5-digit -5-digit to give a 3-digit difference.
Answer:
(i) 55000 + 12000=67000
(ii) 17500+11000 = 28500
(iii) 9999+1100=11099
(iv) 99999-38399=61600
(v) 99999+999=100998
(vi) 10000-2000 = 8000
(vii) 90000-89500 = 500
Question 4.
Apply the Kaprekar routine to the number 1225, show each step and verify if the routine leads to Kaprekar! constant.
Answer:
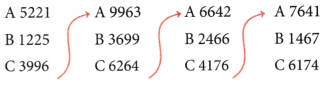
Thus, we obtain Kaprekar’s constant 6174.
Question 5.
What is the sum of the smallest and largest four digit palindrome? What is their difference?
Answer:
Smallest 4-digit palindrome number = 1001
Largest 4-digit palindrome number = 9999
Difference = 9999-1001 = 8998
Sum = 9999 + 1001 = 11000
Question 6.
Identify the pattern in the sequence 2218, 2220, 2222, 2224.
Explain how would you find the next three numbers in the given sequence.
Answer:
In the sequence,
2218, 2220, 2222, 2224,…
The next number is two more than the previous number.
Thus, next three numbers are
2224 + 2 = 2226
2226 + 2 = 2228
2228 + 2 = 2230
Question 7.
Write an example for the following
(i) 5-digit – 5-digit to give 61500
(ii) 4-digit + 4-digit to give a 5-digit sum
Answer:
(i) The two 5-digit numbers whose difference is
81500 – 20000 = 61500
(ii) 9843 + 1024 = 10867
Question 8.
Show the Collatzsequence starting with number 12.
Answer:
12 (even) → (12/2 = 6)
6 (even) → (6/2 = 3)
3 (odd) → (3 × 3 + 1= 10)
10 (even) →(10 / 2 = 5)
5 (odd) → (5 × 3 + 1 = 16)
16 (even) → (16/2 = 8)
8 (even) → (8/2 = 4)
4 (even) → (4/2 = 2)
2 (even) → (2 / 2 = 1)
So, the Collatz sequence for 12 is 12, 6, 3, 10, 5, 16, 8, 4, 2, 1.
Case Study-based Questions
Question 1.
Sita and Raj are exploring giant number lines in their playground. They start at the number 5 and hopes to different numbers following specific rules. Sita hopes three numbers ahead, while Raj hopes two numbers back.
Based on the above information, answer the following questions.
(i) If Sita starts at 5 and hopes 3 numbers ahead, where does she land?
(ii) If Raj starts at 5 and hopes 2 numbers back, where does he land?
(iii) What is the sum of the numbers where Sita and Raj lands.
Answer:
(i) 5 + 3 = 8
(ii) 5-2 = 3
(iii) 8 + 3 = 11
Question 2.
A student has the digits 5, 5,1, and 2. The task is to form both the smallest and largest four digit numbers using these digits.
Based on the above information, answer the following questions.
(i) What is the smallest number you can form using the digits 5, 5,1, and 2
(ii) What is the largest number you can form using these same digits?
(iii) What is the sum of the largest and the smallest numbers so formed?
(iv) What is the difference between the smallest and the largest numbers so formed?
Answer:
(i) 1255
(ii) 5521
(iii) 1255 + 5521 = 6776
(iv) 5521 – 1255 = 4266
Question 3.
A teacher shows the students some numbers on the number line. She asks the students to identify the pattern and predict the numbers on the number line.
Based on the above information, answer the following questions.
(i) What is the pattern in the given number line?
(ii) What is the 6th number on the number line?
(iii) Write down all the numbers on the number line.
Answer:
(i) There is a difference of 1000 between each consecutive numbers.
(ii) 26650
(iii)
