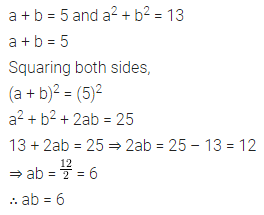ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Check Your Progress
Question 1.
Add the following expressions:
(i) -5x2y + 3xy2 – 7xy + 8, 12x2y – 5xy2 + 3xy – 2
(ii) 9xy + 3yz – 5zx, 4yz + 9zx – 5y, -5xz + 2x – 5xy
Solution:
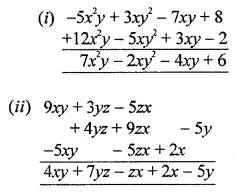
Question 2.
Subtract:
(i) 5a + 3b + 11c – 2 from 3a + 5b – 9c + 3
(ii) 10x2 – 8y2 + 5y – 3 from 8x2 – 5xy + 2y2 + 5x – 3y
Solution:
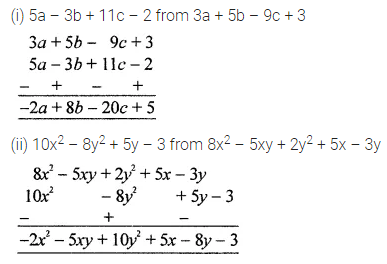
Question 3.
What must be added to 5x2 – 3x + 1 to get 3x3 – 7x2 + 8?
Solution:
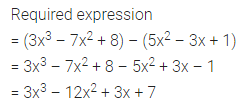
Question 4.
Find the product of
(i) 3x2y and -4xy2
(ii) –\(\frac{4}{5}\)xy, \(\frac{5}{7}\)yz and –\(\frac{14}{9}\)zx
Solution:
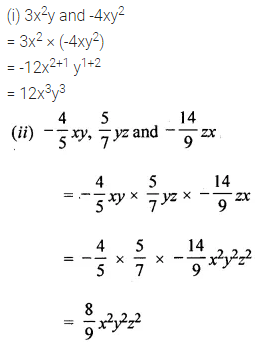
Question 5.
Multiply:
(i) (3pq – 4p2 + 5q2 + 7) by -7pq
(ii) (\(\frac{3}{4}\)x2y – \(\frac{4}{5}\)xy + \(\frac{5}{6}\)xy2) by – 15xyz
Solution:
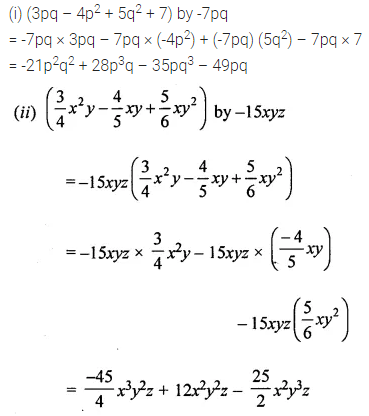
Question 6.
Multiply:
(i) (5x2 + 4x – 2) by (3 – x – 4x2)
(ii) (7x2 + 12xy – 9y2) by (3x2 – 5xy + 3y2)
Solution:
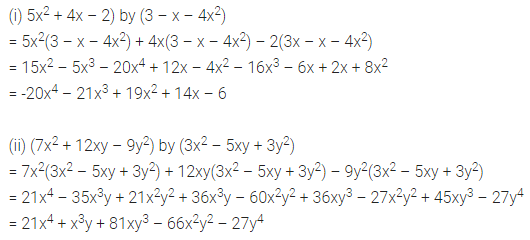
Question 7.
Simplify the following expressions and evaluate them as directed:
(i) (3ab – 2a2 + 5b2) x (2b2 – 5ab + 3a2) + 8a3b – 7b4 for a = 1, b = -1
(ii) (1.7x – 2.5y) (2y + 3x + 4) – 7.8x2 – 10y for x = 0, y = 1.
Solution:
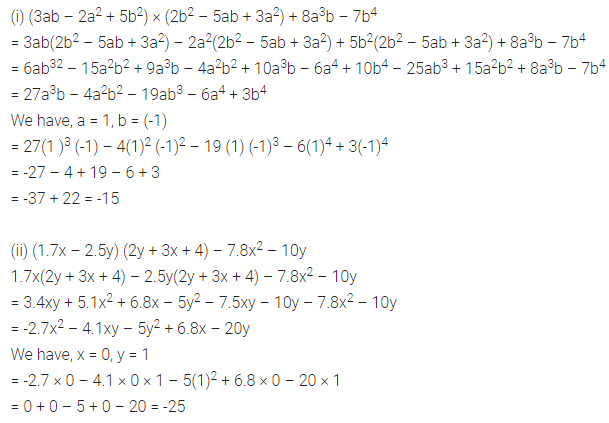
Question 8.
Carry out the following divisions:
(i) 66pq2r3 ÷ 11qr2
(ii) (x3 + 2x2 + 3x) ÷ 2x
Solution:
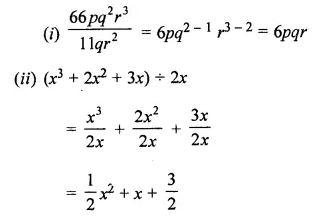
Question 9.
Divide 10x4 – 19x3 + 17x2 + 15x – 42 by 2x2 – 3x + 5.
Solution:

Question 10.
Using identities, find the following products:
(i) (3x + 4y) (3x + 4y)
(ii) \(\left(\frac{5}{2} a-b\right)\left(\frac{5}{2} a-b\right)\)
(iii) (3.5m – 1.5n) (3.5m + 1.5n)
(iv) (7xy – 2)(7xy + 7)
Solution:
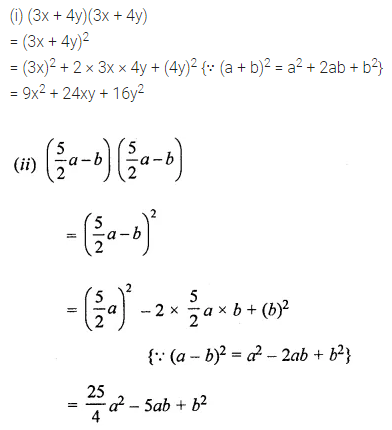
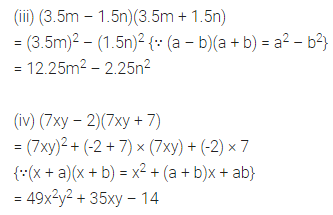
Question 11.
Using suitable identities, evaluate the following:
(i) 1052
(ii) 972
(iii) 201 × 199
(iv) 872 – 132
(v) 105 × 107
Solution:
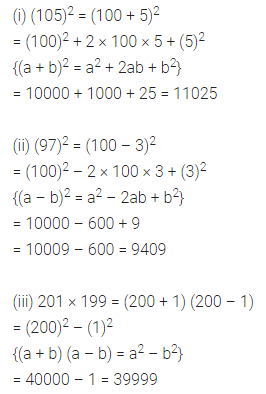
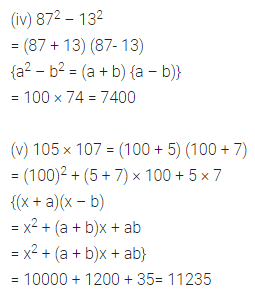
Question 12.
Prove that following:
(i) (a + b)2 – (a – b)2 + 4ab
(ii) (2a + 3b)2 + (2a – 3b)2 = 8a2 + 18b2
Solution:
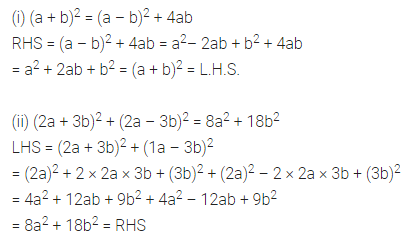
Question 13.
If x + \(\frac{1}{x}\) = 5, evaluate

Solution:
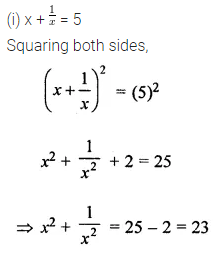
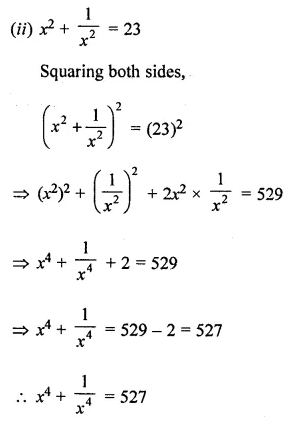
Question 14.
If a + b = 5 and a2 + b2 = 13, find ab.
Solution: