Here we are providing Lines and Angles Class 9 Extra Questions Maths Chapter 6 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers.
Extra Questions for Class 9 Maths Lines and Angles with Answers Solutions
Extra Questions for Class 9 Maths Chapter 6 Lines and Angles with Solutions Answers
Lines and Angles Class 9 Extra Questions Very Short Answer Type
Question 1.
If an angle is half of its complementary angle, then find its degree measure.
Solution:
Let the required angle be x
∴ Its complement = 90° – x
Now, according to given statement, we obtain
x = \(\frac{1}{2}\)(90° – x)
⇒ 2x = 90° – x
⇒ 3x = 90°
⇒ x = 30°
Hence, the required angle is 30°.
Question 2.
The two complementary angles are in the ratio 1 : 5. Find the measures of the angles.
Solution:
Let the two complementary angles be x and 5x.
∴ x + 5x = 90°
⇒ 6x = 90°
⇒ x = 15°
Hence, the two complementary angles are 15° and 5 × 15° i.e., 15° and 75°.
Question 3.
In the given figure, if PQ || RS, then find the measure of angle m.
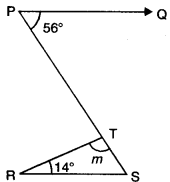
Solution:
Here, PQ || RS, PS is a transversal.
⇒ ∠PSR = ∠SPQ = 56°
Also, ∠TRS + m + ∠TSR = 180°
14° + m + 56° = 180°
⇒ m = 180° – 14 – 56 = 110°
Question 4.
If an angle is 14o more than its complement, then find its measure.
Solution:
Let the required angle be x
∴ Its complement = 90° – x
Now, according to given statement, we obtain
x = 90° – x + 14°
⇒ 2x = 104°
⇒ x = 52°
Hence, the required angle is 52o.
Solving the variable value in an arithmetic equation is not difficult anymore with our free online find the Value of X Calculator tool.
Question 5.
If AB || EF and EF || CD, then find the value of x.
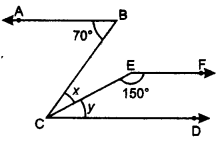
Solution:
Since EF || CD ∴ y + 150° = 180°
⇒ y = 180° – 150° = 30°
Now, ∠BCD = ∠ABC
x + y = 70°
x + 30 = 70
⇒ x = 70° – 30° = 40°
Hence, the value of x is 40°.
Question 6.
In the given figure, lines AB and CD intersect at O. Find the value of x.
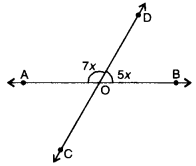
Solution:
Here, lines AB and CD intersect at O.
∴ ∠AOD and ∠BOD forming a linear pair
⇒ ∠AOD + ∠BOD = 180°
⇒ 7x + 5x = 180°
⇒ 12x = 180°
⇒ x = 15°
Question 7.
In the given figure, PQ || RS and EF || QS. If ∠PQS = 60°, then find the measure of ∠RFE.
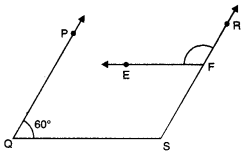
Solution:
Since PQ || RS
∴ ∠PQS + ∠QSR = 180°
⇒ 60° + ∠QSR = 180°
⇒ ∠QSR = 120°
Now, EF || QS ⇒ ∠RFE = ∠QSR [corresponding ∠s]
⇒ ∠RFE = 120°
Question 8.
In the given figure, if x°, y° and z° are exterior angles of ∆ABC, then find the value of x° + y° + z°.
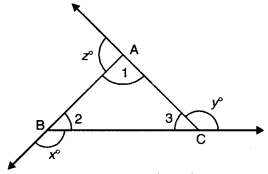
Solution:
We know that, an exterior angle of a triangle is equal to sum of two opposite interior angles.
⇒ x° = ∠1 + ∠3
⇒ y° = ∠2 + ∠1
⇒ z° = ∠3 + ∠2
Adding all these, we have
x° + y° + z° = 2(∠1 + ∠2 + ∠3)
= 2 × 180°
= 360°
Lines and Angles Class 9 Extra Questions Short Answer Type 1
Question 1.
In the given figure, AB || CD, ∠FAE = 90°, ∠AFE = 40°, find ∠ECD.
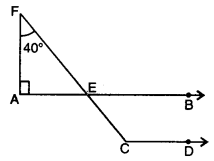
Solution:
In AFAE,
ext. ∠FEB = ∠A + F
= 90° + 40° = 130°
Since AB || CD
∴ ∠ECD = FEB = 130°
Hence, ∠ECD = 130°.
Question 2.
In the fig., AD and CE are the angle bisectors of ∠A and ∠C respectively. If ∠ABC = 90°, then find ∠AOC.
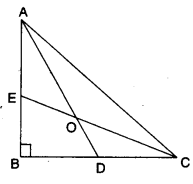
Solution:
∵ AD and CE are the bisector of ∠A and ∠C

In ∆AOC,
∠AOC + ∠OAC + ∠OCA = 180°
⇒ ∠AOC + 45o = 180°
⇒ ∠AOC = 180° – 45° = 135°.
Question 3.
In the given figure, prove that m || n.
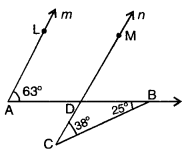
Solution:
In ∆BCD,
ext. ∠BDM = ∠C + ∠B
= 38° + 25° = 63°
Now, ∠LAD = ∠MDB = 63°
But, these are corresponding angles. Hence,
m || n
Question 4.
In the given figure, two straight lines PQ and RS intersect each other at O. If ∠POT = 75°, find the values of a, b, c.
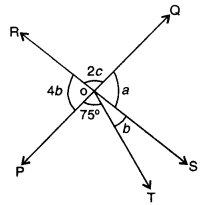
Solution:
Here, 4b + 75° + b = 180° [a straight angle]
5b = 180° – 75° = 105°
b – \(\frac{105^{\circ}}{5}\) = 21°
∴ a = 4b = 4 × 21° = 84° (vertically opp. ∠s]
Again, 2c + a = 180° [a linear pair]
⇒ 2c + 84° = 180°
⇒ 2c = 96°
⇒ c = \(\frac{96^{\circ}}{2}\) = 48°
Hence, the values of a, b and c are a = 84°, b = 21° and c = 48°.
Question 5.
In figure, if AB || CD. If ∠ABR = 45° and ∠ROD = 105°, then find ∠ODC.
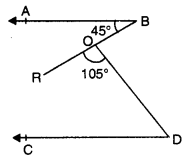
Solution:
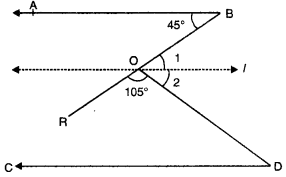
Through O, draw a line ‘l’ parallel to AB.
⇒ line I will also parallel to CD, then
∠1 = 45°[alternate int. angles]
∠1 + ∠2 + 105° = 180° [straight angle]
∠2 = 180° – 105° – 45°
⇒ ∠2 = 30°
Now, ∠ODC = ∠2 [alternate int. angles]
= ∠ODC = 30°
Question 6.
In the figure, ∠X = 72°, ∠XZY = 46°. If YO and ZO are bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OYZ and ∠YOZ.
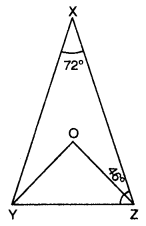
Solution:
In ∆XYZ, we have
∠X + XY + ∠Z = 180°
⇒ ∠Y + ∠Z = 180° – ∠X
⇒ ∠Y + ∠Z = 180° – 72°
⇒ Y + ∠Z = 108°
⇒ \(\frac{1}{2}\) ∠Y + \(\frac{1}{2}\)∠Z = \(\frac{1}{2}\) × 108°
∠OYZ + ∠OZY = 54°
[∵ YO and ZO are the bisector of ∠XYZ and ∠XZY]
⇒ ∠OYZ + \(\frac{1}{2}\) × 46° = 54°
∠OYZ + 23° = 54°
⇒ ∠OYZ = 549 – 23° = 31°
In ∆YOZ, we have
∠YOZ = 180° – (∠OYZ + ∠OZY)
= 180° – (31° + 23°) 180° – 54° = 126°
Lines and Angles Class 9 Extra Questions Short Answer Type 2
Question 1.
Prove that if two lines intersect each other, then the bisectors of vertically opposite angles are in the same line.
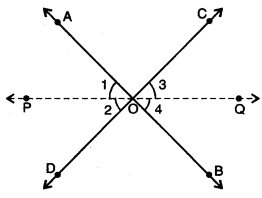
Solution:
Let AB and CD be two intersecting lines intersecting each other in O.
OP and OQ are bisectors of ∠AOD and ∠BOC.
∴ ∠1 = ∠2 and ∠3 = ∠4 …(i)
Now, ∠AOC = ∠BOD [vertically opp. ∠s] ……(ii)
⇒ ∠1 + ∠AOC + ∠3 = ∠2 + ∠BOD + ∠4 [adding (i) and (ii)]
Also, ∠1 + ∠AOC + ∠3 + ∠2 + ∠BOD + ∠4 = 360° (∵ ∠s at a point are 360°]
⇒ ∠1 + ∠AOC + ∠3 + ∠1 + ∠AOC + ∠3 = 360° [using (i), (ii)]
⇒ ∠1 + ∠AOC + ∠3 = 180°
or ∠2 + ∠BOD + ∠4 = 180°
Hence, OP and OQ are in the same line.
Question 2.
In figure, OP bisects ∠BOC and OQ bisects ∠AOC. Prove that ∠POQ = 90°
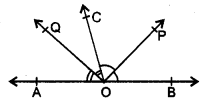
Solution:
∵ OP bisects ∠BOC
∴ ∠BOP = ∠POC = x (say)
Also, OQ bisects. ∠AOC
∠AOQ = ∠COQ = y (say) .
∵ Ray OC stands on ∠AOB
∴ ∠AOC + ∠BOC = 180° [linear pair]
⇒ ∠AOQ + ∠QOC + ∠COP + ∠POB = 180°
⇒ y + y + x + x = 180°.
⇒ 2x + 2y = 180°
⇒ x + y = 90°
Now, ∠POQ = ∠POC + ∠COQ
= x + y = 90°
Question 3.
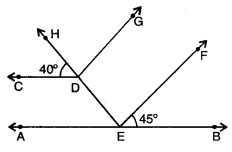
In given figure, AB || CD and EF || DG, find ∠GDH, ∠AED and ∠DEF.
Solution:
Since AB || CD and HE is a transversal.
∴ ∠AED = ∠CDH = 40° [corresponding ∠s]
Now, ∠AED + ∠DEF + ∠FEB = 180° [a straight ∠]
40° + CDEF + 45° = 180°
∠DEF = 180° – 45 – 40 = 95°
Again, given that EF || DG and HE is a transversal. .
∴ ∠GDH = ∠DEF = 95° [corresponding ∠s]
Hence, ∠GDH = 95°, ∠AED = 40° and ∠DEF = 95°
Question 4.
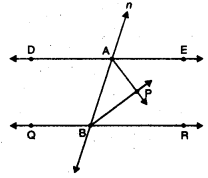
In figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA respectively. Find ∠APB.
Solution:
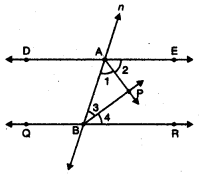
Here, AP and BP are bisectors of ∠EAB and ∠RBA respectively.
⇒ ∠1 = ∠2 and ∠3 = ∠4
Since DE || QR and transversal n intersects DE and QR at A and B respectively.
⇒ ∠EAB + ∠RBA = 180°
[∵ co-interior angles are supplementary]
⇒ (∠1 + ∠2) + (∠3 + ∠4) = 180°
⇒ (∠1 + ∠1) + (∠3 + ∠3) = 180° (using (i)
⇒ 2(∠1 + ∠3) = 180°
⇒ ∠1 + ∠3 = 90°
Now, in ∆ABP, by’angle sum property, we have
∠ABP + ∠BAP + ∠APB = 180°
⇒ ∠3 + ∠1 + ∠APB = 180°
⇒ 90° + ∠APB = 180°
⇒ ∠APB = 90°
Question 5.
In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).
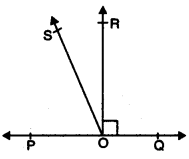
Solution:
Given that OR is perpendicular to PQ
⇒ ∠POR = ∠ROQ = 90°
∴ ∠POS + ∠ROS = 90°
⇒ ∠ROS = 90° – ∠POS
Adding ∠ROS to both sides, we have
∠ROS + ∠ROS = (90° + ∠ROS) – ∠POS
⇒ 2∠ROS = ∠QOS – ∠POS
⇒ ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).
Question 6 .
If two parallel lines are intersected by a transversal, then prove that the bisectors of any two corresponding angles are parallel.
Solution:
Given : AB || CD and transversal PQ meet these lines at E and F respectively. EG and FH are
the bisectors of pair of corresponding angles ∠PEB and ∠EFD.
To Prove : EG || FH Proof
∵ EG and FH are bisectors of ∠PEB respectively.
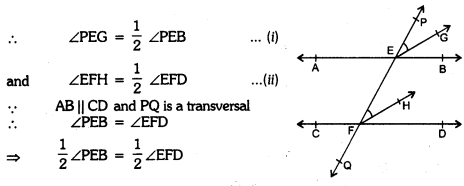
∠PEG = ∠EFH
Which are corresponding angles of EG and FH
∴ EG || FH.
Question 7.
In the given figure, m and n are two plane mirrors perpendicular to each other. Show that incident rays CA is parallel to reflected ray BD.
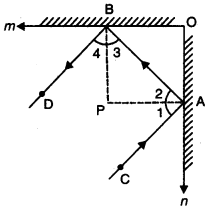
Solution:
Let normals at A and B meet at P.
As mirrors are perpendicular to each other, therefore, BP || OA and AP || OB.
So, BP ⊥ PA i.e., ∠BPA = 90°
Therefore, ∠3 + ∠2 = 90° [angle sum property] …(i)
Also, ∠1 = ∠2 and ∠4 = ∠3 [Angle of incidence = Angle of reflection]
Therefore, ∠1 + ∠4 = 90° [from (i)) …(ii]
Adding (i) and (ii), we have
∠1 + ∠2 + ∠3 + ∠4 = 180°
i.e., ∠CAB + ∠DBA = 180°
Hence, CA || BD
Lines and Angles Class 9 Extra Questions Long Answer Type
Question 1.
If two parallel lines are intersected by a transversal, prove that the bisectors of two pairs of interior angles form a rectangle.
Solution:
Given : AB || CD and transversal EF cut them at P and Q respectively and the bisectors of
pair of interior angles form a quadrilateral PRQS.
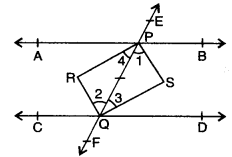
To Prove : PRQS is a rectangle.
Proof : ∵ PS, QR, QS and PR are the bisectors of angles
∠BPQ, ∠CQP, ∠DQP and ∠APQ respectively.
∴∠1 =\(\frac{1}{2}\) ∠BPQ, ∠2 = \(\frac{1}{2}\)∠CQP,
∠3 = \(\frac{1}{2}\)∠DQP and ∠4 = \(\frac{1}{2}\)∠APQ
Now, AB || CD and EF is a transversal
∴ ∠BPQ = ∠CQP
⇒ ∠1 = ∠2 (∵∠1 \(\frac{1}{2}\) ∠BPQ and ∠2 = \(\frac{1}{2}\)∠QP)
But these are pairs of alternate interior angles of PS and QR
∴ PS || QR
Similarly, we can prove ∠3 = ∠4 = QS || PR
∴ PRQS is a parallelogram.
Further ∠1 + ∠3 = \(\frac{1}{2}\)∠BPQ + \(\frac{1}{2}\)∠DQP = \(\frac{1}{2}\) (∠BPQ + ∠DQP)
= \(\frac{1}{2}\) × 180° = 90° (∵ ∠BPQ + ∠DQP = 180°)
∴ In ∆PSQ, we have ∠PSQ = 180° – (∠1 + ∠3) = 180° – 90° = 90°
Thus, PRRS is a parallelogram whose one angle ∠PSQ = 90°.
Hence, PRQS is a rectangle.
Question 2.
If in ∆ABC, the bisectors of ∠B and ∠C intersect each other at O. Prove that ∠BOC = 90° + \(\frac{1}{2}\)∠ A.
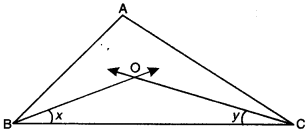
Solution:
Let ∠B = 2x and ∠C = 2y
∵OB and OC bisect ∠B and ∠C respectively.
∠OBC = \(\frac{1}{2}\)∠B = \(\frac{1}{2}\) × 2x = x
and ∠OCB = \(\frac{1}{2}\)∠C = \(\frac{1}{2}\) × 2y = y
Now, in ∆BOC, we have
∠BOC + ∠OBC + ∠OCB = 180°
⇒ ∠BOC + x + y = 180°
⇒ ∠BOC = 180° – (x + y)
Now, in ∆ABC, we have
∠A + 2B + C = 180°
⇒ ∠A + 2x + 2y = 180°
⇒ 2(x + y) = \(\frac{1}{2}\)(180° – ∠A)
⇒ x + y = 90° – \(\frac{1}{2}\)∠A …..(ii)
From (i) and (ii), we have
∠BOC = 180° – (90° – \(\frac{1}{2}\)∠A) = 90° + \(\frac{1}{2}\) ∠A
Question 3.
In figure, if I || m and ∠1 = (2x + y)°, ∠4 = (x + 2y)° and ∠6 = (3y + 20)°. Find ∠7 and ∠8.
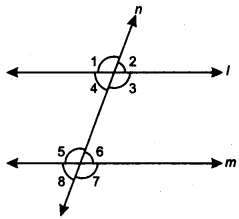
Solution:
Here, ∠1 and ∠4 are forming a linear pair
∠1 + ∠4 = 180°
(2x + y)° + (x + 2y)° = 180°
3(x + y)° = 180°
x + y = 60
Since I || m and n is a transversal
∠4 = ∠6
(x + 2y)° = (3y + 20)°
x – y = 20
Adding (i) and (ii), we have
2x = 80 = x = 40
From (i), we have
40 + y = 60 ⇒ y = 20
Now, ∠1 = (2 x 40 + 20)° = 100°
∠4 = (40 + 2 x 20)° = 80°
∠8 = ∠4 = 80° [corresponding ∠s]
∠1 = ∠3 = 100° [vertically opp. ∠s]
∠7 = ∠3 = 100° [corresponding ∠s]
Hence, ∠7 = 100° and ∠8 = 80°
Question 4.
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28o and ∠QRT = 65°. Find the values of x, y and z.
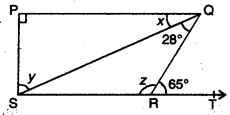
Solution:
Here, PQ || SR .
⇒ ∠PQR = ∠QRT
⇒ x + 28° = 65°
⇒ x = 65° – 28° = 37°
Now, in it. ∆SPQ, ∠P = 90°
∴ ∠P + x + y = 180° [angle sum property]
∴ 90° + 37° + y = 180°
⇒ y = 180° – 90° – 37° = 53°
Now, ∠SRQ + ∠QRT = 180° [linear pair]
z + 65° = 180°
z = 180° – 65° = 115°
Question 5.
In figure, AP and DP are bisectors of two adjacent angles A and D of a quadrilateral ABCD. Prove that 2∠APD = ∠B + ∠C.
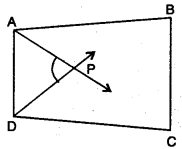
Solution:
In quadrilateral ABCD, we have
∠A + ∠B.+ ∠C + ∠D = 360°

Question 6.
In figure, PS is bisector of ∠QPR ; PT ⊥ RQ and Q > R. Show that ∠TPS = \(\frac{1}{2}\)(∠Q – ∠R).
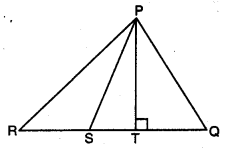
Solution:
Since PS is the bisector of ∠QPR
∴∠QPS = ∠RPS = x (say)
In ∆PRT, we have
∠PRT + ∠PTR + ∠RPT = 180°
⇒ ∠PRT + 90° + ∠RPT = 180°
⇒ ∠PRT + ∠RPS + ∠TPS = 90°
⇒ ∠PRT + x + ∠TPS = 90°
⇒ ∠PRT or ∠R = 90° – ∠TPS – x
In ΔΡQT, we have
∠PQT + ∠PTQ + ∠QPT = 180°
⇒ ∠PQT + 90° + ∠QPT = 180°
⇒ ∠PQT + ∠QPS – TPS = 90°
⇒ ∠PQT + x – ∠TPS = 90° [∵∠QPS = x]
⇒ ∠PQT or ∠Q = 90° + ∠TPS – x …(ii)
Subtracting (i) from (ii), we have
⇒ ∠Q – ∠R = (90° + ∠TPS – x) – 190° – ∠TPS – x)
⇒ ∠Q – ∠R = 90° + ∠TPS – X – 90° + ∠TPS + x
⇒ 2∠TPS = 2Q- ∠R
⇒ ∠TPS = \(\frac{1}{2}\)(Q – ∠R)
Lines and Angles Class 9 Extra Questions HOTS
Question 1.
In the given figure, p ll q, find the value of x.
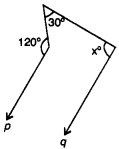
Solution:
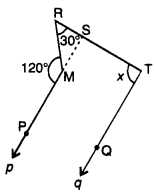
Extend line p to meet RT at S.
Such that MS || QT
Now, in ARMS, we have
∠RMS = 180° – ∠PMR (linear pair]
= 180° – 120°
= 60°
∠RMS + ∠MSR + ∠SRM = 180° [by angle sum property of a ∆]
⇒ 60° + ∠MSR + 30o = 180°
⇒ MSR = 90°
Now, PS || QT – ∠MSR = ∠RTQ
⇒ ∠RTQ = x = MSR = 90° (corresponding ∠s]
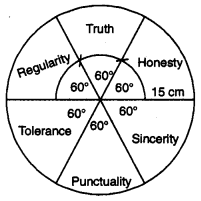
Question 2.
In a triangle, if ∠A = 2∠B = 6∠C, find the measures of ∠A, ∠B and ∠C and find the value of \(\frac{\angle A+2 \angle B}{3 \angle C}\).
Solution:
Let us consider ∠A = 2∠B = 6∠C = x
∴∠A = x
2∠B = x = ∠B = \(\frac{1}{2}\)
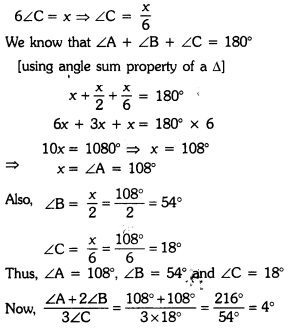
Lines and Angles Class 9 Extra Questions Value Based (VBQs)
Question 1.
Students in a school are preparing banner for a rally to make people aware for saving electricity. What value are they exhibiting by doing so ? Parallel lines I and m are cut by transversal t, if ∠4 = ∠5 and ∠6 = ∠7, what is measure of angle 8 ?
Solution:
Here, given that ∠4 = ∠5 and ∠6 = ∠7
Now, I || m and t is a transversal
∴ ∠4 + ∠5 + ∠6 + ∠7 = 180° [∵ co-interior angles are supplementary]
∠5 + ∠5 + ∠6 + ∠6 = 180° [using (i)]
2(∠5 + ∠6) = 180°
∠5 + ∠6 = 90°
We know that, sum of all interior angles of a triangle is 180°
∴ ∠8 + ∠5 + ∠6 = 180°
⇒ ∠8 + 90° = 180° [using (ii)]
⇒ ∠8 = 180° – 90° = 90°
Save electricity, save energy.
Question 2.
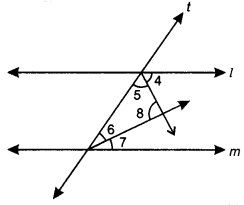
To protect poor people from cold weather, Ram Lal. has given his land to make a shelter home for them. What value is being exhibited by him? In the given figure, ‘sides QP and RQ of ∆PQR are produced to point S and T respectively. If ∠PQT = 110° and ∠SPR = 135°, find ∠PRQ.
Solution:
Here,
∠SPR + ∠QPR = 180° [a linear pair]
135° + ∠QPR = 180° [∵ ∠SPR = 135°]∠
⇒ ∠QPR = 180° – 135° = 45°
In ∆PQR, by exterior angle property, we have
∠QPR + ∠PRQ = ∠PQT
45° + ∠PRQ = 110°
∠PRQ = 110° – 45° = 65°
Helpful nature, service of mankind and helping the needy people.
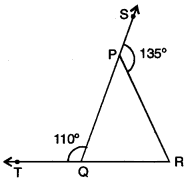
Question 3.
In an activity of mathematics, a teacher ask students to divide a circular sheet of radius 15 cm into 6 equal parts to write 6 values they like. What is the central angle subtended by each part ? Give the six values of your preference.
Solution:
Draw a circle of radius 15 cm and divide the circular region into six equal parts by constructing an angle of measure 60° at the centre.
Central angle subtended by each part
= \(\frac{360^{\circ}}{6}\) = 60°
The six values are : Honesty, Truth, Regularity, Tolerance, Punctuality and Sincerity.