Class 6 Maths Chapter 7 Fractions Notes
Class 6 Maths Chapter 7 Notes – Class 6 Fractions Notes
Fractional Units and Equal Shares
When one unit is divided into several equal parts, each part is called a fractional unit.
e.g. \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots . ., \frac{1}{100}\), etc.
We sometimes refer to fractional units as ‘unit fractions’.
Example 1.
A chocolate bar weighs 1 kg. If it is divided into 8 equal pieces, what is the weight of each piece?
Solution:
Weight of each piece = 1 kg
∵ It is divided into 8 equal pieces.
∴ Weight of each piece = \(\frac{1}{8}\) kg.
Example 2.
A 5-litre big bottle is used to fill 10 smaller bottles equally. How much water does each smaller bottle hold?
Solution:
Amount of water in a big bottle = 5 liters
∴ Amount of water in each smaller bottle = \(\frac{5}{10}\) litres
Each smaller bottle holds \(\frac{1}{2}\) liters of water.
![]()
Fractional Units as Parts of a Whole
A fraction is a number representing part of a whole. The whole may be a single object or a group of objects. It is defined as
Fraction = \(\frac{\text { Numerator }}{\text { Denominator }}=\frac{a}{b}\)
Here, the denominator can never be zero.
e.g. (i) \(\frac{1}{5}\) is a fraction and it is read as one-fifth, which means that 1 part out of 5 equal parts in which the whole is divided. Also, here 1 is called, the numerator, and 5 is called, the denominator.
(ii) If we take a pizza and divide it equally among 4 persons, then each person will have \(\frac{1}{4}\) or written in word, one-quarter of the pizza.
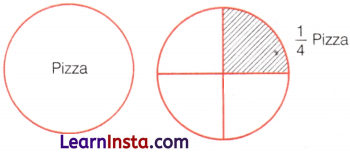
Example 3.
What fraction of a day is 15 hours?
Solution:
We know that, one day = 24 h
∴ The required fraction = \(\frac{15}{24}\)
Example 4.
Write the fraction representing the shaded portion.
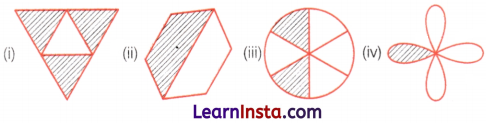
Solution:
(i) Total number of equal parts = 4 and shaded parts = 3
∴ Fraction representing the shaded portion = \(\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{3}{4}\)
(ii) Total number of equal parts = 2 and shaded part = 1
∴ Fraction representing the shaded portion = \(\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{1}{2}\)
(iii) Total number of equal parts = 6 and shaded parts = 2
∴ Fraction representing the shaded portion = \(\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{2}{6}\)
(iv) Total number of equal parts = 4 and shaded part = 1
∴ Fraction representing the shaded portion = \(\frac{\text { Number of shaded parts }}{\text { Total number of equal parts }}=\frac{1}{4}\)
Example 5.
Shade the part according to the given fraction.
Solution:
The figures are shaded as per given fraction shown below.
Example 6.
Identify the error, if any.
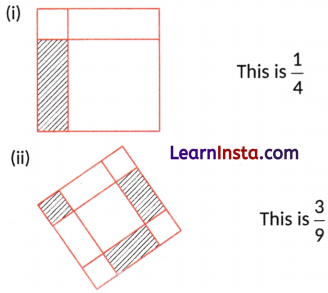
Solution:
(i) In this given figure, four parts are not equal.
So, the fraction is not equal to \(\frac{1}{4}\).
(ii) In this given figure, all the nine parts are not equal.
∴ Fraction is not equal to \(\frac{3}{9}\).
![]()
Example 7.
What fraction of these boxes have cross (✗) in them?

Solution:
Total number of boxes = 8
Number of boxes having cross sign (✗) = 3
∴ Required fraction = \(\frac{\text { Number of boxes having cross } {sign}(\mathbf{x})}{\text { Total number of boxes }}=\frac{3}{8}\)
Example 8.
Write the natural numbers from 113 to 125. What fraction of them are prime numbers?
Solution:
Natural numbers from 113 to 125 = 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125.
Total natural numbers = 13
The prime number from 113 to 125 = 113
Total prime numbers = 1
∴ Required fraction = \(\frac{\text { Total prime numbers }}{\text { Total natural numbers }}=\frac{1}{13}\)
Example 9.
Three girls Manisha, Sakshi, and Shubhangini shared lunch at school. Manisha has brought two burgers, one is a veg burger and one is a non-veg. The other two girls forget to bring their lunch. Manisha agreed to share her burgers so that each person would have an equal share of each burger.
(i) How can Manisha divide her burgers so that each person has an equal share?
(ii) What part of a burger will every girl receive?
Solution:
Total number of burgers = 2
Total number of girls = 3
(i) Here, Manisha has to divide 2 burgers into three people.
So, she will divide each burger into three equal parts and give one part of each burger to each of them.
Thus, each person will get \(\frac{2}{3}\) burgers.
(ii) One burger is to be divided among three girls.
Total number of parts = 6
Each gets 2 parts out of 6. Then, the fraction = \(\frac{2}{6}\)
∴ Each girl will get = \(\frac{1}{3}\) part of a burger.
Example Problems
Question 1.
What fraction of
(i) an hour is 10 min
(ii) an hour is 20 min
(iii) a day is 16 h
Answer:
(i) \(\frac{1}{6}\)
(ii) \(\frac{1}{3}\)
(iii) \(\frac{2}{3}\)
Question 2.
Write the fraction representing the shaded portion.

Answer:
(i) \(\frac{2}{4}\)
(ii) \(\frac{3}{4}\)
(iii) \(\frac{2}{6}\)
(iv) \(\frac{3}{7}\)
Question 3.
What fraction represents the unshaded portion?

Answer:
(i) \(\frac{3}{4}\)
(ii) \(\frac{3}{4}\)
(iii) \(\frac{3}{5}\)
(iv) \(\frac{2}{4}\)
(v) \(\frac{2}{8}\)
Question 4.
Shade the part according to the given fraction.

Answer:

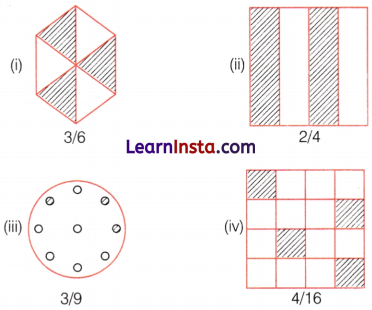
Question 5.
Identify the error if any.

Answer:
(i) not equal to \(\frac{1}{4}\)
(ii) not equal to \(\frac{2}{5}\)
![]()
Question 6.
What fraction of these figures does not have a cross sign (✗) in them?
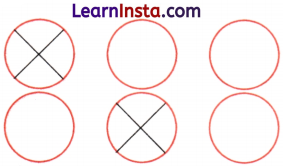
Answer:
\(\frac{4}{6}\)
Question 7.
Write the natural number from 1 to 11. What fraction of them are prime numbers?
Answer:
\(\frac{5}{11}\)
Question 8.
If 11 out of 15 white balls are coloured red, then what fraction of balls are colored white?
Answer:
\(\frac{4}{15}\)
Question 9.
Shubhangini has to read 25 books. She has so far finished reading 10 books. What fraction of the books she has finished reading?
Answer:
\(\frac{10}{25}\)
Question 10.
Megha has ₹ 10, out of which she decided to lend ₹ 7 to her friend. Write the fraction to denote the amount left with her.
Answer:
\(\frac{3}{10}\)
Question 11.
If Aarav has to divide 3 pieces of bread among 5 of his friends so that each person has an equal share of each piece of bread.
(i) How can he divide his breads so that each person has an equal share?
(ii) What part of the bread will each boy receive?
Answer:
(i) \(\frac{3}{5}\)
(ii) \(\frac{1}{5}\)
Measuring, Representation on Number Line and Types of Fractions
Measuring Using Fractional Units
Fraction quantities can be measured using fractional units.
e.g. Let a strip of paper be folded into 4 equal parts as shown below.

Example 1.
Look at the figure given below and measure them using fractional units.

Solution:
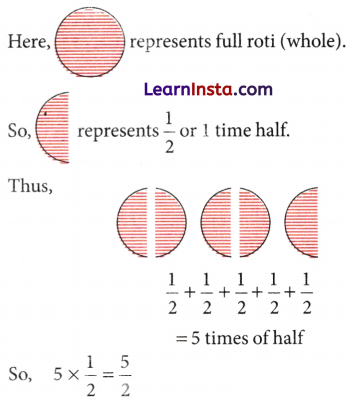
Here, we can that say given figure shows five times half of the roti.
Fraction on the Number Line
Every fraction has a point associated with it on the number line. For this, we will need to divide the gap of 0 to 1 into as many equal parts as in the denominator of that fraction.
Suppose, we want to denote the fraction \(\frac{5}{7}\) on the number line. Now, take a line OP of unit length.

Divide line OP into seven equal parts and take 5 parts out of it to reach point A. Then, the point A represents the fraction \(\frac{5}{7}\).
Example 2.
Show \(\frac{4}{5}\) on a number line.
Solution:
We know that \(\frac{4}{5}\) is greater than zero but less than 1. So, it will lie between 0 and 1.
Now, we have to show \(\frac{4}{5}\) on a number line.
So, we have to divide the length between 0 and 1 into 5 equal parts and take 4 parts out of it to reach point A.

Then, the point A represents the fraction \(\frac{4}{5}\).
![]()
Example 3.
Write the fraction denoted by point A.

Solution:
Point A is marked at fifth place out of 10.
Therefore, the fraction is \(\frac{5}{10}\).
Example 4.
Show \(\frac{2}{9}, \frac{5}{9}, \frac{0}{9}\) and \(\frac{9}{9}\) on a number line.
Solution:
We know that all given fractions are greater than or equal to zero but less than or equal to 1.
So, we have to divide the gap between 0 and 1 into nine equal parts, then each part shows \(\frac{1}{9}\) and 2 part shows \(\frac{2}{9}\), 5 part shows \(\frac{5}{9}\), 9 part shows \(\frac{9}{9}\). Also, 0 shows \(\frac{0}{9}\).

Hence, points A, B, C, and D respectively represent the fraction \(\frac{0}{9}, \frac{2}{9}, \frac{5}{9}\) and \(\frac{9}{9}\).
Example 5.
Write five fractions between 0 and 1 that you can show and depict them on the number line.
Solution:
As we know, we can show many fractions which are greater than 0 and less than 1.
i.e. between 0 and 1.
Five fractions are \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}\) and \(\frac{5}{6}\).
These fractions are shown on a number line as given below.

Hence, points A, B, C, D, and E represent the fractions \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}\) and \(\frac{5}{6}\), respectively.
Between two whole numbers, there lie infinite fractions.
Types of Fraction
Proper Fraction
A fraction whose numerator is always less than the denominator is called a proper fraction.
i.e. Numerator < Denominator.
e.g. \(\frac{9}{10}, \frac{5}{8}\) are proper fractions. It is always less than 1.
So, if we represent a proper fraction on a number line, it will always lie to the left of 1.
Example 6.
Choose the proper fraction from the following numbers. \(6 \frac{1}{2}, \frac{8}{3}, \frac{2}{9}, 7 \frac{2}{3}\)
Solution:
A fraction is a proper fraction if the numerator is less than the denominator.
Therefore, \(\frac{2}{9}\) is a proper fraction.
Example 7.
Give a proper fraction:
(i) Whose numerator is 4 and denominator is 7.
(ii) Whose denominator is 8 and numerator is 1.
(iii) Whose numerator and denominator add upto 8.
How many fractions of this kind can you make?
(iv) Whose denominator is 3 more than numerator.
(Give any five. How many more can you make?)
Solution:
(i) Numerator = 4 and denominator = 7
∴ Required fraction = \(\frac{4}{7}\)
(ii) Numerator = 1 and denominator = 8
∴ Required fraction = \(\frac{1}{8}\)
(iii) Possible pairs of numerator and denominator which add upto 8 are (0, 8), (1, 7), (2, 6), (3, 5).
Now, proper fractions = \(\frac{0}{8}, \frac{1}{7}, \frac{2}{6}, \frac{3}{5}\)
There are four fractions. So, we can make four such fractions.
(iv) There can be an infinite number of fractions whose denominator is 3 more than the numerator.
Some of them \(\frac{0}{3}, \frac{1}{4}, \frac{2}{5}, \frac{3}{6}, \frac{4}{7}\),…… so on.
Example 8.
Fill up using one of these: ‘>’, ‘<‘ or ‘=’
(i) \(\frac{1}{4}\) ____ 1
(ii) 1 ____ \(\frac{2}{5}\)
(iii) \(\frac{6}{6}\) ____ 1
(iv) \(\frac{2023}{2023}\) ____ 1
Solution:
(i) \(\frac{1}{4}\) < 1 (ii) 1 > \(\frac{2}{5}\)
(iii) \(\frac{6}{6}\) = 1
(iv) \(\frac{2023}{2023}\) = 1
Improper Fraction
A fraction whose numerator is always greater than the denominator is called an improper fraction.
i.e. Numerator > Denominator.
e.g. \(\frac{3}{2}, \frac{18}{5}\) are improper fractions.
It is always greater than 1. So, if we represent an improper fraction on a number line, it will always lie to the right of 1.
Example 9.
Write five improper fractions with denominator 8.
Solution:
Five improper fractions with denominator 8 are \(\frac{9}{8}, \frac{10}{8}, \frac{11}{8}, \frac{12}{8}, \frac{13}{8}\).
Mixed Fraction
A fraction which is a combination of a whole number and a proper fraction (or part) is called a mixed fraction.
e.g. 1\(\frac{1}{4}\) is a mixed fraction.
Here, 1 is a whole number and \(\frac{1}{4}\) is a proper fraction.
![]()
Example 10.
Combine the following as a mixed fraction.
(i) 2 and one-third
(ii) 5 and \(\frac{3}{5}\)
Solution:
(i) We have, 2 and one-third.
Here, whole part = 2 and proper fraction part = One-third = \(\frac{1}{3}\)
∴ Mixed fraction = 2\(\frac{1}{3}\)
(ii) We have, 5 and \(\frac{3}{5}\).
Here, whole part = 5 and proper fraction = \(\frac{3}{5}\)
∴ Mixed fraction = 5\(\frac{3}{5}\)
Conversion of an Improper Fraction into a Mixed Fraction
To express an improper fraction as a mixed fraction, firstly we divide the numerator by the denominator to obtain the quotient and the remainder. Then,
Mixed fraction = \(\text { Quotient } \frac{\text { Remainder }}{\text { Divisor }}\)
e.g. Consider an improper fraction = \(\frac{17}{4}\)
Now, by dividing the numerator by the denominator i.e. 17 by 4, we get
quotient = 4 and remainder = 1
Hence, mixed fraction = 4\(\frac{1}{4}\)
Example 11.
Express the following as mixed fractions.
(i) \(\frac{19}{3}\)
(ii) \(\frac{14}{4}\)
(iii) \(\frac{17}{7}\)
(iv) \(\frac{33}{9}\)
Solution:
(i) we have, \(\frac{19}{3}\)

On dividing 19 by 3, we get quotient = 6 and remainder = 1.
Hence, mixed fraction = 6\(\frac{1}{3}\)
(ii) We have, \(\frac{14}{4}\)

On dividing 14 by 4, we get quotient = 3 and remainder = 2
Hence, mixed fraction = 3\(\frac{2}{4}\)
(iii) We have, \(\frac{17}{7}\)

On dividing 17 by 7, we get quotient = 2 and remainder = 3
Hence, mixed fraction = 2\(\frac{3}{7}\)
(iv) we have, \(\frac{33}{9}\)

On dividing 33 by 9, we get quotient = 3 and remainder = 6
Hence, mixed fraction = 3\(\frac{6}{9}\)
Conversion of a Mixed Fraction into an Improper Fraction
Multiply the whole number with the denominator of the fraction and then add the numerator of the fraction. This gives the numerator of the required improper fraction. Its denominator is the same as the denominator of the fractional part of a mixed fraction.
Improper fraction \(=\frac{\text { Whole Number } \times \text { Denominator }+ \text { Numerator }}{\text { Denominator }}\)
Example 12.
Express the following fractions as improper fractions.
(i) 3\(\frac{2}{5}\)
(ii) 2\(\frac{3}{7}\)
(iii) 7\(\frac{1}{4}\)
(iv) 3\(\frac{1}{6}\)
(v) 7\(\frac{3}{8}\)
(vi) 11\(\frac{3}{2}\)
Solution:

Example Problems
Question 1.
Continue the table (given below) of \(\frac{1}{2}\) for 2 more steps. (![]() represents a whole)
represents a whole)

Answer:

Question 2.
Show \(\frac{7}{11}\) on a number line.
Answer:
Do it yourself.
Question 3.
Write the fraction denoted by point A.
![]()
Answer:
\(\frac{4}{9}\)
Question 4.
Can you show any fraction between 1 and 2? Write five fractions that you can show and depict them on a number line.
Answer:
Yes, \(\frac{7}{6}, \frac{8}{6}, \frac{9}{6}, \frac{10}{6}, \frac{11}{6}\)
![]()
Question 5.
Choose the proper function from the following.
\(7 \frac{1}{2}, \frac{7}{4}, \frac{4}{9}, 8 \frac{1}{3}\)
Answer:
\(\frac{4}{9}\)
Question 6.
Give a proper fraction
(i) Whose numerator is 7 and denominator is 15.
(ii) Whose denominator is 11 and numerator is 2.
(iii) Whose numerator and denominator add upto 6.
(iv) Whose denominator is 2 more than the numerator.
Answer:
(i) \(\frac{7}{15}\)
(ii) \(\frac{2}{11}\)
(iii) \(\frac{1}{5}\), \(\frac{2}{4}\)
(iv) \(\frac{1}{3}, \frac{2}{4}, \frac{3}{5}, \frac{4}{6}\) and so on
Question 7.
Fill up using one of these: > or < or =.
(i) \(\frac{1}{3}\) _____ 1
(ii) \(\frac{3}{7}\) _____ 1
(iii) 1 ______ \(\frac{6}{11}\)
(iv) \(\frac{9}{9}\) ______ 1
Answer:
(i) \(\frac{1}{3}\) < 1
(ii) \(\frac{3}{7}\) < 1 (iii) 1 > \(\frac{6}{11}\)
(iv) \(\frac{9}{9}\) = 1
Question 8.
Combine the following as a mixed fraction.
(i) 7 and \(\frac{1}{9}\)
(ii) 6 and \(\frac{2}{3}\)
Answer:
(i) 7\(\frac{1}{9}\)
(ii) 6\(\frac{2}{3}\)
Question 9.
Express the following as a mixed fraction.
(i) \(\frac{20}{7}\)
(ii) \(\frac{35}{8}\)
(iii) \(\frac{113}{7}\)
Answer:
(i) 2\(\frac{6}{7}\)
(ii) 4\(\frac{3}{8}\)
(iii) 16\(\frac{1}{7}\)
Question 10.
Express the following as an improper fraction.
(i) 2\(\frac{5}{9}\)
(ii) 5\(\frac{3}{7}\)
(iii) 16\(\frac{1}{7}\)
Answer:
(i) \(\frac{23}{9}\)
(ii) \(\frac{38}{7}\)
(iii) \(\frac{113}{7}\)
Equivalent Fraction and Simplest Form of a Fraction
Equivalent Fraction
Fractions having the same values are called equivalent fractions.
To find an equivalent fraction of a given number, we multiply or divide the numerator and the denominator of the given fraction by the same non-zero number.
Example 1.
Find five equivalent fractions of each of the following.
(i) \(\frac{2}{3}\)
(ii) \(\frac{1}{5}\)
Solution:

Example 2.
Give an example of four equivalent fractions.
Solution:
Four equivalent fractions are \(\frac{1}{3}, \frac{2}{6}, \frac{3}{9}, \frac{4}{12}\), etc.
To Test Whether Two Given Fractions are Equivalent or not
We can check whether two fractions are equivalent or not by finding their cross product i.e. we multiply the numerator of the first fraction with the denominator of the second fraction and the denominator of the first fraction with the numerator of the second fraction. If the two products are equal, then the given fractions are equivalent, they are not.
Let \(\frac{a}{b}\) and \(\frac{c}{d}\) be two given fractions.
Their cross-multiplication shown as ![]()
(i) If ad = bc, then \(\frac{a}{b}\) and \(\frac{c}{d}\) are equivalent.
(ii) If ad < bc, then \(\frac{a}{b}<\frac{c}{d}\) (iii) If ad > bc, then \(\frac{a}{b}>\frac{c}{d}\)
![]()
Example 3.
Check whether the fractions \(\frac{5}{8}\) and \(\frac{15}{24}\) are equivalent or not.
Solution:

Example 4.
Identify the fractions in each. Are these fractions equivalent?

Solution:
(i) Here, the total number of parts are 4, out of which 2 parts are shaded.
So, required fraction = \(\frac{2}{4}\)
(ii) Here, the total parts are 6, out of which 3 parts are shaded.
So, required fraction = \(\frac{3}{6}\)
Now, take \(\frac{2}{4}\) and \(\frac{3}{6}\).
Here, 2 × 6 = 12 and 3 × 4 = 12
∵ 12 = 12
∴ \(\frac{2}{4}\) and \(\frac{3}{6}\) are equivalent.
Example 5.
Write a fraction equivalent to \(\frac{3}{5}\) with numerator 12.
Solution:
Let D stands for the denominator.
Given, the numerator of an equivalent fraction = 12
\(\frac{12}{D}=\frac{3}{5}\)
⇒ D × 3 = 12 × 5
⇒ D = \(\frac{12 \times 5}{3}\) = 20
Hence, required equivalent fraction of \(\frac{3}{5}\) is \(\frac{12}{20}\).
Example 6.
Write a fraction equivalent to \(\frac{5}{7}\) with denominator 35.
Solution:
Let N stands for the numerator.
Given, the denominator of an equivalent fraction = 35
\(\frac{N}{35}=\frac{5}{7}\)
⇒ N × 7 = 35 × 5
⇒ N = \(\frac{35 \times 5}{7}\) = 25
Hence, required equivalent fraction of \(\frac{5}{7}\) is \(\frac{25}{35}\).
Simplest Form of a Fraction
A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1 i.e. their HCF = 1.
In other words, a fraction is said to be in the lowest term if its numerator and denominator are as small as possible.
To find the equivalent fraction in the simplest form, firstly we find the HCF of the numerator and denominator and then divide both of them by their HCF.
Example 7.
Write the simplest form of
(i) \(\frac{28}{42}\)
(ii) \(\frac{36}{49}\)
Solution:
(i) We have, \(\frac{28}{42}\)
Now, factors of 28 = 2, 2, 7 and factors of 42 = 2, 3, 7
Common factors = 2 and 7
∴ HCF of 28 and 42 = 2 × 7 = 14
Then \(\frac{28}{42}=\frac{28 \div 14}{42 \div 14}=\frac{2}{3}\)
Hence, fraction \(\frac{2}{3}\) is the simplest form of a given fraction.
(ii) Here, factors of 36 = 6, 6 and factors of 49 = 7, 7
∴ 36 and 49 have no common factor except 1.
Hence, fraction \(\frac{36}{49}\) is in simplest form.
Example Problems
Question 1.
Write four equivalent fractions of each of the following.
(i) \(\frac{3}{7}\)
(ii) \(\frac{5}{11}\)
Answer:
(i) \(\frac{6}{14}, \frac{9}{21}, \frac{12}{28}, \frac{15}{35}\)
(ii) \(\frac{10}{22}, \frac{15}{33}, \frac{20}{44}, \frac{25}{55}\)
Question 2.
Give an example of four equivalent fractions.
Answer:
Do it yourself.
Question 3.
State whether \(\frac{12}{15}\) is an equivalent fraction of \(\frac{2}{5}\).
Answer:
No
Question 4.
Which of the following represents equivalent fractions?

Answer:
(ii) and (iii)
Question 5.
Write a fraction equivalent to \(\frac{36}{63}\) with numerator 4.
Answer:
\(\frac{4}{7}\)
Question 6.
Write a fraction equivalent to \(\frac{5}{8}\) with denominator 56.
Answer:
\(\frac{35}{56}\)
Question 7.
Write the simplest form of the following.
(i) \(\frac{91}{26}\)
(ii) \(\frac{7}{9}\)
(iii) \(\frac{169}{196}\)
Answer:
(i) \(\frac{7}{2}\)
(ii) \(\frac{7}{9}\)
(iii) \(\frac{169}{196}\)
Like, Unlike, and Comparing Fractions
Like and Unlike Fractions
Fractions having the same denominator are called fractions.
e.g. \(\frac{1}{7}, \frac{2}{7}, \frac{3}{7}\), etc.
While fractions having different denominators are called unlike fractions.
e.g. \(\frac{2}{3}, \frac{1}{5}, \frac{2}{15}, \frac{7}{9}\), etc.
Conversion of Unlike Fraction into Like Fraction
Unlike fractions are converted into like fractions by converting each of them into their equivalent fractions having a denominator equal to the LCM of all the denominators of all unlike fractions.
Example 1.
Convert the fractions \(\frac{1}{2}\), \(\frac{2}{3}\) and \(\frac{5}{6}\) into like fractions.
Solution:
The given fractions are \(\frac{1}{2}\), \(\frac{2}{3}\) and \(\frac{5}{6}\).
LCM of denominators 2, 3, and 6 = 6
We convert each of the fractions into an equivalent fraction with 6 as the denominator.


The required like fractions are \(\frac{3}{6}\), \(\frac{4}{6}\) and \(\frac{5}{6}\).
Comparing Fractions
There are two methods of comparison of fractions which are given below:
Comparison of Like Fractions
If two fractions have the same denominator, then the fraction with the greater numerator is greater.
e.g. Between \(\frac{11}{20}\) and \(\frac{13}{20}\), the traction \(\frac{13}{20}\) is greater.
![]()
Example 2.
Which is the larger fraction?
(i) \(\frac{6}{10}\) or \(\frac{7}{10}\)
(ii) \(\frac{12}{24}\) or \(\frac{13}{24}\)
Solution:
(i) We have, \(\frac{6}{10}\) or \(\frac{7}{10}\)
Here, denominators of both fractions are the same, and 7 > 6.
so, \(\frac{7}{10}>\frac{6}{10}\)
(ii) We have, \(\frac{12}{24}\) or \(\frac{13}{24}\).
Here, denominators of both fractions are the same, and 13 > 12.
So, \(\frac{13}{24}>\frac{12}{24}\)
Example 3.
Parul reads 20 pages of a novel containing 100 pages. Sachin reads \(\frac{2}{5}\) of the same book. Who reads less?
Solution:
Fraction of book read by Parul = \(\frac{20}{100}\) = \(\frac{1}{5}\)
Fraction of novel read by Sachin = \(\frac{2}{5}\)
Here, the denominator of both fractions are same, and 2 > 1.
∴ \(\frac{1}{5}<\frac{2}{5}\)
Hence, Parul read fewer pages of the novel.
Example 4.
Write the following in ascending and descending order.
(i) \(\frac{2}{9}, \frac{7}{9}, \frac{5}{9}\)
(ii) \(\frac{1}{3}, \frac{11}{3}, \frac{4}{3}, \frac{7}{3}, \frac{5}{3}\)
Solution:
(i) We have, \(\frac{2}{9}, \frac{7}{9}, \frac{5}{9}\)
Here, the denominator of all fractions are same.
∴ Ascending order of numerator = 2 < 5 < 7 and descending order of numerator = 7 > 5 > 2
∴ Ascending order of fraction = \(\frac{2}{9}<\frac{5}{9}<\frac{7}{9}\) and descending order of fraction = \(\frac{7}{9}>\frac{5}{9}>\frac{2}{9}\)
(ii) Since the denominator of all fractions are same.
∴ Ascending order of fraction = \(\frac{1}{3}<\frac{4}{3}<\frac{5}{3}<\frac{7}{3}<\frac{11}{3}\) and descending order of fraction = \(\frac{11}{3}>\frac{7}{3}>\frac{5}{3}>\frac{4}{3}>\frac{1}{3}\)
Example 5.
Write the shaded portion as a fraction. Arrange them in ascending and descending order using the correct sign ‘<‘, ‘>’ between the fractions.

Solution:
Here, the total number of equal parts in all figures = 8
Shaded portion of figure (i) represents fraction = \(\frac{2}{8}\)
Shaded portion of figure (ii) represents fraction = \(\frac{4}{8}\)
Shaded portion of figure (iii) represents fraction = \(\frac{3}{8}\)
Shaded portion of figure (iv) represents fraction = \(\frac{6}{8}\)
∴ The denominator of all fractions is the same. So, we arrange them in ascending and descending order according to their numerators.
∴ Ascending order of fractions = \(\frac{2}{8}<\frac{3}{8}<\frac{4}{8}<\frac{6}{8}\) [∵ fraction with small numerator will be smaller]
and descending order of fractions = \(\frac{6}{8}>\frac{4}{8}>\frac{3}{8}>\frac{2}{8}\)
[∵ fraction having greatest numerator will be greatest].
Comparison of Unlike Fractions
There are two types of comparison of unlike fractions.
Comparison of Unlike Fractions with Same Numerators
Among two fractions with the same numerator, the one with the smaller denominator is the greater.
e.g. \(\frac{7}{11}>\frac{7}{13} \text { and } \frac{11}{23}>\frac{11}{25}\)
Example 6.
Arrange the following in ascending and descending order.
\(\frac{2}{13}, \frac{2}{11}, \frac{2}{17}, \frac{2}{5}, \frac{2}{7}, \frac{2}{9}, \frac{2}{55}\)
Solution:
Here, the numerator of all fractions are same.
Descending order of denominators = 55 > 17 > 13 > 11 > 9 > 7 > 5.
∴ Ascending order of fraction = \(\frac{2}{55}<\frac{2}{17}<\frac{2}{13}<\frac{2}{11}<\frac{2}{9}<\frac{2}{7}<\frac{2}{5}\) [∵ \(\frac{2}{55}\) has larger denominator, so it is the smallest fraction]
and descending order of fractions = \(\frac{2}{5}>\frac{2}{7}>\frac{2}{9}>\frac{2}{11}>\frac{2}{13}>\frac{2}{17}>\frac{2}{55}\)
Example 7.
Kanchan and Kiran are two friends. Kanchan gets one-fifth of a bottle of apple juice and Kiran gets one-fourth of a bottle of apple juice, who gets more?
Solution:
Here, we will compare one-fifth i.e. \(\frac{1}{5}\) and one-fourth i.e. \(\frac{1}{4}\).
Since \(\frac{1}{5}\) and \(\frac{1}{4}\) have the same numerator, the fraction with a smaller denominator is greater.
Thus, \(\frac{1}{4}\) > \(\frac{1}{5}\).
Thus, Kiran gets more apple juice.
Comparison of Unlike Fractions with Different Numerators
If the numerator and denominator both are different of the given two fractions, then for comparing, we use the method of equivalent fractions i.e. we change the denominator of a fraction without changing its value.
Example 8.
Compare \(\frac{5}{6}\) and \(\frac{13}{15}\).
Solution:
The given fractions are unlike, we should first get their equivalent fractions with a denominator, which is a common multiple of 6 and 15 i.e. 30.
Now, \(\frac{5 \times 5}{6 \times 5}=\frac{25}{30}\) and \(\frac{13 \times 2}{15 \times 2}=\frac{26}{30}\)
Since, \(\frac{26}{30}>\frac{25}{30}\), so \(\frac{13}{15}>\frac{5}{6}\)
![]()
Example 9.
Arrange the following in ascending and descending order.
\(\frac{2}{3}, \frac{1}{9}, \frac{5}{12}\) and \(\frac{7}{36}\)
Solution:
We have, \(\frac{2}{3}, \frac{1}{9}, \frac{5}{12}, \frac{7}{36}\)
LCM of 3, 9, 12 and 36 = 3 × 3 × 4 = 36
So, we convert each of the given fractions into an equivalent fraction with denominator 36.


Example 10.
Compare and put appropriate signs between the given fractions.
(i) \(\frac{3}{5}\) ______ \(\frac{4}{5}\)
(ii) \(\frac{2}{5}\) ______ \(\frac{2}{7}\)
Solution:
(i) We have, \(\frac{3}{5}\) ______ \(\frac{4}{5}\)
Here, denominators are the same for both fractions.
So, fractions having smaller numerators will be smaller.
∴ \(\frac{3}{5}\) < \(\frac{4}{5}\)
(ii) We have, \(\frac{2}{5}\) ______ \(\frac{2}{7}\)
Here, numerators are the same for both fractions.
So, a fraction having a smaller denominator will be greater.
∴ \(\frac{2}{5}\) > \(\frac{2}{7}\)
Example 11.
Find the answer to the following. Write and indicate how you solved them.
(i) Is \(\frac{5}{4}\) equal to \(\frac{9}{5}\)?
(ii) Is \(\frac{20}{16}\) equal to \(\frac{5}{4}\)?
Solution:
(i) LCM of 4 and 5 = 20
Now, \(\frac{5}{4}=\frac{5 \times 5}{4 \times 5}=\frac{25}{20}\)
and \(\frac{9}{5}=\frac{9 \times 4}{5 \times 4}=\frac{36}{20}\)
Thus, both fractions are like fractions but \(\frac{25}{20} \neq \frac{36}{20}\)
∴ \(\frac{5}{4} \neq \frac{9}{5}\)
(ii) LCM of 16 and 4 = 16
Now, \(\frac{20}{16}=\frac{20 \times 1}{16 \times 1}=\frac{20}{16}\)
and \(\frac{5}{4}=\frac{5 \times 4}{4 \times 4}=\frac{20}{16}\)
Thus, both fractions are like fractions and \(\frac{20}{16}\) = \(\frac{20}{16}\)
∴ \(\frac{20}{16}\) = \(\frac{5}{4}\)
Example 12.
Ravish takes 2\(\frac{1}{5}\) min to walk across the school ground. Rahul takes 1\(\frac{3}{4}\) min to do the same. Who takes less time and by what fraction?
Solution:
Time taken by Ravish to walk across the school ground = 2\(\frac{1}{5}\) min = \(\frac{11}{5}\) min
Time taken by Rahul to walk across the school ground = 1\(\frac{3}{4}\) min = \(\frac{7}{4}\) min
The LCM of 5 and 4 = 20
∴ \(\frac{11}{5}=\frac{11 \times 4}{5 \times 4}=\frac{44}{20}\) and \(\frac{7}{4}=\frac{7 \times 5}{4 \times 5}=\frac{35}{20}\)
Now, \(\frac{35}{20}\) < \(\frac{44}{20}\)
∴ \(\frac{7}{4}\) < \(\frac{11}{5}\)
∴ Rahul takes less time.
The difference between the time taken by Ravish and Rahul to walk across the school ground = \(\frac{11}{5}-\frac{7}{4}\) = \(\frac{9}{20}\) min
Thus, Rahul takes \(\frac{9}{20}\) min less than Ravish.
Example 13.
Asha and Deepa have bookshelves of the same size partly filled with books. Asha’s shelf is \(\frac{5}{7}\)th full and Deepa’s shelf is \(\frac{3}{5}\)th full. Whose bookshelf is full? By what fraction?
Solution:
Here, we have to compare two, unlike fractions.
Asha’s shelf = \(\frac{5}{7}\)th
Deepa’s shelf = \(\frac{3}{5}\)th
∴ LCM of 7 and 5 = 35
∴ \(\frac{5}{7}=\frac{5 \times 5}{7 \times 5}=\frac{25}{35}\) and \(\frac{3}{5}=\frac{3 \times 7}{5 \times 7}=\frac{21}{35}\)
∵ 25 > 21
∴ \(\frac{5}{7}>\frac{3}{5}\)
Hence, Asha’s bookshelf is filled more than Deepa’s bookshelf.
∴ Difference = \(\frac{5}{7}-\frac{3}{5}=\frac{25}{35}-\frac{21}{35}=\frac{4}{35}\)
Therefore, Asha’s bookshelf is more full by \(\frac{4}{35}\) than Deepa’s bookshelf.
Example Problems
Question 1.
Convert the following into like fractions \(\frac{4}{7}, \frac{5}{9}, \frac{2}{3}\).
Answer:
\(\frac{36}{63}, \frac{35}{63}, \frac{42}{63}\)
Question 2.
Which is the larger fraction.
(i) \(\frac{3}{5}\) or \(\frac{7}{5}\)
(ii) \(\frac{6}{24}\) or \(\frac{13}{24}\)
Answer:
(i) \(\frac{7}{5}\)
(ii) \(\frac{13}{24}\)
Question 3.
Apurva reads 15 pages of a novel containing 35 pages. Sachin reads \(\frac{2}{7}\) of the same book. Who reads less?
Answer:
Sachin reads fewer pages of the novel.
Question 4.
Write the following in ascending and descending order.
(i) \(\frac{3}{7}, \frac{4}{7}, \frac{6}{7}\)
(ii) \(\frac{7}{11}, \frac{1}{11}, \frac{2}{11}, \frac{12}{11}\)
Answer:
(i) Descending order: \(\frac{6}{7}>\frac{4}{7}>\frac{3}{7}\)
and ascending order: \(\frac{3}{7}<\frac{4}{7}<\frac{6}{7}\)
(ii) Descending order: \(\frac{12}{11}>\frac{7}{11}>\frac{2}{11}>\frac{1}{11}\)
and ascending order: \(\frac{1}{11}<\frac{2}{11}<\frac{7}{11}<\frac{12}{11}\)
![]()
Question 5.
Arrange the following in ascending and descending order.
\(\frac{2}{7}, \frac{2}{17}, \frac{2}{9}, \frac{2}{19}, \frac{2}{13}\)
Answer:
Ascending order of fractions = \(\frac{2}{19}<\frac{2}{17}<\frac{2}{13}<\frac{2}{9}<\frac{2}{7}\)
Descending order of fractions = \(\frac{2}{7}>\frac{2}{9}>\frac{2}{13}>\frac{2}{17}>\frac{2}{19}\)
Question 6.
Mehak used \(\frac{3}{6}\) of a chalk. Dimple used \(\frac{1}{3}\) of the chalk. Who used more of the chalk among both of them?
Answer:
Mehak
Question 7.
Compare \(\frac{7}{9}\) and \(\frac{13}{15}\).
Answer:
\(\frac{13}{15}>\frac{7}{9}\)
Question 8.
Arrange the following in ascending and descending order.
\(\frac{5}{9}, \frac{1}{7}, \frac{8}{13}\) and \(\frac{7}{3}\)
Answer:
Ascending order of fractions = \(\frac{1}{7}<\frac{5}{9}<\frac{8}{13}<\frac{7}{3}\) Descending order of fractions = \(\frac{7}{3}>\frac{8}{13}>\frac{5}{9}>\frac{1}{7}\)
Question 9.
Compare the fractions and put the appropriate sign >, < or =.
(i) \(\frac{12}{14}\) ________ \(\frac{7}{9}\)
(ii) \(\frac{4}{7}\) ________ \(\frac{3}{5}\)
(iii) \(\frac{7}{13}\) ________ \(\frac{28}{52}\)
Answer:
(i) \(\frac{12}{14}\) > \(\frac{7}{9}\)
(ii) \(\frac{4}{7}\) < \(\frac{3}{5}\)
(iii) \(\frac{7}{13}\) = \(\frac{28}{52}\)
Question 10.
Which of the following represents the smallest fraction?

Answer:

Question 11.
Find the answer to the following. Write and indicate how you solved them.
(i) Is \(\frac{7}{5}\) equal to \(\frac{9}{7}\)?
(ii) Is \(\frac{25}{17}\) equal to \(\frac{3}{7}\)?
Answer:
(i) No
(ii) No
Question 12.
A triangle is divided into 4 equal parts and 3 out of it are painted red, whereas a square is divided into 8 equal parts, and 7 out of them are painted red. Which of the shaded parts represents a bigger fraction?
Answer:
Painted part of the square
Question 13.
Ritesh cuts a pizza into 12 pieces and distributes 7 out of it to his friends while Jitesh cuts another pizza into 8 pieces and distributes 5 out of it to his friends. Who distributed more part of the pizza to his friends?
Answer:
Jitesh
Addition and Subtraction of Like Fractions
Addition of Like Fractions
To add fractions, we add their numerators keeping the denominator unchanged, and then write it in simplest form.
Suppose, we have two like fractions \(\frac{a}{b}\) and \(\frac{c}{b}\), then sum = \(\frac{a+c}{b}\)
∴ Sum of like fractions = \(\frac{Sum of their numerators}{Common denominator}\)
e.g. By pictorial representation

Example 1.
Add
(i) \(\frac{1}{8}+\frac{1}{8}\)
(ii) \(\frac{2}{5}+\frac{3}{5}\)
Solution:

Example 2.
Add the shaded part of the fraction for the given figure.

Solution:

Example 3.
Add these with the help of a diagram.
(i) \(\frac{2}{6}+\frac{3}{6}\)
(ii) \(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\)
Solution:
(i) Here, draw two rectangles and divide them into 6 equal parts separately.
In a first rectangle, 2 parts out of 6 parts are shaded and in the second rectangle, 3 parts out of 6 parts are shaded.
On adding them, we get

Example 4.
On her birthday Niharika divided a cake into 6 equal parts. She distributed 2 parts in her family and 3 parts in the neighborhood. How much cake did she distribute together?
Solution:
Here, Niharika divided the cake into 6 equal parts, so each part will represent \(\frac{1}{6}\).
She gave two parts in her family, i.e. \(\frac{2}{6}\)
and she gave three parts in the neighborhood, i.e. \(\frac{3}{6}\).
Part of cake she distributed = \(\frac{3}{6}+\frac{2}{6}\)
Here, the denominator of both fractions are same. So, we add a numerator to find their sum.
i.e. \(\frac{3+2}{6}=\frac{5}{6}\)
Hence, she distributed \(\frac{5}{6}\) of the cake to her family and neighborhood.
![]()
Subtraction of Like Fractions
To subtract like fractions, we subtract the smaller numerator from the greater numerator, keeping the denominator unchanged, and then write it in simplest form.
Suppose, we have two like fractions \(\frac{a}{b}\) and \(\frac{c}{b}\) (a > c), then
Difference = \(\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}\)
∴ Difference of like fractions \(=\frac{\text { Difference of their numerators }}{\text { Common denominator }}\)
Example 5.
Find the difference of \(\frac{7}{9}\) and \(\frac{2}{9}\).
Solution:
Let \(\frac{a}{b}=\frac{7}{9}\) and \(\frac{c}{b}=\frac{2}{9}\)
Here, a > c i.e. 7 > 2
So, Difference = \(\frac{\text { Difference of their numerators }}{\text { Common denominator }}=\frac{7-2}{9}=\frac{5}{9}\)
Example 6.
Mohit was reading a book. He read one-third of the book on Sunday. He read another one-third on Wednesday and the remaining on Friday. What fraction of the book did he read on Friday?
Solution:
Book read by Mohit on Sunday = \(\frac{1}{3}\)
Book read by Mohit on Wednesday = \(\frac{1}{3}\)
∴ Book read by him on Friday = \(1-\frac{1}{3}-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}-\frac{1}{3}\) [∵ 1 and \(\frac{3}{3}\) are equivalent fractions]
= \(\frac{3-1-1}{3}\)
= \(\frac{1}{3}\)
Hence, he read one-third of the book on Friday.
Example 7.
Find the missing fractions \(\frac{9}{10}\) – _______ = \(\frac{7}{10}\).
Solution:
We have, \(\frac{9}{10}\) – _______ = \(\frac{7}{10}\)
Here, missing fraction is subtracted from \(\frac{9}{10}\) to get \(\frac{7}{10}\).
This means on adding missing term to \(\frac{7}{10}\), we get \(\frac{9}{10}\).
So, we subtract \(\frac{7}{10}\) from \(\frac{9}{10}\) to get the missing fraction.
∴ Missing fraction = \(\frac{9}{10}-\frac{7}{10}=\frac{9-7}{10}=\frac{2}{10} \text { or } \frac{1}{5}\)
Thus, \(\frac{9}{10}-\frac{2}{10}=\frac{7}{10}\)
Example 8.
Add the difference of \(\frac{7}{10}\) and \(\frac{2}{10}\) to \(\frac{8}{10}\).
Solution:
Difference of \(\frac{7}{10}\) and \(\frac{2}{10}\) is equal to \(\frac{7}{10}\) – \(\frac{2}{10}\).
[since both are like fractions and 7 is greater than 2, so subtract \(\frac{2}{10}\) from \(\frac{7}{10}\)]
Now, \(\frac{7}{10}-\frac{2}{10}=\frac{7-2}{10}=\frac{5}{10} \text { or } \frac{1}{2}\)
Now, adding \(\frac{5}{10}\) to \(\frac{8}{10}\) i.e. \(\frac{5}{10}+\frac{8}{20}\)
Here, LCMs of 10 and 20 are 20.
∴ \(\frac{5 \times 2}{10 \times 2}+\frac{8}{20}=\frac{10}{20}+\frac{8}{20}=\frac{18}{20}=\frac{9}{10}\)
Example Problems
Question 1.
Find the sum of the following.
(i) \(\frac{11}{15}+\frac{12}{15}\)
(ii) \(\frac{13}{19}+\frac{11}{19}\)
Solution:
(i) \(\frac{23}{15}\)
(ii) \(\frac{24}{19}\)
Question 2.
Add the shaded part of the fraction for the given figure.

Solution:
1
![]()
Question 3.
Find the difference between the following.
(i) \(\frac{19}{21}-\frac{15}{21}\)
(ii) \(\frac{39}{51}-\frac{20}{51}\)
Solution:
(i) \(\frac{4}{21}\)
(ii) \(\frac{19}{51}\)
Question 4.
Sunil donated ₹ 700 out of his pocket money of ₹ 1000 whereas Neha donated ₹ 300 out of ₹ 3000. Who distributed more and how much?
Solution:
Sunil by \(\frac{6}{10}\)
Question 5.
Nandini house is 2\(\frac{9}{10}\) km away from her school. She walked some distance and then took a bus for 1\(\frac{1}{4}\) km to reach the school. How far did she walk?
Solution:
1\(\frac{13}{20}\) km
Question 6.
Parul bought 5\(\frac{1}{2}\) L of milk. Out of this milk, 3\(\frac{1}{2}\) L was consumed. How much milk is left with her?
Solution:
2 L
Question 7.
Find the missing fraction.
(i) \(\frac{8}{12}\) – ______ = \(\frac{5}{12}\)
(ii) \(\frac{3}{16}\) – _____ = \(\frac{1}{16}\)
(iii) \(\frac{8}{15}\) + ______ = \(\frac{12}{15}\)
(iv) ____ – \(\frac{2}{27}\) = \(\frac{6}{27}\)
Solution:
(i) \(\frac{3}{12}\)
(ii) \(\frac{2}{16}\)
(iii) \(\frac{4}{15}\)
(iv) \(\frac{8}{27}\)
Question 8.
Add the difference of \(\frac{7}{12}\) and \(\frac{5}{12}\) to \(\frac{10}{24}\).
Solution:
\(\frac{7}{12}\)
Brahmagupta’s Method for Adding Fractions and for Subtracting Fractions
Addition of Unlike Fractions
To add unlike fractions, we first convert them into equivalent fractions with the same denominator (which is LCM of denominators) and then add them as like fractions.
Example 1.
Add the following.
(i) \(\frac{2}{6}\) and \(\frac{3}{4}\)
(ii) \(\frac{3}{7}\) and \(\frac{5}{8}\)
Solution:

Example 2.
Karishma bought \(\frac{3}{5}\) m of cloth for her college dress and her mother bought \(\frac{2}{7}\) m of cloth. What is the total length of the cloth they bought?
Solution:
Given, cloth bought by Karishma = \(\frac{3}{5}\) m
and cloth bought by her mother = \(\frac{2}{7}\) m
∴ Total length of cloth bought by them = \(\left(\frac{3}{5}+\frac{2}{7}\right)\) m
Now, LCM of 5 and 7 = 35
∴ \(\frac{3}{5}+\frac{2}{7}=\frac{3 \times 7}{5 \times 7}+\frac{2 \times 5}{7 \times 5}\)
= \(\frac{21}{35}+\frac{10}{35}=\frac{31}{35}\)
Hence, total length of cloth bought by them = \(\frac{31}{35}\) m.
Subtraction of Unlike Fractions
To subtract unlike fractions, we first convert them into equivalent fractions with the same denominator (which is LCM of denominators) and then subtract them as like fractions.
Example 3.
Subtract the following.
(i) \(\frac{2}{3}\) from \(\frac{4}{5}\)
(ii) \(\frac{3}{7}\) from \(\frac{5}{9}\)
Solution:

Example 4.
A thread \(\frac{5}{9}\) m long cut into two pieces. One piece was \(\frac{1}{3}\) m long. How long is the other piece?
Solution:
Given, total length of a piece of thread = \(\frac{5}{9}\) m
Length of one piece of thread = \(\frac{1}{3}\) m
∴ Length of another piece = \(\left(\frac{5}{9}-\frac{1}{3}\right)\) m
LCM of 9 and 3 = 9
∴ \(\frac{5}{9}-\frac{1}{3}=\frac{5 \times 1}{9 \times 1}-\frac{1 \times 3}{3 \times 3}\)
\(\frac{5}{9}-\frac{3}{9}=\frac{2}{9}\)
Hence, the length of another piece of thread is \(\frac{2}{9}\) m.
Example 5.
Two kids Vehan and Vijay have a glass of the same size partly filled with milk. Vehan glass is \(\frac{5}{6}\)th full and Vijay’s glass is \(\frac{2}{5}\)th full. Whose glass is more full? By what fraction?
Solution:
The portion of Vehan’s glass filled by milk = \(\frac{5}{6}\) part
and the portion of Vijay’s glass filled by milk = \(\frac{2}{5}\) part
Now, LCM of 6 and 5 = 30
Equivalent fractions of \(\frac{5}{6}\) are \(\frac{5 \times 2}{6 \times 2}, \frac{5 \times 3}{6 \times 3}, \frac{5 \times 4}{6 \times 4}, \frac{5 \times 5}{6 \times 5}, \ldots \ldots \ldots \text { i.e. } \frac{10}{12}, \frac{15}{18}, \frac{20}{24}, \frac{25}{30}, \ldots\)
and equivalent fraction of \(\frac{2}{5}\) are \(\frac{2 \times 2}{5 \times 2}, \frac{2 \times 3}{5 \times 3}, \frac{2 \times 4}{5 \times 4}, \frac{2 \times 5}{5 \times 5}, \frac{2 \times 6}{5 \times 6}, \ldots \text { i.e. } \frac{4}{10}, \frac{6}{15}, \frac{8}{20}, \frac{10}{25}, \frac{12}{30}, \ldots\)
Here, equivalent fractions \(\frac{12}{30}\) and \(\frac{25}{30}\) have same denominator.
∵ 25 > 12
∴ \(\frac{25}{30}>\frac{12}{30} \text { i.e. } \frac{5}{6}>\frac{2}{5}\)
Now, \(\frac{5}{6}-\frac{2}{5}=\frac{25}{30}-\frac{12}{30}\) = \(\frac{13}{30}\)
Hence, Vehan’s glass is more full by fraction \(\frac{13}{30}\).
![]()
Example 6.
Complete the addition subtraction box.

Solution:

Hence, the required complete box is shown above.
Addition and Subtraction of Mixed Fractions
Firstly, we convert both mixed fractions into improper fractions and then add them by converting them into equivalent fractions with the same denominator. To subtract mixed fractions, we subtract smaller whole parts from greater whole parts and then subtract corresponding fractional parts. Mixed fractions can be written either as a whole part plus a proper fraction or entirely as an improper fraction. One way to add (or subtract) mixed fractions is to do the operation separately for the whole parts and the other way is to write the mixed fractions as improper fractions and then directly add (or subtract) them.
Example 7.
Add 2\(\frac{2}{5}\) and 3\(\frac{5}{6}\).
Solution:
We have, 2\(\frac{2}{5}\) and 3\(\frac{5}{6}\)
To add mixed fractions, first convert both mixed fractions into improper fractions.
Now, 2\(\frac{2}{5}\) = \(\frac{12}{5}\) and 3\(\frac{5}{6}\) = \(\frac{23}{6}\)
⇒ \(2 \frac{2}{5}+3 \frac{5}{6}=\frac{12}{5}+\frac{23}{6}\)
Now, convert them into equivalent fractions with the same denominator.
We have, \(\frac{12}{5}=\frac{12 \times 6}{5 \times 6}=\frac{72}{30}\) and \(\frac{23}{6}=\frac{23 \times 5}{6 \times 5}=\frac{115}{30}\) [∵ LCM of 5 and 6 is 30]
∴ \(2 \frac{2}{5}+3 \frac{5}{6}=\frac{72}{30}+\frac{115}{30}=\frac{187}{30}=6 \frac{7}{30}\)
Example 8.
Using Brahmagupta’s method, subtract 3\(\frac{5}{9}\) from 5\(\frac{1}{6}\).
Solution:
We have, 3\(\frac{5}{9}\) and 5\(\frac{1}{6}\)
To subtract mixed fractions, first convert both mixed fractions into improper fractions.

Example 9.
Simplify \(3 \frac{1}{3}+6 \frac{2}{3}-2 \frac{2}{3}\).
Solution:

Example 10.
What should be added to 7\(\frac{4}{15}\) to get 8\(\frac{2}{5}\).
Solution:
Let x be added to the 7\(\frac{4}{15}\),

Example 11.
Rahul was given 1\(\frac{1}{5}\) piece of bread and Garima was given 1\(\frac{1}{4}\) piece of bread. Find the total amount of bread that was given to both of them.
Solution:
Bread given to Rahul = 1\(\frac{1}{5}\) piece
Bread given to Garima = 1\(\frac{1}{4}\) piece.
Total bread given to both of them = 1\(\frac{1}{5}\) + 1\(\frac{1}{4}\)
= \(\frac{5 \times 1+1}{5}+\frac{4 \times 1+1}{4}\)
= \(\frac{6}{5}+\frac{5}{4}\)
LCM of 5 and 4 = 20
∴ \(\frac{6}{5}+\frac{5}{4}=\frac{6 \times 4}{5 \times 4}+\frac{5 \times 5}{4 \times 5}=\frac{24}{20}+\frac{25}{20}=\frac{24+25}{20}=\frac{49}{20}\)
Hence, total bread given to both of them = \(\frac{49}{20}\)
![]()
Example 12.
Add the difference of 1\(\frac{3}{4}\) and \(\frac{4}{5}\) to the sum of \(\frac{3}{5}\) and \(\frac{2}{7}\).
Solution:

Example 13.
Savita bought \(\frac{2}{5}\) m of ribbon and Kavita bought \(\frac{3}{4}\) m of the ribbon. What was the total length of the ribbon they bought?
Solution:
The ribbon bought by Savita = \(\frac{2}{5}\) m
The ribbon bought by Kavita = \(\frac{3}{4}\) m
∴ Total ribbon bought by them = \(\frac{3}{4}+\frac{2}{5}\)
LCM of 4 and 5 = 20
∴ \(\frac{3}{4}+\frac{2}{5}=\frac{3 \times 5}{4 \times 5}+\frac{2 \times 4}{5 \times 4}=\frac{15}{20}+\frac{8}{20}=\frac{23}{20} \mathrm{~m}\)
Hence, total ribbon bought by both = \(\frac{23}{20}\) m
Example Problems
Question 1.
Find the sum of the following.
(i) \(\frac{8}{9}\) and \(\frac{5}{12}\)
(ii) 8\(\frac{3}{4}\) and 10\(\frac{2}{5}\)
Solution:
(i) 1\(\frac{11}{36}\)
(ii) 19\(\frac{3}{20}\)
Question 2.
Subtract the following.
(i) \(\frac{5}{12}\) from \(\frac{7}{8}\)
(ii) \(\frac{1}{3}\) from \(\frac{7}{11}\)
Solution:
(i) \(\frac{11}{24}\)
(ii) \(\frac{10}{33}\)
Question 3.
What should be subtracted from \(\frac{7}{8}\) to get \(\frac{1}{4}\)?
Solution:
\(\frac{5}{8}\)
Question 4.
Mr. Kumar spent \(\frac{1}{8}\) of his salary on food, \(\frac{3}{8}\) of his salary on house, \(\frac{1}{4}\) of his salary on car. What fraction of his money was kept for savings?
Solution:
\(\frac{1}{4}\)
Question 5.
Nidhi and Neharika have bookshelves of the same size partly filled with books. Nidhi’s shelf is \(\frac{5}{6}\) full and Neharika’s shelf is \(\frac{2}{5}\) full. Whose bookshelf is less full and by what fraction is it less?
Solution:
Neharika, \(\frac{13}{30}\)
Question 6.
Add 2\(\frac{5}{7}\) and 7\(\frac{1}{9}\).
Solution:
\(\frac{619}{63}\)
Question 7.
Using Brahmagupta’s method subtract 3\(\frac{7}{9}\) from 5\(\frac{1}{11}\).
Solution:
\(\frac{130}{99}\)
Question 8.
Simplify \(4 \frac{1}{4}+7 \frac{3}{4}-3 \frac{2}{4}\).
Solution:
8\(\frac{2}{4}\)
Question 9.
What should be added to 1 to get 2\(\frac{3}{20}\)?
Solution:
1\(\frac{3}{20}\)
![]()
Question 10.
Two pipes are 5\(\frac{1}{3}\) m and 6\(\frac{1}{5}\) m long. If both are joined together, what will be the new length?
Solution:
11\(\frac{8}{15}\)
Question 11.
Add the difference of 1\(\frac{2}{3}\) and \(\frac{5}{7}\) to the sum of \(\frac{3}{7}\) and \(\frac{2}{3}\).
Solution:
2\(\frac{1}{21}\)
→ A fraction is a number representing a part of a whole. When some whole number of things/objects are shared equally among some number of people, then fractions tell us how much is the share of each.
→ It may be a single object or a group of objects. In a fraction, the numeral above the bar of the fraction is called the numerator whereas the numeral below the bar of the fraction is called the denominator.
Fraction \(=\frac{\text { Numerator }}{\text { Denominator }}\)
→ One-half is written as \(\frac{1}{2}\) and one-fourth as \(\frac{1}{4}\).\(\frac{3}{7}\) means three parts out of seven equal parts and \(\frac{5}{12}\) means five parts out of twelve equal parts.
→ A fraction having 1 as its numerator is called a unit fraction. The fractions in which the numerator is smaller than the denominator are called proper fractions.
→ The fractions having a numerator bigger than the denominator are called improper fractions.
→ A fraction is a part of a whole. The whole may be a single object or group of objects.
→ When one whole unit is divided into equal parts, then each part is called a fractional unit. ‘
→ Proper fractions are considered as those fractions in which the numerator is always less than the denominator.
![]()
→ Improper fractions are considered as those fractions in which the numerator is always greater than the denominator.
→ A fraction written as a combination of a whole number and a proper fraction is called a mixed fraction.
→ When two or more fractions represent the same share/number, they are called equivalent fractions.
→ To find an equivalent fraction of a given fraction, we may multiply or divide both the numerator and the denominator of the given fraction by the same number.
→ A fraction is said to be in its simplest form if its numerator and the denominator have no common factor other than 1.
→ To add or subtract, unlike fractions, first, we change them into like fractions and then perform the required operation.
→ When adding/sub-trading fractions, convert them into equivalent fractions with the same fractional unit (i.e., the same denominator), and then add/subtract the number of fractional units in each fraction to obtain the sum/difference.
→ This is accomplished by adding/subtracting the numerators while keeping the same denominator.
1. A fraction is a part of a whole number having a numerator and denominator.
For example: \(\frac{5}{7}\) where 5 is the numerator and 7 is the denominator.
2. Representation of a fraction on a number line.
For example: \(\frac{2}{3}\)

3. Proper fractions: Numerator is less than the denominator.
For example: \(\frac{2}{3}, \frac{5}{8} \text { and } \frac{1}{5}\)
4. Improper fractions: The Numerator is bigger than the denominator.
For example: \(\frac{5}{2}, \frac{7}{5}, \frac{10}{3} \text { and } \frac{6}{5}\)
5. Mixed fractions: It is represented by Quotient \(\frac{\text { Remainder }}{\text { Divisor }}\)
For example: \(5 \frac{1}{7}, 3 \frac{2}{3} \text { and } 4 \frac{5}{7}\)
6. Equivalent fractions: Two or more fractions are said to be equivalent fractions if they represent the same quantity.
For example: \(\frac{2}{5}, \frac{6}{15}, \frac{4}{10} \text { and } \frac{8}{20}\)
7. Simplest form of a fraction: A fraction is said to be simple if the numerator and the denominator have no common factor except 1.
For example: Simplest form of \(\frac{15}{20} \text { is } \frac{3}{4}\)
8. Like fractions: Two or more fractions having the same denominators are called like fractions.
For example: \(\frac{2}{5}, \frac{3}{5}, \frac{4}{5}, \frac{6}{5}\)
9. Unlike fractions: Two or more fractions having different denominators are called unlike fractions.
For example: \(\frac{8}{9}, \frac{5}{7}, \frac{6}{5}, \frac{7}{10}\)