Students rely on Class 6 Maths Extra Questions Chapter 7 Fractions Class 6 Extra Questions and Answers to improve their grades.
Class 6 Maths Chapter 7 Extra Questions Fractions
Class 6 Maths Fractions Extra Questions
NCERT Class 6 Maths Chapter 7 Fractions Extra Questions and Answers
Very Short Answer Type Questions
Question 1.
3 mm is what fraction of a metre?
Answer:
We know that 1 m = 1000 mm
3 mm = \(\frac{3}{1000}\) m
So, 3 mm is \(\frac{3}{1000}\) of a metre.
Question 2.
Write \(\frac{2}{3}\) of 60 kg.
Answer:
We have, \(\frac{2}{3}\) of 60 kg = \(\frac{2 \times 60}{3}\) = 2 × 20 = 40kg
Question 3.
What fraction of the week is 3 days?
Answer:
We know that 1 week = 7 days
∴ 3 days = \(\frac{3}{7}\) week
So, 3 days are \(\frac{3}{7}\) of a week.
Question 4.
30 seconds is what fraction of a minute?
Answer:
We know that 1 min = 60 s
i.e. 60s = 1 min
30 s = \(\frac{30}{60}\) min = \(\frac{1}{2}\) min
So, 30 sec are \(\frac{1}{2}\) of a minute.
![]()
Question 5.
Name the fraction which are always less than 1.
Answer:
We know that proper fractions are always less than 1.
Short Answer Type Questions
Question 1.
Write the natural numbers from 205 to 219. What fraction of them are odd numbers?
Answer:
Natural numbers from 205 to 219 are 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219.
Total natural numbers = 15
Odd numbers = 8
∴ Required fraction = \(\frac{\text { Odd numbers }}{\text { Natural numbers }}=\frac{8}{15}\)
Question 2.
What fraction of a kg is 650 gm?
Answer:
We know that 1 kg = 1000 g
∴ 650 gm = \(\frac{650}{1000}\) kg = \(\frac{65}{100}\)
= \(\frac{65 \div 5}{100 \div 5}\) [HCF of 65 and 100 is 5]
= \(\frac{13}{20}\)
So, 650 gm is \(\frac{13}{20}\) of a kg.
Question 3.
Find the fraction that represents the number of natural numbers to total numbers in the collection 0,1, 2, 3, 4, 5. What fraction will it be for whole numbers?
Answer:
Given collection is 0,1, 2, 3, 4, 5.
Natural numbers = 1, 2, 3, 4, 5
The fraction of natural numbers to the collection = \(\frac{5}{6}\)
Now, whole numbers = 0,1, 2, 3, 4, 5
The fraction of whole numbers to the collection = \(\frac{6}{6}\) i.e. \(\frac{1}{1}\)
Question 4.
Express the following as improper fraction.
(i) 5\(\frac{1}{4}\)
Answer:
We have,
Now, 5 \(\frac{1}{4}\) = 5 + \(\frac{1}{4}\) = \(\frac{5 \times 4+1}{4}=\frac{21}{4}\)
(ii) 7\(\frac{2}{3}\)
Answer:
We have, 7\(\frac{2}{3}\) = 7 + \(\frac{2}{3}=\frac{7 \times 3+2}{3}=\frac{23}{3}\)
Question 5.
Express the following as mixed fractions.
(i) \(\frac{15}{4}\)
Answer:
We have, improper fraction = \(\frac{15}{4}\)
∴ \(\frac{15}{4}=3 \frac{3}{4}\)
(ii) \(\frac{25}{6}\)
Answer:
We have, improper fraction = \(\frac{25}{6}\)
∴ \(\frac{25}{6}=4 \frac{1}{6}\)
Question 6.
Check whether the given fractions are equivalent.
(i) \(\frac{5}{7}, \frac{9}{12}\)
Answer:
We have,
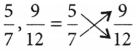
⇒ 5 × 12 = 9 × 7
60 ≠ 63
So, \(\frac{5}{7}, \frac{9}{12}\) are not equivalent fractions.
(ii) \(\frac{7}{5}, \frac{21}{15}\)
Answer:
We have,
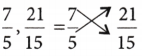
⇒ 7 × 15 = 105, 21 × 5 = 105
So, \(\frac{7}{5}, \frac{21}{15}\) are not equivalent fractions.
![]()
Question 7.
Find an equivalent fraction of \(\frac{2}{3}\) having denominator equal to 18.
Answer:

Question 8.
Write \(\frac{156}{60}\) in its lowest form.
Answer:
We have, \(\frac{156}{60}\)
Now, we find the HCF of 156 and 60.
∵ HCF of 156 and 60 is 12.
So, \(\frac{156}{60}=\frac{156 \div 12}{60 \div 12}=\frac{13}{5}\)
Question 9.
Compare 4\(\frac{2}{3}\) and 5\(\frac{3}{7}\).
Answer:

Question 10.
Find the value of the following:
(i) \(\frac{6}{17}+\frac{3}{17}+\frac{11}{17}\)
(ii) \(\frac{1}{2}+\frac{3}{4}+1 \frac{1}{3}\)
Answer:

Question 11.
Neelam’s father needs 1\(\frac{3}{4}\)m of cloth for the skirt of Neelam’s new dress and \(\frac{1}{2}\) m for the scarf. How much Cloth must he buy in all?
Answer:
Cloth required for skirt = 1\(\frac{3}{4}\) m
Cloth required for scarf = \(\frac{1}{2}\) m
. Total cloth = (1\(\frac{3}{4}\) + \(\frac{1}{2}\))m = \(\frac{7}{4}+\frac{1}{2}\)
\(\frac{7+2}{4}=\frac{9}{4}\) = 2\(\frac{1}{4}\) m
So, he must buy 2\(\frac{1}{4}\) m cloth.
Question 12.
Sunil purchased 12\(\frac{1}{2}\) of juice on Monday and 14\(\frac{3}{4}\)L of juice on Tuesday. How many litres of juice did he purchase together in two days?
Answer:
Sunil purchased juice on Monday = 12\(\frac{1}{2}\) L
Juice purchased on Tuesday = 14\(\frac{3}{4}\) L
∴ Total juice purchased = 12 \(\frac{1}{2}\) + 14\(\frac{3}{4}\) = \(\frac{25}{2}+\frac{59}{4}\)
= \(\frac{50+59}{4}=\frac{109}{4}\)
= 27\(\frac{1}{4}\) L
So, he purchased 27\(\frac{1}{4}\) L of juice in two days.
Question 13.
Using Brahmagupta’s method, simplify the following:
(i) 6 – \(\frac{3}{4}\)
Answer:
We have, 6 – \(\frac{3}{4}=\frac{6}{1}-\frac{3}{4}\)
= \(\frac{24-3}{4}=\frac{21}{4}\)
= 5\(\frac{1}{4}\)
(ii) \(\frac{7}{12}-\frac{4}{15}\)
Answer:
We have, \(\frac{7}{12}-\frac{4}{15}\)
= \(\frac{35-16}{60}=\frac{19}{60}\)
![]()
Question 14.
A cup is \(\frac{1}{3}\) full of milk. What part of the cup is still to be filled by milk to make it full?
Answer:
Given, cup is \(\frac{1}{3}\) full of milk.
∴ Required milk = 1 – \(\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\)
Hence, \(\frac{2}{3}\) part of the cup is required to make it full.
Question 15.
Mary bought 3\(\frac{1}{2}\) m of lace. She used 1\(\frac{3}{4}\) m of lace for her new dress. How much lace is left with her?
Answer:
Mary bought lace = 3\(\frac{1}{2}\) m
Lace used for new dress = 1\(\frac{3}{4}\) m
.’.Lace left with her
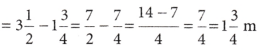
So, 1\(\frac{3}{4}\) m lace is left with her.
Question 16.
Nazima gave 2\(\frac{3}{4}\) L out of the 5\(\frac{1}{2}\) L of juice she purchased to her friends. How many litres of juice is left With her?
Answer:
Quality of Nazima has = 5\(\frac{1}{2}\)
She gave 2\(\frac{3}{4}\) L out of this to her friends.
Now, juice left with her = 5\(\frac{1}{2}-2 \frac{3}{4}=\frac{11}{2}-\frac{11}{4}\)
= \(\frac{22-11}{4}=\frac{11}{4}=2 \frac{3}{4}\)
So, 2\(\frac{3}{4}\) of juice is left with her.
Long Answer Type Questions
Question 1.
It was estimated that because of people switching to Metro trains, about 33000 tonne of CNG, 3300 tonne of diesel and 21000 tonne of petrol was saved by the end of year 2007.
Find the fraction of
(i) the quantity of diesel saved to the quantity of petrol saved.
(ii) the quantity of diesel saved to the quantity of CNG saved.
Answer:
Given, quantity of CNG saved = 33000 tonne
Quantity of diesel saved = 3300 tonne
Quantity of petrol saved = 21000 tonne
(i) The fraction of the quantity of diesel saved to the quantity of petrol saved = \(\frac{3300}{21000}=\frac{33}{210}=\frac{33 \div 3}{210 \div 3}\)
[∵ HCF of 33 and 210 is 3]
(ii) The fraction of the quantity of diesel to the quantity of CNG saved = \(\frac{3300}{33000}=\frac{33}{330}=\frac{33 \div 33}{330 \div 33}=\frac{1}{10}\)
Question 2.
Poorvi cut a cake into 8 equal pieces. If she wanted to divide each of them into 3 equal pieces, what fraction of the whole cake would each small pieces be?
Answer:
Number of pieces in which the cake cut = 8
Number of pieces each cut piece divided into = 3
∴ Total number of pieces = 8 × 3 = 24
Hence, each piece is represented by the fraction
Question 3.
Energy content of different foods are as follows:
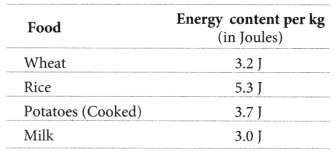
Which food provides the least energy and which provides the maximum? Also, express the least energy as a fraction of the maximum energy.
Answer:
In the given table, we see that the minimum value is 3.0 J and maximum value is 5.3 J.
∴ Least energy provide by food = 3.0 J i.e. Milk
Food which provide the maximum energy = 5.3 J i.e. Rice
∴ Required fraction = \(\frac{\text { Least energy }}{\text { Maximum energy }}=\frac{3.0}{5.3}=\frac{30}{53}\)
![]()
Question 4.
A rectangle is divided into certain number of equal parts. If 16 of the parts so formed represent the fraction \(\frac{1}{4}\), find the number of parts in which the rectangle has been divided.
Answer:
Let a rectangle be divided into x equal parts.
Now, 16 of the parts represent =
∴ \(\frac{16}{x}=\frac{1}{4}\) ⇒ x =16 × 4 ⇒ x = 64 parts × 4
Hence, rectangle is divided into 64 equal parts.
Question 5.
From school X out of 750 students, 250 were selected for an essay writing and from another school V out of 1200 students, 300 were selected. From which school, more students were selected?
Answer:
Total students in school X = 750
Selected students = 250
∴ Fraction of selected students to the total students
= \(=\frac{250}{750}=\frac{1}{3}\) ……….(i)
Now, total students in school Y = 1200 Selected students = 300
∴ Fraction of selected students to the total students
= \(\frac{300}{1200}=\frac{1}{4}\)
From Eqs. (i) and (ii), \(\frac{1}{3}>\frac{1}{4}\) [∵ 4 > 3]
Hence, from the school X more students were selected.
Question 6.
The fish caught b, Neetu was of weight 3\(\frac{3}{4}\) kg and the fish caught by Narendra was of weight 2\(\frac{1}{2}\) kg. How much more was Neetu’s fish weight than that of Narendra?
Answer:
Given, weight of fish caught by Neetu = 3\(\frac{3}{4}\) kg = \(\frac{15}{4}\) kg
and weight of the fish caught by Narendra = 2 \(\frac{1}{2}\) = \(\frac{5}{2}\) kg
Difference between their weights
= \(\frac{15}{4}-\frac{5}{2}=\frac{15}{4}-\frac{5 \times 2}{2 \times 2}\)
= \(\frac{15}{4}-\frac{10}{4}=\frac{15-10}{4}=\frac{5}{4}\)kg
Hence, Neetu’s fish weight is \(\frac{5}{4}\) kg more than the Narendra’s fish weight.
Question 7.
On an average, \(\frac{1}{10}\) of the food eaten is turned into organism’s own body and is available for the next level of consumer in a food chain. What fraction of the food eaten is not available for the next level?
Answer:
Quantity of food eaten which turned into organism’s own body = \(\frac{1}{10}\) of the total food
Now, the quantity of food eaten which is not available 1 10 -1 9
for the next level = 1 – \(\frac{1}{10}=\frac{10-1}{10}=\frac{9}{10}\)
Hence, the required fraction = \(\frac{9}{10}\)
Question 8.
Mr. Rajan got a job at the age of 24 yr and he got retired from the job at the age of 60 yr. What fraction of his age till retirement was he in the job?
Answer:
Given, Rajan’s age on the joining = 24 yr
and retirement age = 60 yr
The number of years, he did the job
= Retirement age – Joining age
= 60 – 24 = 36 yr
∴ The fraction of his age till retirement, when he was in the job
= \(\frac{\text { Total years he did the job }}{\text { Retirement age }}=\frac{36}{60}\)
= \(\frac{36 \div 12}{60 \div 12}=\frac{3}{5}\)
Hence, the required fraction is \(\frac{3}{5}\).
![]()
Question 9.
Roma gave a wooden board of length 150 \(\frac{1}{4}\) cm to a carpenter for making a shelf. The carpenter sawed off a 1 piece of 40 \(\frac{1}{5}\) cm from it. What is the length of the 5 remaining piece?
Answer:
Given, length of a wooden board
= 150\(\frac{1}{4}\) cm = \(\frac{601}{4}\) cm
Carpenter sawed off a piece of wooden board
= 40\(\frac{1}{5}\) cm = \(\frac{201}{5}\)cm
Length of the remaining piece = \(\frac{601}{4}-\frac{201}{5}\)
∴ LCM of 4 and 5 = 20
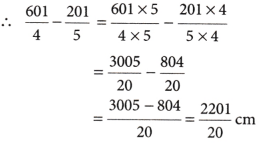
Hence, the length of remaining piece is \(\frac{2201}{2}\) cm or 110\(\frac{1}{20}\)cm.
Case-Based Questions
Question 1.
Cross country is a running even in which runners completed a pre-decided distance.
It includes different activities in which runners cover different environments. A cross country running event of 11 km is as follows.
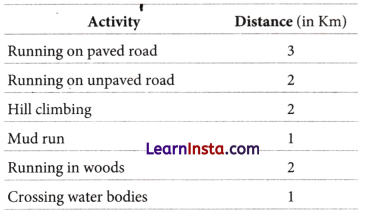
(i) What fraction of the total distance is the mud run?
(a) \(\frac{11}{1}\)
(b) \(\frac{1}{10}\)
(c) \(\frac{1}{11}\)
(d) 1
Answer:
(c) Total distance runner covers = 11 km
Distance in mud run = 1 km
∴ Fraction of total distance in mud run
= \(=\frac{\text { Distance in mud run }}{\text { Total distance runner covers }}=\frac{1}{11}\)
(ii) What fraction of the total distance is the distance covered on paved and unpaved roads?
(a) \(\frac{3}{2}\)
(b) \(\frac{5}{5}\)
(c) \(\frac{5}{6}\)
(d) \(\frac{5}{11}\)
Answer:
(d) Distance in paved road = 3 km.
Distance in unpaved road = 2 km.
∴ Total distance in both = \(\frac{3+2}{11}=\frac{5}{11}\)
Question 2.
Katherine completed the cross country in 1 hr. She completed the run on the paved and unpaved roads in one-fourth of an hour while Juliana covered it in half an hour.
(i) In how many minutes did Katherine cover the distance on the paved and unpaved roads?
(a) 10 min
(b) 15 min
(c) 20 min
(d) 30 min
Answer:
(b) Katherine completed the cross country = 1 hr
∵ Katherine covered the run on the paved and unpaved roads in one-fourth of an hour, which is equal to
\(\frac{1}{4}\) × 1 h = \(\frac{1}{4}\) × 60 min = 15 min
Thus, Katherine coveres the distance on paved and unpaved roads in 15 min.
(ii) How much more time (in hrs) was taken by Juliana than Katherine?
Answer:
Katherine completed the run on the paved and
unpaved road = \(\frac{1}{4}\) of 1h = \(\frac{1}{4}\) × 60 min = 15 min
While Juliana covered the run on the paved and
unpaved road = \(\frac{1}{2}\) of 1h = \(\frac{1}{2}\) × 60 min = 30 min
Thus, Juliana time – Katherine time
= (30 – 15) = 15 min
Thus, Juliana takes 15 min or \(\frac{1}{4}\) of an hour more than Katherine.
Question 3.
Parul and two of her friends share a pizza equally among themselves.
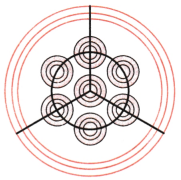
(i) Parul says, ‘Here are three equal halves of the pizza.’ Is Parul’s statement correct? Give reasons.
Answer:
No, Parul’s statement is not correct. Pizza is divided into three equal parts, which is not half of the pizza.
(ii) Which fraction represents one part of the whole pizza?
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) 3
Later, three more friends join Parul. Parul divides the pizza again to have 6 parts.
Answer:
(b) Pizza divided into 3 parts.
Therefore, one part of pizza = \(\frac{1}{3}\).
(iii) Does every one get an equal portion? Give reasons.
Answer:
Three more friends joined Parul means now remaining pizza is divided again.
So, everyone does not get an equal portion of pizza.
(iv) Suggest a way to divide the pizza into six equal parts.
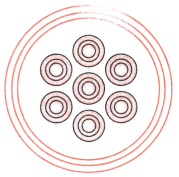
Answer:
Usually pizzas are circular. Therefore, total angle = 360°
To divide 360 into 6 parts divide 360 by 6 = 60°
i.e \(\frac{360^{\circ}}{6}\) = 60°
Now, measure 60° and cut the pizza into 6 equal parts.
![]()
Skill Based Questions
Question 1.
Across
1. A fraction is a number representing part of a ___.
2. One unit is divided into several equal parts, each part is called a ___ unit.
3. \(\frac{5}{2}\) of a number is equal to five times ___ of a number.
4. Number of whole units in \(\frac{7}{2}\) is ___
Down
5. \(\frac{1}{3}\) and \(\frac{2}{6}\) are fractions.
6. If numerator and denominator have no common factor except 1, then the fraction is said to be in ___ form.
7. Fraction \(\frac{1}{3}, \frac{1}{5}, \frac{1}{8}\) are in ___ order.

Answer:
Across
1. Whole
2. Fractional
3. Half
4. Three
Down
5. equivalent
6. Lowest
7. Descending
Class 6 Maths Chapter 7 Extra Questions in Hindi भिन्न
Fractions Class 6 Extra Questions in Hindi
बहुविकल्पीय प्रश्न
प्रश्न 1.
छायांकित भाग को दर्शाने वाली भिन्न

है
(a) \(\frac{1}{4}\)
(b) \(\frac{3}{4}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{8}\)
उत्तर:
(a) \(\frac{1}{4}\)
प्रश्न 2.
छायांकित भाग को दर्शाने वाली भिन्न

है
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{6}\)
(d) इनमें से कोई नहीं
उत्तर:
(c) \(\frac{1}{6}\)
प्रश्न 3.
छायांकित भाग को दर्शाने वाली भिन्न

है
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{8}\)
उत्तर:
(d) \(\frac{1}{8}\)
प्रश्न 4.
25 पैसे, रु 1 का कितना अंश है?
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{8}\)
(d) \(\frac{1}{10}\)
उत्तर:
(b) \(\frac{1}{4}\)
प्रश्न 5.
निम्नलिखित में से कौन-सी उचित भिन्न है जिसका अंश 1 व हर 3 है?
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{1}{9}\)
(d) \(\frac{1}{12}\)
उत्तर:
(a) \(\frac{1}{3}\)
![]()
प्रश्न 6.
\(\frac{5}{2}\) को मिश्रित भिन्न के रूप में व्यक्त करें।
(a) 1\(\frac{1}{2}\)
(b) 2\(\frac{1}{2}\)
(c) 3\(\frac{1}{2}\)
(d) 4\(\frac{1}{2}\)
उत्तर:
(b) 2\(\frac{1}{2}\)
प्रश्न 7.
\(\frac{9}{4}\) को मिश्रित भिन्न के रूप में व्यक्त करें।
(a) 2\(\frac{1}{4}\)
(b) 3\(\frac{1}{4}\)
(c) 4\(\frac{1}{4}\)
(d) 5\(\frac{1}{4}\)
उत्तर:
(a) 2\(\frac{1}{4}\)
प्रश्न 8.
मिश्रित भिन्न 2\(\frac{3}{4}\) को अनुचित भिन्न के रूप में व्यक्त करें
(a) \(\frac{11}{4}\)
(b) \(\frac{4}{11}\)
(c) \(\frac{9}{11}\)
(d) \(\frac{7}{11}\)
उत्तर:
(a) \(\frac{11}{4}\)
प्रश्न 9.
\(\frac{45}{20}\) का सरलतम रूप है
(a) \(\frac{9}{4}\)
(b) \(\frac{4}{9}\)
(c) \(\frac{9}{8}\)
(d) \(\frac{2}{9}\)
उत्तर:
(a) \(\frac{9}{4}\)
प्रश्न 10.
\(\frac{3}{4}\) समतुल्य भिन्न कौन-सी है?
(a) \(\frac{6}{11}\)
(b) \(\frac{9}{10}\)
(c) \(\frac{15}{20}\)
(d) \(\frac{21}{25}\)
उत्तर:
(c) \(\frac{15}{20}\)
प्रश्न 11.
\(\frac{2}{5}\) के तुल्य भिन्न जिसका अंश 4 है,
(a) \(\frac{4}{10}\)
(b) \(\frac{4}{12}\)
(c) \(\frac{4}{16}\)
(d) \(\frac{4}{20}\)
उत्तर:
(a) \(\frac{4}{10}\)
प्रश्न 12.
\(\frac{20}{36}\) के तुल्य भिन्न जिसका हर 9 है
(a) \(\frac{4}{9}\)
(b) \(\frac{5}{9}\)
(c) \(\frac{7}{9}\)
(d) \(\frac{8}{9}\)
उत्तर:
(b) \(\frac{5}{9}\)
![]()
प्रश्न 13.
निम्न में से कौन-सा युग्म तुल्य नहीं है?
(a) \(\frac{1}{2}\), \(\frac{2}{3}\)
(b) \(\frac{4}{5}\), \(\frac{12}{15}\)
(c) \(\frac{6}{7}\), \(\frac{12}{14}\)
(d) \(\frac{4}{9}\), \(\frac{36}{81}\)
उत्तर:
(a) \(\frac{1}{2}\), \(\frac{2}{3}\)
प्रश्न 14.
निम्न में से कौन-सा युग्म अनुचित भिन्न है?
(a) \(\frac{2}{3}\), \(\frac{3}{5}\)
(b) \(\frac{1}{7}\), \(\frac{6}{7}\)
(c) \(\frac{2}{9}\), \(\frac{5}{9}\)
(d) \(\frac{4}{13}\), \(\frac{12}{13}\)
उत्तर:
(a) \(\frac{2}{3}\), \(\frac{3}{5}\)
प्रश्न 15.
अपाला ने 100 पृष्ठों वाली एक पुस्तक के 50 पृष्ठ टाइप किए। मीनू ने उसी पुस्तक के 25 पृष्ठ टाईप किए। पुस्तक के पृष्ठों का अधिक अंश किसने टाइप किया?
(a) अपाला
(b) मीनू
(c) न तो (a) न तो (b)
(d) कह नहीं सकते
उत्तर:
(a) अपाला
प्रश्न 16.
\(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) =
(a) 1
(b) 2
(c) 4
(d) 8
उत्तर:
(a) 1
प्रश्न 17.
1 – \(\frac{1}{2}\) =
(a) \(\frac{1}{2}\)
(b) 1
(c) –\(\frac{1}{2}\)
(d) \(\frac{1}{4}\)
उत्तर:
(a) \(\frac{1}{2}\)
![]()
प्रश्न 18.
\(\frac{8}{15}\) – ? = \(\frac{7}{15}\)
(a) \(\frac{1}{15}\)
(b) \(\frac{2}{15}\)
(c) –\(\frac{4}{15}\)
(d) \(\frac{7}{15}\)
उत्तर:
(a) \(\frac{1}{15}\)
प्रश्न 19.
एक शिक्षक ने अपने कार्य का \(\frac{3}{4}\) भाग पूरा कर लिया। अब कितना पाठ्यक्रम शेष है?
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{6}\)
(d) \(\frac{1}{3}\)
उत्तर:
(b) \(\frac{1}{4}\)
प्रश्न 20.
मनीष एक किताब का \(\frac{5}{6}\) भाग पढ़ता है। प्रीति एक किताब का \(\frac{1}{6}\) भाग पढ़ती है। मनीष द्वारा कितना अधिक भाग पढ़ा गया।
(a) \(\frac{2}{3}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{5}{6}\)
(d) इनमें से कोई नहीं
उत्तर:
(a) \(\frac{2}{3}\)