Here we are providing Class 11 chemistry Important Extra Questions and Answers Chapter 5 States of Matter. Chemistry Class 11 Important Questions are the best resource for students which helps in Class 11 board exams.
Class 11 Chemistry Chapter 5 Important Extra Questions States of Matter
States of Matter Important Extra Questions Very Short Answer Type
Question 1.
What is the pressure of a gas? What is its S.I. unit?
Answer:
The force exerted by the gas molecules per unit area on the walls of the container is equal to its pressure SI. unit of pressure is the pascal (Pa).
1 Pa = Nm2- =1 kg m-1s-2.
Question 2.
What does the temperature of gas represent?
Answer:
The temperature of the gas represents the average kinetic energy of the gas molecules as we know K.E. ∝ \(\sqrt{T}\).
Question 3.
Why is it not possible to cool gas to o K?
Answer:
This is because all gases condense to liquids or solids before this temperature is reached.
Question 4.
What property of molecules of real gases is indicated by van der Waal’s constant ‘a’?
Answer:
Intermolecular attraction.
Question 5.
What do you understand by standard temperature?
Answer:
The standard temperature is 0°C or 273 K.
Question 6.
What is the effect of temperature on the vapour pressure of a liquid?
Answer:
Vapour pressure increases with rising in temperature.
Question 7.
What is an ideal gas equation?
Answer:
For given ideal gas PV = nRT
where P = gas pressure;
V = volume,
R = gas constant
T = Temp. (Kelvin scale);
n – no. of moles of gas.
Question 8.
Which state of matter has a definite volume, but no definite shape?
Answer:
Liquid.
Question 9.
What is the value of the gas constant in S.I. units?
Answer:
8.314 JK-1 mol-1.
Question 10.
What are the S.I. units of surface tension?
Answer:
Nm-1
Question 11.
What is the compressibility factor?
Answer:
Z = \(\frac{PV}{nRT}\).
Question 12.
What is the equation of state for real gases?
Answer:
van der Waal’s equation(P + \(\frac{a}{\mathrm{~V}^{2}}\))(v – b) = RT for 1 mole.
Question 13.
How is the pressure of a gas related to its density at a particular temperature?
Answer:
d = \(\frac{MP}{RT}\)
In underwater diving the physiological effects of individual component gases of breathing gases is a function of partial pressure formula.
Question 14.
How is the partial pressure of a gas in a mixture related to the total pressure of the gaseous mixture?
Answer:
The partial pressure of a gas = Mole fraction of that gas × total pressure.
Question 15.
What is the relationship between average kinetic energy , and the temperature of a gas?
Answer:
K.E. = \(\frac{3}{2}\)kT
where k is Boltzmann constant = \(\frac{\mathrm{R}}{\mathrm{N}_{0}}\).
Question 16.
What is the significance of van der Waal’s constant ‘a’ and ‘b’?
Answer:
‘a’ is a measure of the magnitude of the intermolecular forces of attraction while ‘b’ is a measure of the effective size of the as molecules.
Question 17.
Arrange the solid, liquid and gas in order of energy-giving reasons.
Answer:
Solids < liquid < gas. This is because a solid absorbs energy to change into a liquid which further absorbs energy to change into a gas.
Question 18.
What is the effect of pressure on the boiling point of a liquid?
Answer:
The boiling point increases as the prevailing pressure increases.
Question 19.
Why are vegetables cooked with difficulty at a hill station?
Answer:
The atmospheric pressure decreases as we go up. Therefore at the hills due to the lowering of atmospheric pressure, boiling points lowered.
Question 20.
The size of the weather balloon keeps on becoming larger as it rises to high altitude. Explain why?
Answer:
At higher altitudes, the external pressure on the balloon decreases and therefore, its size increases.
Question 21.
How is the pressure of a given sample of a gas related to the temperature at a constant volume?
Answer:
P ∝ T, i.e., Pressure varies as absolute temperature.
Question 22.
How is the pressure of a gas related to the number of molecules of a gas at constant volume and temperature?
Answer:
P ∝ N; N = No. of molecules of a gas.
Question 23.
What type of graph do we get when we plot a graph PV against P? What is shown by this graph?
Answer:
It is a straight line parallel to the r-axis. It shows that PV is constant at different pressures. It shows Boyle’s Law.
Question 24.
At what temperature will oxygen molecules have the same kinetic energy as ozone molecules at 30°C?
Answer:
AT 30°C. Kinetic energy depends only on the absolute temperature and not on the identity of the gas.
Question 25.
At a particular temperature why vapours pressure of acetone is less than that of ether?
Answer:
This is because intermolecular forces in acetone are more than those present in ether.
Question 26.
Out of NH3 and N2 which will have
(i) a larger value of V and
Answer:
NH3 will have a large value of ‘a’ because of hydrogen bonding.
(ii) larger value of ‘b’?
Answer:
N2 should have a large value of ‘b’ because of its larger molecular size.
Question 27.
Why are the gases helium and hydrogen not liquefied at room temperature by applying very high pressure?
Answer:
Because their critical temperature is lower than room temperature. Gases cannot be liquefied above the critical temperature by applying even very high pressure.
Question 28.
What will boil at a higher temperature at sea level or at the top of mountains?
Answer:
Water will boil at a higher temperature at sea level.
Question 29.
Under what conditions do real gases tend to show ideal gas behaviour?
Answer:
When the pressure of the gas is very low and the temperature is high.
Question 30.
Both propane (C3Hg) and carbon dioxide (CO2) diffuse at the same rate under identical conditions of temperature and pressure. Why?
Answer:
Both propane (C3Hg) and carbon dioxide (CO2) have the same molar mass (44 gm).
Question 31.
If the number of moles of a gas is doubled by keeping the temperature and pressure constant, what will happen to the volume?
Answer:
The volume will also double as V ∝ n according to Avogadro’s Law.
Question 32.
What is a Triple point?
Answer:
The temperature at which solid, liquid and vapour; i.e., all the three states of the substance exist together is called the triple point.
Question 33.
Is Dalton’s law of partial pressures valid for a mixture of SO2 and O2?
Answer:
No, the law holds good only for those gases which do not react with each other.
Question 34.
Under what conditions a gas deviates from ideal gas behaviour?
Answer:
It deviates at low temperature and high pressure.
Question 35.
Molecule A is twice as heavy as molecule B. Which of these has higher kinetic energy at any temperature?
Answer:
K.E. of a molecule is directly proportional to temperature and is independent of its mass. So both the molecule A and B at any temperature will have equal kinetic energy.
Question 36.
How will you define pascal?
Answer:
It is defined as the pressure exerted by a force of one newton on an area of one meter2.
Pa = 1 Nm-2.
Question 37.
How will you define London or dispersion forces?
Answer:
The forces of attraction between the induced momentary dipoles are called London or dispersion forces.
Question 38.
What is Absolute Zero?
Answer:
The lowest possible hypothetical temperature of – 273°C at which gas is supposed to have zero volume is called Absolute zero.
Question 39.
What is the nature of the gas constant R?
Answer:
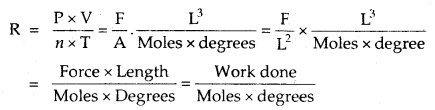
= work done per degree per mole.
Question 40.
What is the value of R in SI units?
Answer:
R = 8.314 JK-1 mol-1 = 8.314 k Pa dm3 K-1 mol-1
Question 41.
What is meant from Boyle point or Boyle temperature?
Answer:
The temperature at which a real gas behaves like an ideal gas over an appreciable pressure range is called Boyle point or Boyle temperature.
Question 42.
How will you define viscosity?
Answer:
The internal resistance to the flow of a fluid is called its viscosity.
Question 43.
What is the effect of temperature on the viscosity of a liquid?
Answer:
The viscosity of a liquid decreases with an increase in temperature.
Question 44.
How will you convert pressure in atmospheres into SI units?
Answer:
1 atm = 1,01,325 Pa or Nm-2 or 1 bar = 105 Pa.
Question 45.
What do you understand from surface tension?
Answer:
The surface tension of a liquid is defined as the force acting at right angles to the surface along a one-centimetre length of the. liquid.
Question 46.
What is the effect of the increase in temperature on the surface tension of a liquid?
Answer:
Surface tension decreases in increasing the temperature.
Question 47.
What is the difference between normal boiling point and standard boiling point?
Answer:
When the external pressure is equal to one atmospheric pressure the boiling point is referred to as a normal boiling point, when it is one bar, the boiling point is called its standard boiling point.
Question 48.
What is the difference between vapour and gas?
Answer:
When gas is below its critical temperature, it is called vapour.
Question 49.
What happens if a liquid is heated to the critical temperature of its vapours?
Answer:
The meniscus between the liquid and the vapour disappears, the surface tension of the liquid becomes zero.
Question 50.
Why falling liquid drops are spherical?
Answer:
The surface area of a sphere is minimum. In order to have minimum surface area drops of the liquid become spherical.
States of Matter Important Extra Questions Short Answer Type
Question 1.
Ammonia and Sulphur dioxide gases are prepared in two comers of a laboratory. Which gas will be detected first by a student working in the middle of the laboratory and why?
Answer:
Molecular mass of NH3 = 17 Molecular mass of SO2 = 64
NH3 is a lighter gas and diffuses at a faster speed than SO2
∴ NH3 gas will be detected first.
[∵ Acc. to Graham’s law of diffusion \(\frac{r_{1}}{r_{2}}=\sqrt{\frac{d_{2}}{d_{1}}}\)
Question 2.
What is the effect of hydrogen bonding on the viscosity of a liquid?
Answer:
Hydrogen bonding leads to an increase in the effective size of the moving unit in the liquid. Due to an increase in the size and mass of the molecule, there is greater interval resistance of the flow of the liquid. As a result, the viscosity of the liquid rises.
Question 3.
Which are the two faulty assumptions in the kinetic theory of gases.
Answer:
- There is no force of attraction between the molecules of the gas.
- The volume of the molecules of the gas is negligibly small as compared to the total space (volume) occupied by the gas.
Question 4.
What is the relationship between the density and molar mass of a gaseous substance? Derive it.
Answer:
Ideal gas equation is PV = nRT
or \(\frac{n}{V}=\frac{p}{R T}\)
Replacing n by \(\frac{m}{M}\), we get
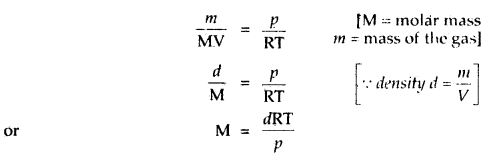
Question 5.
What is meant by the term: Non-ideal or real gas?
Answer:
The gas which does not obey the Cas law:
Boyle’s law, Charles’ law, Avogadro^ law at all temperatures and pressures is a called-non-ideal or real gas. Most of the real gases show ideal behaviour at low pressure and high temperature.
Question 6.
Derive the ideal gas equation PV = nRT.
Answer:
According to Boyle’s law V ∝ \(\frac{1}{P}\) if n and T are constant.
According to Charles’ law V ∝ T at constant P.and n
According to Avogadro’s law V ∝ n at constant T and P
Combining the three laws
In
V ∝ \(\frac{Tn}{P}\)
or
PV ∝ nT
or
PV = nRT where R is a constant of proportionality called universal gas constant.
Question 7.
Why liquids have a definite volume, but no definite shape?
Answer:
It is due to the fact that in liquids intermolecular forces are strong enough to hold the molecules together, but these are strong enough to hold the molecules together, but these forces are not strong enough to fix them into definite or concrete positions as in solids. Hence they possess fluidity but no definite shape.
Question 8.
How do the real gases deviate from ideality above and below the Boyle point?
Answer:
Above their Boyle point, real gases show positive deviations from ideality and the values of Z are greater than one. The forces of attraction between the molecules are very feeble. Below the Boyle point, real gases first show a decrease, in Z value with increasing pressure, the value Of Z increases continuously.
Question 9.
Write down the van der Waals, equation for n moles of a real gas. What do the constants ‘a’ and ‘b’ stand for?
Answer:
(P + \(\frac{a n^{2}}{V^{2}}\)) (V – nb) = nRT
where p, Vindicate gas pressure and its volume. T is the Kelvin temperature of the gas. R is gas constant. Value of ‘a’ is a measure of the magnitude of intermolecular attractive forces within the molecule and is independent of temperature and pressure, ‘rib’ is approximately the total volume occupied by the molecules themselves. ‘a’ and ‘b’ are called van der Waals constants and their value depends upon the nature of the gas.
Question 10.
How is compressibility factor Z related to the real and ideal volume of the gas?
Answer:
Z = \(\frac{P \mathrm{~V}_{\text {real }}}{n \mathrm{RT}}\) …(1)
If the gas shows ideal behaviour, then
Videal = \(\frac{nRT}{P}\) ….(2)
On putting the titis value of nRT in equation (1), we get
Z = \(\frac{\mathrm{V}_{\text {real }}}{\mathrm{V}_{\text {ideal }}}\)
Thus the compressibility factor Z is the ratio of the actual molar volume of a gas to the molar volume of it. if it were an ideal gas at that temperature and pressure.
Question 11.
What do the critical temperature, critical pressure, and critical volume for a gas stand for?
Answer:
The critical temperature is the temperature above which a gas cannot be liquified however large may be the pressure applied on it. The pressure sufficient to liquiíy a gas at its critical temperature is called its critical pressure. The volume of the gas at its crìtical temperature is called its critical volume’.
Question 12.
What do the absolute zero and absolute scale of temperature stand for?
Answer:
The lowest possible hypothetical temperature of – 273°C at which gas is supposed to have zero volume is called Absolute! zero.
Lord Kelvin suggested a new scale of temperature starting with – 273°C and it’s zero. This scale of temperature is called the absolute scale of temperature.
Absolute or Kelvin temperature is given by T, where
T = t°C + 273
t°C stands for the centigrade scale of temperature.
Question 13.
Give one application of Dalton’s law of partial pressures.
Answer:
One application of Dalton’s law of partial pressures is in determining the/pressure of dry gas. Gases are generally collected over water and, so they contain water vapours. The pressure exerted by the water Vapours at-a particular temperature is called the Aqueous Tension. By subtracting the aqueous tension from the ‘ vapour pressure of the moist gas, the pressure of the dry gas can be calculated.
Pdry gas= Pmoist gas – Aqueous Tension (at t°C).
Question 14.
How will you calculate the partial pressure of gas using Dalton’s Law of partial pressures?
Answer:
In a mixture of non-reacting gases A, B, C etc., if each gas is considered to be an ideal gas, then
PA = nA \(\frac{RT}{V}\)
PB = nB \(\frac{RT}{V}\)
PC = nC \(\frac{RT}{V}\)
where nA, nB nC stand for their respective moles in the same vessel .
[V = constant, keeping T constant]
Then according to Dalton’s law ‘
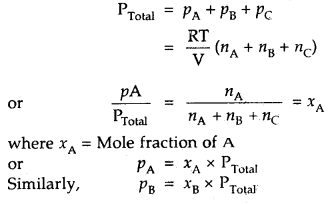
Thus, particle pressure of a. gas – Mole fraction of A × Total pressure.
Question 15.
Is there any effect of the nature of a liquid and temperature on the surface tension of a liquid?
Answer:
- Effect of nature of the liquid: Surface tension is a property that arises due to the intermolecular forces of attraction among the molecules of the liquid.
- The surface tension of the liquids generally decreases with an increase in temperature and becomes zero at the critical temperature.
Question 16.
Leaving electrostatic forces that exist between oppositely charged ions, which other intermolecular attractive forces exist between atoms or ions. Mention them.
Answer:
- van der Waals forces
- London Forces or Dispersion Forces
- Dipole-dipole forces
- Dipole-induced dipole forces
- Hydrogen bond.
Question 17.
What is the relationship between intermolecular forces and thermal interactions?
Answer:
Intermolecular forces tend to keep the molecules together but the thermal energy of the molecules tends to keep them apart. Three states of matter are the result of a balance between intermolecular forces and the thermal energy of the molecules.
Gas → Liquid → Solid
intermolecular forces increases →
Gas ← Liquid ← Solid
increase in Thermal energy ←
Question 18.
What are the main characteristics associated with gases?
Answer:
- Gases are highly compressible.
- Gases exert pressure equally in all directions.
- Gases have a much lower density than solids or liquids.
- Gases do not have definite shape and volume.
- Gases intermix freely and completely in all proportions.
Question 19.
What do you understand by the term? Isotherms and Isobars?
Answer:
Isotherms are the curves plotted by varying pressure against volume keeping temperature constant.
Each line obtained by plotting volume against temperature keeping, pressure constant is called an Isobar.
Question 20.
What are the forces which are responsible for the viscosity of a liquid? Why is glycerol more viscous than water?
Answer:
The forces responsible for the viscosity of the liquids are
- Hydrogen bonding
- van der Waals torches.
Glycerol possesses greater viscosity than water because glycerol has extensive hydrogen bonding in its molecules due to the pressure of three-Oil groups in it as compared to the hydrogen bonding in water molecules.
States of Matter Important Extra Questions Long Answer Type
Question 1.
Derive the Ideal gas equation PV = nRT.
Answer:
Let a certain mass of a gas at pressure P1 and temperature
T1 occupy a volume V1. On changing the pressure and temperature respectively to P2 and T2, let the volume of the gas change to V2.
(i) Let us first change the pressure P1 to P2 at constant temperature T1. Then, according to Boyle’s law, volume V is given by,
P2V = P1V1
or
V = \(\frac{P_{1} V_{1}}{P_{2}}\) …(1)
(ii) Now keeping the pressure constant at P2, heat the gas from temperature T1 to T2, the volume changes from V to V2.
By Charle’s Law, we must have,
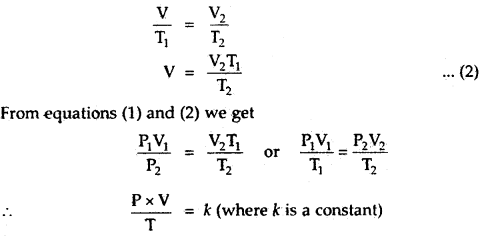
The numerical value of k depends upon the amount of gas and the units in which P and V are expressed. By Avogadro’s law, for one mole of any gas, the value of \(\frac{PV}{T}\) will be the same and is represented
\(\frac{PV}{T}\) = R
or
PV = RT.
for n moles of an ideal gas
PV = nRT
Question 2.
State the fundamental assumptions of the kinetic theory of gases
Or
What are the postulates of the kinetic theory of gases?
Or
Write a short note on “Microscopic Model of a gas”.
Answer:
To explain the general properties of gases to provide some theoretical explanation for various gas laws (stated on basis of experimental studies), various, scientists Bernoulli, Clausius, Maxwells, Boltzmann and others, gave ‘Kinetic Theory of Gases’ which explains qualitatively as well as quantitatively the various aspects of gas behaviour.
The important postulates of the theory are:
- All gases are made up of a very large number of minutes particles called molecules.
- The molecules are separated from one another by large distances. The empty spaces among the molecules are so large that the actual volume of the molecules is negligible as compared to the total volume of the gas.
- The molecules are in a state of constant rapid motion in all directions. During their motion, they keep on colliding with one another and. also with the walls of the container and, thus, change their directions.
- Molecular collisions are perfectly elastic, no loss of energy occurs when the molecules collide with one another or with the walls of the container. However, there may be. redistribution of energy during the collisions.
- There are no forces of interaction (attractive or repulsive) between molecules. They move completely independent of one another.
- The pressure exerted by the gas is due to the bombardment of its molecules on the walls of the container per unit area.
- The average kinetic energy of the gas molecules is directly proportional to the absolute temperature.
Question 3.
Explain the following observations.
(a) Aerated water bottles are kept underwater during summer.
Answer:
Aerated water contains CO2 gas dissolved in an aqueous solution under pressure and the bottles are well stoppered. As in summer temperature increases and we know that the solubility of the gases decreases with increase in temperature and as a result move of gas is expected to be generated may be large in quantity and hence pressure exerted by the gas may be very high and the bottle may explode. So, to decrease the temperature and hence to avoid explosion of the bottles.
(b) Liquid ammonia bottle is cooled before opening the seal.
Answer:
Liquid ammonia bottle contains the gas under very high pressure. If the bottle is opened as such, then the sudden decrease in pressure will lead to a large increase in the volume of the gas. As a result, the gas will come out of the bottle with force. This will lead to the breakage of the bottle. Cooling under tap water will result in a decrease in volume. It reduces the chances of an accident.
(c) The tyre of an automobile is inflated at lesser pressure in summer than in winter.
Answer:
The pressure of the air is directly proportional to the temperature. During summer due to high temperature, the pressure in the tyre will be high as compared to that in water. The tube may burst under high pressure in summer. Therefore, it is advisable to inflate the tyre to lesser pressure in summer than in winter.
(d) The size of the weather balloon becomes larger and larger as it ascends up to higher altitudes.
Answer:
Answered somewhere else in the book.
States of Matter Important Extra Questions Numerical Problems
Question 1.
In a hospital, an oxygen cylinder holds 10 L of oxygen at 200 atm pressure. If a patient breathes in 0.50 ml of oxygen at 1.0 atm with each breath, for how many breaths the cylinder will be sufficient. Assume that all the data is at 37°C.
Answer:
10 L at 200 atm =? L at 1 atm. [Temp, is constant at 37°C]
∴ Boyle’s law P1V1 = P2V2 can be applied
200 × 10 = 1 × V2
or
V2 = 2000 L
Number of breaths = \(\frac{\text { Total volume }}{\text { Volume inhaled per breath }}\)
= \(\frac{2000 \mathrm{~L}}{0.5 \times 10^{-3} \mathrm{~L}}\)
= 4 × 106
Question 2.
Calculate the pressure of 1 × 1022 molecules of oxygen gas when enclosed ¡n a vessel of 5-litre capacity at a temperature of 27°C.
Answer:
Number f moles of O2 = \(\frac{1 \times 10^{22}}{6.02 \times 10^{23}}\)
= 0.166 × 10-1 mol
= 1.66 × 102 mol
The pressure exerted by O2 molecules can be calculated by the equation
PV = nRT [Ideal gas equation]
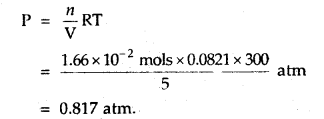
Question 3.
When a ship is sailing in the Pacific Ocean where the temperature is 23.4°C, a balloon is filled with 2 L air. What will be the volume of the balloon when the ship reaches the Indian Ocean, where the temperature is 26.1°C.
Answer:
V1 = 2 L
T1 = 23.4 + 273 = 296.4K
T2 = 26.1 + 273 = 299.1 K
From Charle’s Law
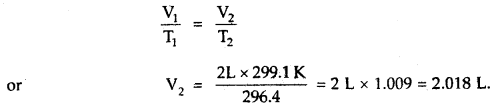
Question 4.
At what temperature centigrade, will the volume of a gas at 0°C double itself, pressure remaining constant?
Answer:
Let the volume of the gas at 0°C = V1 mL
Final Volume = V2 = 2V1 mL [Given]
T1 = OC + 273 = 273 K, T2 =?
Since Pressure remains constant
∴ Charles law can be applied
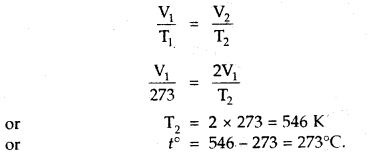
Question 5.
A bulb ‘B’ of the unknown volume containing gas at one atmospheric pressure is connected to an evacuated bulb of 0.5-litre capacity through a stop-cock. On opening the stop-cock, the final pressure was found to be 570 mm at the same temperature. ‘What is the volume of bulb ‘B’?
Answer:
Let the volume of the bulb = V1; P, = 1 atm
Evacuated Bulb has volume = 0.5 L;
Total volume of both bulbs after the opening of stop-cock = (V1 + 0.5) L i.e. V2 = (V1 + 0.5):
P2 = 570 mm = \(\frac{570}{760}\) atm
Apply Boyle’s law P1V1 = P2V2
1 × V1 = \(\frac{570}{760}\) × (V1 + 0.5)
On solving the above equation
V1 = 1.5 L
∴ Volume of the unknown bulb ‘B’ = 1.5 L
Question 6.
1 mole of SO2 occupies 1.5 L at 25°C. Calculate the pressure exerted by gas assuming that gas does not obey the ideal gas equation. (Given a = 3.6 atm L2mol-2, b = 0.04 L mol-1) where a, b are van der Waal’s constants.
Answer:
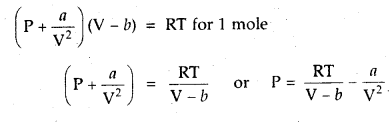
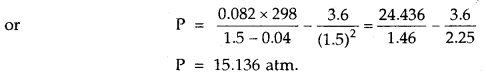
Question 7.
A gas occupies a volume of 2.5 L at 9 × 105 Nm-2. Calculate the additional pressure required to decrease the volume of the gas to 1.5 L, keeping the temperature constant.
Answer:
V1 = 2.5 L; P1 = 9 × 105 Nm-2
V2 = 1.5 L; P2 =?
Since temperature is constant, Boyle’s law is applied.
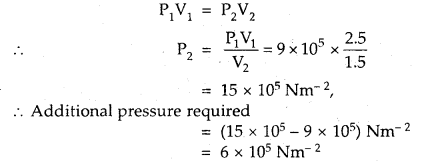
Question 8.
What volume of air will be expelled from a vessel containing 400 cm3 at 7° C when it is heated to 27° C at the same pressure?
Answer:
As the pressure is constant, Charles law is applied
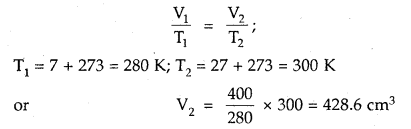
428.6 cm3 is the volume after expansion
∴ Volume expelled = (428.6 – 400) cm3 = 28.6 cm3.
Question 9.
A 10.0 L container is filled with a gas to a pressure of 2.0 atm at 0°C. At what temperature will the pressure of the gas inside the container be 2.50 atm.
Answer:
As the volume of the container remains constant, Gay- Lussac’s Law/Amonton’s Law is applicable
\(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\)
\(\frac{2}{273}=\frac{2.50}{\mathrm{~T}_{2}}\)
T2 = 341 K
or
t2 = (341 – 273)°C = 68°C.
Question 10.
One litre flask containing vapours of methyl alcohol (Mol. mass = 32) at a pressure of 1 atm and 25°C was evacuated till the final pressure was 10-3 mm. How many molecules of methyl alcohol were left in the flask?
Answer:
P1 = 10-3 mm; V1 = 1000 cm3; T1 = 298 K
Converting this volume to volume, at STP, where T2 = 2/3 K and P2 = 760 mm
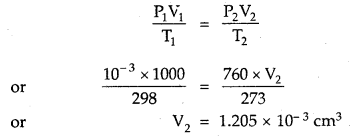
Now, 22400 cm3 at STP contains 6.02 × 1023 molecules
∴ 1.205 × 10-3 cm3 at STP contains
= \(\frac{6.02 \times 10^{23}}{22400}\) × 1.205 × 10-3 molecules
= 3.24 × 1016 molecules.
Question 11.
A sealed tube that can withstand a pressure of 3 atm is filled with air at 27°C and 760 mm pressure. Find the temperature above which it will burst?
Answer:
Applying gas equation \(\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\) as volume of the sealed tube remains constant .
\(\frac{1}{300}=\frac{3}{\mathrm{~T}_{2}}\)
T2 = 900 K
or
t2 = 900 – 273 = 627°C.
Question 12.
The temperature at the foot of a mountain is 30°C and pressure is 760 mm. Whereas at the top of the mountain these are 0°C and 710 mm. Compare the densities of the air at the foot and at the top.
Answer:
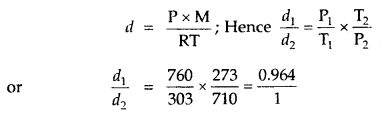
∴ the ratio of densities of air at the foot and the top of the mountain = 0.964: 1.
Question 13.
10.0 g of O2 were introduced into an evacuated vessel of 5-litre capacity maintained at 27°C. Calculate the pressure of the gas in the atmosphere in the container.
Answer:
Volume of the gas = V = 5 L;
Wt. of O2 = 10.0 g
Molar mass of O2 = 32.0
∴ No. of moles = \(\frac{10}{32}\)
T = 27 + 273 = 300 K; R = 0.0821 L atm K-1 mol-1
From ideal gas equation,
PV = nRT, we get
P = \(\frac{10}{32}\) × 0.0821 × 300 = 1.54 atm.
Question 14.
8.0 g of methane is placed in a 5 L container at 27°C. Find Boyle constant.
Answer:
Pressure × Volume is called Boyle’s constant
PV = nRT = \(\frac{W}{M}\) RT ,
= \(\frac{8}{16}\) × 0.0821 × 300
= 12.315 L atm
Question 15.
The density of A gas is 3.80 g L-1 at STP. Calculate its density at 27°C and 700 torr pressure
Answer:
d = \(\frac{PM}{RT}\)
For the same gas at two different pressures and temperatures,
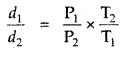
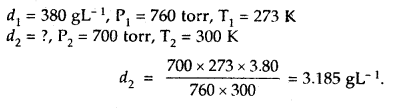
Question 16.
If the density of a gas at sea level and 0°C is 1.29 kg m-3, what will be its molar mass (Assume that pressure is equal to 1 bar).
Answer:
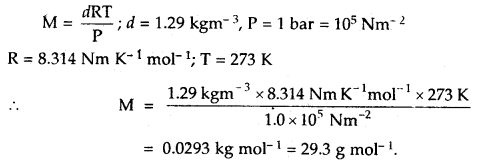
Question 17.
A gaseous mixture contains 56 g N2, 44 g CO2 and 16 g CH4 The total pressure of the mixture is 720 mm Hg. What is the partial pressure of CH4?
Answer:
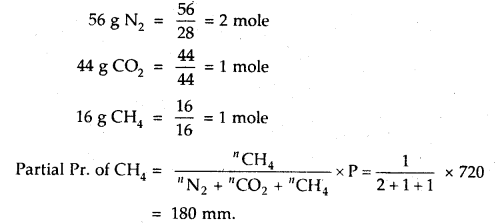
Question 18.
A 2 L flask contains 1.6 g of methane and 0.5 g of hydrogen at 27°C. Calculate the partial pressure of each gas in the mixture and hence calculate the total pressure.
Answer:
1.6 g CH4 = \(\frac{1.6}{16}\) = 0.1 Mole
16
Partial pressure of CH4 (pCH4) = CH4 × \(\frac{RT}{P}\)

Question 19.
One mole of S02 gas occupied a volume of 350 mL at 27°C and 50 atm pressure. Calculate the compressibility factor of the gas. Comment on the type of deviation shown by the gas from ideal behaviour.
Answer:
Compressibility factor, Z =
Here n = 1, P = 50 atm, V = 350 × 10-3 L = 0.35 L
R = 0.0821 L atm K-1 mol-1; T = 27 + 273 = 300 K
∴ Z = \(\frac{50 \times 0.35}{1 \times 0.0821 \times 300}\) = 0.711
For an ideal gas Z = 1
As for the given gas Z < 1, it shows a negative deviation, i.e., it is more compressible than expected from ideal behaviour.
Question 20.
A mixture of CO and CO2 is found to have a density of 1.5 g L-1 at 20°C and 740 mm pressure. Calculate the composition of the mixture.
Answer:
1. Calculation of average molecular mass of the mixture
M = \(\frac{d R T}{P}=\frac{1.50 \times 0.0821 \times 293}{\frac{740}{760}}\) = 37.06
2. Calculation of percentage composition
Let mol% of CO in the mixture = x
Then mol% of CO? in the mixture = 100 – x
Average molecular mass
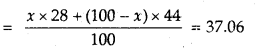
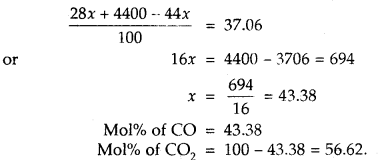
Question 21.
A 5-L vessel contains 14 g of nitrogen. When heated to 1800 K, 30% of molecules are dissociated into atoms. Calculate the pressure of the gas at 1800 K.
Answer:
N2 ⇌ 2N
Initial moles = \(\frac{1.4}{28}\) = 0.05
Moles left = 0.05 – \(\frac{30}{100}\) × 0.05 = 2 × 0.015 = 0.03
∴ Total no. of moles = 0.035 + 0.030 = 0.065
i.e. n = 0.065 mol, V = 5 L, T = 1800 K; P =?
P = \(\frac{n \mathrm{RT}}{\mathrm{V}}=\frac{0.065 \times 0.0821 \times 1800}{5}\)
= 1.92 atm.
Question 22.
Calculate the temperature of 2 moles of S02 gas contained in a 5 L vessel at 10 bar pressure. Given that for SO2 gas van der Waal’s constant is a – 6.7 bar L2 mol-2 and b = 0.0564 L mol-1.
Answer:
According to van der Waal’s equation
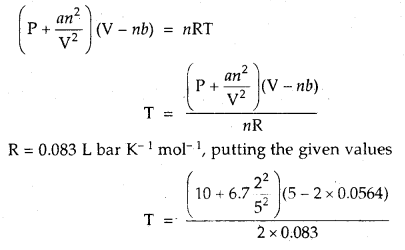
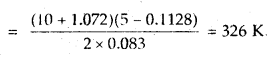
Question 23.
A given mass of a gas occupies 919.0 mL in a dry state at STP. The same mass when collected over water at 15°C and 750 mm pressure occupies on litre volume. Calculate the vapour pressure of water at 15°C.
Answer:
If p is the vapour pressure of water at 15°C, then P2 = 750 – p
From the gas equation \(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\), we get
\(\frac{760 \times 919}{273}=\frac{(750-p) \times 1000}{288}\)
or
p = 13.3 mm
∴ Vapour pr. of water = 13.3 mm.
Question 24.
A steel tank containing air at 15 atm pressure at 15°C ¡s provided with a safety valve that will yield at a pressure of 30 atm. To what minimum temperature must the air be heated to below the safety valve?
Answer:
\(\frac{P_{1}}{P_{2}}=\frac{T_{1}}{T_{2}}\)
i.e., \(\frac{15}{30}=\frac{288}{\mathrm{~T}_{2}}\)
or
T2 = 576 K
or
t2°C = 576 – 273 = 303°C
Question 25.
Calculate the pressure exerted by 110 g of CO2 in a vessel of 2 L capacity at 37°C. Given that the van der Waals constants are a = 3.59 L2 atm mol-2 and b = 0.0427 L mol-1. Compare the value with the calculated value if the gas were considered ideal.
Answer:
According to van der Waals equation
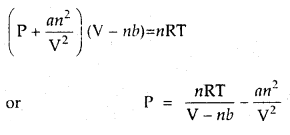
110
Here, n = \(\frac{110}{44}\) = 2.5 moles. Putting the given values, we get
P = \(\frac{2.5 \times 0.0821 \times 310}{(2-2.5 \times 0.0427)}-\frac{3.59 \times 2.5}{2}\)
= 33.61 atm – 5.61 atm = 28.0 atm
If the gas were considered an ideal gas. applying ideal gas equation
PV = nRT
or
P = \(\frac{n \mathrm{RT}}{\mathrm{V}}\)
∴ P = \(\frac{2.5 \times 0.0821 \times 310}{2}\) = 31.8 atm